射影几何中对合问题的研究
晋 珺
(晋中学院数学学院,山西晋中030619)
1 维射影变换
1.1 定义
定义1.1两个重叠的一维基本形的射影对应叫做一维射影变换.[1]4
1.2 代数表示
定理1.1两个点列间射应变换的代数表达式为非奇线性对应,
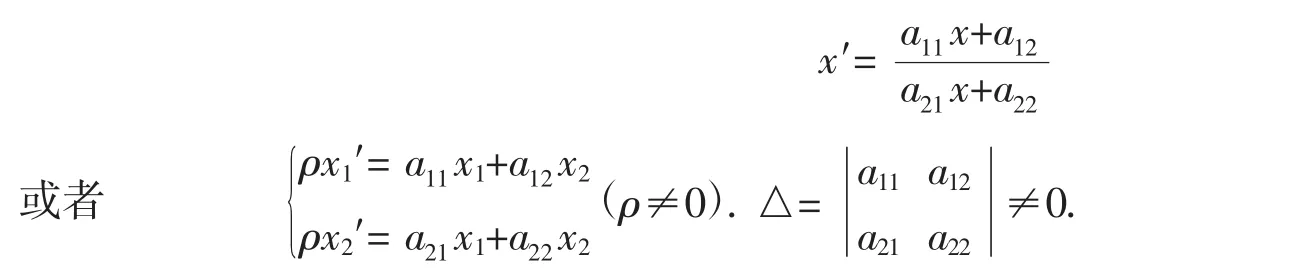
1.3 对应点参数满足的方程
定理1.2两个重叠的一维基本形A+λB,A+λ′B间的射影变换对应点参数满足的条件为
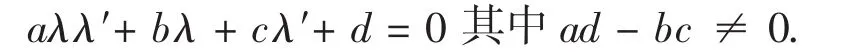
1.4 决定的条件
定理1.3已知三对对应元素则可以唯一决定一个射影变换.(因为三对对应元素就可以确定a:b:c:d,决定了这个变换)
1.5 二重元素(自对应元素)
两个不同实的自对应元素,称为双曲型的射影变换.
两个相同实的自对应元素,称为抛物型的射影变换.
一对共轭虚的自对应元素,称为椭圆型的射影变换.
2 对合
2.1 定义
定义2.1在一维射影变换中,如果对于任何元素,无论看作第一基本形还是第二基本形,它的对应元素是一样的,那么这种非恒等的射影变换叫做对合.[2]11
2.2 代数表示
定理2.1对合的代数表达式为
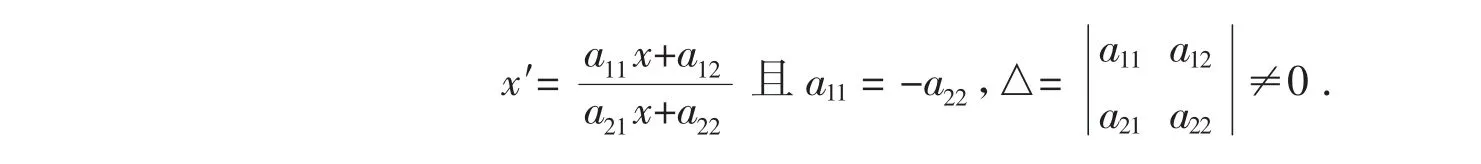
证明:射影变换为对合两式相减得且a11=-a22.
2.3 对应点参数满足的方程
定理2.2两个重叠的一维基本形A+λB,A+λ′B成为对合的充要条件是对应点的参数λ与λ′满足以下方程:
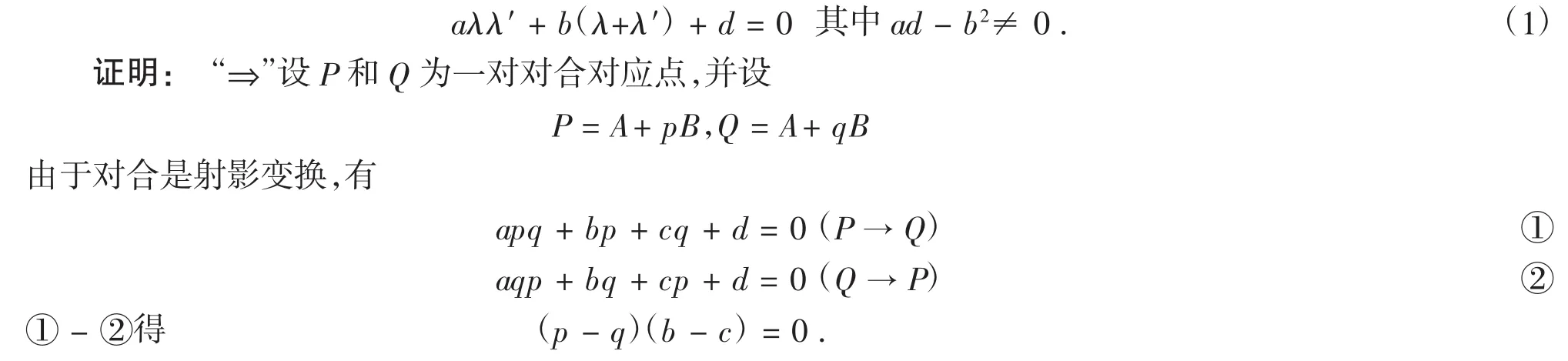
由于P和Q是不同点,所以p≠q.

因此,对合的对应点参数满足
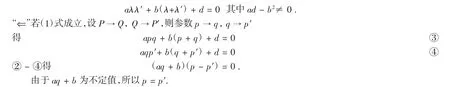
所以P→Q,Q→P,此时射影变换为对合.
2.4 决定的条件
定理2.3已知两对对应元素则可以唯一决定一个对合.
证明:由于对合对应点参数满足方程:

可以求得a:b:d确定对合方程.
2.5 二重元素(自对应元素)
两个不同实的自对应元素,称为双曲型的对合.
一对共轭虚的自对应元素,称为椭圆型的对合.
注:在对合方程
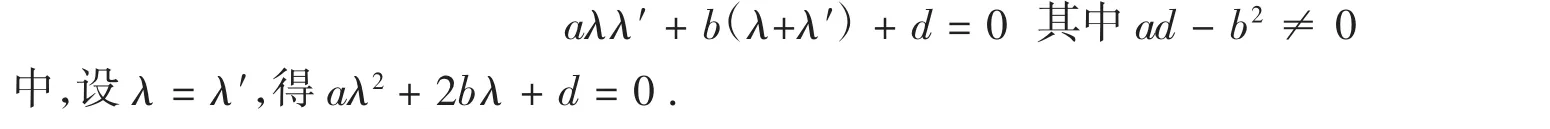
由于△=4b2-4ab≠0,所以△>0时,两个不同实的自对应元素称为双曲型的对合;△<0时,一对共轭虚的自对应元素称为椭圆型的对合.△≠0,无抛物型的对合.
2.6 双曲型对合的一个性质
定理2.4双曲型对合的任何一对对应元素p-p′,与其两个二重元素E,F调和共轭,即

3 对合相关题型求解
例 1求对合的自对应点坐标 .[3]
解:1)首先排除自对应点为无穷远点,因为(1,0)→(1,0)时,必有a21=0,此题a21=4≠ 0.
2)将对合表达式化为非齐次坐标形式

化为齐次形式,自对应点为(1,1)(-1,2).
例2已知对合的两对对应元素参数为3→2,5→1,试求此对合方程,并求二重元素.
解:将3→ 2,5→ 1代入
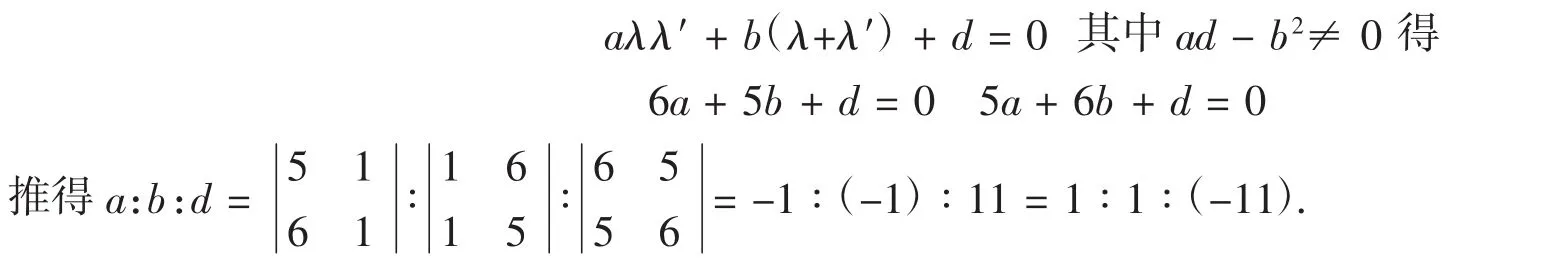
所以此对合方程为


