基于马氏距离的样品判别评价研究
张国俭
(晋中学院数学学院,山西晋中030619)
判别分析是一种应用十分广泛的统计分析方法,在经济学、地质学、医学、气象学等学科中均有广泛的应用.判别分析的方法主要有距离判别、贝叶斯判别、费歇判别、逐步判别、非参数判别等[1~3],对判别准则的评价方法有回代估计法、交叉确认估计法[1](刀切法[4])、前瞻性考核[4]等.总体而言,它们只研究了判别方法及对判别准则的评价,而没有对一个固定的样品其判别优劣评价的研究,而现实中这样的评价又具有重要的意义.有鉴于此,本文首先对两个正态总体的样品判别优劣的评价进行了研究,然后又推广到多个正态总体,提出了待判域的概念,用以鉴别距离差没有统计学意义的样品,在此基础上,提出了判别系数的概念,用以对样品判别的优劣进行评价.最后,指出了本文的不足之处以及需要进一步研究的方面.
1 准备知识
定理1.1[1]设G1和G2是两个不同的p维已知总体,其均值向量分别为μ1和μ2,协方差矩阵相等且都为Σ,x0为一样品值,记W(ix0)=+bi,ai=Σ-1μi,bi=Σ-1μi,i=1,2.则判别准则为:
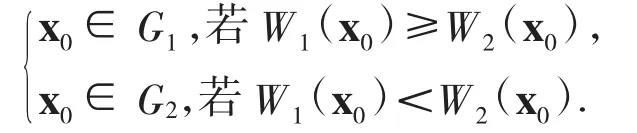
定理 1.2[1]设 G1,G2,…,Gk是 k 个不同的 p 维已知总体,其均值向量分别为 μ1,μ2,…,μk,协方差矩阵相等且都为Σ,x0为一样品值,记W(ix0)=+bi,ai=Σ-1μi,bi=μi,i=1,2,…,k.则判别准则为:
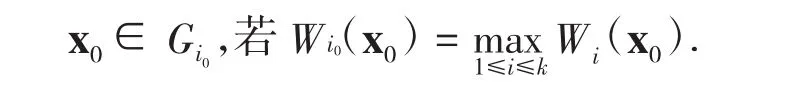
对于x是p维随机向量,有如下的结论:
定理1.3[1]设x~Np(μ,Σ),又Y=ATx+b,其中b为p维常向量,AT是l×p矩阵,rank(AT)=l,则Y~Nl(ATμ+b,ATΣA).
定理1.4若x~N(μ,Σ),则Wi(x)~N(+bi,Σai),i=1,2,…,k.
证明:x是来自p维正态总体的任一样品,由定理1.3知,随机变量Wi(x)服从正态分布.下面求Wi(x)的数学期望与方差:
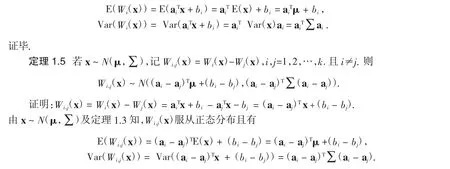
证毕.
注:这里为了整篇文章的符号统一,上面有些定理中的符号做了适当的修改,只是所用的符号不同,不会影响整个定理的正确性.
2 显著性检验
大家只对判别准则的评价进行了研究,对于一个固定的样品,并没有对其判别评价的研究,而现实中后者又有重要的意义.比如,有某种疾病,样本分为患病和不患病两类.在马氏距离判别准则下,如果某样品的数据指标离两个总体的距离相等,就无法对其进行判别,即使把其归为其中的一类,其实际意义也不大.同理,如果其数据指标虽然不等,但很接近,其实际意义也不大.如果此样品为患者,说明此样品刚患病,其数据指标不明显.如果此样品不是患者,说明此样品患病的趋势已经很明显,稍不加注意就可能患病,应该进行药物控制或多加强锻炼.所以,患病和不患病中间还有一个比较模糊的区域.下面对样品的判别函数的差异进行显著性检验,提出了待判域的概念,用以对数据指标没有明显所属的样品进行鉴别,同时提出了判别系数的概念,用以对样品的判别优劣进行评价.
对一个固定的样品来说,不同的观测有不同的观测向量,所以可以把它看作一个随机向量.设样品x=(x1,x2,…,xp)T是p维空间中的一个随机向量,由于它取自协方差阵皆为Σ的正态总体中的一个,故可设x~Np(μ,Σ)(μ未知).而具体的数据向量x0=(x10,x20,…,xp0)T看成x的一个观测向量,下面对判别函数的差异做显著性假设检验.
2. 1 两个正态总体的情形
设G1和G2是两个不同的p维正态总体,其均值向量分别为μ1和μ2,协方差矩阵相等且都为Σ.由定理1.1可以确定判别函数Wi(x),i=1,2.
由定理1.4知,Wi(x)~N(+bi,Σai),i=1,2.不妨设W1(x0)>W2(x0),下面对E(W1(x))>E(W2(x))做显著性检验:
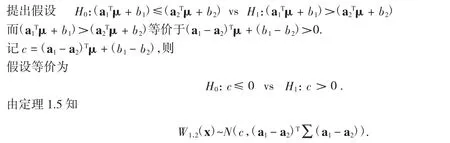
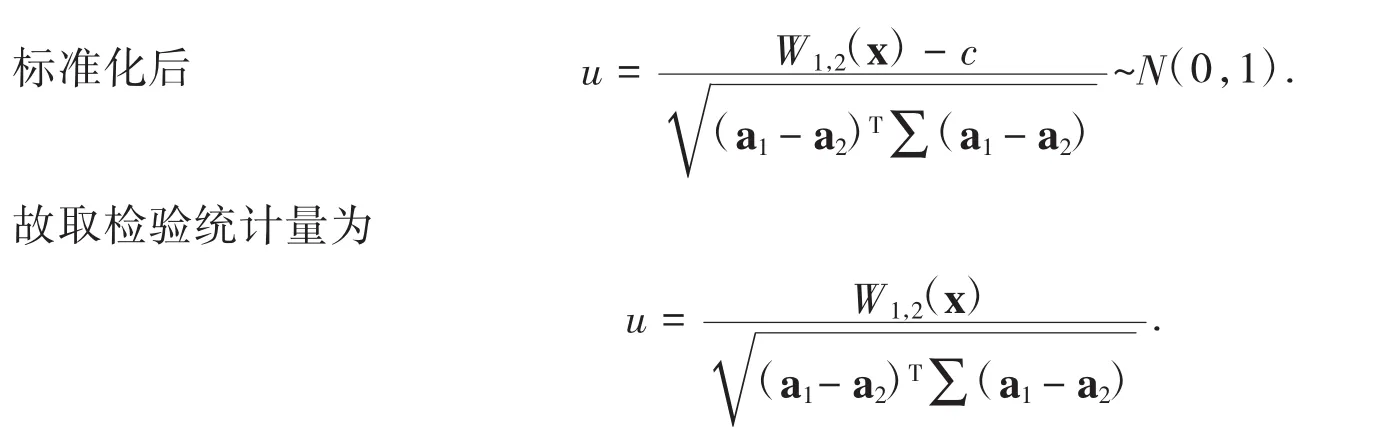
拒绝域 {u≥u1-α}[5],其中 u1-α为标准正态分布的 1-α 分位数.

定义2.1把上面的保留域{u<u1-α}称为判别分析中样品x0的待判域.
由定义2.1知道,如果x0落入待判域,说明样品x0离两个总体的马氏平方距离差没有统计学意义.可以把x作为待观察的对象.
检验的p值为:p=1-Φ(u0),其中u0是由x0算出的u值.
由p值的意思可知,p值越小,越拒绝原假设,判别越好.
定义2.2把R=1-p=Φ(u0)称为样品x0的判别系数.
由定义2.2知道,0<R<1,且R越接近1,判别越好.而R越接近0,判别越差.一般情况下,判别可以接受时,应有R≥0.9.
2.2 k个不同的p维正态总体的情形
设 G1,G2,…,Gk是 k 个不同的 p 维正态总体,其均值向量分别为 μ1,μ2,…μk,协方差矩阵相等且都为Σ,由定理1.2知,判别准则为x0∈,若x0)=W(ix0).
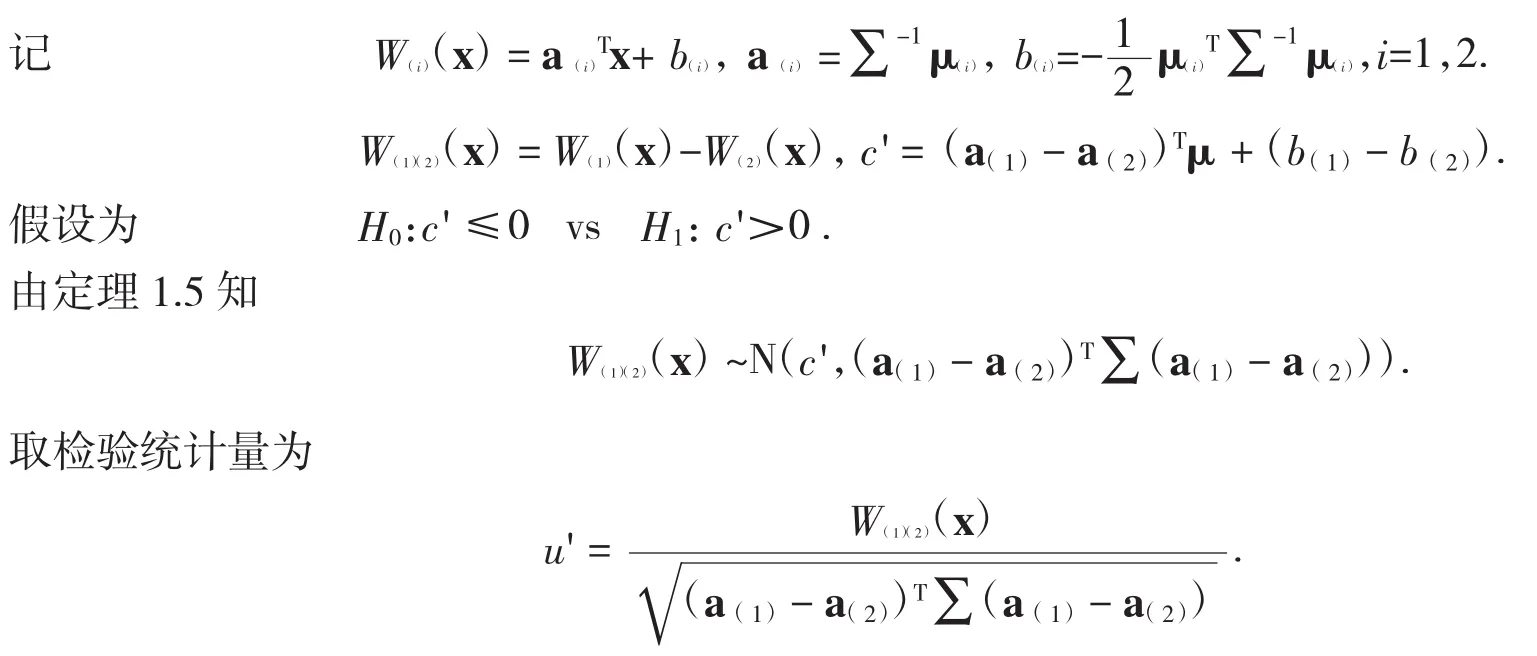
拒绝域 {u'≥u1-α}.
若{u'<u1-α}成立,则E(W(1)(x))>(W(2)(x))没有统计学意义,说明x到总体(1)和到总体(2)的马氏平方距离差没有统计学差别,x可以被判属于总体(1),也可以被判属于总体(2),甚至还可以被判属于其他总体.这时,我们说x是待判的.即待判域为{u'<uα}.
否则,E(W(1)(x))>E(W(2)(x))有统计学意义.就可以说,x到(1)这个总体的距离最小.判x属于总体(1).
判别系数为:R=Φ(u0'),其中,u0'是由x0算出的u'值.
3 本文的不足之处及需要改进的地方
1)本文只研究了总体为正态总体的情形,对于非正态总体的情况没有研究;
2)本文只研究了协方差阵相等的情形,对于协方差阵不等的情形没有研究;
3)文章只研究了正态总体参数已知的情形,总体的参数未知时没有研究;
4)对样品的评价除了待判域和判别系数外还应该考虑判别函数整体的评价,最好做个综合指标;
5)本文没有做实证研究,还需要做实证以检验判别的误判率的改进程度.

