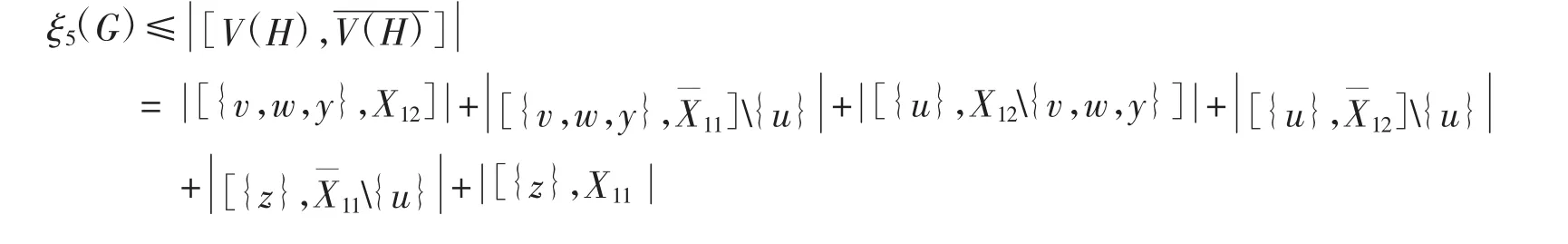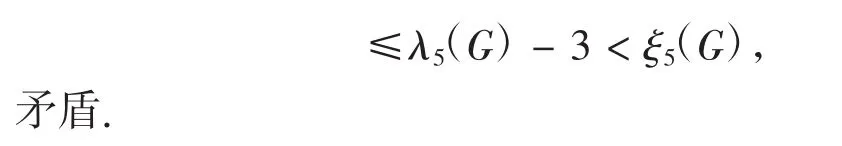二部图是极大5限制边连通的充分条件

张 磊，张国志

（晋中学院数学学院，山西晋中030619）

0 引言

多处理机的互连网络拓扑通常以图为数学模型，其中图的顶点代表处理机，边代表处理机之间的直接通信联系，故网络拓扑的性能可以通过图的性能和参数来衡量.为系统设计或者选择网络拓扑时，一个基本的考虑是系统的可靠性，它对应的连通性.但是用边连通度来研究系统的可靠性不够精确.在此背景下，1996年Fabrega和Foil［1］提出了k限制边连通度的概念提出了限制边连通度的概念.近年来，对于一般的正整数k，k限制边连通度得到了广泛的研究见文［2～4］.

1 准备工作

在文中，我们主要考虑无向简单图.文中未给出的概念和符号见文［5］.设G是一个连通图.用υ=表示G的阶.若e=u，υ是G一条边，则称u与υ相邻.设S为G中的一个边集，对于G中任意一点u，用N（u）表示在G中与u的邻点的集合，用d（u）=表示在G中与u相邻的点的个数.设W=υ0υ1υ2…υk是图G的一条路.此时，若υ0=υk，则称W为G中的圈.W中边的数目称为W的长.长为k的路（或圈）称为k-路（或k-圈）.G的围长g（G）是指G中最短圈的长.在G中顶点u和υ之间的距离d（u，υ）是最短（u，υ）-路的长.U，T 是 V（G）的非空子集，定义 d（U，T）=min｛d（u，υ）∶u∈U，υ∈T｝为 U，T 之间的距离.所谓二部图是指一个图，它的顶点集可以划分为两个非空子集V1和V2，使得任意的e=u，υ∈E（G）满足=1；（V1，V2）称为 G 的二分类.

定义 1.1对于具有二分类（V1，V2）的二部图 G 中的两个点集 U，T，令 Ui=U∩Vi，Ti=T∩Vi其中 i=1，2.称满足 d（U1，T1）=d（U2，T2）=k 的点集（U，T）对是（k，k）-距离极大的，如果不存在 U⊆U′，T⊆T′满足 U≠U′或 T≠T′，使得 d（U′1，T′1）=d（U′2，T′2）=k.

1996年，为了精确研究并行计算机系统互连网络拓扑的可靠性，Fàbrega和Foil［1］推广了边连通度λ（G），提出了k限制边连通度 λ（kG）.

定义1.2［1］设G图是连通图，S⊆E（G）是G的边割.如果G-S至少包含两个连通分支且对于G-S的任意分支H都有V（H）≥k，那么称满足这样条件的边数最少的边割为G的λk-割，G中所有λk-割所含边数的下界称为G的k限制边连通度λ（kG）.

目前，k限制边连通度得到了学者们的高度关注［2～4］.从现有研究成果来看，连通图G的λ（kG）越大，G所对应的网络拓扑的性能越高［6，7］.对正整数k，定义 ξ（kG）=min｛=k，G［X］连通，=V（G）X｝.如果λ（kG）=ξ（kG），那么称G是极大k限制边连通图.

本文将给出二部图中存在极大（4，4）-距离点集对与λ（5G）的关系.

2 主要结论

我们先给出以下将要用到的引理.

引理2.1［8］设G是λk-连通图.当k≥5时，如果υ＞k（k-1），则λk（G）≤ξk（G）.

引理2.2［9］令G是一个满足λk（G）≤ξk（G）的λk-连通图且［X，Y］是G的一个λk-割.若G［X］中存在一个k阶连通子图H满足

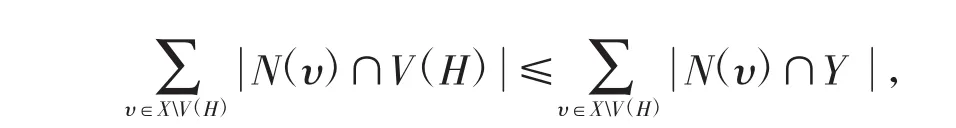
则G是极大k限制边连通的.

定理2.1设G是一个阶υ＞20且δ（G）≥2的λ5-连通二部图.若G的围长g＞6且对于G中任意的（4，4）-距离极大点集对（U′，T′），在 G（U′∪T′）中存在同构于 K1，4的连通分支，则 G 是极大 5 限制边连通的.

证明用反证法.由引理2.1知，λ（5G）≤ξ（5G）.假设G不是极大5限制边连通的.则 λ（5G）＜ ξ（5G）.设（V1，V2）为 G 的一个二分类矛盾.故

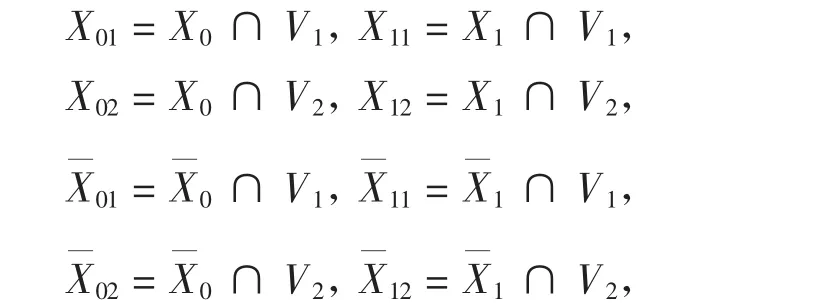
断言X01≠Ø 且X02≠Ø.

用反证法.假设X01=Ø或X02=Ø.由于G［X］连通且X ≥6，因此G［X］中存在5阶连通子图H0.因为g ＞ 6，所以对任意 x∈X1≥V（H0）有

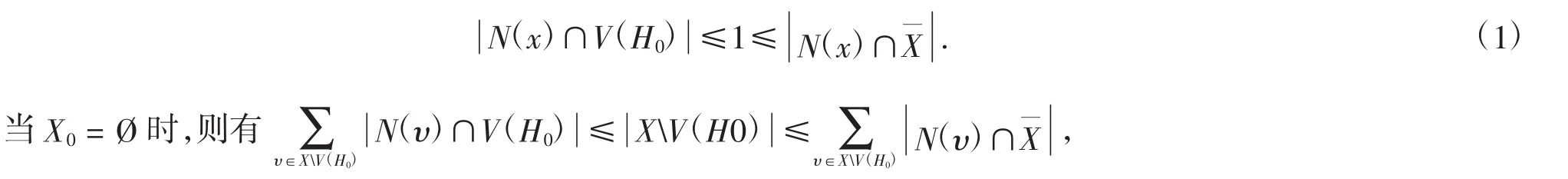
由引理2.2知，G是极大5限制边连通的，矛盾.

因此X0≠Ø.注意到X01=Ø或X02=Ø.不妨设假设X01=Ø.则X02≠Ø，即X=X11∪X02∪ X12.因为g＞6，所以H0为树.因为H0连通，所以

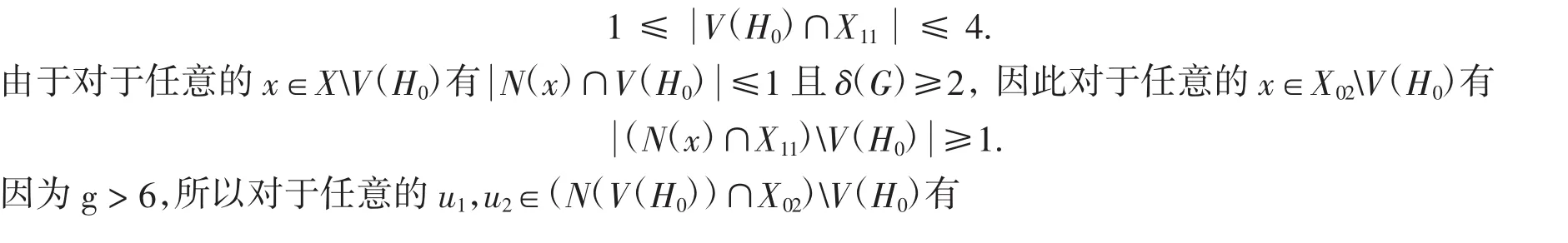
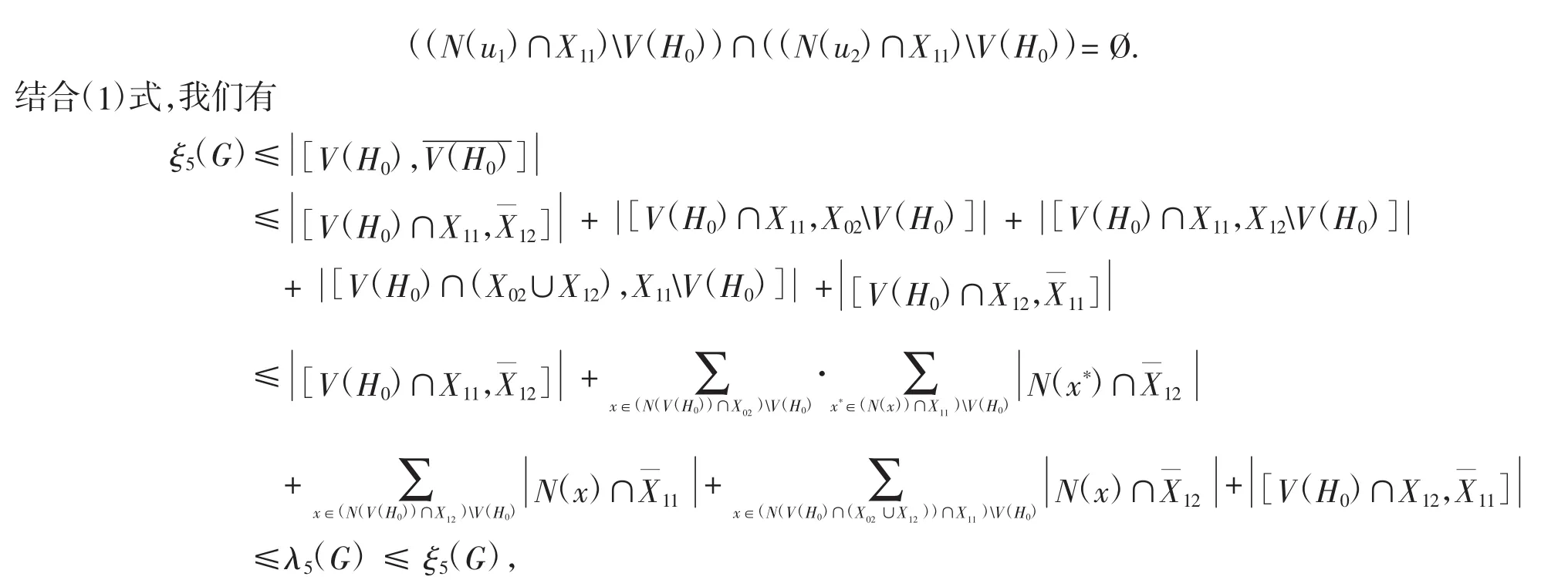
矛盾.断言证明完成.

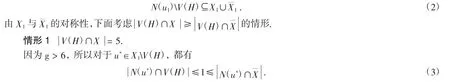
结合（2）式和H是G［U∪T］中的连通分支，可知对于任意一点u′∈X0V（H），都有

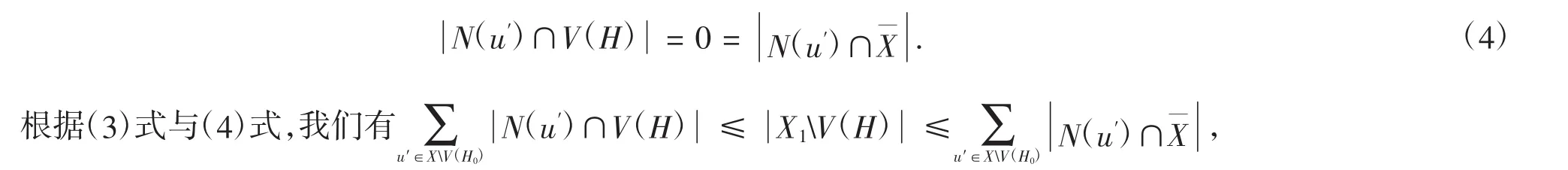
由引理2.2知，G是极大5限制边连通的，矛盾.

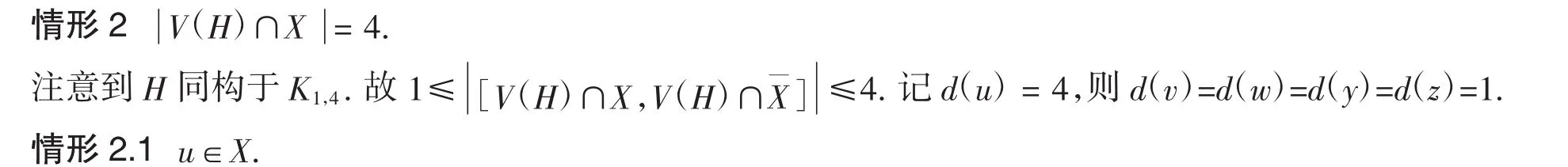
矛盾.

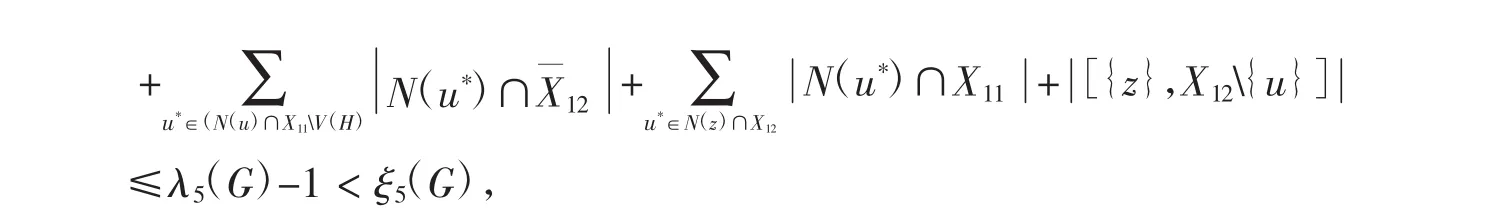
情形2.2u∉X.

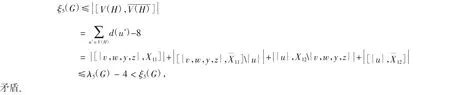
情形3V（H）∩X=3.

注意到 H 同构于 K1，4.故 2≤V（H）∩X，V（H）∩］≤3.记 d（u）=4，则 d（v）=d（w）=d（y）=d（z）=1.

情形3.1u∈X.

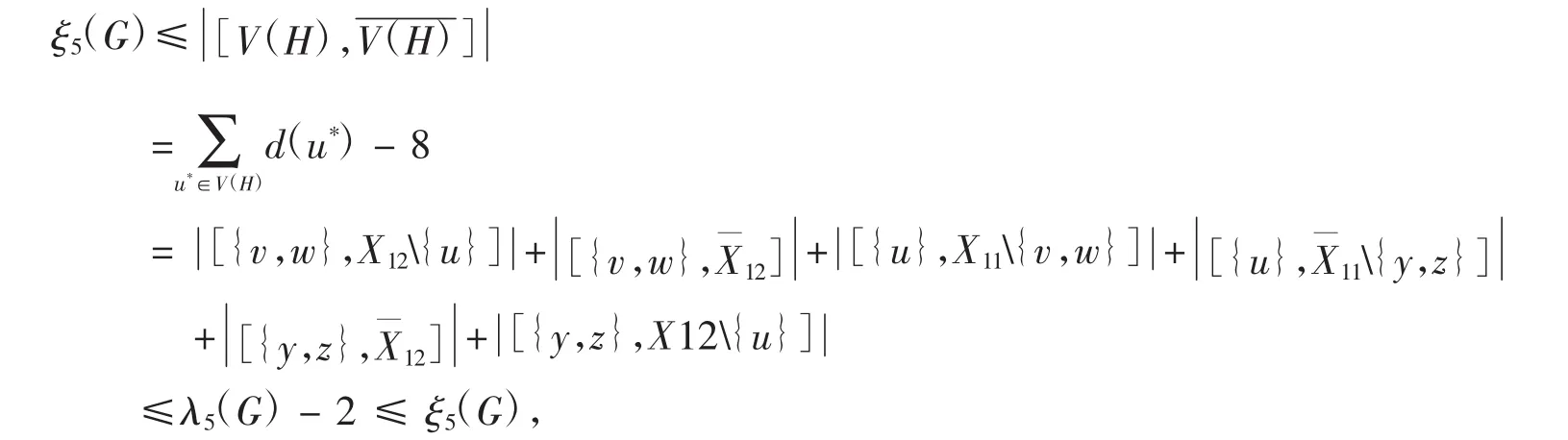
矛盾.

情形3.2u∉X.