山西省2018年中考数学22题的多维思考

冀怀忠

（和顺县教师进修学校，山西和顺032700）

山西省2018年中考数学22题系初中数学“图形与几何”范畴的“综合与实践”题目.试题遵循《课程标准》之要求，立足基础，不偏不难，体现了数学探究活动过程，彰显了对学生数学核心素养的考查，利于学生数学思维能力的发展，值得思考和研究.

1 试题呈现（山西中考数学22题——综合与实践）

1.1 问题情境

在数学活动课上，老师出示了这样一个问题：如图1，在矩形ABCD中，AD=2AB，E是AB延长线上一点，且BE=AB，连接DE，交BC于点M，以DE为一边在DE的左下方作正方形DEFG，连接AM.试判断线段AM与DE的位置关系.

1.2 探究展示

勤奋小组发现，AM垂直平分DE，并展示了如下的证明方法：

证明：∵BE=AB，∴AE=2AB.

∵ AD=2AB，∴ AD=AE，

∵四边形ABCD是矩形，∴AD∥BC.

即AM是△ADE的DE边上的中线.

又∵ AD=AE，∴ AM⊥DE，（依据2）

∴AM垂直平分DE.

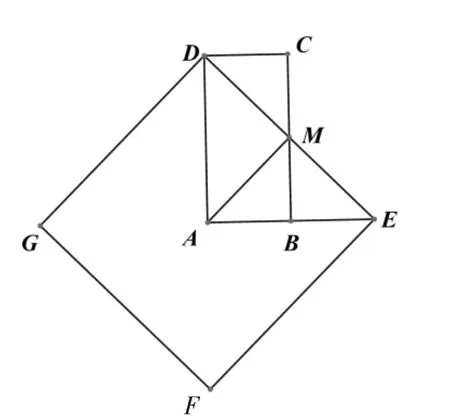
图1

1.3 反思交流

1）上述证明过程中的“依据1”“依据2”分别是指什么？试判断图1中的点A是否在线段GF的垂直平分线上，请直接回答，不必证明.

2）创新小组受到勤奋小组的启发，继续进行探究，如图2，连接CE，以CE为一边在CE的左下方作正方形CEFG，发现点G在线段BC的垂直平分线上，请你给出证明.

1.4 探索发现

如图3，连接CE，以CE为一边在CE的右上方作正方形CEFG，可以发现点C和点B都在线段AE的垂直平分线上，除此之外，请观察矩形ABCD和正方形CEFG的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明.

图2

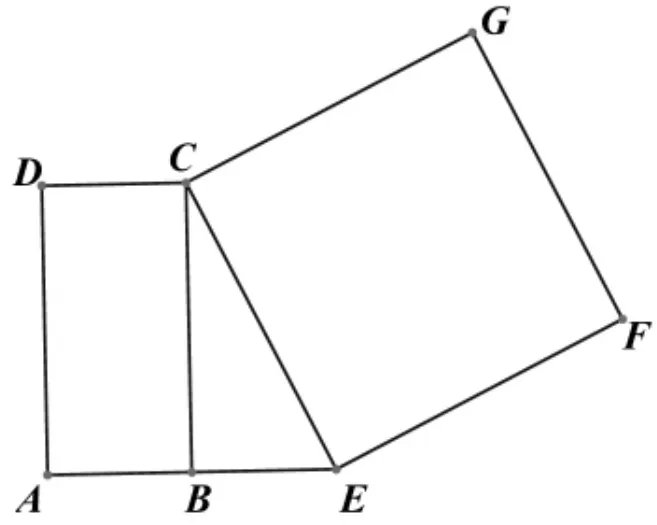
图3

2 试题思考

试题突出数学核心素养，关注探究实践活动经历，对数学教学具有很好的导向作用.

2.1 探究活动的范例

试题结构包括有“问题情境”“探究展示”“反思交流”“探索发现”四部分，其以矩形为载体，构造直角三角形、正方形等情境，围绕有关“点在线段的垂直平分线”问题展开探究活动.“问题情境”先是对特殊矩形进行图形延展，出现直角三角形和正方形，要求判断图中两线段的位置关系.“探究展示”环节为学生探究、讨论后出示的一种解答方案.“反思交流”首先体现良好的思维习惯，对上面某小组展示的解答过程寻找推理依据，并联想、提出“点A是否在线段GF的垂直平分线上”的相关问题，接着给出创新小组受如前探究活动“启发”的类比联想，重新构建直角三角形、正方形新情形如图3，猜想、发现具有类似“点在线段垂直平分线上”的结论.“探索发现”，在前一环节的基础上又产生联想，对称性地变化所构正方形“CE为一边在CE的右上方作正方形”，类比性的正常思维提出，是否又存在“点在线段垂直平分线上的特征”猜测等.

试题的几个环节具有一定的关联性.以“点在线段垂直平分线上”为主线，进行逻辑性的、环环相扣的类比，产生一系列的猜想，并给予推理论证.一定意义上讲，这一过程是人们科学认识世界的浓缩过程，是人们获得新知的有效途径和方法.学生经历、体现如此过程的训练，有助于形成正确的思维方式，培养学生逻辑思考问题的良好思维习惯；有助于学生发现问题、提出问题、分析问题和解决问题能力的培养，发展学生的逻辑思维能力；有助于学生获得新知探究过程的体验和感悟，彰显出“综合与实践活动”对学生基础知识、基本能力以及数学思维的综合训练之特点.笔者认为，该题目设置的结构模式展现了科学的思维过程，充满了探究的意味，具有探究实践活动范例之功效，对教学活动的实施有良好的导向作用.

2.2 核心素养的考查

一般地，初中数学核心素养包括数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识等.在对学生数学核心素养考查方面，该试题显得尤为突出，重点地考查了学生的推理能力、空间观念、几何直观、创新意识等.

首先，试题具有综合性的特点.试题要求学生认真阅读题干，从中获取信息，经历操作、猜想、推理证明等过程.第（1）问依据的寻找，强化了数学推理须逻辑严谨、有理有据的观点.各个环节相继提出的问题需要一定合情推理能力作保障.对所给结论或猜想的证明，考查了学生的推理能力.试题中图形的变化，隐含了空间观念的考察.“问题情境”中，两线段位置关系的判断，“探索发现”环节的“请写出一个你发现的结论”等，需要学生具有一定的“几何直观”素养和猜想、推理能力.第（3）问题的分析，对于矩形ABCD和正方形CEFG，除题设所给“发现点C和点B都在线段AE的垂直平分线上”不需要考虑外，涉及到的顶点还有点A、D、E、F、G.几何直观，观察发现，所给矩形、正方形某边垂直平分线上的顶点只可能有A、F两个顶点，其他的点D、点E、点G一定是不行的.接着可判断点A也是不具备条件的，事实上，如图4，若顶点A具备，只可能是CE或FG的垂直平分线上的点，过点A作CE的垂线AH，垂足为H，连接AC，因在Rt△ACH和Rt△AEH中，显然AC≠AE，根据勾股定理，CH≠EH，故点A非CE垂直平分线上的点，也非FG垂直平分线上的点.故猜想到的结论可能是“点F是CB垂直平分线上的点”，后经推理论证，该结论得到证明.几何直观把复杂的数学问题变得简单、形象，获得了很多有效判断.凡此种种均考察了学生数学核心素养.

其次，试题体现出探究、开放的特点.解答方法具有一定的开放性，考查了学生的创新意识，为不同学生提供了展示才华的空间，激发学生的想象力，鼓励学生主动思考、发散思维.第（2）问题的证明，其思路可如图5，过点G作GH⊥CB于点H，通过证明△GHC≌△CBE，得CH=EB，从而证明CH=BH，结论获证.或思路如图6，过点G作GH⊥CB于H，连接DB，通过证明Rt△BCD≌Rt△CBE，得BD=CE，∠DBC=∠ECB，又∠ECB+∠GCH=90°，∠CGH+∠GCH=90°，故有∠ECB=∠CGH，∠DBC=∠CGH，Rt△GHC ≌ Rt△BCD，CD=CH，从而证明 CH=BH，结论获证.

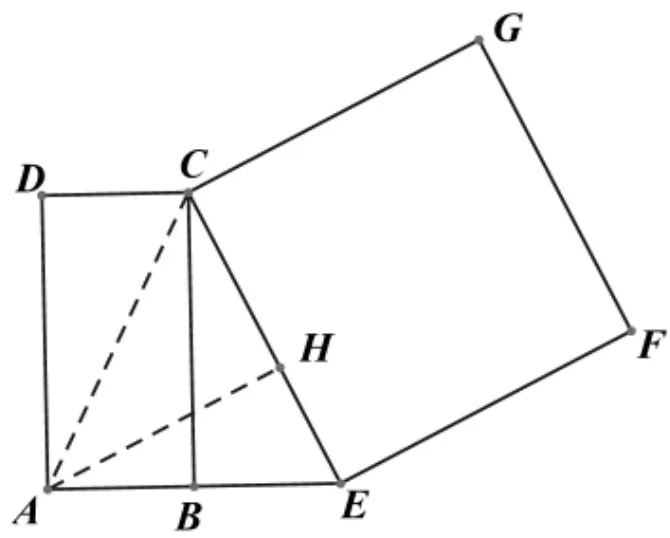
图4

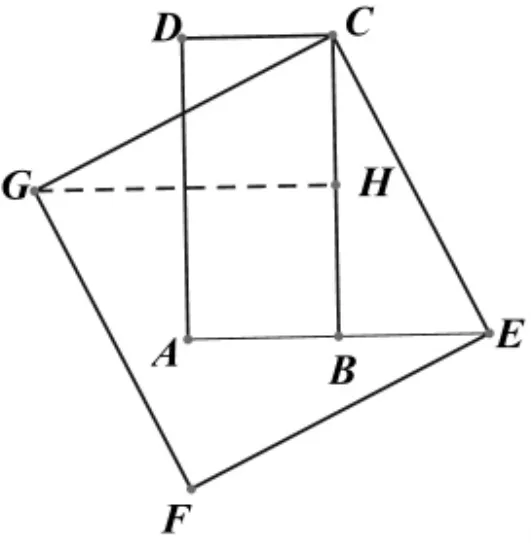
图5

图6

第（3）问题的证明，可采取几何法思路，如图7，过点F作FM⊥CB于点M，过点E作EN⊥MF于点N，通过证明Rt△FNE≌ Rt△CBE，得BE=NE，故BM=NE=BE，从而CM=BM，结论获证.也可采取几何思路，如图8，过点F作FM⊥CB于点M，过点F作FH⊥AE交AE的延长线于点H，得矩形BHFM，BM=FH，又可证Rt△FEH≌Rt△ECB，故有BE=FH=BM，从而CM=BM，结论获证.还可采取代数法思路，如图9，连接CF和BF，过点F作FN⊥AE交AE的延长线于点N，可证Rt△FEN≌Rt△ECB，FN=BE，EN=CB，若设BE=a，则对 Rt△CFG 和 Rt△BNF 可计算出 CG2=CE2=（2a）2+a2=5a2，CF2=5a2+5a2=10a2，BF2=（3a）2+a2=10a2，从而 CF=BF，F 在 BC 的垂直平分线上.

图7

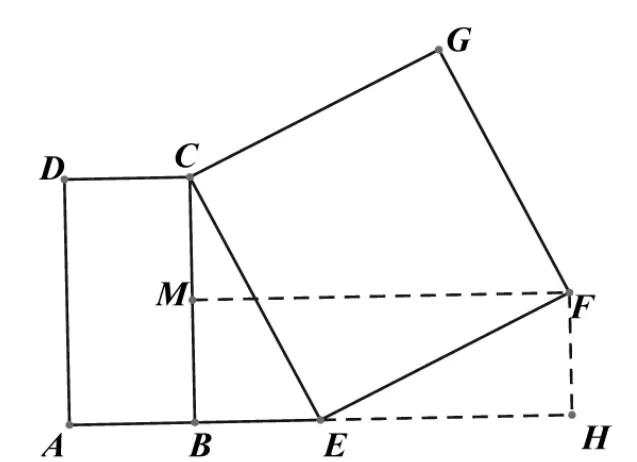
图8

图9

2.3 可拓思维的素材

对该试题探究还有可拓展的思维空间.若将试题作为教学活动继续探讨、研究的对象，沿着原试题情境中的方向往后思考的话，又会得到意想不到的结论.

对于“问题情境”环节的图1“以DE为一边在DE的左下方作正方形DEFG”对称变式为“以DE为一边和“在DE的右上方作正方形DEFG”（或再抽象为“以DE为一边作正方形DEFG”），结论是一样的.思考发现，实质上该问题只与“连接的DE，DE、BC的交点M”有关，而与是否构造正方形无关.设置构造正方形是为后继的问题提出做铺垫之用的.

若将图2、图3结合在一起思考，图2正方形沿直线CE翻折形成又一正方形.条件变成“以CE为一边作正方形，可有正方形CEFG、正方形CEF′G′”，得到如图10所示，连接GF′，则有GF′垂直平分边CB的特征.继续观察图10，去除多余的次要图形部分，抓住主干，可抽象成更为简单的图形图11.同时可对图11应有的类似结论进行归纳抽象，得“以某一线段为一边作两个不重叠的正方形，再以这一线段为直角三角形的斜边，构造一个两直角边边长是2倍关系的直角三角形，则由两个正方形构成的矩形存在一条对角线垂直平分直角三角形较长的直角边”.我们认为“数学抽象”虽是高中阶段的数学核心素养，让初中阶段学生进行这样的训练是很有必要的.

继续探究，以上在构造正方形时，都是连接最初图形中的点A、点B、点C、点D、点E中的某两点所成线段（非原图形的线段）作为正方形的一条边构造正方形去探索的.至此余下只有连接矩形对角线的情形了，那么连接矩形ABCD的任一条对角线，以此对角线为一边作正方形，结论又怎样？可以证明均有类似于上面的性质特征，即“存在正方形的某一顶点在矩形较长边的垂直平分线上”.事实上问题可转化为图11的情形，结论显然是成立的.

对于图10，可引导学生寻找、感悟图形之美，体会结论之美.图形中矩形的边长是2倍关系，直角三角形的直角边边长同样是2倍关系，得到的结论——出现有“线段垂直平分线”图形.

如上探究活动，程式具有一定的逻辑性，围绕同样的主线——点在线段的垂直平分线上，进行操作、观察、猜想、论证.得到的又有类似的结论——存在这样的点和线段，点在线段的垂直平分线上，体现出图形动态变化过程中的和谐美，体现出结论、规律的统一美，体现出事物间普遍联系的辩证唯物主义观点.

开拓思维空间，对原有22题的再探究，无论是在培养学生的探究思维能力，培养学生的创新精神方面，还是在引导学生揭示事物间的联系，发现结论、规律方面，无疑具有积极的促进作用.

图10

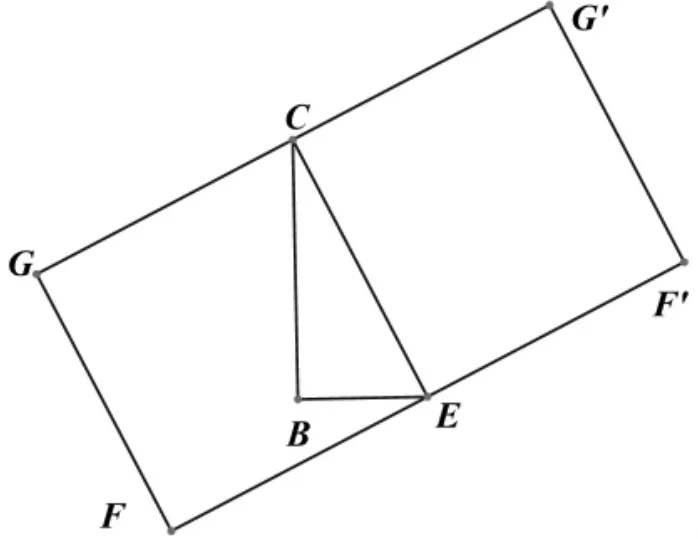
图11

3 小结

总之，数学教学不应满足于问题解答，而应善于挖掘发现问题、蕴含的教学资源，引导学生对问题进行深入的研究和探讨，培养学生勤于思考、勇于思考、善于思考的思维习惯，发展学生的数学思维能力和数学核心素养.