有限域Z2上线性方程组解的个数

闫慧凰，武惠俊

（长治学院数学系，山西长治046011）

1 有关符号说明和定义

Z2=｛｝表示模2的剩余类环，它是一个仅有两个元的有限域。为方便书写，文中分别用0，1表示，以后不专门说明.记对应方程组的解的个数为n.其余符号和术语与文献［1］［2］一致.

定义1 Z2上的线性方程组指形式为

的方程组，其中 x1，x2，…，xn代表 n 个未知量，s为方程的个数，并且 aij，bi∈Z2，（i=1，2，…，s，j=1，2，…，n）.

定义2（1）式中当bi=0（i=1，2，…，s）时的方程组称为 Z2上的齐次线性方程组.

2 Z2上的齐次线性方程组的解

定理1Z2上的n元单个线性方程的解的个数为个2n-1（n≥1）.

证明：（i）当n=1时，结论显然.

（ii）假设当n=k时，命题成立.即齐次线性方程组x1+x2+… +xk=0有2k-1个解（由于Z2中仅有0，1两个元素，由对称性则知方程组x1+x2+…+xk=1的解的个数也恰为2k-1个）.则当n=k+1时，齐次线性方程组x1+x2+…+xk+xk+1=0的解有且仅有以下两种情形：

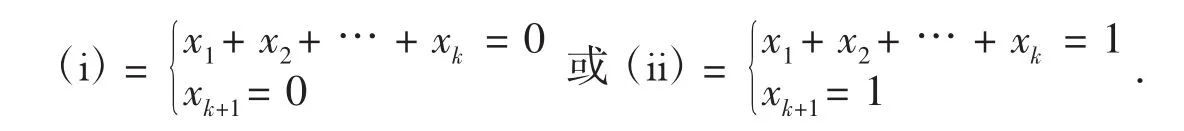
对于以上情形（i），解的个数显然为2k-1个；

对于以上情形（ii），解的个数显然也为2k-1个；则方程x1+x2+… +xk+xk+1=0的解的个数为：2k-1+2k-1=2·2k-1=2k=2（k+1）-1个.

故Z2上的n元单个线性方程的解的个数为2n-1个（n≥1）.

推论1对于Z2上的n元单个线性方程，若其中k个未知数的系数为1，其余n-k个未知数的系数为0，则方程的解的个数亦为2n-1个.

证明：对于系数均为1的k个未知数的方程，由定理1知，解的个数为2k-1个；对于系数为0的n-k个未知数，每个未知数的取值均有0，1两种可能，由乘法原理，则这n-k个未知数的总共取法为可得方程解的个数为2k-1·2n-k=2n-1，结论得证.

定理2Z2上的n元齐次线性方程组，若所含的方程个数为2个，则当r（A）=1时，解的个数为2n-1；当r（A）=2时，解的个数为2n-2.

证明：r（A）=1时，由定理1知，结论显然；

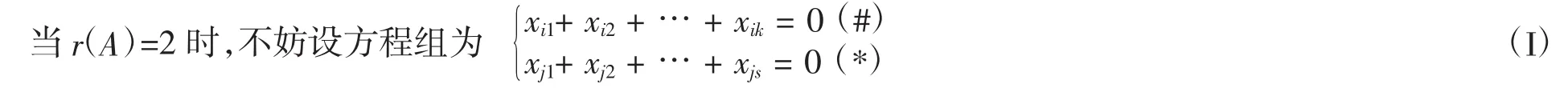
（其中 i1，i2，…ik及 j1，j2，…jk为 1，2，…，n 中的不同数码）.下面分三种情形分别予以证明：

（1）方程（#）中n个未知元全部出现，方程（*）中含方程（#）中的s个未知元（不妨设是前s个）.由定理2.1知，方程（*）的解的个数为 2s-1个，则

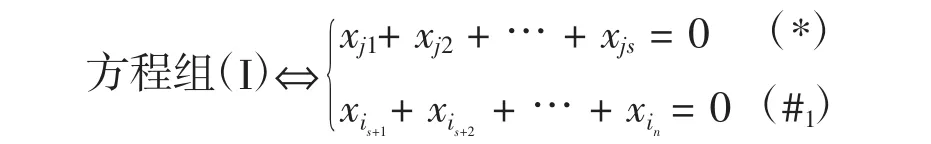
由于方程（#1）含有未知数的个数为 n-(s+1)+1 个，则方程（#1）的解的个数为 2［n-(s+1)+1］-1=2n-s-1个.由乘法原理，所以方程组（I）的解的个数为2s-1·2n-s-1=2n-2=2n-r（A）.

（2）方程（#）与（*）中n个未知元全部出现，有m个公共未知元，则方程（#）中除这m个公共元外还有k-m个元，方程（*）中除这m个公共元外还有s-m个元，即有k+s-m=n.这时，

其中，未知元 xi1，xi2，…，xim表示方程（#）与方程（*）的 m 个公共元；未知元 xim+1，xim+2，…，xik表示方程（#）中除去方程组（I）中的m个公共元外剩余的k-m个元；未知元表示方程（*）中除去方程组（I）中的m个公共元外剩余的 s-m 个元.结合定理 1，则方程组（I1）的解的个数为 2m-1·2［k-(m+1)+1］-1·2［s-(m+1)+1］-1=2k+s-m-3=2n-3.又由于Z2中仅有0和1两个元，有0和1的对称性，再由定理1，则方程组（I2）的解的个数也为2n-3个.所以，原方程组的解的个数为：2n-3+2n-3=2n-2=2n-r（A）.

（3）方程（#）与（*）无公共元，且设方程（#）中含有p个未知元，方程（*）中含有q个未知元.由定理1知，方程（#）的解的个数为2p-1，方程（*）的解的个数为2q-1，且方程组（I）中有n-p-q个自由未知量，每个量均有取0和1两种取法，共2n-p-q种取法.故有乘法原理，则方程组（I）的解的个数为2p-1·2q-1·2n-p-q=2n-2=2n-r（A）.

综上，对于Z2上的n元齐次线性方程组，若所含的方程个数为2个，则当r（A）=1时，解的个数为2n-1；当r（A）=2时，解的个数为2n-2.

定理3Z2上的n元齐次线性方程组，若其系数矩阵的秩为r（A），则方程组的解的个数n=2n-r（A）.

证明：设方程组为

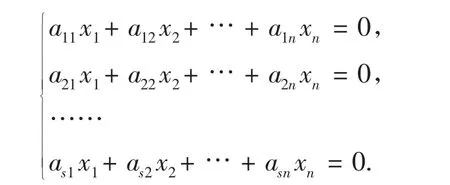
其中 aij∈Z2（i=1，2，…，s，j=1，2，…，n）.

对r（A）作数学归纳法.

当r（A）=1，r（A）=2时，由定理2结论成立.

假设系数矩阵的秩为r（A）-1时，结论成立.当系数矩阵的秩为r（A）时，对系数矩阵作初等行变换，得到最简阶梯形矩阵中有r（A）个非零行.记原方程组的解有n0个，注意到，第一行到第r（A）-1行组成的方程组与r（A）个非零行组成的方程组相比较，恰好多了一个自由未知量，而自由未知量有0，1两种取法.又由归纳假设得，第一行到第r（A）-1行对应的方程组有2n-r（A）+1个解，可以得到n0·2=2n-r（A）+1，故n0=2n-r（A），结论得证.