一类二阶离散左定Sturm-Liouville问题的谱

王雅丽， 高承华

(西北师范大学数学与统计学院, 兰州 730070)

1 引 言

近年来, 在许多物理问题中出现了边界条件依赖特征参数的S-L问题, 引起了诸多学者的广泛关注并获得了许多深刻结果[1-4]. 如文献[2]利用Prüfer变换研究了边界条件依赖特征参数的特征值问题的S-L理论, 得到了特征值的存在性, 交错性以及特征值对应特征函数的振荡性. 文献[4]得到了连续情形下问题的渐近公式及特征值的交错性, 对应特征函数的振荡性等性质.

对边界条件依赖于特征参数的离散右定S-L问题的谱的研究也已经取得了丰富的结果[5-9]. 如2016年, 文献[7]研究了如下边界条件依赖线性特征参数的离散右定S-L问题：

的谱， 其中m(t)>0,t∈[1,T]Z, 即m(t)在[1,T]Z上不变号.对于边界条件依赖特征参数的离散左定S-L问题的谱研究相对少见. 2017年, 文献[10]研究了边界条件依赖线性特征参数的离散左定S-L问题

的谱. 其中,r(t)在[1,T]Z上变号.受以上文献的启发, 本文研究如下二阶离散左定S-L问题

的谱, 这里Δ是前差分算子, 满足Δu(t)=u(t+1)-u(t),是后差分算子, 满足u(t)=u(t)-u(t-1),λ是谱参数,p:[0,T]Z→(0,+),q:[1,T]Z→(0,+),r(t)≠0且在[1,T]Z上变号. 进一步推广了文献[10]的结果.

2 预备知识

本文总假定:

(A1) 对所有的t∈[0,T]Z有p(t)>0, 对所有的t∈[1,T]Z有q(t)≥0;

(A2)r(t)在t∈[1,T]Z上变号, 即在[1,T]Z上有m个点使得r(t)>0, 另外T-m个点使得r(t)<0；

(A3)δM正定， 其中δ=ad-bc,

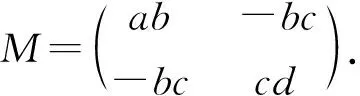
由(A3)可知,δab>0,δcd>0且detM=δbc>0, 于是ac>0,bd>0.

设y(t,λ)是方程(1)满足初始条件

y(0,λ)=p(0)(cλ+d),Δy(0,λ)=aλ+b

(3)

的解, 则y(t,λ)为如下广义Sturm序列:

y(0,λ)=p(0)(cλ+d);

y(1,λ)=(a+p(0)c)λ+(b+p(0)d);

(a+p(0)c)λi+Pi-1(λ),i=2,…,T

(4)

这里Pi-1(λ)是关于λ的i-1次多项式. 特别地,

(a+p(0)c)λT+1+PT(λ).

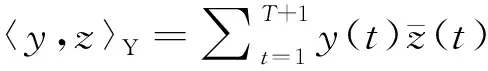
定义H:=Y⊕C. 则H在内积

之下构成Hilbert空间.

定义A:D(A)→H，

A(y,α)=(-(p(t)Δy(t))+q(t)y(t),

-ε(by(0)-dp(0)Δy(0))),

其中D(A)={(y,α)y∈Y, -ay(0)+cp(0)Δy(0)=α},ε=sgnδ. 于是问题(1)-(2)等价于AY=λSY， 这里S=(y,α)=(ry,α).

引理2.1算子A在D(A)上是正定的.

证明 由Hilbert空间中内积的定义可得

这里f=(y(0),p(0)Δy(0))T, 于是由(A1)及(A3)可知算子A正定.

3 主要结果

引理3.1多项式y(t-1,λ)与y(t,λ),t=1,…,T+1无相同零点.

证明 反设λ=λ0是y(t-1,λ)与y(t,λ)的零点. 则由(4)式可得y(t-2,λ0)=0. 进一步可得y(t-3,λ0)=…=y(1,λ0)=y(0,λ0)=0. 这与y(1,λ0)≠y(0,λ0)=0矛盾.

引理3.2设λ=λ0是y(t,λ)=0的零点, 则y(t-1,λ0)y(t+1,λ0)<0.

证明 由于y(t,λ0)=0, 由引理3.1可知y(t-1,λ0)≠0. 于是由(4)式可知

因此

y(t-1,λ0)y(t+1,λ0)=

由(7)式可知,y(T+1,λ)的最高次项为

(a+p(0)c)λT+1.

因此当λ足够大时,y(t,λ)的符号取决于a+p(0)c的符号. 若a+p(0)c>0, 则

sgny(T+1,λ)=(-1)T-m+1,λ→-;

若a+p(0)c<0, 则

sgny(T+1,λ)=(-1)T-m,λ→-.

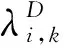
t∈[1,i-1]Z

和方程(1)以及y(i)=0组成问题的特征值. 特别地

则

所以不失一般性接下来我们总假定

(A4)δ<0,c<0.

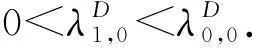
引理3.3多项式y(i,λ)=0与y(i+1,λ)=0,i=1,…,T的根满足如下交错性质：

(ii)y(i,λ)=0与y(i+1,λ)=0,i=1,…,T的正(负)根互相分离.

所以当r(1)>0时, 若λ→-则y(2,λ)→+; 若λ→+则y(2,λ)→+.于是y(2,λ)=0有两个正根且满足当r(1)<0时, 若λ→-则y(2,λ)→-; 若λ→+则y(2,λ)→-. 于是y(2,λ)=0有一个负根一个正根且满足因此,y(1,λ)=0与y(2,λ)=0分别有1个, 2个单根且正(负)根互相分离.

不妨假设i=k-1时结论成立, 即y(k-1,λ)=0与y(k,λ)=0分别有k-1个、k个单根且正(负)根也有交错性. 为简单起见令

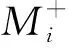
接下来考虑y(k,λ)=0与y(k+1,λ)=0的根的交错性. 不妨设r(k)>0, 则r(t)在[1,k]Z上有mk-2+2个为正以及k-2-mk-2个为负. 由(4)式可知sgny(k+1,-)=-sgny(k,-),sgny(k+1,+)=-sgny(k,+),以及y(k+1,0)>y(k,0)>0, 且由引理3.2可知

u=1,2,…,mk-2+2,

v=1,2,…,k-2-mk-2.

内各有y(k+1,λ)=0的一个根. 另一方面,y(k+1,λ)=0至多有k+1个根. 于是在这k+1个区间内y(k+1,λ)=0只有一个根. 因此y(k,λ)=0与y(k+1,λ)=0的正(负)根互相分离.综上可知,y(i,λ)=0与y(i+1,λ)=0,i=1,…,T的正(负)根互相分离.证毕.

推论3.4由引理3.3可知, 问题(1),(3)恰有T+1个特征值且满足

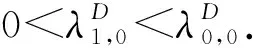
引理3.5假设(A1)～(A4)成立, 则

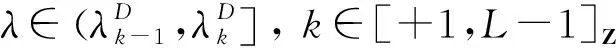
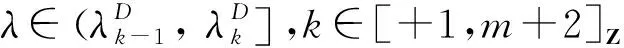
{y(1,λ), …,y(T,λ),y(T+1,λ)}

(5)

变号k-1次. 接下来讨论如下序列的变号次数

{y(0,λ),y(1,λ),…,y(T,λ),y(T+1,λ)}

(6)

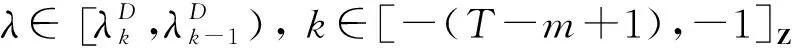
定理3.6假设(A1)～(A4)成立, 则

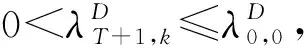
例3.7考虑如下离散左定S-L问题:

其中, |r(t)=16|,r(1)>0,r(2)>0,r(3)<0.则

y(0,λ)=-λ+1,

y(1,λ)=-4λ+3,

y(2,λ)=(2-r(1)λ)y(1,λ)-y(0,λ),

y(3,λ)=(2-r(2)λ)y(2,λ)-y(1,λ),

y(4,λ)=(2-r(3)λ)y(3,λ)-y(2,λ),

由Matlab 7.0软件计算可得,

即

这与引理3.3的结论一致且问题共有4个特征值, 其中有1个负特征值, 3个正特征值. 接下来我们来验证振荡性.

{0.1067, 3.4267, 11.5957, 39.5568, 0},

{0.9599, 2.8396, 2.8978, 1.0970, 0},

{0.8301, 2.3205, -2.4958, -0.5290, 0},

{0.2439, -0.02439, 0.002399, 0.0001702, 0}.

从而可知问题的解y(t,λ),t=0, 1, 2,3,4变号k-1次.这与定理3.6的结论一致.