一维非稳态半导体漂移扩散模型的弱Galerkin有限元法
朱紫陌, 李鸿亮, 张世全
(1. 四川大学数学学院, 成都 610064; 2. 中国工程物理研究院电子工程研究所, 绵阳 621900)
1 引 言
设I=(0,1),J=(0,T],T<.考虑下述非稳态漂移扩散模型:求静电势Ψ(x,t)和电子浓度n(x,t)满足
nt-Dnnxx+μn(nΨx)x=0, (x,t)∈I×J
(1)
对应的边值条件和初值条件为
Ψ(0,t)=gΨ0(t),Ψ(1,t)=gΨ1(t),n(0,t)
=gn0(t),n(1,t)=gn1(t),∀t∈J
(2)
n(x,0)=n0(x),∀x∈I
(3)
其中ε>0是半导体的介电常数,q是电子电荷量,f(x,t)是掺杂浓度函数,Dn代表电子的扩散系数,μn代表电子迁移率.更一般的漂移扩散模型还会考虑空穴电流连续性方程和复合率项,但本文仅考虑简化后的单粒子模型.
针对这类偏微分方程,理论和数值研究已有很长的历史.对于漂移扩散模型的稳态及非稳态解在一些特定条件下的存在唯一性证明,可以参考文献[1-6]及其引用文献.另一方面,数值研究开始于二十世纪六十年代.文献[7]给出了求解一维稳态模型的自洽迭代格式.在接下来几十年,也有许多离散方法用于求解漂移扩散模型,例如有限差分法[8-11],有限体积法[12-16],标准的有限元法[17-19],以及混合有限元法[20-22].
对于漂移扩散模型,由于半导体器件损伤通常会产生漂移和扩散系数间断现象,因此间断有限元法常被用来离散问题(1)~(3).在文献[23]中,一种局部间断有限元方法被用来求解一维漂移扩散方程,并得到了半离散和全离散格式的最优误差估计.在文献[24-25]中, Wang和Ye最早提出用于求解二阶椭圆问题的弱Galerkin有限元法.其主要思想是在广义函数空间上引入一种弱梯度算子,利用弱梯度算子来离散变分问题.这种方法能够保持局部消除的性质.此外,弱Galerkin有限元法还被广泛应用于求解各种偏微分方程[26-34].
本文考虑用一种弱Galerkin有限元法来离散问题(1)~(3),引入弱函数v={v0,va,vb},采用分片k次多项式来逼近弱函数的内部v0.
本文结构如下:第二节给出基本记号、弱问题以及离散弱导数的定义;第三节引入半离散弱Galerkin有限元格式;第四节给出半离散格式的误差估计;第五节给出数值实验结果.
2 预备知识
2.1 基本记号

空间Hl(0,T;Hs(I))定义为
Hl(0,T;Hs(I))=
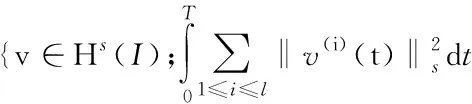
其中v(i)(t)是v关于t的i阶导数.相应的范数定义为
引理2.1(Gronwall不等式[35]) 令u(t),α(t),β(t)是定义在[a,b]上的实连续函数,且对任意的t∈[a,b]有β(t)≥0.假设
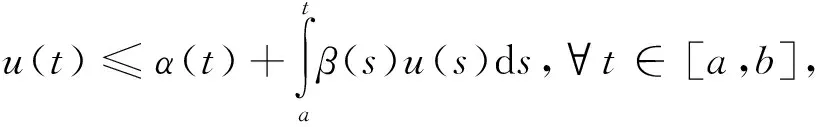
则有
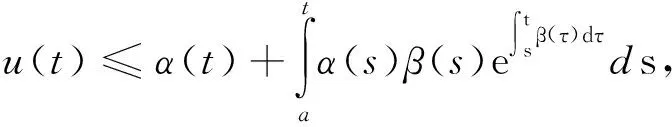
∀t∈[a,b].
2.2 弱问题
首先,我们引入函数集合



及下列双线性和三线性形式:对任意的Ψ∈V1,n∈V2和v,w∈V,


-μn(nΨx,wx).
于是,问题(1)~(3)的变分问题为:求 (Ψ,n)∈V1×V2满足
A(Ψ,n;v)=(f,v),∀v∈V,
(4)
其中

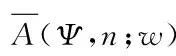
引理2.2[34]∀t∈J,f(x,t)∈L(I),初值n0(x)∈L(I)且在I上几乎处处大于0,边值gn0(t),gn1(t)>0,迁移率μn是正常数时,弱问题(4) 存在唯一解.
2.3 离散弱导数
W(Ia)={v={v0,va,vb}:v0∈L2(Ia),
|va|+|vb|<}.
对任意非负整数r,定义Pr(Ia)为单元Ia上次数不超过r的所有多项式的集合.为了构造问题(1)~(3)的弱Galerkin有限元格式,我们引入离散弱导数算子dw,r如下.
定义2.3对v∈W(Ia),其离散弱导数dw,rv∈Pr(Ia)的定义由以下方程给出
∀q∈Pr(Ia)
(5)
其中qa=q(xa),qb=q(xb).
3 半离散弱Galerkin有限元格式
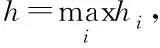
Sh={v={v0,vL,vR}:v0|Ii∈Pk(Ii),vL|Ii
=vi,vR|Ii=vi+1,|vi|+|vi+1|<,
i=1,2,…,N-1},
(6)
(7)
定义离散的L2内积和范数为
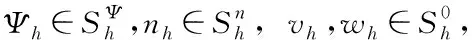




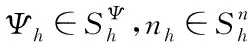
(8)
其中

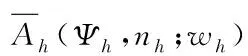
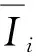
证明 首先,令v0=vi=vi+1.由(5)式可得
∀q∈Pr(Ii).
这表明dw,rv=0.接下来令dw,rv=0.由(5)式可得
∀q∈Pr(Ii)
(9)
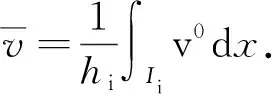
(10)
显然,问题(10)存在唯一解q1∈Pr(Ii).对(10)式积分得到
q1,i=vi+1-vi.
因此,在(9)中取q=q1可得

因此v0=vi=vi+1.证毕.
引理3.1表明离散弱导数dw,rv保持了经典导数v′的重要特征.
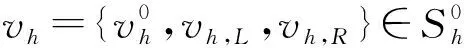
(11)
证明 由dw,rvh的定义,在(5)式中取q=1得到
(12)
在各单元上求和并利用vh,1=0可得
(13)
令q1∈Pr(Ii)满足以下初值问题
(14)
在(5)式中取q=q1可得
vh,iq1,i-vh,i+1q1,i+1
(15)
对(14)式积分得到
(16)
将(16)式代入(15)式并利用(12)式,得
因此由Cauchy-Schwarz不等式和估计式(13)可以得到
证毕.
4 误差估计
本节将给出半离散弱Galerkin有限元格式(8)的误差估计.
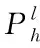
i=1,2,…,N-1.
由Bramble-Hilbert引理,易知
(17)
定义投影算子Qh:u∈H1(I)→Qhu∈Sh如下:
i=1,2,…,N-1.
由(17)式可知
(18)
进一步,利用投影算子Qh和离散弱导数dw,r的定义,有如下交换性质:

0≤s≤k+1
(19)
为了得到误差估计,我们还需要引入下述投影函数.
定理4.1对任意的u∈H1(I),存在πhu∈H1(I), 使得πhu|Ii∈Pk+1(Ii)并且满足
((πhu)′,q)Ii=(u′,q)Ii,∀q∈Pk(Ii),
i=1,…,N-1
(20)
πhu(xi)=u(xi),i=1,…,N
(21)
进一步,对0≤s≤k+1,有
‖u-πhu‖Ii+hi‖u-πhu‖1,Ii≤
(22)
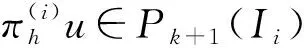
(23)
(24)
0≤s≤k+1
(25)
因为
所以由(24)式以及Cauchy-Schwarz不等式可以得到
(26)
(27)
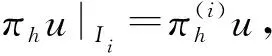
引理4.2若Ψ,n∈H1(0,T;H2(I))是问题(1)~(3)的解,则
dw,rwh)h-μn(πh(nΨx),dw,rwh)h=0,
(28)
(29)
由(20)式可知
(30)
由离散弱导数算子dw,r的定义,有
dw,rwh)Ii+μn(πh(nΨx))i+1wh,i+1-
在各单元上求和并且注意到wh,1=0和wh,N=0,有
(31)
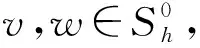
(32)
Dn(πhnx,dw,rwh)h
(33)
将(31)~(33)式代入(29)式即得(28)式.证毕.
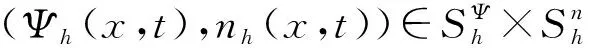
(34)
(35)
其中正常数C与Ψ和n在每个时刻的H2范数和Hk+2范数有关.
(36)
和
Dn(dw,r(Qhn-nh),dw,rwh)h=
Dn(dw,rQhn,dw,rwh)h-Dn(πhnx,dw,rwh)h+
μn(πh(nΨx),dw,rwh)h-
(37)
在(36)式中令vh=QhΨ-Ψh并利用Cauchy-Schwarz不等式, 引理 4.1和引理 3.2,可以得到
Chk+1‖Ψ‖k+2‖dw,r(QhΨ-Ψh)‖h+
(38)
于是
‖dw,r(QhΨ-Ψh)‖h≤Chk+1‖Ψ‖k+2+
(39)
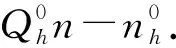
(Dn(dw,rQhn-nx,dw,r(Qhn-nh))h-
Dn(πhnx-nx,dw,r(Qhn-nh))h)+
(μn(πh(nΨx)-nΨx,dw,r(Qhn-nh))h+
μn(n(Ψx-dw,rQhΨ),dw,r(Qhn-nh))h)+
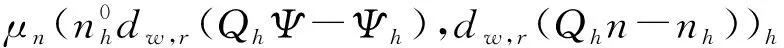
R1+R2+R3+R4+R5
(40)
由Cauchy-Schwarz不等式,投影性质,引理 4.1和Young不等式,可得
R1≤Chk+1‖n‖k+2‖dw,r(Qhn-nh)‖h≤
(41)
R2≤Chk+1‖n‖2‖Ψ‖k+2‖dw,r(Qhn-
(42)
R3≤Chk+1‖Ψ‖2‖n‖k+2‖dw,r(Qhn-
(43)
(44)
为了估计R5,我们先假设
(45)
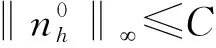
R5≤Cμn‖dw,r(QhΨ-Ψh)‖h‖dw,r(Qhn-
nh)‖h.
由(39)式和Young不等式可得
(46)
将(41)~(44)式,(46)式代入(40)式,得到
(47)
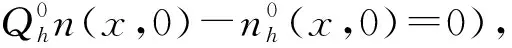
Ch2k+2
(48)
于是我们由(39)式,引理 3.2,三角不等式和投影性质得到误差估计(34)式和(35)式.
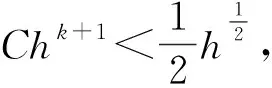

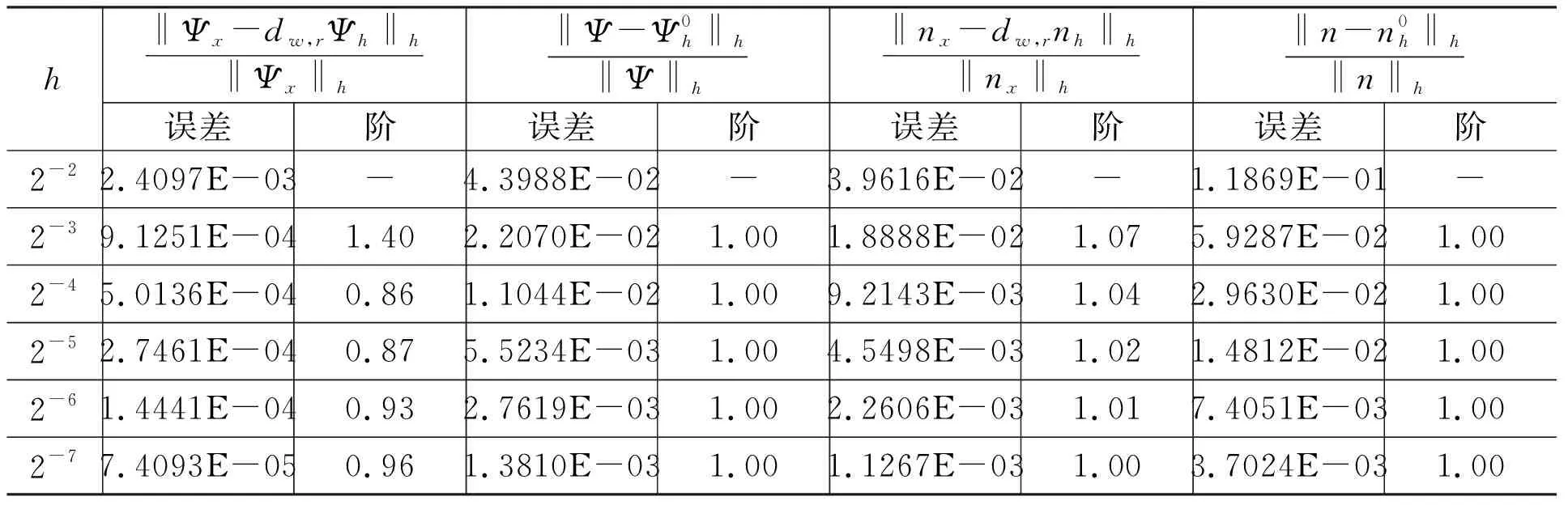
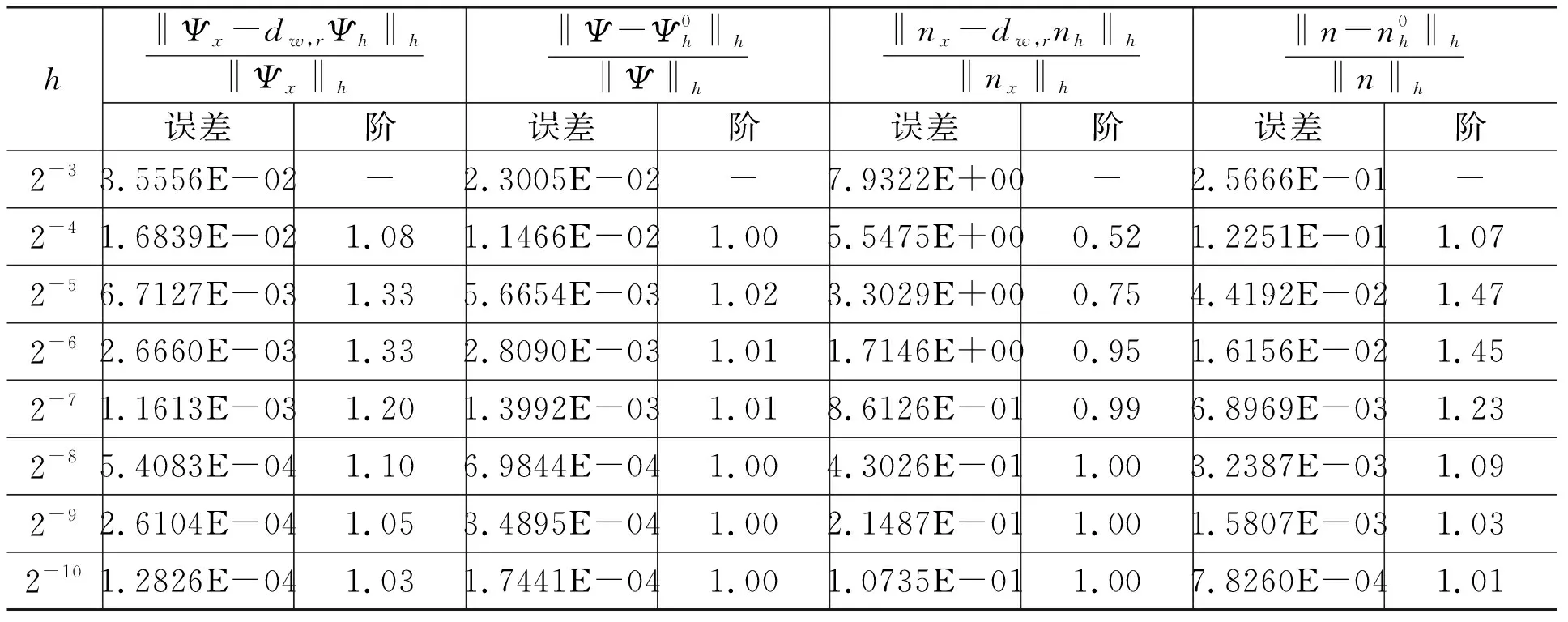
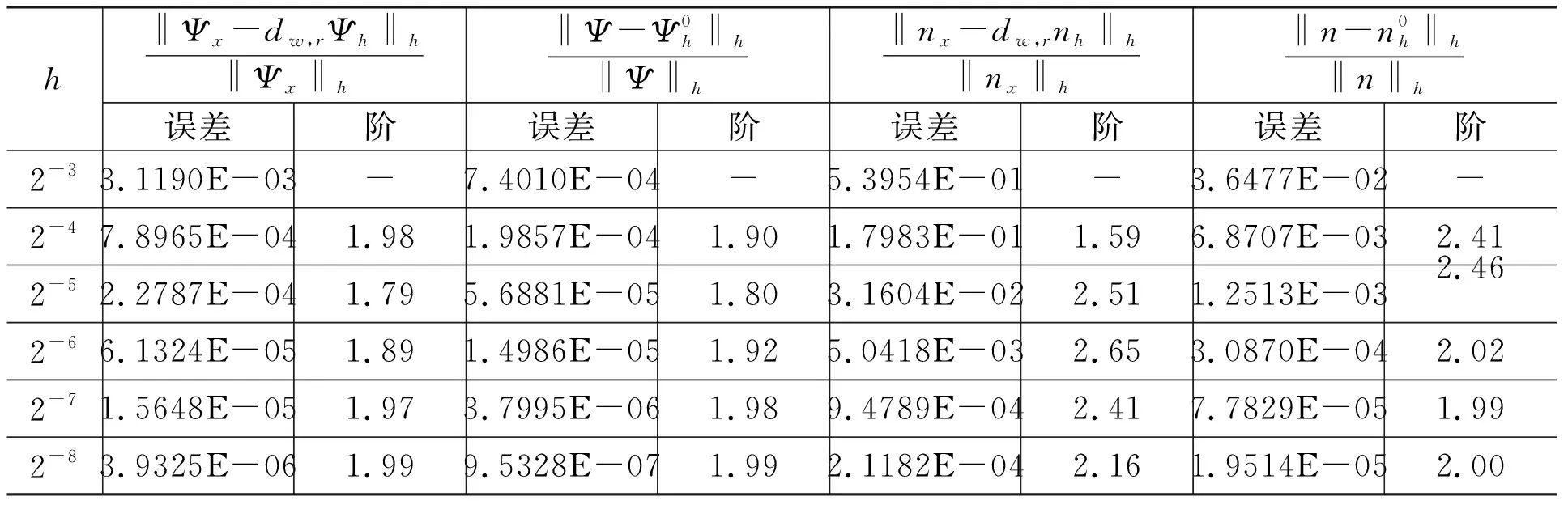
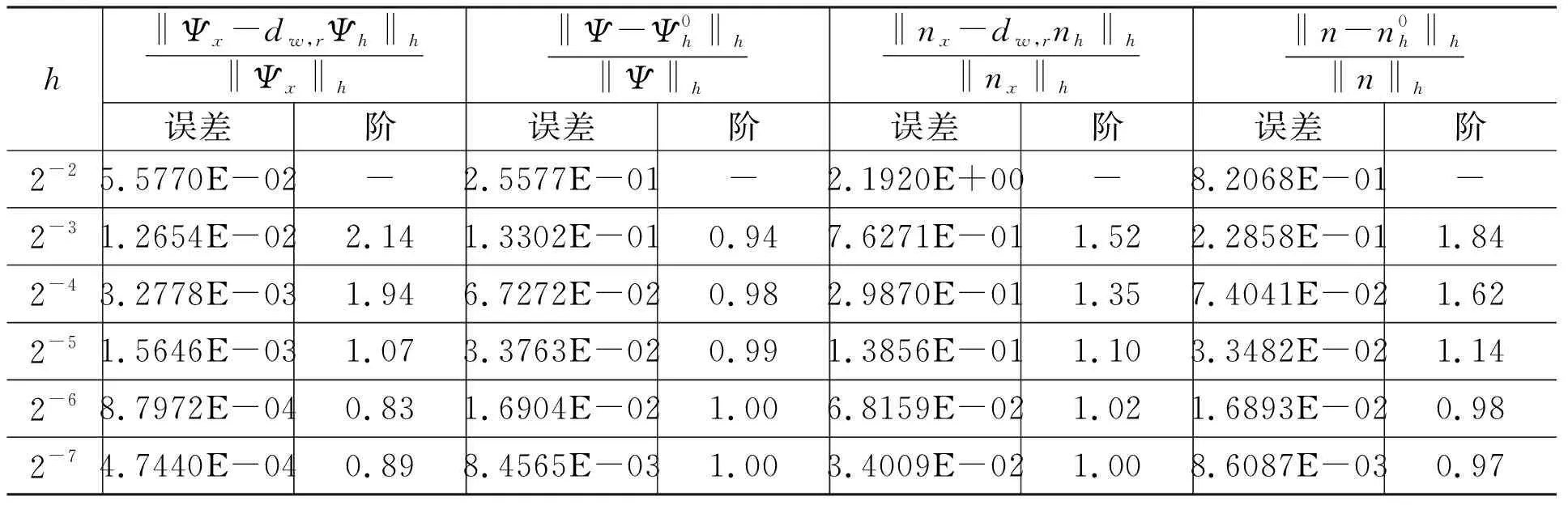
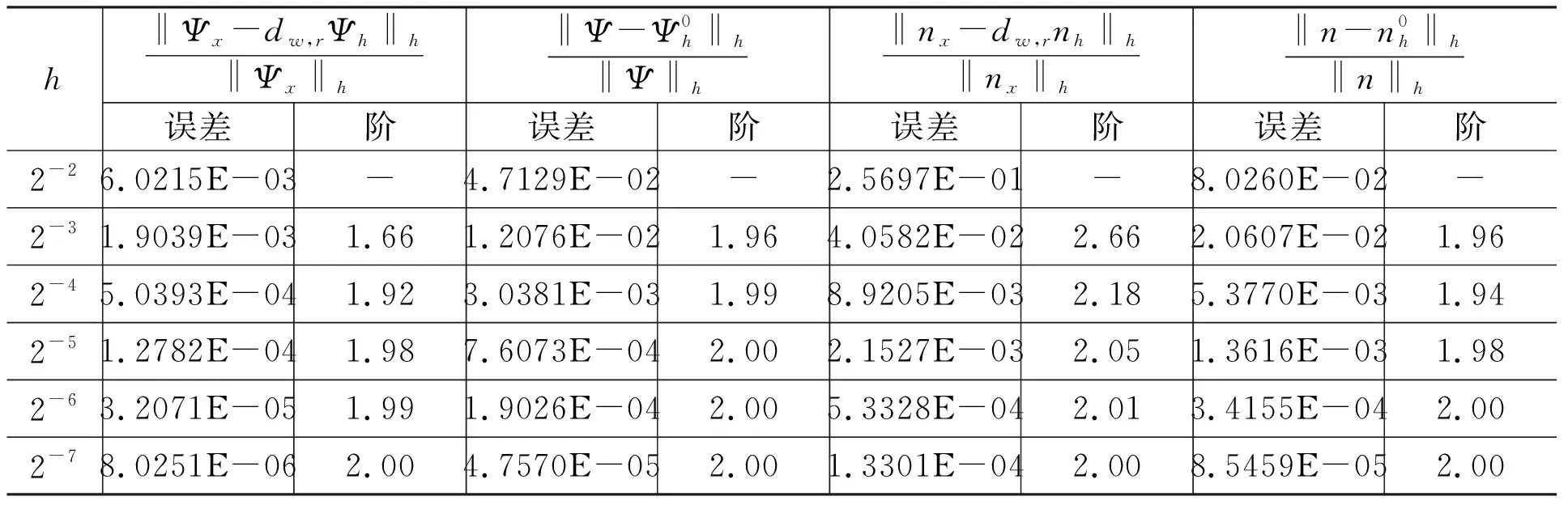
且t* 我们由连续性应得到 另一方面,我们的证明表明(34)式和(35)式对任意的t≤t*成立.特别地 这与t* 本节将给出两个数值算例.时间离散我们都采用向后欧拉差分格式: (49) 其中指标(m,r)分别代表时间迭代和非线性迭代的步数. 空间离散我们选择多项式次数为k=0或k=1.当k=0时,时间步长选择为Δt=h;当k=1时,时间步长选择为Δt=h2.计算时我们采用均匀加密的网格,我们将给出在最终时刻T=1时的误差. 例5.1令I=[0,1],J=[0,1],问题(1)~(3)的真解为 Ψ=sin(t)cos(x), (x,t)∈I×J, n=cos(t)sin(x), (x,t)∈I×J. 表1 Dn=1,k=0时例5.1的数值结果 表2 Dn=1,k=1时例5.1的数值结果 表1和表2分别给出了Dn=1时用分段常数和间断分段线性多项式求解算例5.1的数值结果,得到的误差收敛阶与理论一致. 表3 Dn=10-3,k=0时例5.1的数值结果 表4 Dn=10-3,k=1时例5.1的数值结果 表3和表4分别给出了Dn=10-3时用分段常数和间断分段线性多项式求解算例5.1的数值结果.可以看到,在用低次元求解小参数问题时,在粗网格下‖nx-dw,rnh‖h的相对误差较大,但随着网格的加密,得到的误差收敛阶与理论一致. 例5.2考虑带间断系数的算例.令I=[0,1],J=[0,1].问题(1)~(3)的真解为 Ψ=sin(t)x(x-1)2,x∈I, n=cos(t)x(1-x),x∈I. 表5 k=0时例5.2的数值结果 表6 k=1时例5.2的数值结果 表5和表6分别给出了用分段常数和间断分段线性多项式求解算例5.2的数值结果,得到的误差收敛阶与理论一致. 本文研究了一维非稳态半导体漂移扩散模型的弱Galerkin有限元法,通过恰当的空间匹配,我们得到了关于静电势Ψ和电子浓度n的最优误差估计,同时该方法还能处理间断系数问题.5 数值算例
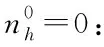
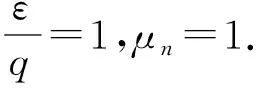

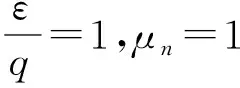
6 结 论

