关于Bergman 空间上复合算子的复对称性

宏俊颖， 韩学红

(天津大学数学学院， 天津 300354)

1 引 言

设L(H)为可分的复Hilbert空间H上所有有界线性算子组成的代数.对任意的x,y∈H，任意复数集C中的元素α，β，若算子C:H→H满足：

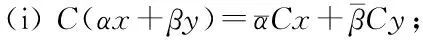
(ii) 〈Cx,Cy〉=〈y,x〉；

(iii)C为对合算子，即C2=I，这里I为恒等算子；

则称算子C是H上的共轭. 算子T∈L(H)称为复对称的是指存在H上的共轭C使得T=CT*C成立. 此时，称T关于共轭C是复对称的.

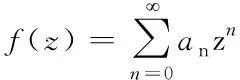
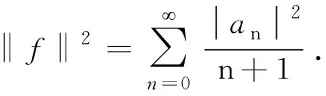
设D为复平面C上的单位圆盘，H(D)和S(D)分别表示单位圆盘上的所有解析函数和所有全纯自映射的集合. 由φ∈S(D)所诱导的复合算子Cφ定义为

Cφf(z)=f∘φ(z)，f∈H(D)，z∈D.

给定ψ∈H(D)，乘积算子Tψ定义为Tψ(f)(z)=ψ(z)·f(z)，f∈H(D).

2006年，Garcia和Putinar[1]将复对称矩阵的概念推广到Hilbert 空间，引入了复对称算子的概念.此后算子的复对称性被广泛研究. 首先是Garcia[2]指出了所有正规算子都是复对称的.紧接着，Garcia 和Hammond[3]研究了加权Hardy空间上(加权)复合算子的复对称性.其后，Jung等人[4]在文献[3]的基础上进一步研究了加权Hardy空间上(加权)复合算子的复对称性.其中，作者给出了一些非正规的复对称算子的例子.Bourdon和Noor[5]指出Hardy空间上复合算子Cφ是复对称算子的必要条件是φ在D内有Denjoy-Wolff点或φ是椭圆自同构，同时指出阶数大于3的椭圆自同构诱导的复合算子不是复对称的.最近，Gao和Zhou[6]指出Hardy空间上阶数等于3的椭圆自同构诱导的复合算子也不是复对称的，并且他们也完整地刻画了由分式线性变换诱导的复合算子的复对称性.此外，Narayan等人在文献[7]中还给出了Hardy空间上由非自同构的线性分式映射所诱导的复合算子是复对称而非正规算子的例子.

相比Hardy空间，Bergman空间上复合算子的复对称的研究结果较少.除了在文献[3]中有所涉及(因为加权Hardy空间包含Bergman空间的情形)外，只有Eklund等人[8]最近将文献[5]中的结果推广到Bergman空间得到类似的结果：Bergman空间上的复合算子Cφ是复对称算子的必要条件是φ在D内有Denjoy-Wolff点或φ是椭圆自同构，且阶数大于5的椭圆自同构诱导的复合算子不是复对称的.

本文在文献[8]的基础上将文献[7]的结果部分推广到Bergman空间上，给出了Bergman空间上由非自同构的线性分式映射所诱导的复合算子是复对称而非正规的例子. 由于 Hardy空间与Bergman空间核函数的不同导致Cowen 自伴公式(本文的引理2.1)也有所差异， 本文的证明思路与文献[7]基本一致，但是在Bergman空间上对函数ζ,ψ的选取和一些细节的计算却与Hardy空间不同. 本文主要结论如下:

定理1.1设σ(z)=az+c∈S(D)且非恒等映射，则Cσ在A2(D)上是复对称的当且仅当σ在D内有Denjoy-Wolff点并且无边界不动点.

注由文献[9]中定理8.2知，Cφ是A2(D)上的正规算子当且仅当φ(z)=az且|a|≤1，故由定理1.1知，当c≠0且σ(z)满足定理1.1的条件时，Cσ是复对称算子，但不是正规算子.

2 预备知识

线性分式映射

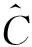
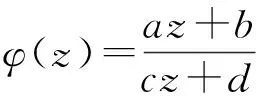
定理中的ω称为φ的Denjoy-Wolff点. 值得一提的是，Cφ的性质与Denjoy-Wolff点密切相关.

3 复对称复合算子的例子

本节我们将给出定理1.1的证明. 首先，我们给出共轭算子的一些基本性质.

引理3.1(文献[7]，命题2.1) 设J1和J2是可交换的等距算子且均为对合，且其中之一为线性而另一个为共轭线性，则J1J2是一个共轭.

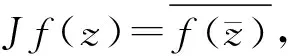
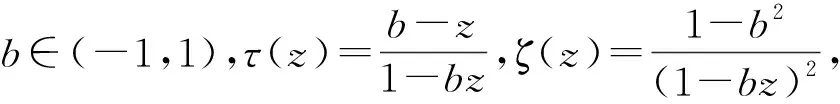
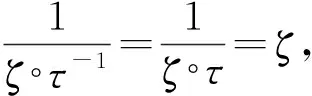
(1)

h(z)=(1-bz)2.

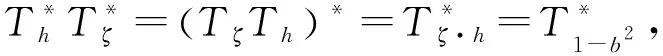
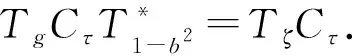
这表明TζCτ是自伴的.再由(1)式，TζCτ是酉算子.由b∈R，易知J和TζCτ是可交换的. 因此，由引理3.1，JTζCτ是一个共轭. 证毕.

下面的引理容易由引理2.1直接得到，我们略去证明.

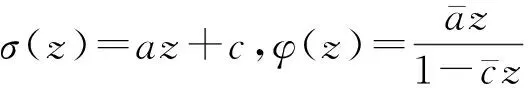
接下来，我们讨论当σ(z)=az+c时Cσ的形式.

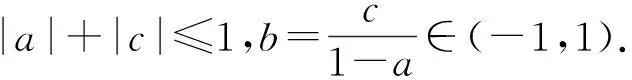
证明 这一结论可通过简单的计算得到，本文只给出大概过程.

首先，对任意的f∈A2(D)有

JTζCτTψCφJTζCτf(z)=JTζCτTψCφJTζf(τ(z))=

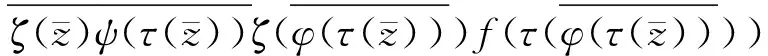
(2)

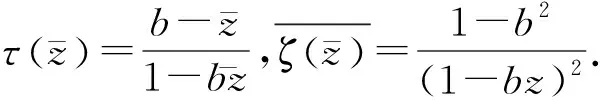
(3)

az+b(1-a)=σ(z)

(4)

(5)

(6)

结合(2)～(6)式有

f(σ(z))=f(σ(z))=Cσf(z).

因而Cσf(z)=JTζCτTψCφJTζCτf(z)对任意的f∈A2(D)均成立. 证毕.

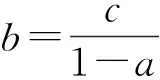
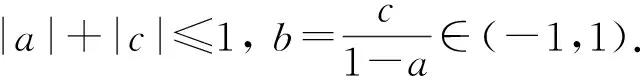
由引理3.2知这里的JTζCτ是一个共轭，故Cσ关于共轭JTζCτ是复对称的. 证毕.

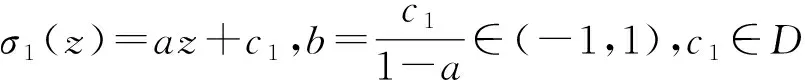
U-θCσ1Uθf(z)=U-θCσ1f(eiθz)=

U-θf(eiθσ1(z))=f(eiθσ1(e-iθz))=

f(σ(z))=Cσf(z)，

这里σ(z)=az+c，c=c1eiθ.这表明Cσ1和Cσ是酉等价的. 因此，由θ∈R的任意性知，对所有满足条件的σ，Cσ也是复对称的. 证毕.

定理 1.1的证明 若c=0，且σ不是恒等映射，则σ有唯一不动点为原点且没有边界不动点. 另外，根据文献[9]的定理 8.2得Cσ是A2(D)上的正规算子，Cσ一定是复对称的. 定理显然成立.