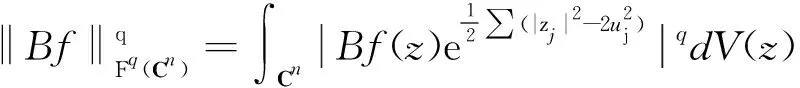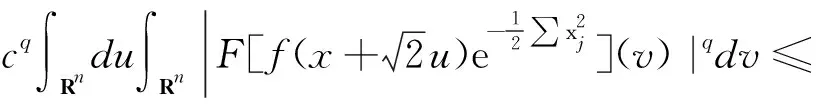高维空间中的Bargmann变换的有界性
郑佳鸿
(华南农业大学数学与信息学院, 广州 510640)
1 引 言
Bargmann 变换在数学物理和分析学中起着重要作用,更是连接实函数空间与复函数空间之间的桥梁,深受人们的重视[1-15].
关于Bargmann变换的研究已有五十多年的历史. 上世纪六十年代初,Bargmann[1]首次介绍了该积分变换. Bargmann找到了一个积分核, 把实空间中平方可积函数的希尔伯特空间与Fock空间中的算子关联起来. 在文献[2]中, Bargmann将该方法应用于tempered distribution的理论, 研究了Fock空间中的调和多项式和及其相应的分解. 之后, 人们对其展开了更深入的研究. 首先是将其应用于量子力学和热方程中[12], 后来也将其用于光学和信号处理[8,11].关于Bargmann变换的研究也可参见文献[14, 3, 5, 9]. 其中, Dong 等[5]研究了Bargmann变换对几个经典积分算子的作用, 包括分数阶傅里叶变换、分数阶希尔伯特变换和小波变换. 但这些研究仅限于一维情况下的 Bargmann变换等. 在n维空间上, Toft[7]研究了Bargmann变换下的函数图像和分布空间. Yoshino[13]推导出具有Bargmann-Fock空间中的多径向符号的Toeplitz算子特征值的公式, 并阐明了Bargmann-Fock 空间中的Toeplitz 算子与L2(Rn)中的Daubechies算子之间的关系. 但他们所研究的结果仅限于在L2(Rn)上的Bargmann变换, 即p=2的情形.
高维与一维情况下的解析函数空间及算子结构有着本质不同. 我们以Hartogs现象为例[10]. 设D是n>1维复空间Cn中的域,K为域D中的紧子集, 且DK为连通子集, 即D的子域. 若DK上的函数f全纯, 则f可解析开拓到域D上. 这在一维情况下则完全不同. 本文引理2.1当n=1与n>1的证法也不同.
本文研究n≥2维情况下的Bargmann变换, 主要针对p≠2的情形进行讨论.
2 预备知识
设Rn为n维实欧氏空间,Cn为n维复欧氏空间,d(x1,…,xn)和dV分别代表Rn和Cn上的勒贝格测度, 简记d(x1,…,xn)为dx. 若z=(z1,…,zn)=u+iv,w=(w1,…,wn)为Cn上两点, 记
对于0 f∈Fp(Cn). 对p=,f∈F(Cn), 记 f∈F(Cn). 显然, Fock空间Fp(Cn)在上述范数下为Banach空间, 其中1≤p≤. 特别地,F2(Cn)是Hilbert空间 更多关于Fock空间的研究结果可参见文献[14]. 定义2.1对任意f∈Lp(Rn), 定义 命题 2.2对任意f∈Lp(Rn), 1≤p≤, Bargmann变换是良定义的. 证明 令z=u+iv,z∈Cn.则有 (1) 且 (2) 若f∈L1(Rn), 则 (3) 若f∈L(Rn), 则 |Bf(z)|≤c‖f‖ (4) 若f∈Lp(Rn), 1 (5) 可见,对任意f∈Lp(Rn), Bargmann变换Bf是良定义的. 引理 2.3[1]Bargmann 变换是从L2(Rn)到F2(Cn)的酉算子. 证明 事实上, 记F为Fourier变换. 对z∈Cn,zj=uj+ivj, 易得 (6) 引理3.1对任意0 ‖Bf‖Fp(Cn)≤C‖f‖Lp(Rn), f∈Lp(Rn)∩L1(Rn) (7) 证明 反证法.若不然, 则对任意f∈Lp(Rn)∩L1(Rn), 有Bf∈Fp(Cn)⊂F2(Cn), 这意味着‖f‖L2(Rn)=‖B(f)‖F2(Cn)<. 进一步可得Lp(Rn)∩L1(Rn)⊂L2(Rn).矛盾. 故式(7)不成立. 命题3.2设0 证明 对任意有限区间(a,b), 容易找到某个函数f∈Lp[a,b]nL1[a,b]n.从而对任意的(a,b)可以找到函数f∈Lp(Rn) 使得 在z∈Cn上是无意义的. 进而, 对于一般的函数f∈Lp(Rn), 其Bargmann变换是无意义的.证毕. 另一方面, Bargmann变换在Lp(Rn)上是稠定义的. 例如,Lp(Rn)∩L1(Rn)在Lp(Rn)中是稠密的, 且对于f∈Lp(Rn)∩L1(Rn),Bf是有定义的整函数. 结合引理3.1可知, 当0 定理3.3若1≤p<2, 则算子B:Lp(Rn)→Fq(Cn)是有界的, 并且映射B是单射但不是满射, 其中1/p+1/q=1. 证明 由式(3),B将L1(Rn)有界地映射到F(Cn). 再由引理2.3, 利用复内插可知B:Lp(Rn)→Fq(Cn)是有界的, 其中1≤p<2. 假设Bf=0, 则可证f=0几乎处处成立. 因此算子B:Lp(Rn)→Fq(Cn)是单射. 根据Fock空间的包含关系可知B:Lp(Rn)→Fq(Cn)不是满射.证毕. 以上证明方法适用于p的其他取值情况, 详细证明过程可见定理3.4. 下面给出有界性的另一种证明.当1 则 其中 当p=1,f∈L1(R)时, 有 再次根据式(6)以及 Hausdorff-Young 定理得 定理3.4假设1≤p<2, 1/p+1/q=1. 则算子B:Lp(Rn)→Fp′(Cn)不是有界的, 其中p′ 证明 设p′ ‖B(f)‖Fp′(Cn)≤K‖f‖Lp(Rn) 对所有f∈Lp(Rn)成立. 设Sp=Lp(Rn)∩L1(Rn)⊂Lp(Rn),fr(x)=f(rx), 其中r∈(1,). 则fr∈Sp, 且有 (8) 另一方面, 由式(6)以及变量替换得 因而有 结合式(8), 我们可以找到另一个正常数K>0, 使得 ≤K‖f‖Lp(Rn) (9) 其中p′ C‖F(f)‖Lp′(Rn) (10) 其中C是某个自然数. 由于f具有紧支撑, 由控制收敛定理[12]得 再结合式(10)和法林引理可得 ‖F(f)‖Lp′(Rn)≤ 结合式(9)知, 存在另一个正常数K, 使得 ‖F(f)‖Lp′(Rn)≤K‖f‖Lp(Rn),f∈Sp. 又由于Fourier变换是Sp到Lp(Rn)的等距映射[6], 推出矛盾. 可见算子B:Lp(Rn)→Fp′(Cn)不是有界的. 定理3.5若1≤p<2, 则 (i) 存在函数f∈Lp(Rn)使得Bf∉Fp(Cn); (ii) 不存在Lp(Rn)上的稠密子空间X,使得‖Bf‖Fp(Cn)≤C‖f‖Lp(Rn)对某个正常数C以及所有f∈X成立. 证明 (i) 因为空间Lp(Rn) 没有自然序关系, 也就是说, 任给定两个不同的0 (ii) 若存在Lp(Rn)上的稠密子空间X及正常数C,使得‖Bf‖Fp(Cn)≤C‖f‖Lp(Rn)对所有f∈X成立. 我们将证明(i)不成立, 从而得出矛盾. 为此, 任给f∈Lp(Rn), 设{fn}⊂X使得‖fn-f‖Lp(Rn)→0. 因为X是子空间, 所以 ‖B(fn)-B(fm)‖Fp(Cn)= ‖B(fn-fm)‖Fp(Cn)≤C‖fn-fm‖Lp(Rn). 因此{Bfn}是Fp(Cn)中的Cauchy序列. 又因为Fp(Cn)是Banach空间, 故存在函g∈Fp(Cn)使得当n→时‖Bfn-g‖Fp(Cn)→0. 从而结合式(3) 和式(5), 可得 |Bfn(z)-Bf(z)|≤ 其中C′是常数. 进而有 limn→Bfn(z)=Bf(z),z∈Cn. 因此,Bf=g∈Fp(Cn). 由f的任意性知(i)是错的, 矛盾. 从而(ii)成立. 定理3.6若2 证明 由引理2.3知B:L2(Rn)→F2(Cn)是有界的.又根据式(4),B是L(Rn) 到F(Cn)的有界映射. 由复插值理论知,对任意2≤p≤,B是Lp(Rn)到Fp(Cn)的有界映射. 为证明B是单射, 假设Bf=0. 则 对zj求偏导数并令z=0得 对所有k≥0成立. 说明f=0几乎处处成立. 注意到证明与p的取值无关. 为证明算子B:Lp(Rn)→Fp(Cn)不是满射, 我们固定某个p′∈(2,p) .取函数f∈Lp′(Rn)Lp(Rn). 由Fock的包含关系, 我们有Bf∈Fp′(Cn)⊂Fp(Cn).如果映射B:Lp(Rn)→Fp(Cn)是满射的, 则存在某个函数g∈Lp(Rn)使得Bg=Bf,或者B(f-g)=0. 综上所述, 我们得到f=g几乎处处成立, 这与f∉Lp(Rn)矛盾.证毕.

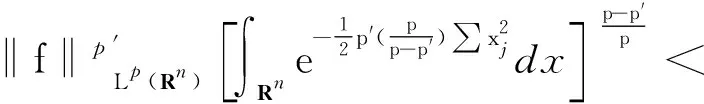
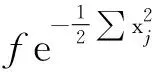
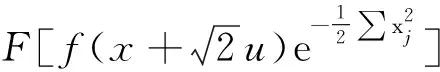
3 主要结果