高集成度小型化共心多尺度光学系统设计

刘 飞，刘佳维，邵晓鹏

(西安电子科技大学 物理与光电工程学院，陕西 西安 710071)

1 引 言

光电成像系统作为最直接的信息获取手段，能提供符合人眼视觉特性的直观探测结果，近年来随着它的发展与应用，人们对光电成像系统的性能提出了更严苛的要求：增大视场以捕捉到大范围内的场景信息，提高分辨率获取空间中重要的细节信息，减小体积提高便携性以适应不同环境的需求。因此，宽视场、高分辨率及小型化的光电成像系统是目前遥感、测绘、环境监控及无人机侦察与防控等领域的迫切需求[1-2]。

传统广域光电成像系统通常采用小视场高分辨率扫描成像方式来增大系统的侦测和监视范围，实现大视场高分辨率成像[3]，然而它存在扫描机构复杂及实时性差的问题，无法对空间信息进行精确判读。相比之下，凝视型成像方式在实时性方面性能更佳，如通过全景鱼眼镜头成像方式[4]和分布式孔径的思想[5-7]来实现大视场成像。由于取消了扫描机构，系统结构大幅简化，体积有效减小，但鱼眼镜头成像方式存在获取的图像几何畸变大、分辨率低及像面照度不均匀的问题，分布式孔径成像系统则存在视场盲区及光能利用率低的缺点，难以实现光电成像装备的实际应用，因此需要研究性能更为优化的新体制凝视型大视场高分辨率成像系统。

在实现大视场高分辨率凝视成像方面，杜克大学Brady等人利用共心球透镜设计了AWARE(The Advanced Wide Field of View Architectures for Image Reconstruction and Exploitation Multiscale Camera)系列相机[8-11]，可同时获得120°的大视场和仅40 μrad的瞬时视场，且能够解决传统凝视型光电成像系统畸变大、光能利用率低及视场盲区等问题，但该系统采用二次成像方式从而导致系统结构长、体积大，故难以满足小型化、轻量化的要求。针对以上问题，本文设计了高集成度小型化共心多尺度光学系统，该系统不仅可以有效实现大视场高分辨率成像，同时具有结构简单、集成度高、体积小等特点。

高集成度小型化共心多尺度光学成像系统充分利用了球透镜视场大、光能收集能力强、轴外像差小等特点，将共心球透镜作为主物镜，并采用伽利略型多尺度成像结构，将球透镜与小相机阵列进行级联，以更紧凑的系统结构获取大视场高分辨率成像效果。此外，通过研究共心球透镜结构复杂度与其成像性能的关系，从而确定一个最优化的系统结构，可在提高成像性能的前提下进一步降低系统结构的复杂度。设计结果表明，该系统成像效果优良，并具有良好的成像稳定性。

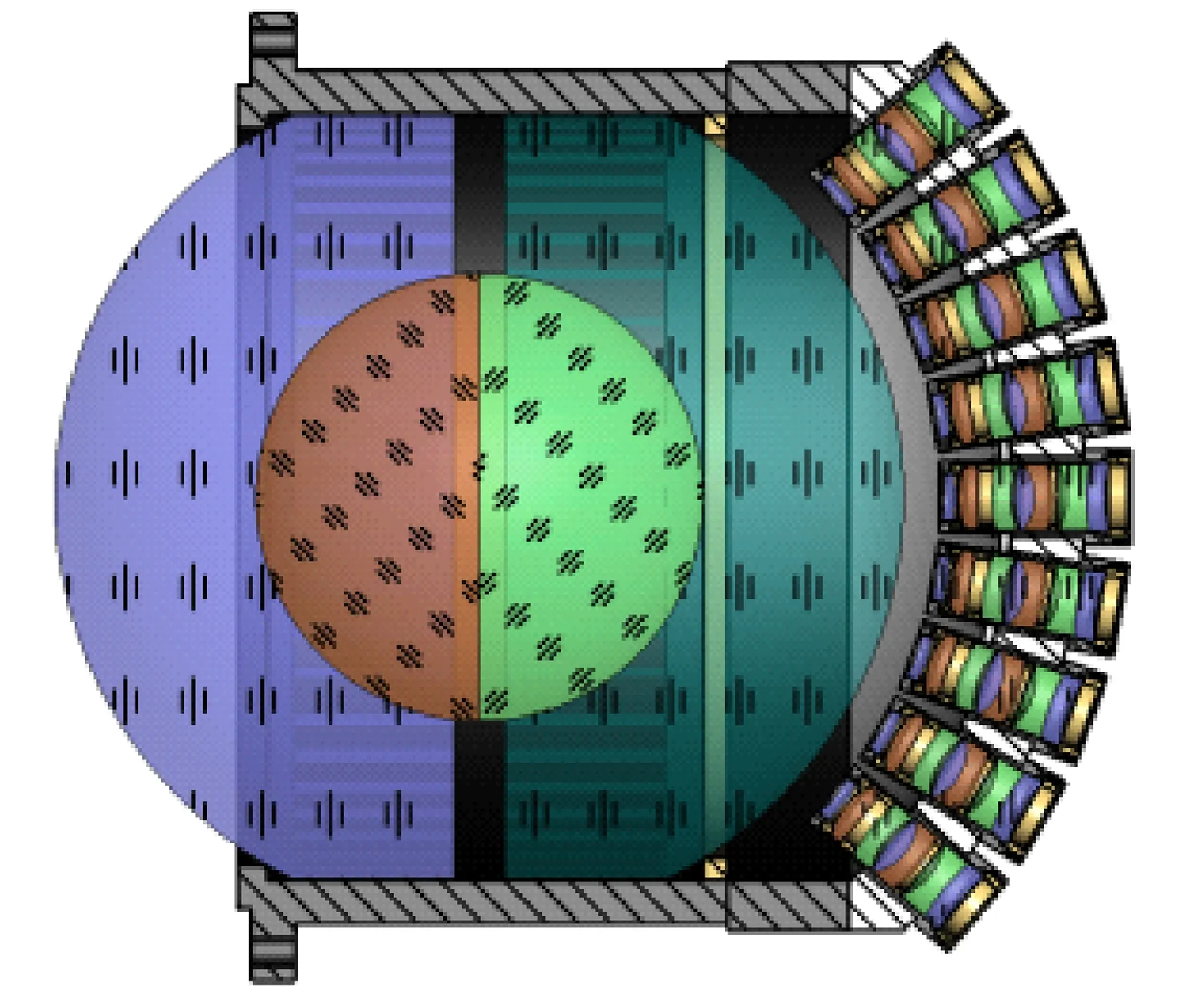
图1 共心多尺度光学成像系统原理Fig.1 Schematic diagram of concentric multiscale optical imaging system

2 成像原理

高集成度小型化共心多尺度光学成像系统是一个多尺度成像系统，由主物镜与次级小相机阵列组成。其中，主物镜为一个共心胶合球透镜，如图1所示，它具有旋转对称的特点，没有传统意义上的主光轴，因此与视场相关的像差较小，能够实现大视场成像和高效率能量收集；次级相机阵列排布于球透镜后一定距离处，用于分割大成像视场，同时其若干个子像面之间存在视场重叠，通过图像拼接可获取完整的目标场景信息。此外，次级成像系统还能够进一步校正主物镜的残留像差，解决传统单口径成像系统视场与分辨率相互制约，难以同时实现大视场、高分辨率成像的问题。

共心多尺度成像结构根据有无中间像面可分为开普勒型与伽利略型[12-13]，图2所示为两者的结构示意图。在相同的光学参数条件下，伽利略式相比开普勒式可获得更紧凑的系统结构，并且长度近似为开普勒形式的一半，因此采用伽利略方式能够在实现大视场高分辨率成像的同时保证系统具有体积小、轻量化的结构特点。

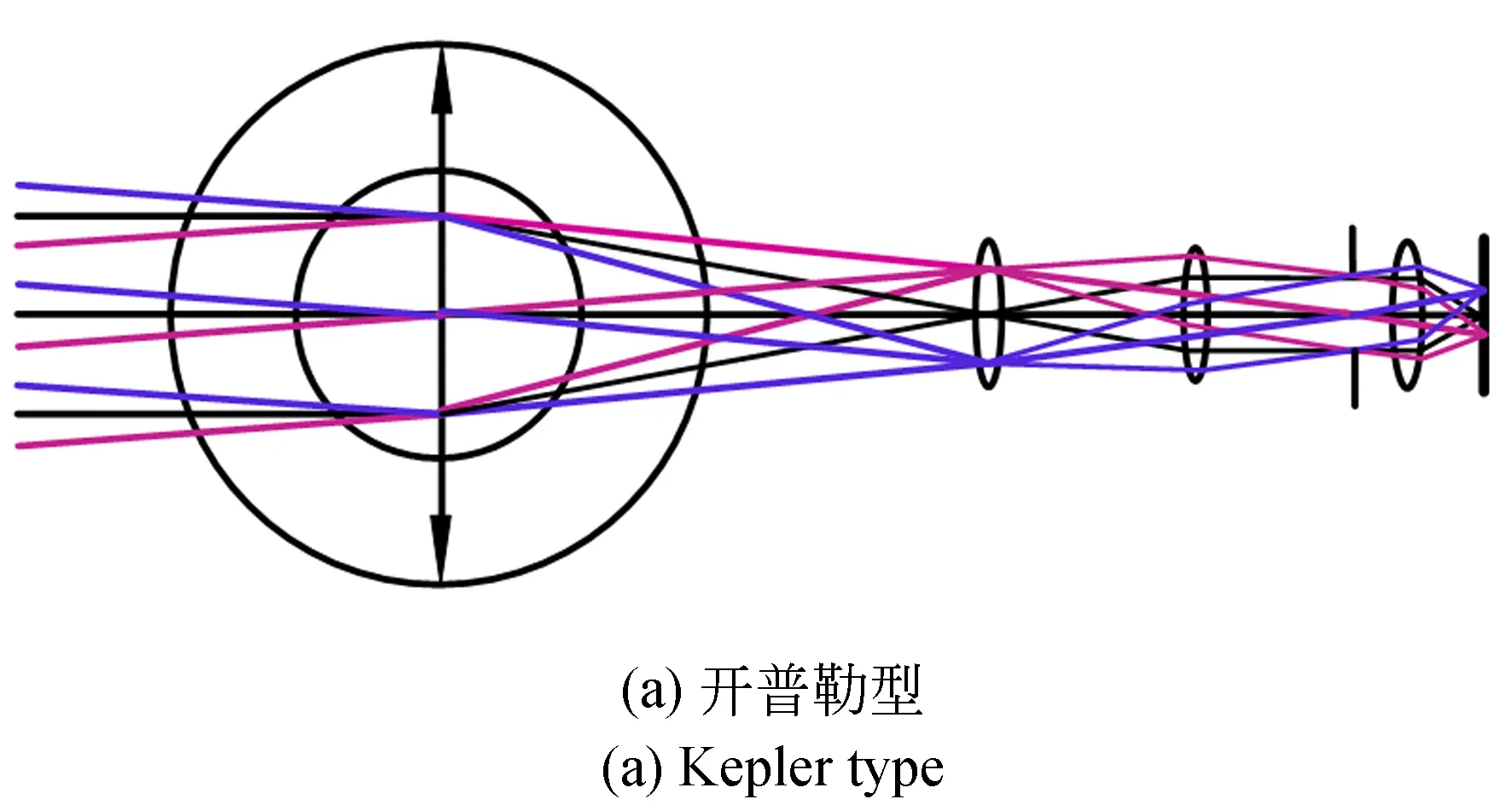
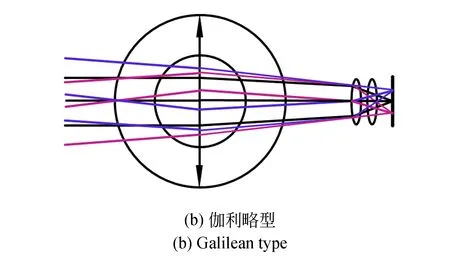
图2 共心多尺度系统示意图Fig.2 Schematic diagram of concentric multi-scale system

共心球透镜作为系统的主要组成部分，在设计中需要在其结构复杂度与成像性能之间进行权衡，图3给出了不同复杂度下的共心球透镜结构及其调制传递函数MTF曲线。在共心结构特点下，球透镜在复杂化的过程中每增加一片透镜仅增加一个玻璃材料、一个曲率半径及一个玻璃厚度的设计变量，因此优化中便于控制变量以进行成像性能的比较，图中所示系列透镜均是最优化后F/2.5，70 mm的共心球透镜。分析图3中MTF曲线可以得出，随着表面数量的增加，MTF随之提高，但通过增加系统的复杂度来提高成像性能时存在一个效果递减定律，即结构复杂度由一个表面增加至两个表面时，MTF值在频率200 lp/mm处由0.02提升至0.4，提高了约20倍，而复杂度由2个表面增加至6个表面时，MTF仅提升至0.5，提高了0.25倍。而图3上方系列透镜的结构图则说明，随着复杂度的提高，球透镜的口径随之增加，此外，通过比较透镜(2)、(3)与透镜(4)、(6)可知，在透镜层数相同的情况下，具有完全对称结构的共心球透镜更易获得较小的口径尺寸。通过上述分析可找出一个最优化的设计，在该设计下系统不仅具有良好的成像性能，同时有较小的尺寸和低复杂度。

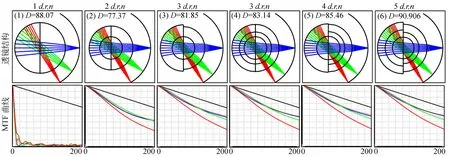
图3 不同复杂度下的共心球透镜系统及其调制传递函数曲线Fig.3 Concentric spherical lens with different complexity and their modulation transfer function curves

3 共心多尺度光学系统设计

系统的成像波段范围为可见光波段，系统焦距为40 mm，成像选用索尼IMX226探测器，像元数量为4 000(H)×3 000(V)，像元尺寸为1.85 μm，综合考虑像差校正难度及相机阵列拼接时对相机口径的限制，F数取3.3。通过次级相机阵列拼接，系统可以捕捉到一个近乎半球形视场的场景信息。

3.1 主物镜设计

基于上述对共心球透镜结构复杂度与其系统性能的研究分析可知，具有完全对称结构的双层共心球透镜可在低结构复杂度及小尺寸下获得优良的成像效果，因此本文采用完全对称结构的双层共心胶合球透镜作为系统的主物镜。在该结构下，共心球透镜以其固有的旋转对称性，使过球心的每一条光线都可视为主光轴，因此仅存在轴上像差(轴上球差与色差)以及较小的轴外像差，此外，利用胶合透镜可以校正球差，根据不同材料的色散特性对玻璃材料进行组合可进一步补偿色差[14-15]。在实际设计中，由于共心球透镜各个面共用一个曲率中心，故仅需确定第一面的曲率半径，其他表面的曲率类型设置为共心曲率即可。结合上述像差平衡理论在光学设计软件ZEMAX中对球透镜进行优化可获得像差校正良好的主物镜结构，优化后的共心球透镜结构如图4所示。

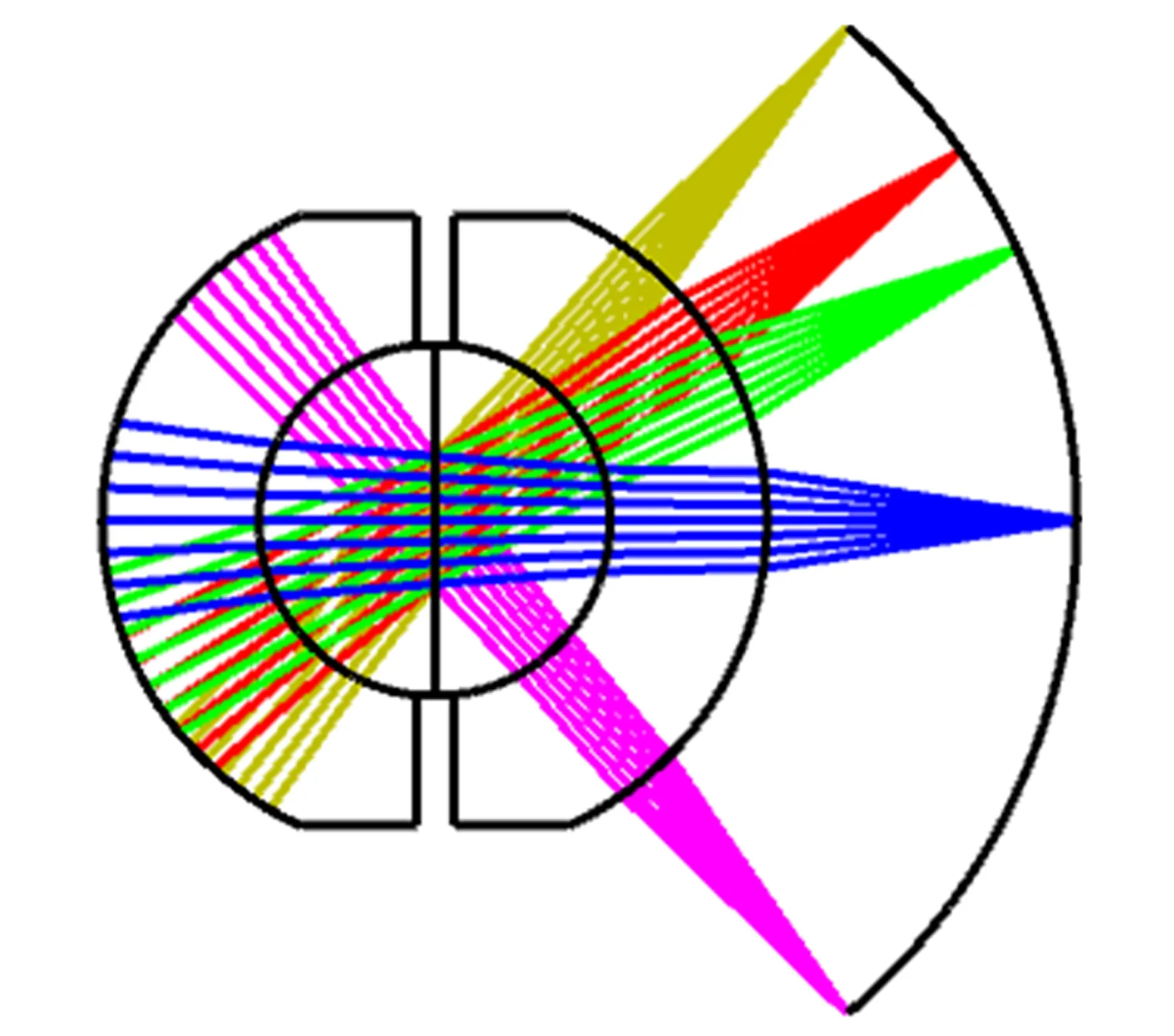
图4 优化后的共心球透镜结构Fig.4 Optimized structure of concentric spherical lens

该共心球透镜的调制传递函数曲线(Modulation Transfer Function,MTF)如图5(a)所示，在特征频率270 lp/mm处，全视场范围的MTF值可达0.2，且MTF曲线平直趋势一致，说明各视场的成像质量一致性好，从而可用相同的小相机校正不同视场处的残余像差。优化后的点列图如图5(b)所示，各个视场弥散斑80%的能量均在艾里斑内，表明共心球透镜具有较好的能量收集能力，可在像面上获得均匀的照度。上述数据表明，文中所设计的双层共心球透镜具有光学结构简单，与视场相关的像差小，成像质量良好的特点。

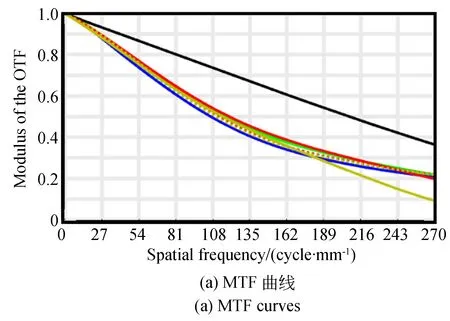
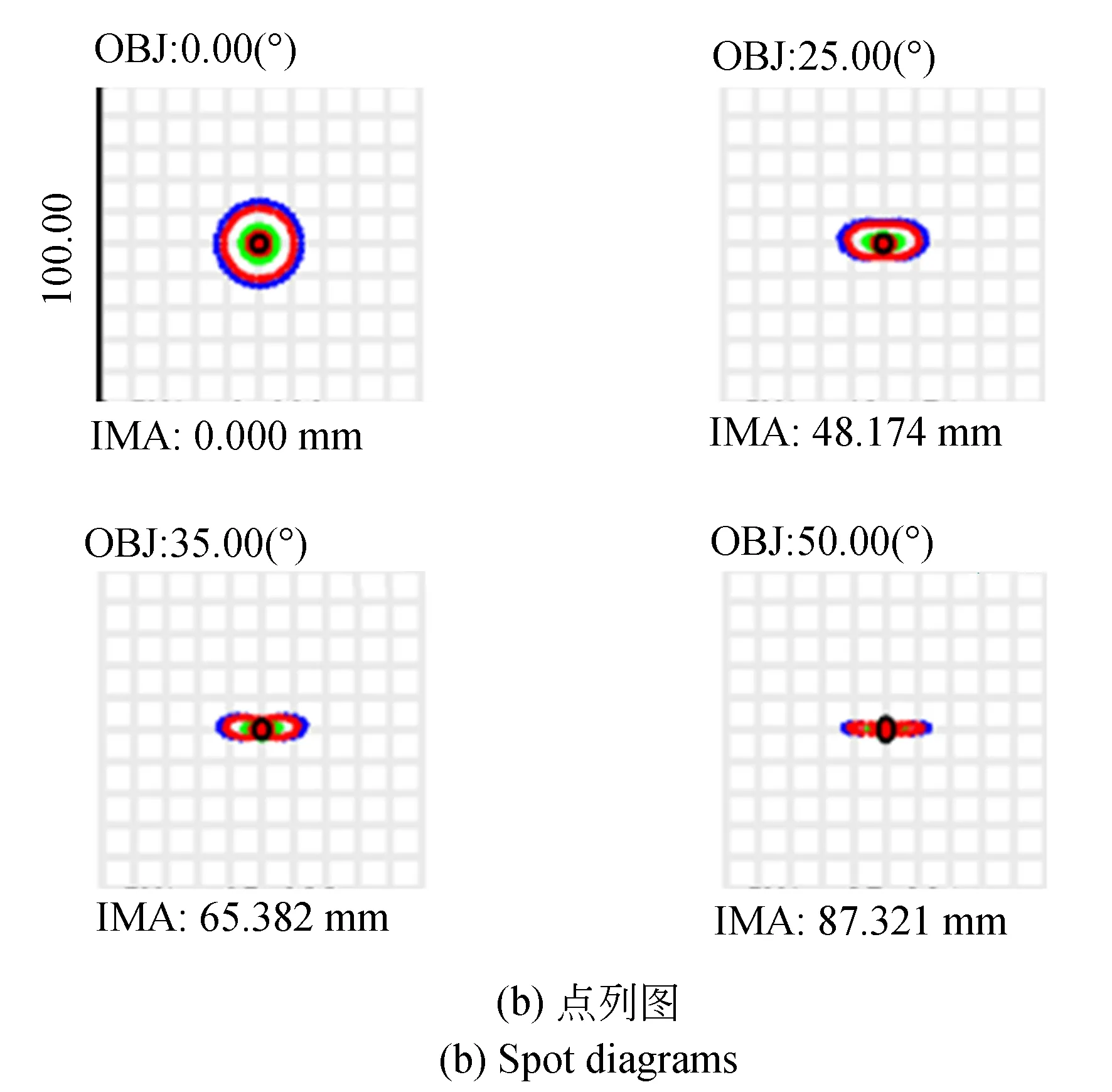
图5 共心球透镜优化后的成像评价Fig.5 Image evaluation of designed concentric sphere lens

以近轴光线追迹的形式计算标准球面的Seidel像差系数可以评价光学系统成像质量，结果如表1所示。其中，影响传统光学系统成像质量的彗差、像散、畸变及垂轴色差均等于0，可见该共心球透镜不存在与视场相关的像差；此外，球差与轴向色差作为轴上像差可利用次级成像系统进行进一步校正；针对球透镜固有的Petzval场曲，通过设定按特定规则排布于球透镜附近的次级相机阵列的方式，减小它对成像质量的影响。

表1 共心球透镜Seidel像差系数

Tab.1 Seidel aberration coefficients of concentric spherical lens

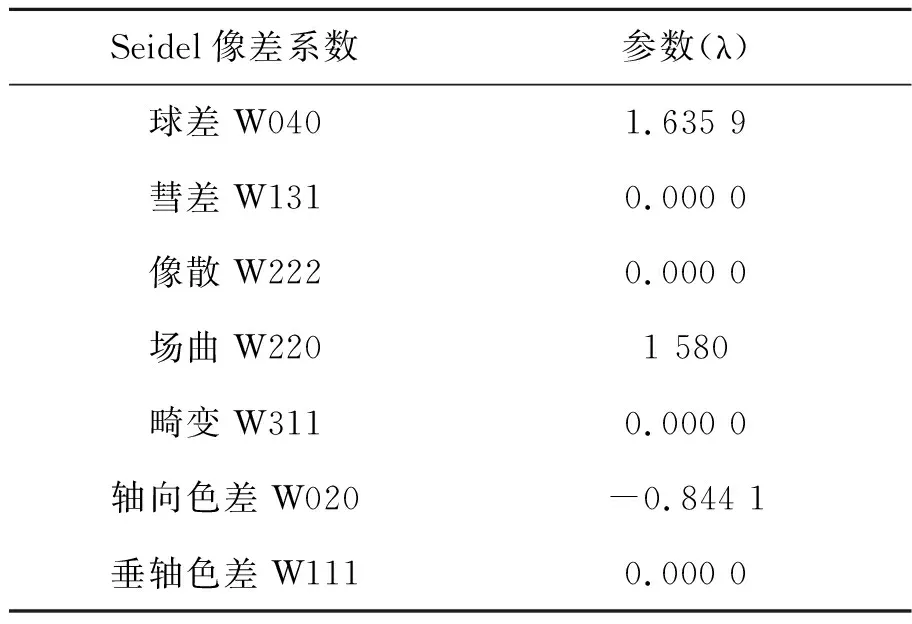
Seidel像差系数参数(λ)球差W0401.635 9彗差W1310.000 0像散W2220.000 0场曲W2201 580畸变W3110.000 0轴向色差W020-0.844 1垂轴色差W1110.000 0

3.3 次级小相机及整体系统优化

小相机阵列作为次级成像系统分割球透镜的大视场并将其转接并形成若干个视场存在重叠的子图像，最后通过对子图像进行拼接获取大视场高分辨率成像效果。除分割视场外，次级相机阵列还需要考虑校正主物镜的残留像差。由于球透镜固有的Petzval场曲，导致像平面的中心位置与边缘位置模糊程度不一，利用现有的平面探测器无法解决，因此通过设计按特定规则排布的相机阵列，将它排布于距球透镜一定位置处并与其共心的球形包络面上，来减小场曲对成像质量的影响[16]。

此外，次级成像系统的口径、视场、焦距及次级成像系统至球透镜中心的距离等均是影响像面拼接的制约条件，因此需在相机阵列设计时考虑系统像差的校正与视场重叠的问题。为保证相邻相机间的视场重叠并提高视场利用率，同时使平面矩形探测器的排布更加紧密，故采用六边形相机阵列排布方式，各镜头像方视场的重叠情况如图6所示。考虑到后期视场拼接的需要，相邻相机须至少存在5%的重叠率，因此在本文所述系统的相机阵列排布设计中，使横向排布的相邻相机与球透镜中心所张开的夹角为10°，纵向为7.5°，计算可得横向视场重叠率为5.4%，纵向视场重叠率为5.54%。

图6 六边形排布视场拼接示意图Fig.6 Field of view mosaic diagram in hexagonal array

已知所需全视场θtotal、相邻相机轴线间的夹角θvalid及单个子系统视场θsub，则有：

(n-1)θvalid+θsub≥θtotal.

(1)

为实现全视场拼接成像，系统所需总相机个数N由式(2)给出：

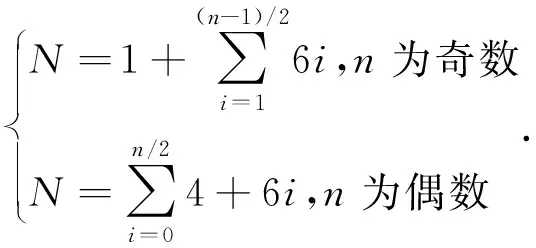
(2)

在本文设计中，采用61个相机阵列进行多尺度拼接最终实现90.57°×67.94°的大成像视场。为保证相机封装后互不干涉且不增加结构设计的难度，因此要求相机的封装口径D满足：

D≤2Lsin(θvalid/2)-4，

(3)

其中L表示相机到球透镜中心的距离。

图7所示为相同视场重叠率下六边形排布与矩形排布对比图。由图可知，在有效视场相同的条件下，六边形排布方式所用相机数量更少，排布更紧密。

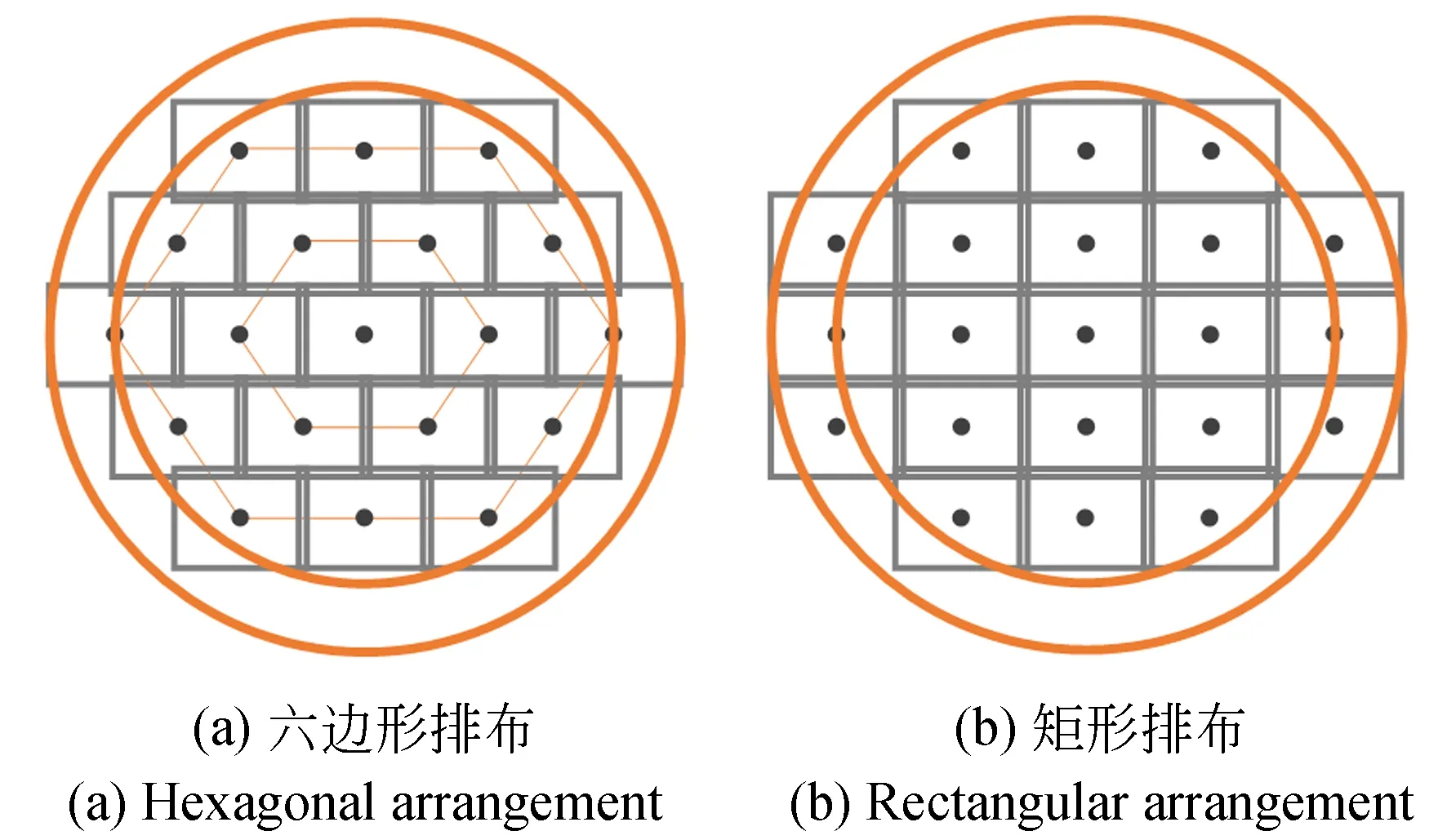
图7 六边形排布与矩形排布对比Fig.7 Comparison between hexagonal layout and rectangular layout

结合上述约束条件设计并优化光学系统，此外，由于共心球透镜结构对称、无固定光轴，每个次级成像系统都可看作与共心光学主物镜共轴成像，因此次级小相机阵列可采取相同的光学结构，故只需设计中心视场的次级成像系统即可，可大大简化设计过程。图8所示为系统优化后的结构。

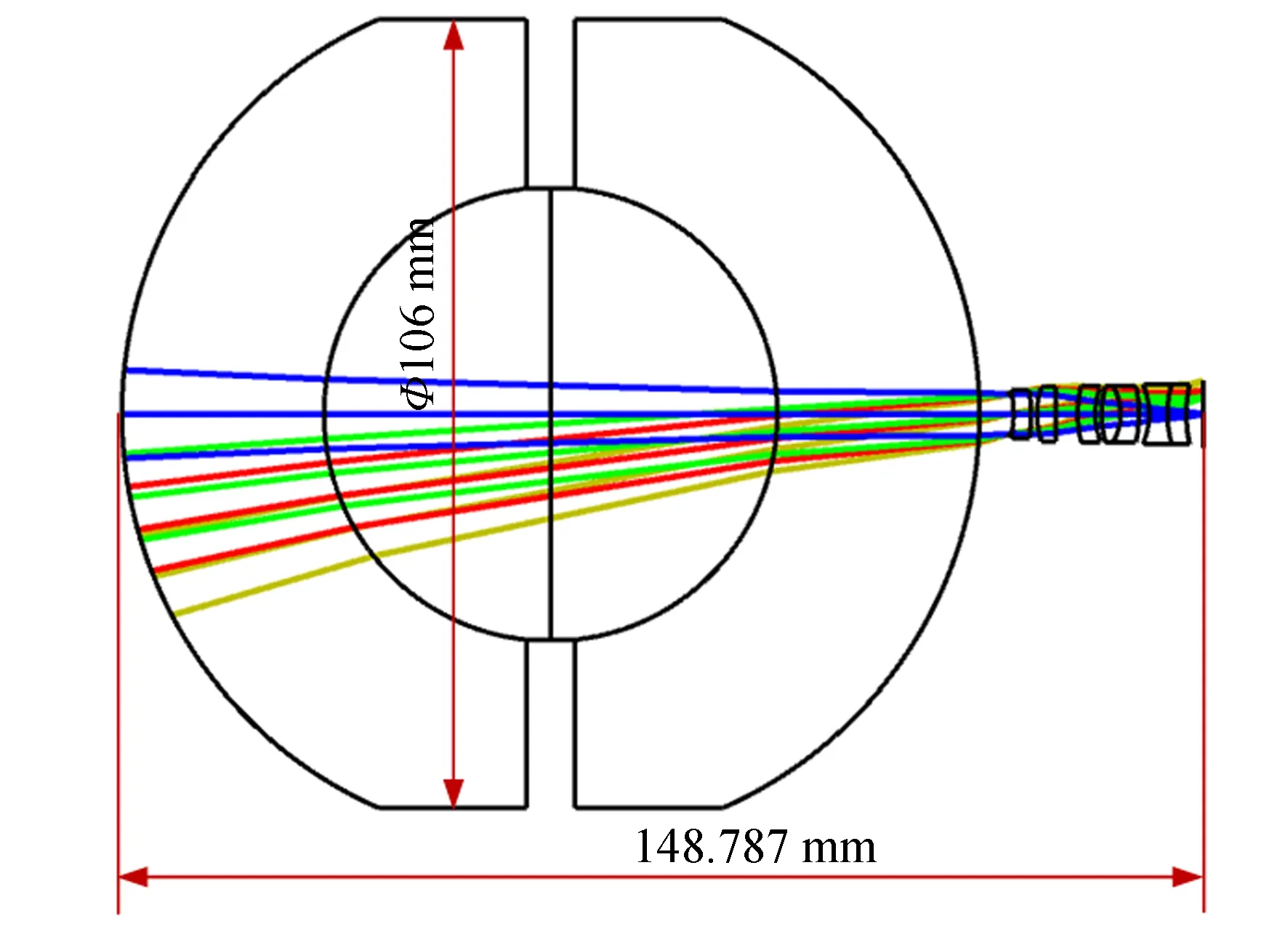
图8 光学系统结构Fig.8 Optical system structure

系统的MTF曲线、点列图及场曲畸变如图9所示。图9(a)表明，该系统在特征频率270 lp/mm处，系统的MTF值在0.3左右，全视场的传递函数曲线趋势一致且均接近衍射极限，说明各视场成像质量良好。图9(b)所示的点列图中，系统全波段弥散斑均方根(Root Mean Square,RMS)半径最大值为1.398 μm，小于探测器的像元尺寸1.85 μm，满足系统与探测器的匹配要求。图9(c)为系统的场曲畸变情况，场曲在0.03 mm以内，畸变<±0.3%，两者均控制在有效范围内，满足成像指标要求。上述分析表明，高集成度小型化共心多尺度光学成像系统各参数均满足设计要求，成像效果良好。

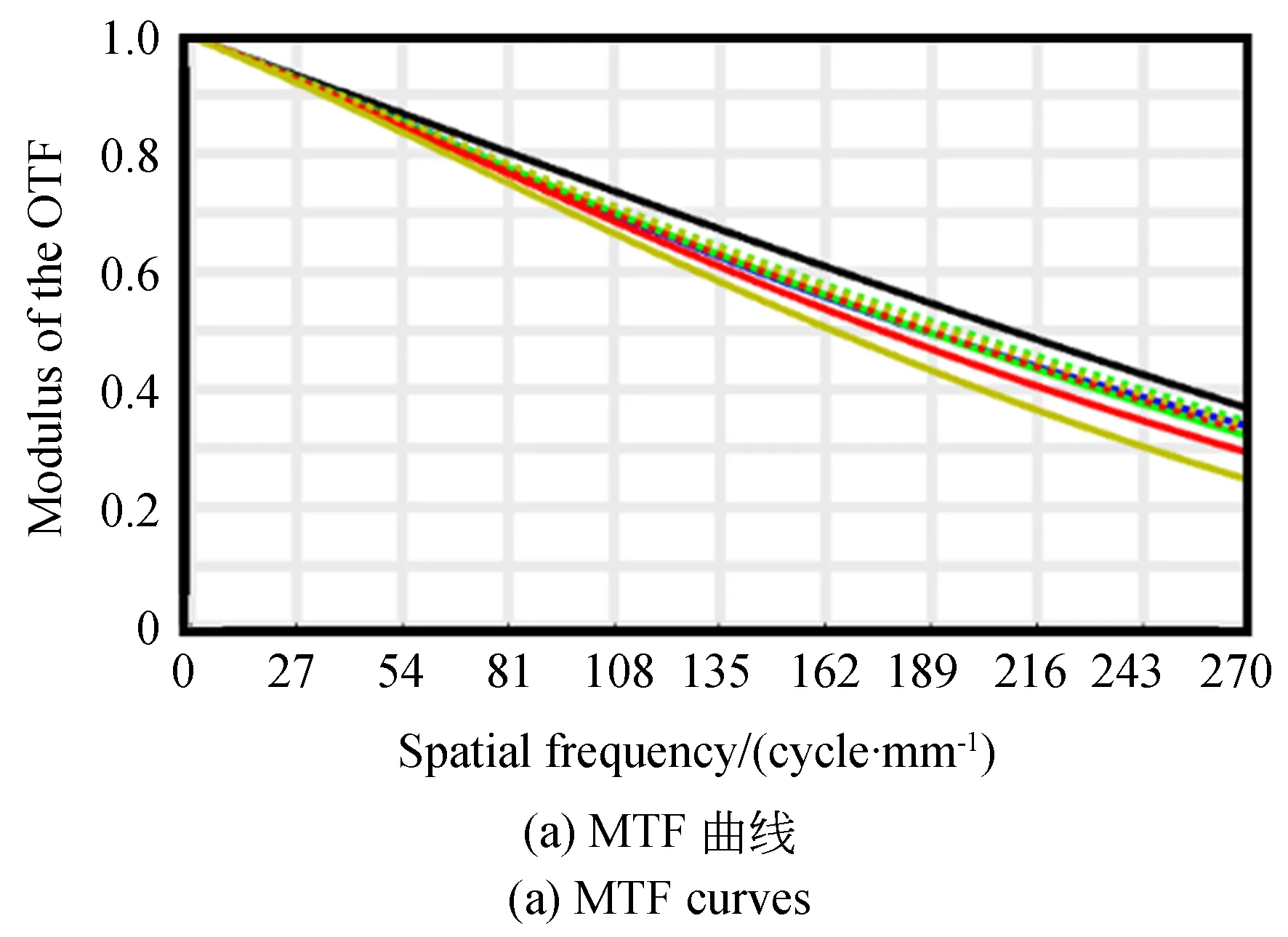
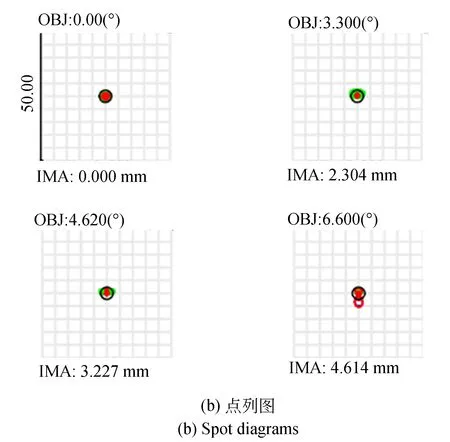
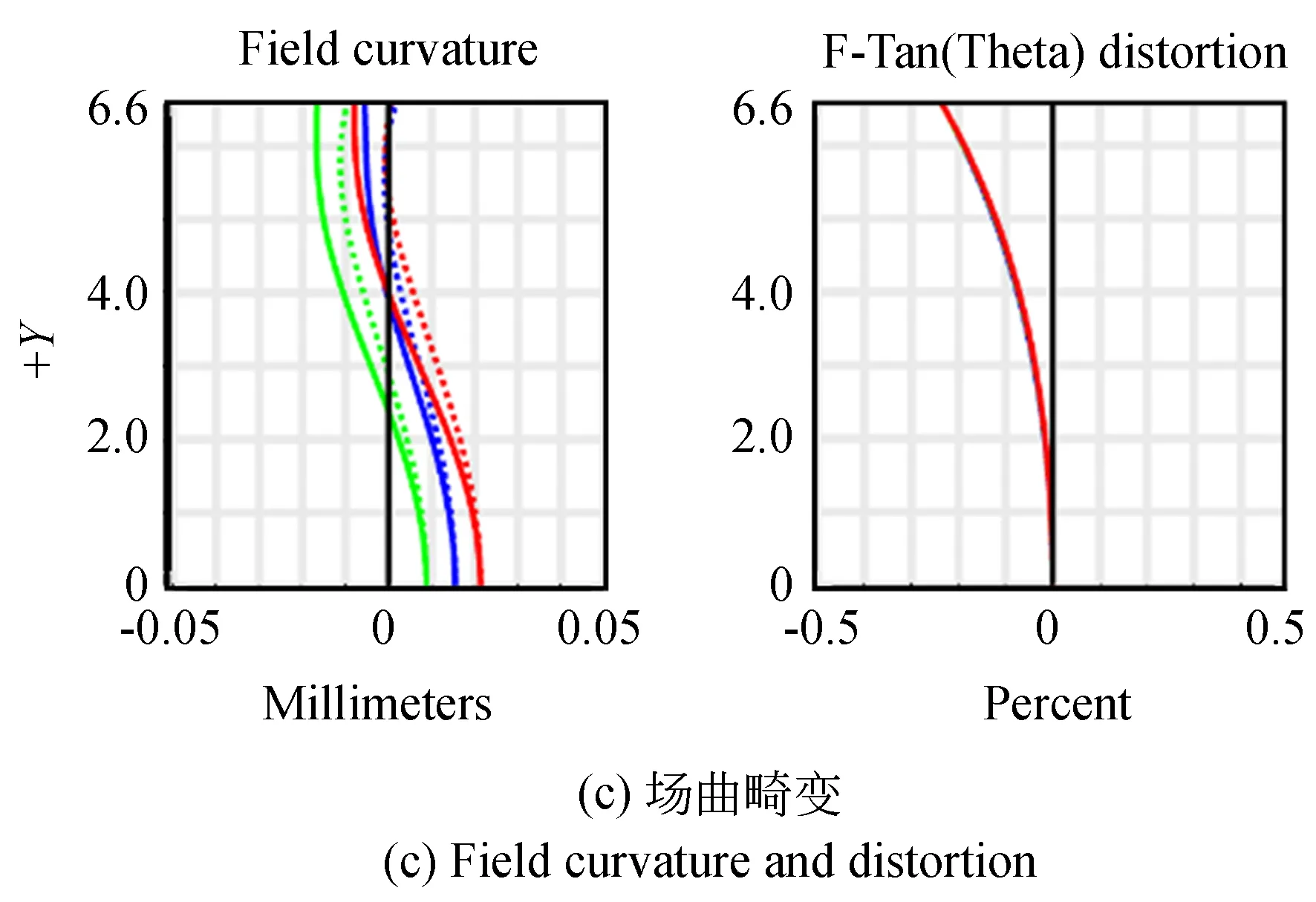
图9 系统成像评价图Fig.9 The imaging evaluation diagram of the system

4 系统公差分析

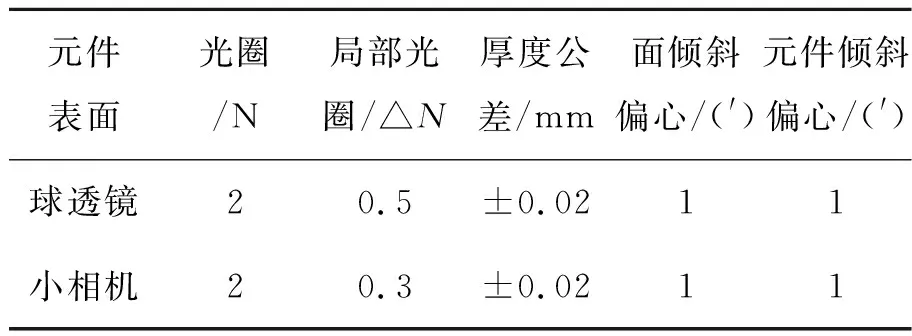
在光学设计完成后，为避免光学系统在加工、装配时由于公差分配不合理而导致的成像性能下降的问题，本文利用敏感度分析法对伽利略型共心多尺度光学成像系统的成像稳定性进行分析，并为它制定合理的公差分配，确保光学系统的成像质量能够达到要求[17]。表2所示为经过公差分析计算后各元件允许的公差限，并且表中所有的公差容限在实际加工及装配中均可实现。

在表2所示的公差容限下，对该系统执行10 000次蒙特卡洛分析，分析结果如表3所示。统计数据表明，系统在特征频率270 lp/mm处预估MTF值为0.193 3，其中MTF值大于0.156 8的概率可达90%，表明系统在给定的公差限内具有良好的成像质量。

表2 系统各元件所允许的公差限

Tab.2 Tolerance limit for each element of concentric multiscale system

元件表面光圈/N局部光圈/△N厚度公差/mm面倾斜偏心/(')元件倾斜偏心/(')球透镜20.5±0.0211小相机20.3±0.0211

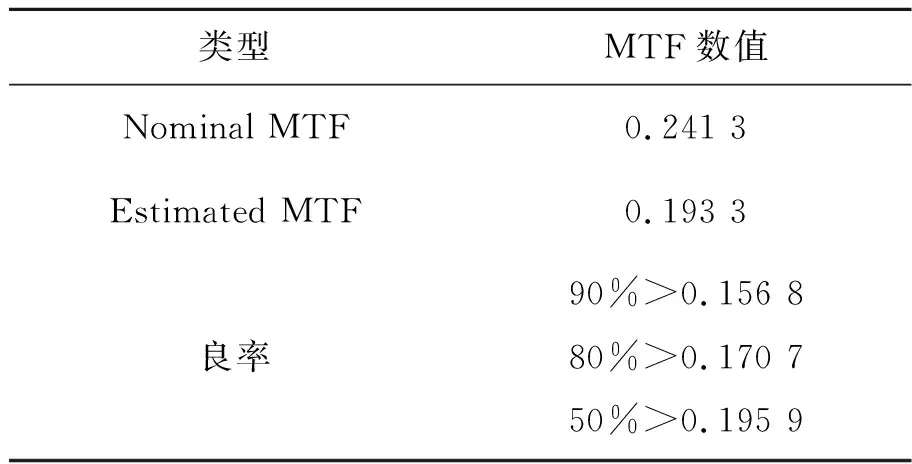
表3 公差分析统计结果

5 结 论

本文针对目前光电成像系统对于大视场、高分辨率实时成像探测的需求，提出一种高集成度小型化共心多尺度光学成像系统。该系统利用双层共心球透镜有效减小了与视场相关的像差，并结合基于球形分布的次级相机阵列的设计有效消除了残余像差，此外系统采用伽利略型多尺度成像方式将主物镜与次级相机阵列进行级联，获得更紧凑的体积结构，并通过六边形几何排布方式减少相机使用数量，从而使系统进一步满足小型化与轻量化的设计要求。该系统在全视场范围内的传递函数曲线趋势一致且接近衍射极限，在特征频率270 lp/mm处的MTF值可达0.3；全波段弥散斑RMS半径的最大值为1.398 μm，小于探测器像元尺寸；场曲在0.03 mm以内，畸变小于±0.3%。设计结果表明，该共心多尺度光学成像系统结构简单，成像效果优良。由于共心球透镜的理论视场可达近180°，在此基础上可根据需求调整次级相机的数量，从而增大或减小有效视场，具有很高的工程应用价值。