载机飞行参数对倾斜成像重叠率影响及补偿

李 军，黄厚田，修吉宏，李 彬，张 赫

(1. 中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2. 中国科学院 航空光学成像与测量重点实验室，吉林 长春 130033)

1 引 言

航空成像具备机动性强、特定地区重访周期高的优势，在情报获取、减灾救援、农业调查等方面均有广泛应用[1]。为了扩大成像范围并能在边境线附近对邻国的军事目标进行侦察，侦察相机通常采用大斜视摆扫成像工作方式[2-3]。大斜视成像相机一般焦距较长，视场角较小，分析并抑制载机飞行参数影响并进行补偿是大斜视航空成像需要解决的一个重要问题。

杨秀彬、王亚敏等在垂轨凝视搜索成像分析[4-5]中简单介绍了凝视成像的的重叠率结果，并未详细给出重叠率分析过程，且所指重叠率为凝视地区图像重叠情况，与航空相机中的重叠率含义有所不同。周刚等在航空相机扫描角研究中仅分析了扫描角对重叠率影响，未涉及载机参数方面研究[6]。万磊等在飞行器姿态对航空相机影响中未研究重叠率问题[7]。

本文在乔川等给出的大倾斜成像航空相机对地目标定位[8]的基础上给出了基于坐标变换的重叠率计算方法；针对载机的航向角、俯仰角、横滚角、飞行速度变化、飞行高度变化等参数单变量影响，通过几何方法进行分析，并给出了与坐标变换方法的对比结果；针对同时存在航向角、俯仰角、横滚角影响的情况，给出了基于坐标变化方法的重叠率影响结果及对应的相机位角、俯角的补偿量；基于载机飞行速度和航高的影响，给出了调整拍照周期的补偿方法。

2 基于坐标变换的重叠率计算

2.1 重叠率定义

航空相机结构如图1所示[8]，相机安装在飞机上相机，相机位角轴对应内框架转轴，相机俯角轴对应外框架转轴，俯角轴与载机横滚轴一致，初始时内框架转轴与载机俯仰轴平行，在成像过程中可调节相机位角轴和俯角轴控制相机视轴指向。

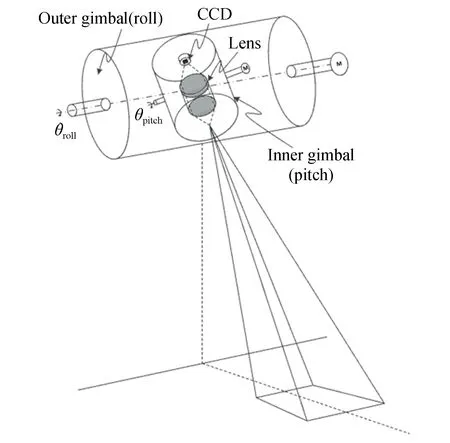
图1 航空相机结构示意图Fig.1 Diagram of aerial camera structure

随飞机飞行相机在图2中A，B点进行扫描成像，要求相邻两个条带图像具有一定的重叠区域，如阴影区域所示。对倾斜成像而言，条带图像中靠近机下点的一端图像定义为近地点图像。图像重叠率随着相机倾斜角变大逐渐增加，近地点图像重叠率最小。因此，本文讨论近地点图像的重叠率。

在飞机姿态角较小时，单幅图像飞行方向覆盖长度为：

(1)

其中：He为飞机相对目标点的高度，θ为相机俯角与地面垂直方向夹角，ω为相机飞行方向的视场角。

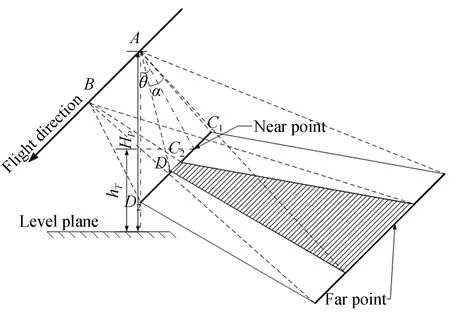
图2 飞行方向重叠率示意图Fig.2 Overlap of flight direction

相邻条带载机步进距离C1C2=Lstep，相邻条带图像重叠区C2D1=Lsingle-Lstep重叠率表达式为：

(2)

2.2 坐标系建立

大倾斜远距离成像无法使用激光测距进行目标定位[9]，先采用直接地理定位方法确定目标位置[8,10-11]，再将目标换算到平面直角坐标系下进行重叠率分析。文中涉及到的坐标系包括建立分析所需的地心直角坐标系(Earth-Centered,Earth-Fixed,ECEF)、地理坐标系(North East Down,NED)、载机坐标系系(AC)、相机坐标系(S)、高斯-克吕格坐标系。其中文献[8]给出了除高斯-克吕格坐标系外的其他坐标系间转换关系的推导过程，此处只引用其主要结论。

相机坐标系定义——相机俯角轴定义为XS轴，指向相机头方向为正，位角轴定义为YS轴，指向相机右侧为正，ZS轴指向相机视轴向下方向为正。其中相机俯角为θ，位角转角为φ，当θ，φ为零时，相机坐标系与飞机坐标系完全重合。飞机坐标系到相机坐标系的转换公式为:

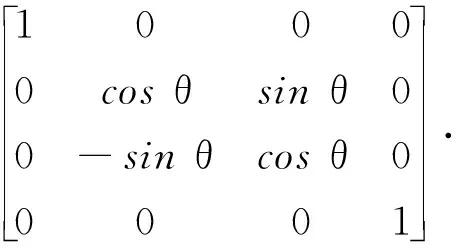
(3)

飞机坐标系定义——横滚轴定义为XAC轴，指向飞机头方向为正，俯仰轴轴定义为YACY轴，指向飞机右侧为正，ZAC轴向下方向为正。飞机横滚角为α、俯仰角为β、航向角为λ，飞机地理坐标系到飞机坐标系的转换公式为:

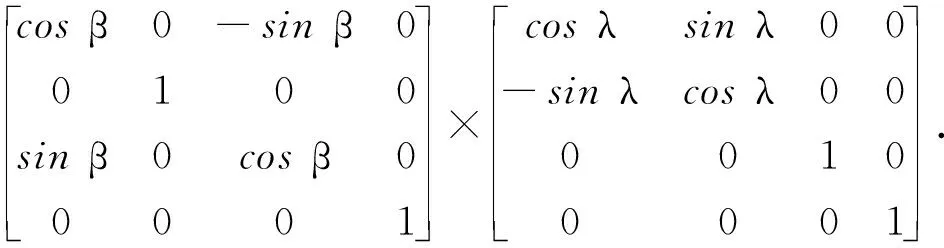
(4)

地心直角坐标系——为原点处于地球质心，XECEF轴指向本初子午线与赤道的交点，ZECEF轴指向地理北极，YECEF轴与其他两轴组成右手坐标系。WGS-84标准定义的地球椭球模型[6]在地心直角坐标系下可表述为:

(5)

其中：RE为地球长半轴，RP为地球短半轴。

大地坐标系采用WGS84标准，目标的纬度为B，经度为L，大地高位H，大地坐标系到飞机地理坐标系的转换公式为:

(6)

其中:目标经度为L，纬度为B和大地高信息为H，地球椭球第一偏心率为e1，目标对应卯酉圈的曲率半径为RN。

大地坐标系到地心直角坐标系坐标变换公式为:

(7)

地心直角坐标系到大地坐标系坐标变换迭代公式(8)所示:

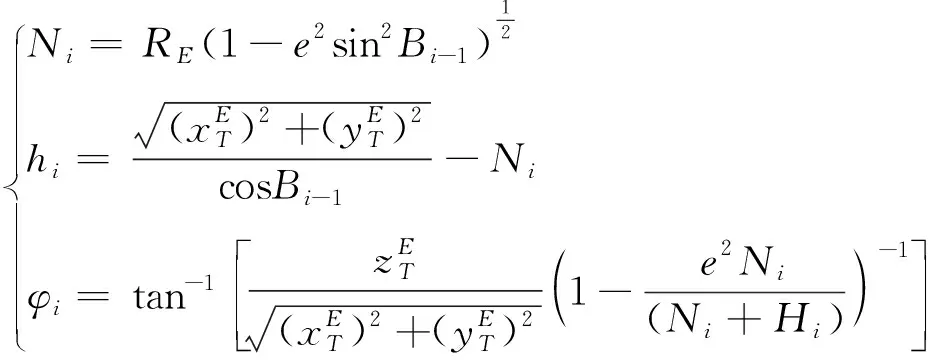
(8)

目标经度信息由式(9)给出:

(9)

高斯克吕格坐标[12]——以中央经线为纵轴(XGK轴)，赤道为横轴(YGK轴)，两轴相交为原点。已知大地纬度B、经度L，则高斯-克吕格投影公式[13]为:

x=Xc+RNtcos2Bl2[0.5+

y=RNcosBl[1+

t4+14η2-58t2η2)cos4Bl4]

其中：XC为中央子午线弧长，RN为卯酉圈曲率半径，t=tanB,η2=e22cos2B，e2为地球椭球第二偏心率，B为当地纬度，l为当地经度与中央子午线经度差(单位为弧度)。中央子午线长度计算公式为:

X=RE(1-e2)(A1B-A1sin(2B)+

C1sin(4B)-D1sin(6B)+E1sin(8B)-

F1sin(10B)+G1sin(12B))，

(11)

公式中系数为:

(12)

其中：e1为地球椭球第一偏心率，RE为地球椭球长半轴；在中国区内，为了避免出现负数，可在y方向加上500 000 m。

2.3 重叠率计算过程

目标在探测器上投影点在相机坐标系下的坐标为:

(13)

其中：a为探测器像元尺寸，M为探测器沿飞行方向总像元数，N为垂直飞行方向总像元数，(i，j)为目标在探测器上像元数坐标。

(14)

和地球椭球方程:

(15)

在高斯-克吕格坐标系下，前一条带近地点中心点坐标为(x1np_c,y1np_c)，后一条带中心点坐标为(x2np_c,y2np_c)，则相邻条带步进距离为:

(16)

利用公式(2)，可计算出重叠率。

综合上述分析，重叠率计算过程如图3所示。

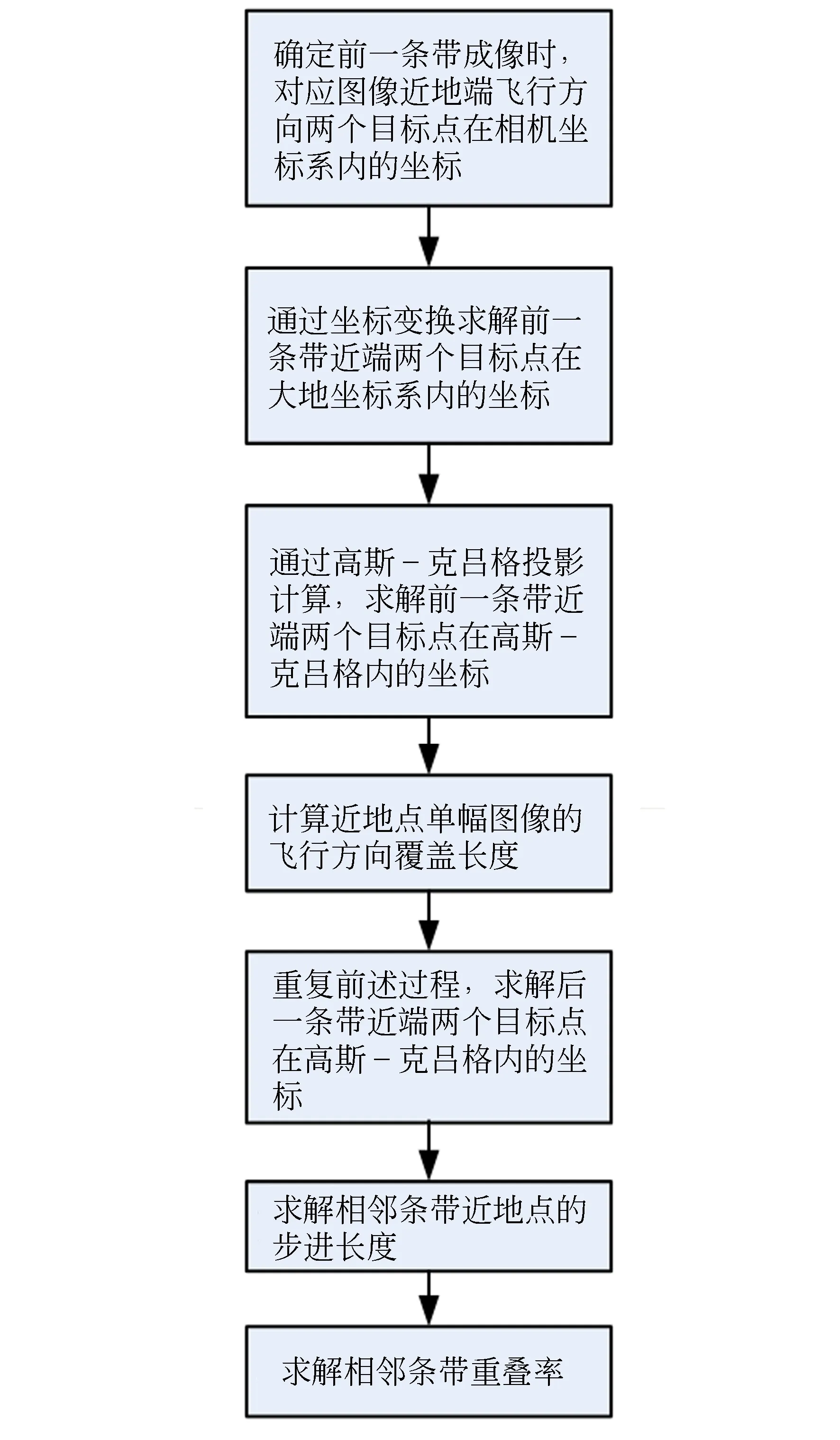
图3 重叠率计算流程Fig.3 Flow chart of overlap calculation

3 重叠率影响及补偿

3.1 飞机姿态角的影响及补偿

首先分析仅存在飞机航向角变化对重叠率的影响。图4中前一条带飞机位于位置P1，对应地面近地端为位置O1，当不存在飞机航向变化时，后一条带图像飞机位于位置P2，对应地面近地端为位置O2。如果飞机在P2位置相对P1位置航向角存在Δλ的波动时，相机视轴位于与航向旋转轴夹角为θ的圆锥面上运动，视轴与地面交点从O2运到位置O3。O5为飞机位置P2在地面投影点，则O5O2与O5O3的夹角也为Δλ。

设飞机相对目标高度为He，则O5O3的长度为LO5O3=Hetanθ，飞机航向变化导致目标点在飞行方向的偏差为:

LO3O4=LO5O3sin Δλ=Hetanθsin Δλ.

(17)

飞机航向变化导致目标点在与飞行垂直方向的偏差为LO4O3=Hetanθ(1-cos Δλ)。

航向变化对重叠率影响公式为:

(18)

从公式(18)中可以看出垂直成像时θ=0°，航向角变化对于重叠率无影响。但对于大倾角成像来说，航向角的变化影响是不可忽略的。

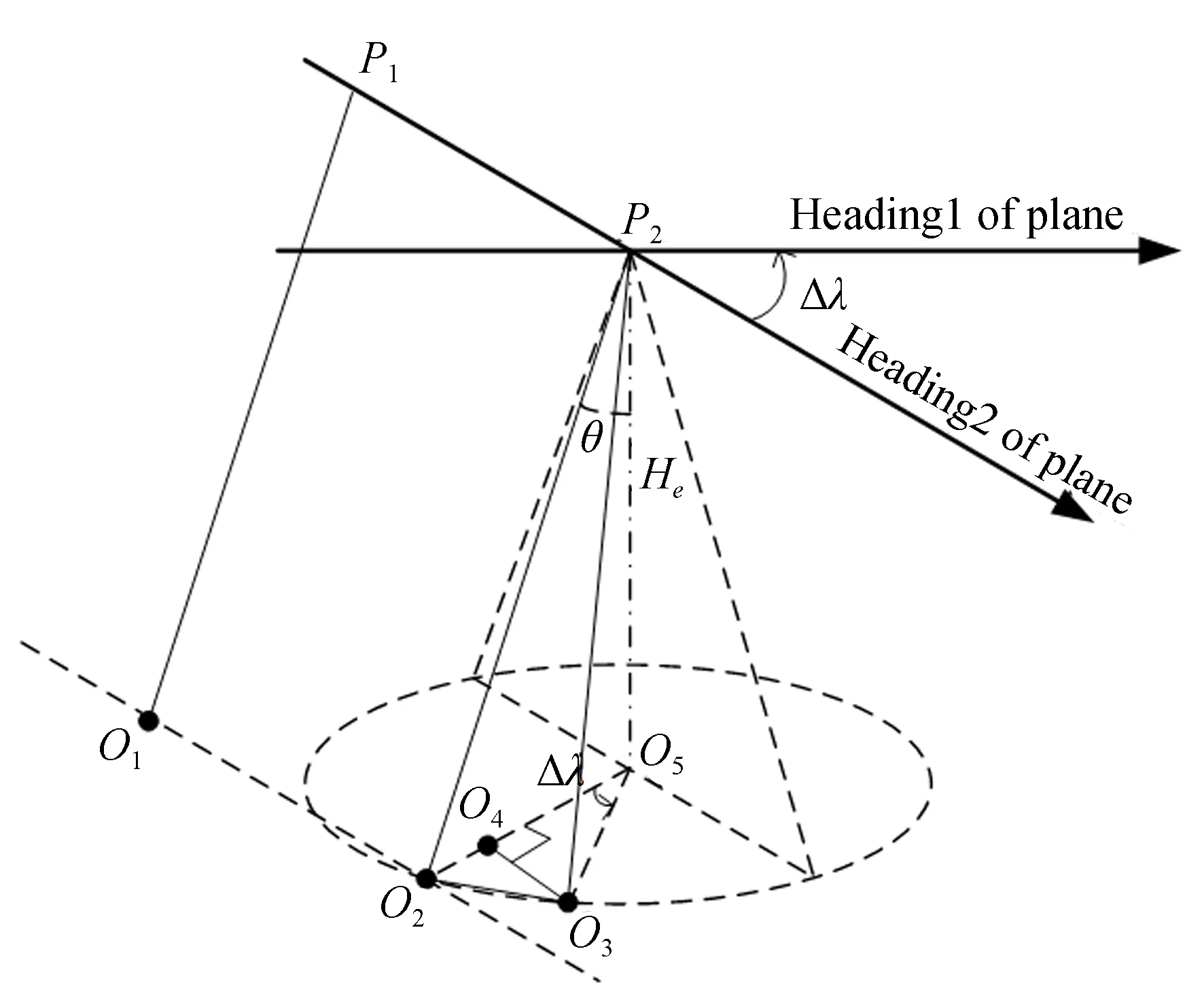
图4 航向角变化对重叠率影响Fig.4 Effect of heading variation for overlap

下面分析θ=74°，ω=0.88°，飞机航向角变化Δλ为0°～1°时对重叠率影响，表1给出了飞机航向角变化对重叠率影响分析结果。分析结果表明，当航向角变化0.2°时重叠率变化量为21.85%，影响显著需要对航向角的变化进行补偿。

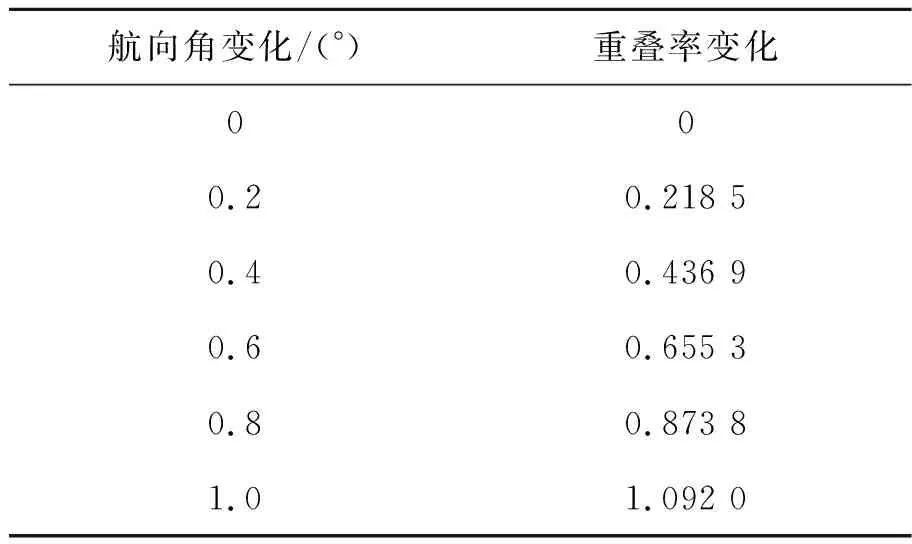
表1 航向角变化对重叠率影响

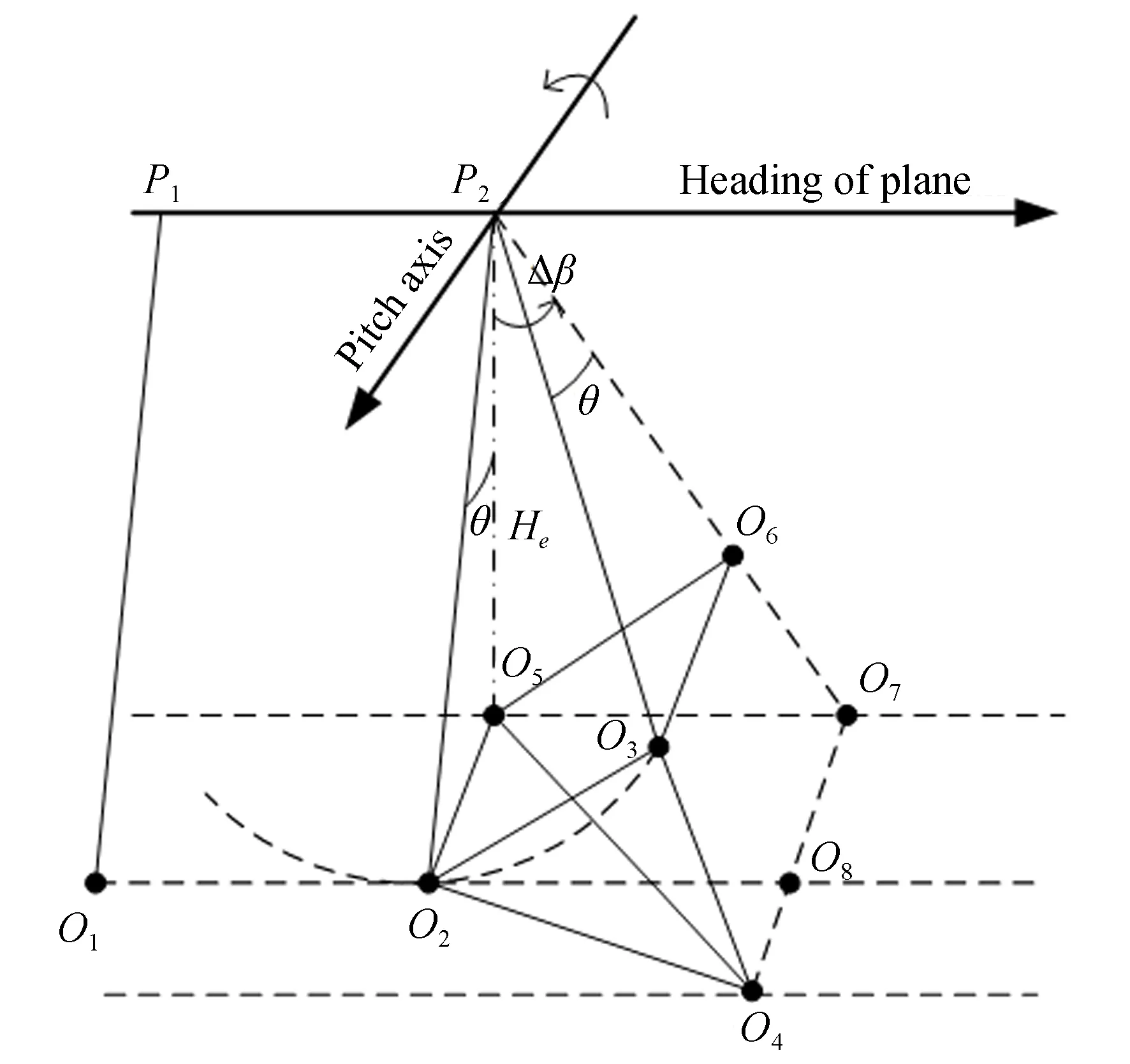
图5 俯仰角变化对重叠率影响Fig.5 Effect of pitch variation for overlap

其次分析仅存在飞机俯仰角变化对重叠率的影响。图5中前一条带飞机位于位置P1，对应地面近地端为位置O1；当不存在飞机俯仰变化时，后一条带图像飞机位于位置P2，对应地面近地端为位置O2。如果相对位置P1，在P2位置飞机俯仰角存在Δβ的波动时，相机视轴位于与俯仰轴夹角为90°-θ的圆锥面上运动，线段O2O5运动到O3O6，P2O3与地面的交点为O4，P2O6与地面相交于点O7，连接O4O7。在飞机俯仰角变化过程中，O3O6始终平行于地平面，因此O3O6平行于O4O7，O2O5，可推导出O4O7平行于O2O5，直线O5O7为飞机航迹P1P2在地面投影且O5O7与O1O2平行，O2O5与O5O7垂直，有O4O7垂直于飞机飞行航线在地面投影O1O2，垂足为O8。因此，O2O8长度即为飞机俯仰变化产生的图像实际成像点与目标点偏差，LO2O8=LO5O7=Hetan Δβ

对重叠率的影响为:

(19)

下面分析θ=74°，ω=0.88°，飞机俯仰角变化Δβ为0°～1°时对重叠率影响，表2给出了飞机俯仰角变化对重叠率影响分析结果。分析结果表明，当俯仰角变化0.6°时重叠率变化量为19.2%，影响显著需要对航向角的变化进行补偿。

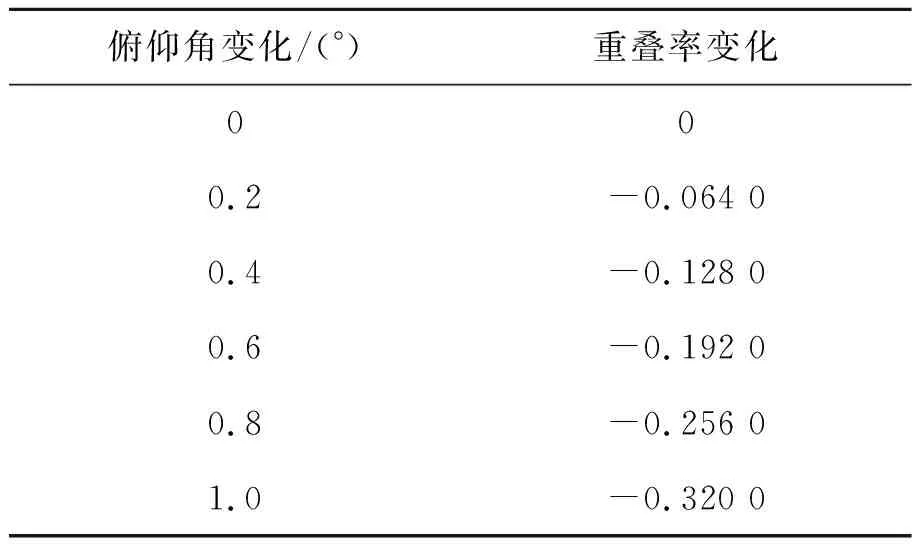
表2 俯仰角变化对重叠率影响

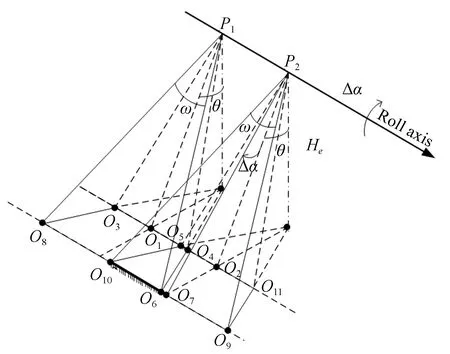
图6 横滚角变化对重叠率影响Fig.6 Effect of roll variation on overlap

再分析仅存在飞机横滚波动对重叠率的影响。图6中前一条带飞机位于位置P1，对应地面近地端为位置O1，当不存在飞机横滚变化时，后一条带图像飞机位于位置P2，对应地面近地端为位置O2，对应图像重叠区域为O4O5。如果飞机在P2位置存在横滚角Δα的波动时，对应地面近地端为位置O7，近地端重叠区变为O6O10。横滚角变化改变飞行方向单帧覆盖长度进而对重叠率产生影响。

在视轴指向角为θ时，重叠率表达式为:

(20)

在相邻条带飞机飞行距离和高度保持不变的情况下，重叠率随着视轴指向角θ的增大而变大。

飞机横滚角变化引起重叠率变化为:

(21)

其中ρ0为预期的重叠率。因此，

(22)

下面分析θ=74°，ω=0.88°，飞机横滚角变化Δα为0°～1°时对重叠率影响，表3给出了飞机横滚角变化对重叠率影响分析结果。分析结果表明，当横滚角变化0.6°时重叠率变化量为3.11%，也需对航向角的变化进行补偿。

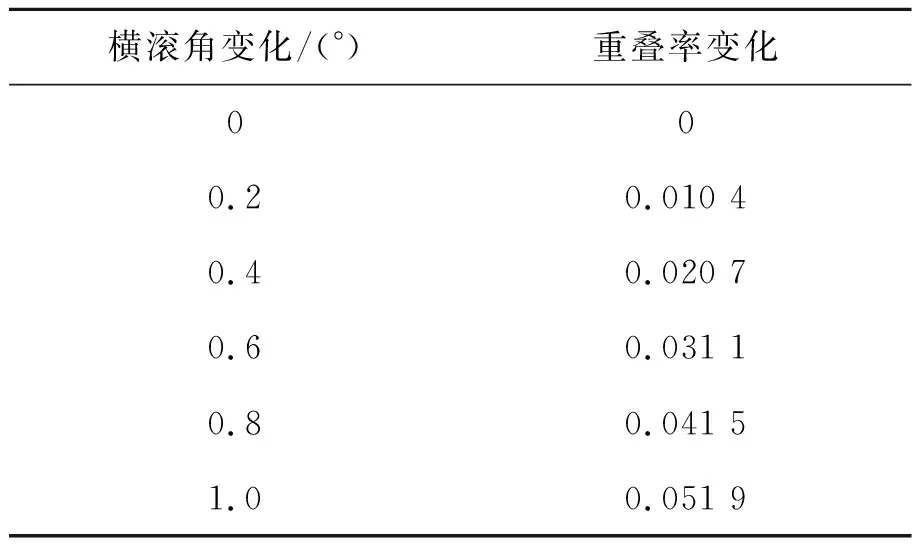
表3 横滚角变化对重叠率影响

在实际成像中飞机的三个姿态角将同时存在，此时很难通过几何方法进行重叠率分析，通过坐标变换方法计算仿真飞机姿态角对重叠率的影响更适合。设T0时刻飞机俯仰角和横滚角均为0°、航向角为180°，相机的位角为0°、俯角为74°、右倾斜成像；在T1时刻，飞机航向、俯仰、横滚角分别为179°，1°，1°，相机的位角、俯角维持不变。图7中点划线为T0时刻成像区域，实线为预期的T1时刻图像区域，角落带点的虚线框为存在飞机姿态角影响的图像区域。可以看出存在飞机姿态角影响时图像成像区域与预期区域相距甚远，图像将存在拉缝，需要对飞机姿态角影响进行补偿。

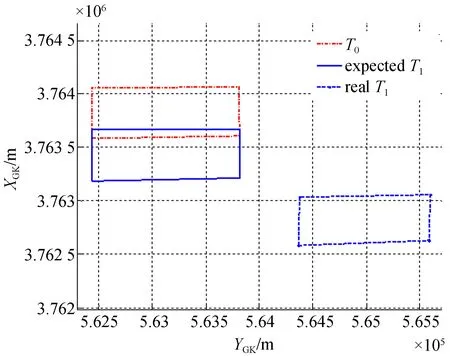
图7 载机姿态角综合影响Fig.7 Synthetic effect of plane attitude

可以通过调整相机的位角和俯角角度抑制飞机姿态角影响，并通过坐标变换的方法计算相机位角和俯角的补偿量。

视轴在相机坐标系下的坐标为LOSS=[0,0,1]T，在NED坐标系下的坐标为:

(23)

设前一条带近地端成像T0时刻飞机的航向角、俯仰角及横滚角分别为λ0,α0,β0，相机的位角为φ0、俯角为θ0，后一条带近地端成像T1时刻飞机航向角、俯仰角及横滚角变化量分别为Δλ,Δα,Δβ。

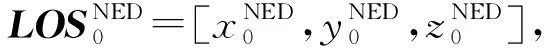
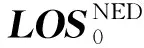
(24)

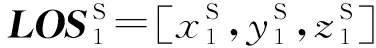
相机位角的修正量Δφ和俯角修正量Δθ分别为式(25)、式(26):

(25)

(26)

针对图7的仿真条件，利用式(25)和式(26)计算的位角修正量为Δφ=0.618°、位角修正量为Δθ=-1.016°，图8给出补偿后的结果。可以看出，通过相机位角和俯角补偿后，成像区域几乎与预期一致，仅存在一些投影产生的图像畸变。

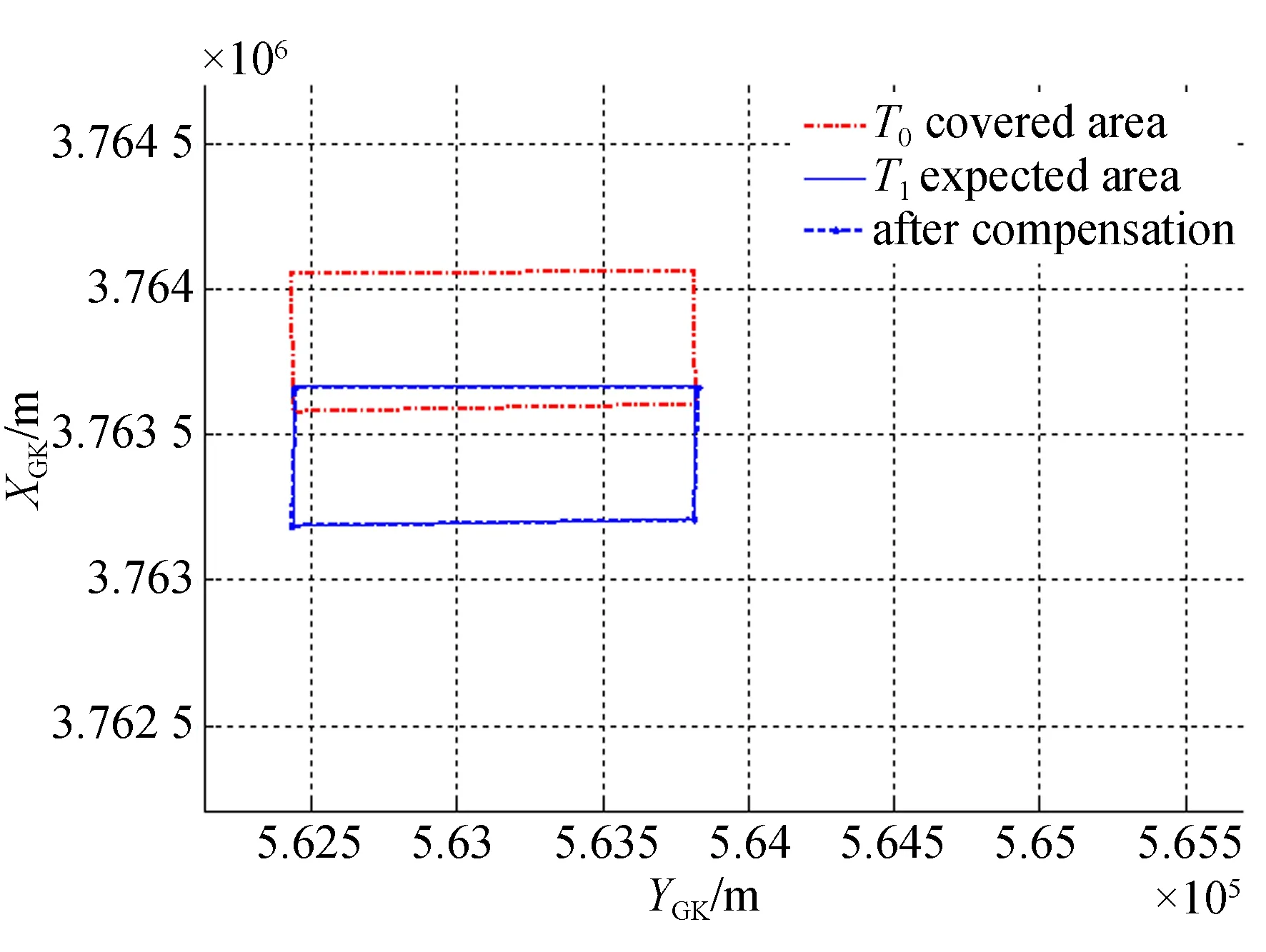
图8 飞机姿态角影响补偿结果Fig.8 Result of compensation for plane attitude

3.2 载机高度变化影响及补偿

对于定焦相机其视场角ω是固定的，沿飞行方向单帧覆盖的长度与成像距离成正比。如果T1时刻后一条带图像对应飞机高度HP2与T0时刻前一条带飞机高度HP1相比存在变化，也会对重叠率产生一定的影响。对于重叠率而言，载机高度的变化可等效为地面高度的变化，两者符号相反，即:

ΔHe=ΔHP=HP2-HP1=hT1-hT2=-ΔhT.

(27)

(28)

当T1时刻后一条带飞机高度与T0时刻比增加时，重叠率相应增加。当T1时刻后一条带成像目标区高度与T0时刻比减小时，重叠率相应减小。

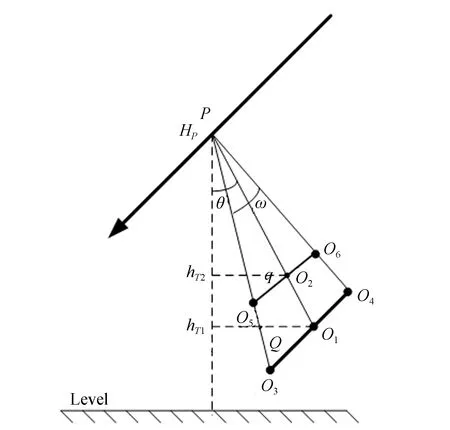
图9 高度对覆盖长度影响Fig.9 Effect of target height variation on cover length

可以通过实时采集判断载机当前位置(含载机高度)、载机速度、视轴指向等信息实时估算出保证图像重叠率下一条带开始时机，据此对相机的拍照周期进行调整，可有效抑制载机或目标高度变化对重叠率的影响。

3.3 飞机飞行速度影响及补偿

相邻条带图像近地点中心距离与飞机飞行的距离是相同的，在飞机飞行高度、速度维持不变的情况下，固定拍照周期即可实现预期的重叠率。相邻条带的拍照周期为:

(29)

其中:ω为飞行方向视场角，ρ为预期重叠率，V为飞机对地速度，He为飞机对地高度，θ为扫描成像条带开始位置视轴与水平方向的夹角。此时重叠率为:

(30)

相邻条带载机的飞行平均速度变化为ΔV时，重叠率变化为:

(31)

维持ΔVT不变，则可消除载机速度波动带来的影响。存在载机速度波动时，相邻条带载机飞行距离为:

(32)

公式(30)变为:

(33)

为实现预期重叠率，相邻条带载机飞行距离满足如下关系:

(34)

通过调整拍照周期T来调整相邻条带载机飞行距离，进而解除拍照过程中对飞机速度恒定的限制。

同时考虑载机相对目标高度He和载机速度V实时变化时，公式(33)可描述为:

(35)

其中ξ为载机相对目标实时速高比，由公式(35)可得:

(36)

因此，依据预期重叠率计算实时速高比积分，求解相邻条带拍照周期T消除载机速度和相对目标高度的影响，拍照过程中无需限制相机恒速、恒高飞行。

4 重叠率实际飞行结果

对某型航空相机实际飞行数据进行分析。图10中O标识实线为相邻条带飞机航向角变化角度，△标识实线为飞机横滚角的变化情况，□标识实线为飞机俯仰角变化量。

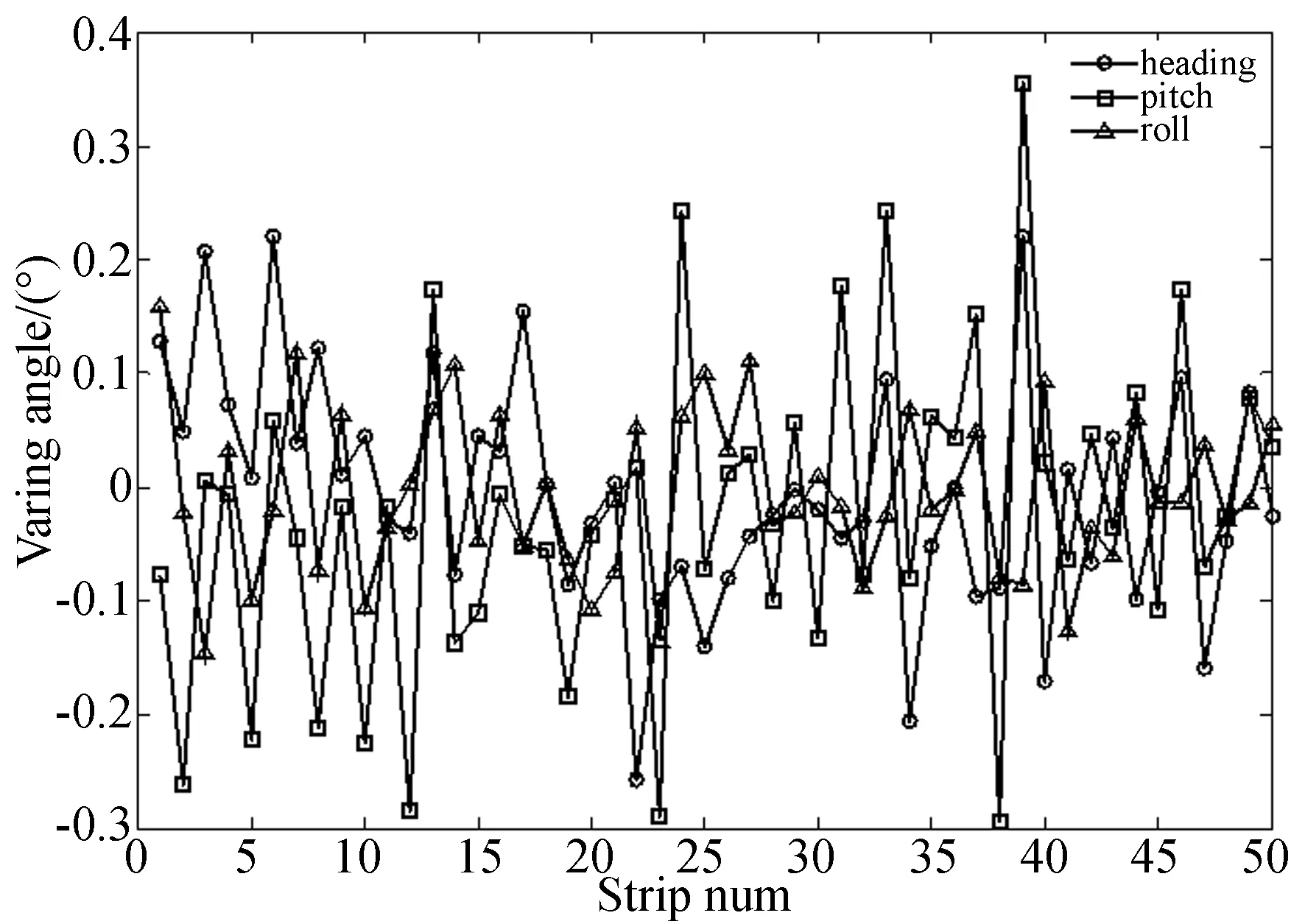
图10 飞机姿态角波动Fig.10 Variation of plane attitude

图11 平坦地区航拍图像Fig.11 Flight images of flat area

图11为平坦地区实际飞行图像的重叠率情况。表4为图11重叠率结果对应的载机实际飞行参数、相机角度。从实际结果看出，在平坦地区获取图像重叠率均值为16%与预期值15%相差1%。

图12给出对地表高度起伏比较大的山区进行成像时重叠率均值为7%，明显低于预期的15%。通过查阅Google地图并对比相机成像区域分析，预期目标被海拔高度为1 000 m左右的高山遮挡，因此实际成像景物海拔高度为1 000 m，整个飞行任务设置的地面目标高度为380 m，飞机海拔高度为8 460 m，实际成像目标的海拔高度大于设置的目标海拔高度对重叠率的影响与飞机高度降低是一样的，依据公式(28)可知，相当于ΔHP=-620 m，He0=8 080 m，实际重叠率与预期值偏差为Δρ=-7.7%，重叠率为7.3%，与实际飞行结果相符。由于目标区高度和载机高度变化对重叠率影响的机理相同，在依据载机高度变换进行拍照周期调整中引入目标区的DEM数据[14]，实时估算目标区高度并调整相机的工作参数，将有效降低地表高度变化对重叠率影响。

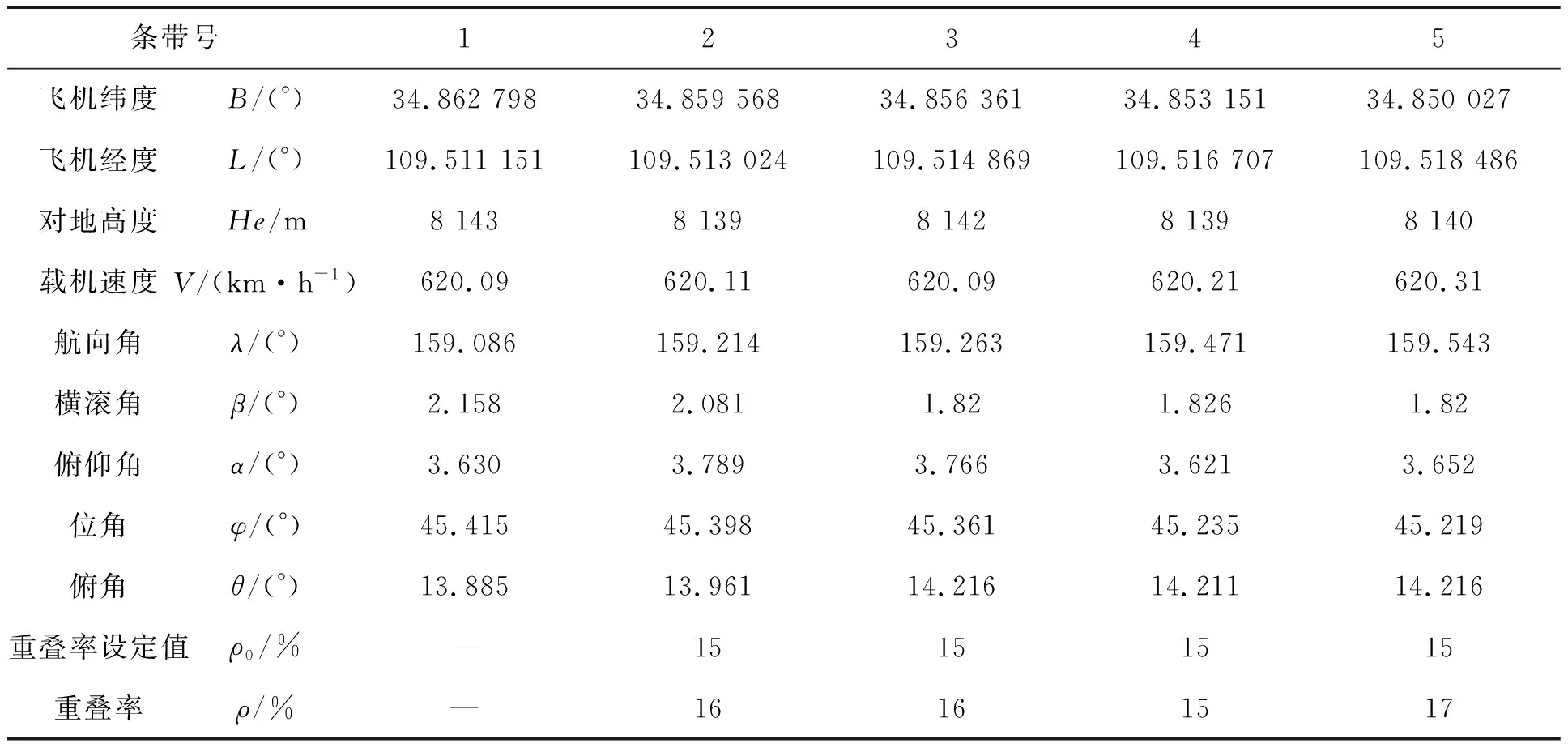
表4 实际飞行重叠率结果

图12 山区航拍图像Fig.12 Flight images of mountain area

5 结 论

针对航拍相邻条带图像间载机的航向角、俯仰角、横滚角、载机飞行高度、飞行速度等5个飞行参数变化对重叠率的影响进行了研究，给出了基于坐标变换的大倾斜成像重叠率分析方法。对于载机姿态角单变量影响情况，通过几何分析方法进行了重叠率影响的定量分析；对于载机姿态角综合作用影响，利用基于坐标变换的方法给出了在波动在1°范围内的分析结果，提出使用相机位角和俯角对载机姿态角的影响进行补偿，利用坐标变换的方法给出了相机位角和相机俯角补偿量的计算公式。对于载机速度和载机高度波动给出了基于几何分析方法的重叠率影响定量分析，提出了调整拍照周期进行补偿的方法，并给出了相应计算方法。实际飞行结果表明，在平坦地区，重叠率均值与预期值间相差1%。在山区，受地表起伏的影响，未进行地表目标高度修正，重叠率小于预期值，偏差为8%。

提出的基于坐标变换的分析方法可以很好的用于指导大倾斜成像航空相机的重叠率设计及指导实际飞行图像的重叠率分析与修正。另外，相机的位角和俯角控制偏差、目标区地表起伏变化对重叠率也有一定影响，在后续工作中进行研究。