大倾角远距离航空成像的修正系统误差定位方法

李 彬，丁亚林，修吉宏，李 军，乔 川

(1. 中国科学院 长春光学精密机械与物理研究所 中国科学院航空光学成像与测量重点实验室，吉林 长春 130033；2. 北京控制工程研究所，北京 100190)

1 引 言

为了快速获取地面目标信息，目前的航空相机在进行高分辨率成像外，还要同时获得地面目标的定位信息[1-2]。为了实现地面目标定位功能，国内外学者针对航空相机对地目标定位算法进行了大量研究。周前飞等[3]利用像元视线向量法，建立了机载光电平台多目标自主定位系统，实现了对多目标的实时定位。张赫等[4]针对小型机载光电平台利用扩展卡尔曼滤波方法，基于椭球模型进行目标定位。这些算法针对成像距离为15 km以内的目标进行定位，采用激光测距装置获得目标距离信息，不适用于远距离航空成像。

Hosseinpoor等[5-6]利用搭载了全球定位系统(Global Positioning System，GPS)的无人机对目标区域进行反复成像，采用扩展卡尔曼滤波对数据进行处理，实现目标定位。孙辉等[7]提出对目标多次成像，采用最小二乘法计算目标的定位信息。徐诚等[8]采用无迹卡尔曼滤波方法对多次成像的目标进行定位计算。这些方法都需要对静止目标进行多次成像，不适用于大倾角一次成像的功能要求。

杨洪涛等[9]提出基于地球平面模型计算目标定位信息，由于没有考虑地球曲率，所以不适用于远距离成像。Helgesen等[10]和Stich等[11]提出基于WGS-84坐标系定义的椭球模型进行目标定位计算，考虑了地球曲率，但不适用于地形起伏很大的目标区域。杜言鲁等[12]依据已知的视轴指向角，利用地球椭球模型计算目标位置信息，并分析了目标大地高对定位精度的影像。乔川等[13]提出了依据地球椭球模型进行目标定位计算，给出了坐标转换矩阵，并代入了目标区域的数字高程模型(Digital Elevation Model, DEM)，但在大倾角远距离航空成像实际应用时，会产生较大的定位误差。

本文针对在大倾角远距离航空成像时对地目标算法的误差进行分析，提出了一种可以修正系统误差的大倾角远距离航成像修正系统误差定位方法。该算法在基于椭球模型和中心投影原理的对地目标定位算法的基础上，加入了系统误差修正模型，修正了探测器安装误差、组合惯导安装误差以及相机转轴安装误差。误差修正参数包括地面标定获得的标定误差参数以及残余误差参数，针对不能进行实验室标定的残余误差参数给出了一种地面控制点计算残余误差方法，并通过仿真实验证明了该方法的有效性。最后，利飞行试验数据验证，在大倾角远距离航空成像应用时，本方法可以修正目标定位中的系统误差，提高定位准确性。

2 算法原理

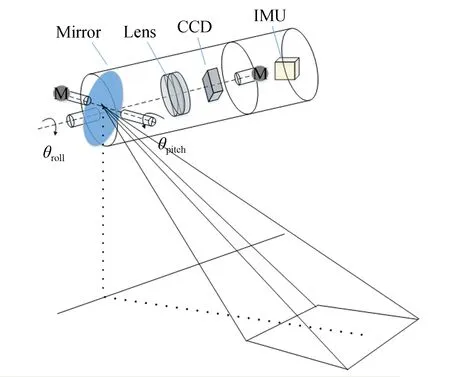
图1 远距离航空相机结构示意图Fig.1 Schematic diagram of long-distance aerial camera

目标定位指的是能有效获取航拍影像中目标区域的地理位置信息，对拍摄区域进行进一步分析和处理。目前机载相机逐步安装有POS系统用于定位功能。POS系统由GPS和惯性测量单元(Inertial Measuring Unit, IMU)组成，可以准确测量载机位置信息和姿态信息，在导航、摄影测量等领域得到了广泛应用[14]。

大倾角远距离航空相机结构如图1所示。相机安装在飞机底部，沿飞机飞行方向布置。相机俯角镜筒转轴与载机横滚轴一致。当俯角镜筒在初始位置时，位角摆镜转轴与载机俯仰轴平行。在拍摄过程中，通过转动镜筒和摆镜，可以控制相机的视轴指向，进行连续摆扫成像。POS系统与飞机惯导共用一个GPS天线，天线安装在飞机顶端。IMU单元安装在相机后罩内，不随俯角镜筒转动。

当相机对地面拍照时，地面点光线通过扫描反射镜及物镜组成像在探测器上，符合中心投影原理[15]，其简图如图2所示。

对于理想光学系统，投影中心、物点、像点三点共线。以相机投影中心S为原点，建立相机坐标系S-XSYSZS，SZS是视轴指向。过像面上目标投影点T′与相机坐标系原点S建立一条直线，则真实目标点T在这条直线上。

图2 航空相机对目标成像示意图Fig.2 Imaging of target by aerial camera

根据WGS-84坐标系定义，建立基于地球椭圆模型的地球坐标系(ECEF)E-XEYEZE。原点E为地球质心，EXE轴指向本初子午线与赤道交点，EZE指向北极，与EYE组成右手坐标系。

(1)

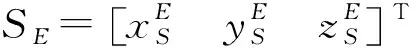
由于目标点在地球水平面以上，应满足椭球方程[16]，即有：

(2)

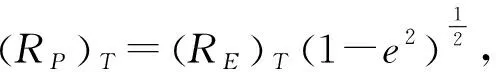
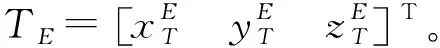
(3)

依据式(3)得到目标所在椭球半径初值(RNT)0，目标大地高初值(hT)0及目标纬度初值(φT)0。然后建立迭代方程组：

(4)

依据式(4)迭代4次求解得到目标点T的纬度φT和目标大地高hT。根据经度定义有方程：

(5)

解方程(5)得到目标点经度λT。

3 系统误差修正

根据地目标定位算法原理可以知道，计算定位信息需要通过坐标转换得到目标投影点T′和相机投影中心S在地球坐标系(ECEF)下的坐标。因为坐标转换过程包含一些误差项，随着对地目标距离的增大，误差影响也会增大。所以在进行大倾角远距离航空成像时，对地目标定位算法的定位结果会有很大偏差，无法满足工程需要。

定位结果偏差的主要因素包括测量误差和系统误差。测量误差包括组合惯导在拍摄过程中给出的地理信息测量误差和姿态信息测量误差，以及俯角镜筒和位角摆镜转轴上的轴角传感器在拍摄过程中给出的角信息测量误差。这些测量误差是服从正态分布的随机误差。系统误差包括探测器安装误差、组合惯导安装误差以及位俯角转轴安装误差。对于某一台航空相机，在装调状态稳定后，其系统误差也会相对保持稳定，所以可以通过实验标定和优化计算模型来消除。

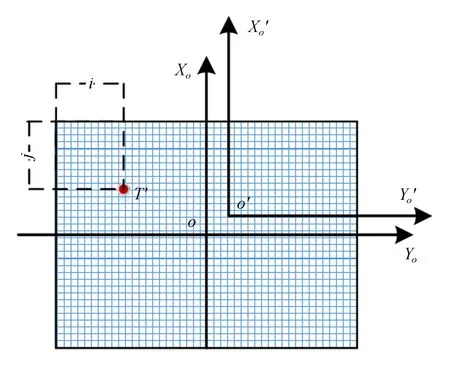
图3 目标在像面上的投影点Fig.3 Projection point of target on detector

3.1 探测器安装误差修正

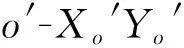
若探测器像元尺寸为α，像元数为M×N,目标投影T′在像面内坐标为(i,j)，相机经过主点偏差标定实验得到主点o′在相面坐标系坐标(xo′,yo′)。如图3所示，可得加入探测器安装误差修正模型后，目标在探测器上投影点T′在相机坐标系S下的坐标为：

(6)

3.2 组合惯导安装误差修正

组合惯导由GPS和IMU组成。GPS安装在飞机顶端，可以给出相机在拍照过程中的地理信息；IMU安装在相机后罩内，在拍照过程中给出相机姿态信息，如图4所示。组合惯导的安装误差一方面会导致IMU给出的相机姿态与实际姿态不一致，另一方面如果不考虑GPS安装位置，则GPS给出的高度信息与相机实际高度会存在不一致。

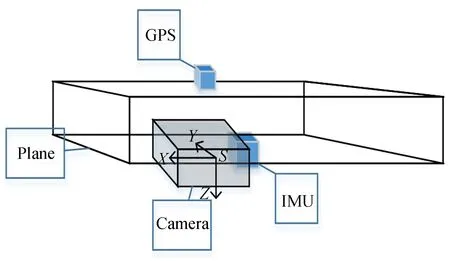
图4 POS安装示意图Fig.4 Assembly of POS

建立地理坐标系(NED)S-NED，原点与相机坐标系原点S重合，地理坐标系SN和SE坐标轴分别指向正北和正东，SD轴指向地心，垂直于当地参考椭球的切线。GPS给出的位置信息包括相机经度λS、相机纬度φS和相机大地高hS。测量得到安装后GPS中心点与相机坐标系高度差为h′。依据几何关系建立方程组：

(7)

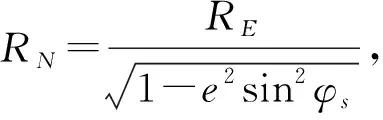
(8)

建立相机机身坐标系[17](AC)S-XYZ，原点与相机坐标系原点S重合。当相机处于初始状态，即俯角镜筒和位角摆镜都处于零位时，相机机身坐标系和相机坐标系重合。IMU与相机机身刚性连接，在相机工作过程中，IMU需要给出相机机身姿态信息，包括航向角y、俯仰角p和横滚角r。理想状态下，IMU坐标系与相机坐标系可以通过平移后重合，但实际存在安装误差，使两个坐标系存在旋转角。所以需要在IMU安装后，经过地面标定，给出航向、俯仰和横滚3个方向的安装误差角Φy，Φp，Φr。标定后仍然残留的安装误差角用δy，δp，δr分别表示。加入IMU安装误差修正模型后，从相机机身坐标系(AC)到地理坐标系(NED)的变换矩阵为：

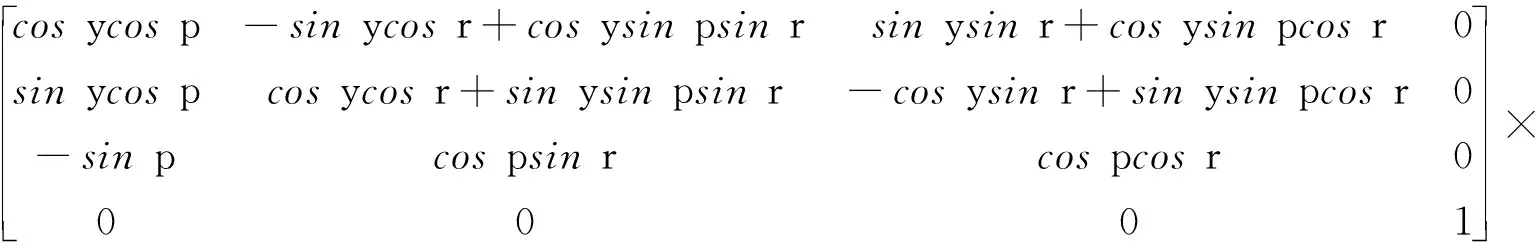
(9)

3.3 相机转轴安装误差修正

相机在转轴装调的理想状态是保证俯角镜筒转轴与相机坐标系XS轴平行，在俯角镜筒处于零位时，位角摆镜转轴与相机坐标系YS平行。但在实际操作中，装调结束后仍会存在转轴安装误差，导致两个旋转轴与相机的横滚俯仰方向不一致。在相机拍照过程中，安装在转轴上的轴角传感器会输出转轴的角度，轴角传感器输出值需要根据相机结构和光学设计转换到相机坐标系中，用α表示绕XAC旋转角，β表示绕YAC旋转角，用δα和δβ分别表示俯角镜筒转轴和位角摆镜转轴的安装误差角。加入转轴安装误差修正模型后，从相机坐标系(S)到相机机身坐标系(AC)的变换矩阵为：

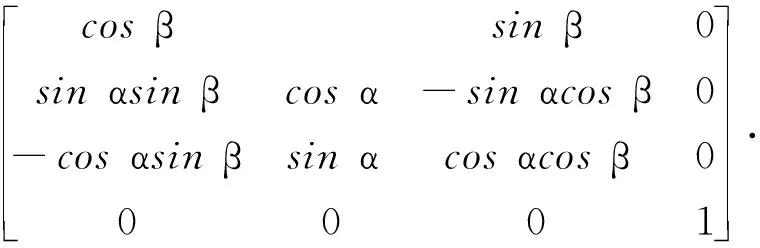
(10)

3.4 利用地面控制点估计残留误差参数

通过系统误差修正模型可以看出，除了可以在地面标定实验中得到的标定误差参数外，还需要知道残留误差参数。当一台相机装调稳定后，系统误差会保持相对稳定，所以可以利用航拍得到图像中的地面控制点来计算得到残留系统误差参数。

已知地面控制点T的地理信息为纬度φT，经度λT，大地高hT，可以建立方程：

(11)

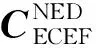
对控制点T成像，可以得到控制点在探测器上的像，即控制点投影点T′在像面内坐标(i,j)。依据公式(6)可以得到控制点投影在相机坐标中的坐标T′S。根据中心投影原理可知，控制点T与像点T′的连线经过投影中心，同时分属与原点两侧，则可建立方程：

(12)

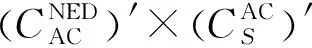
(13)

为方便表述，记:

(14)

(15)

在计算过程中可忽略二阶小量，依据式(12)整理为：

(16)

令：

(17)

(18)

整理式(16)得到：

(19)

采用最小二乘法对5个系统误差未知量进行估计。当获得n个控制点的成像后，每个控制点成像可得到3个方程，X成为3n×5的矩阵，y成为3n×1的矩阵。利用最小二乘法得到：

(20)

4 仿真实验

利用Matlab对估计残留系统误差参数过程进行仿真实验。假定组合惯导的安装误差为航向方向0.030°，俯仰方向-0.015°，横滚方向0.012°，相机转轴的安装误差为俯角镜筒转轴误差角0.010°，位角摆镜误差角-0.020°。控制点T的地理信息为33.980 849°N，107.523 239°E，3 132.10 m，相机在不同的位置对控制点进行5 000次成像测量。计算得到残留系统误差参数如图5所示。

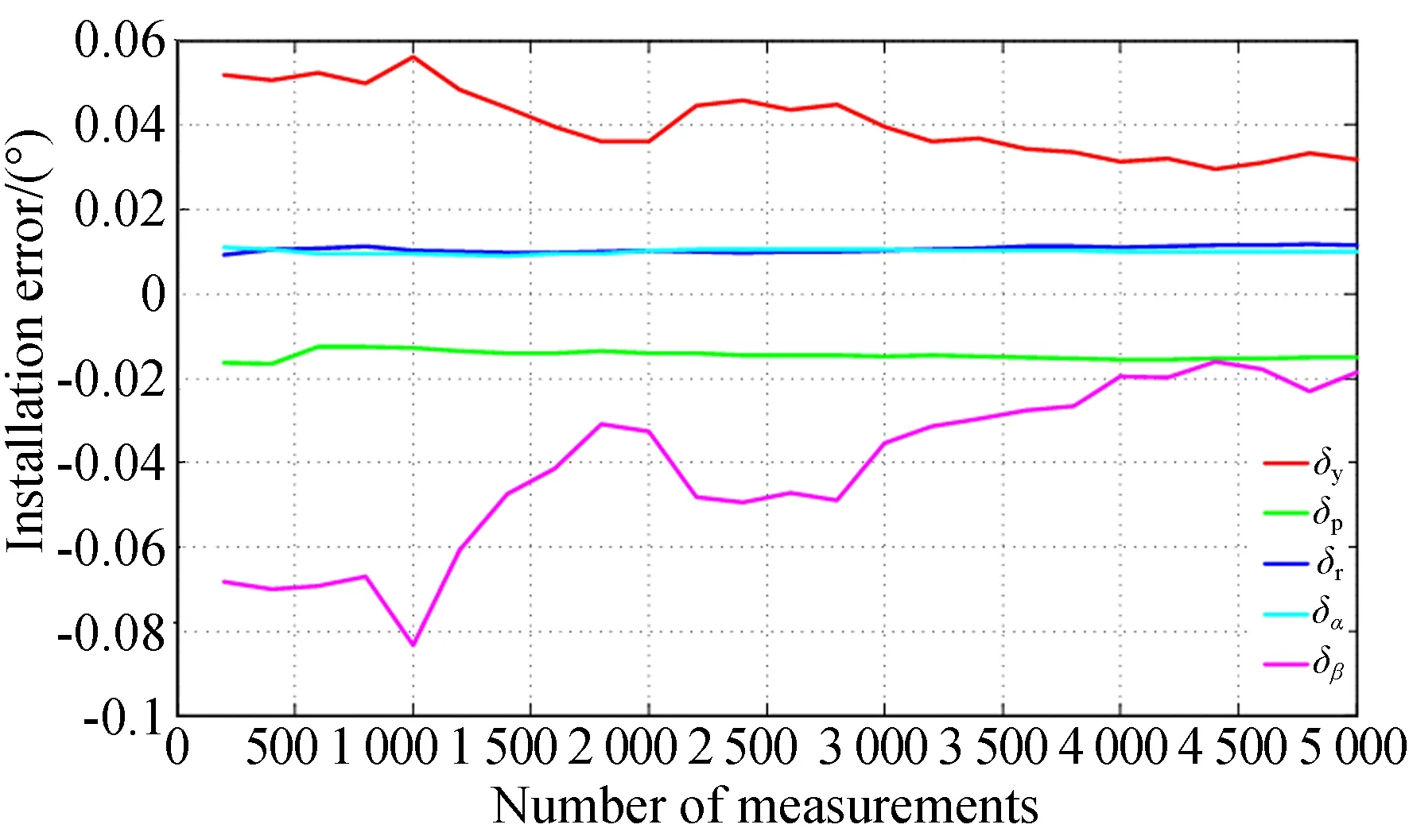
图5 残留误差计算结果Fig.5 Computation results of residual errors

由图5可以看出，经过对控制点4 000次成像测量后，计算得到这5个安装误差分别为：组合惯导残留安装误差为航向方向0.031 2°，俯仰方向-0.015 6°，横滚方向0.011 1°；相机转轴的残留安装误差为俯角镜筒转轴误差角0.010 0°，位角摆镜误差角-0.019 6°。与设定的安装误差相比，计算误差为0.0013°，-0.0003°，0.001 0°，0.000 0°，-0.000 3°，仅为原来残留安装误差的1/10。实验结果表明，利用地面控制点估计残留系统误差参数的方法可以有效估计出残留系统误差。

5 飞行试验

以某远距离大倾角航空相机航拍图像为实验数据，成像距离大于25 km，倾角大于70°。依据拍摄图像注释信息可获得组合惯导得出的拍照时刻的位置信息和姿态信息，相机转轴轴角传感器给出的俯角镜筒角和位角摆镜角，以及目标区域的DEM信息。经过计算得到目标定位结果，如图6所示。

图6(a)为没有进行系统误差修正的对地目标定位算法结果，定位误差最大值为545 m，最小值为310 m，定位圆概率误差为397.7 m，定位平均误差为401.25 m。图6(b)为修正了探测器安装误差的定位结果，定位误差最大值为345 m，最小值为140 m，定位圆概率误差为224.8 m，定位平均误差为230.8 m。图6(c)为修正了组合惯导安装误差的定位结果，定位误差最大值为290 m，最小值为70 m，定位圆概率误差为152.9 m，定位平均误差为160.0 m。图6(d)为修正了所有系统误差的定位结果，定位误差最大值为200 m，最小值为23 m，定位圆概率误差为99.2 m，定位平均误差为97.5 m。对比发现，修正系统误差定位方法可以提高大倾角远距离成像定位结果，定位误差从平均值401.25 m降到97.5 m，满足实际工程要求。

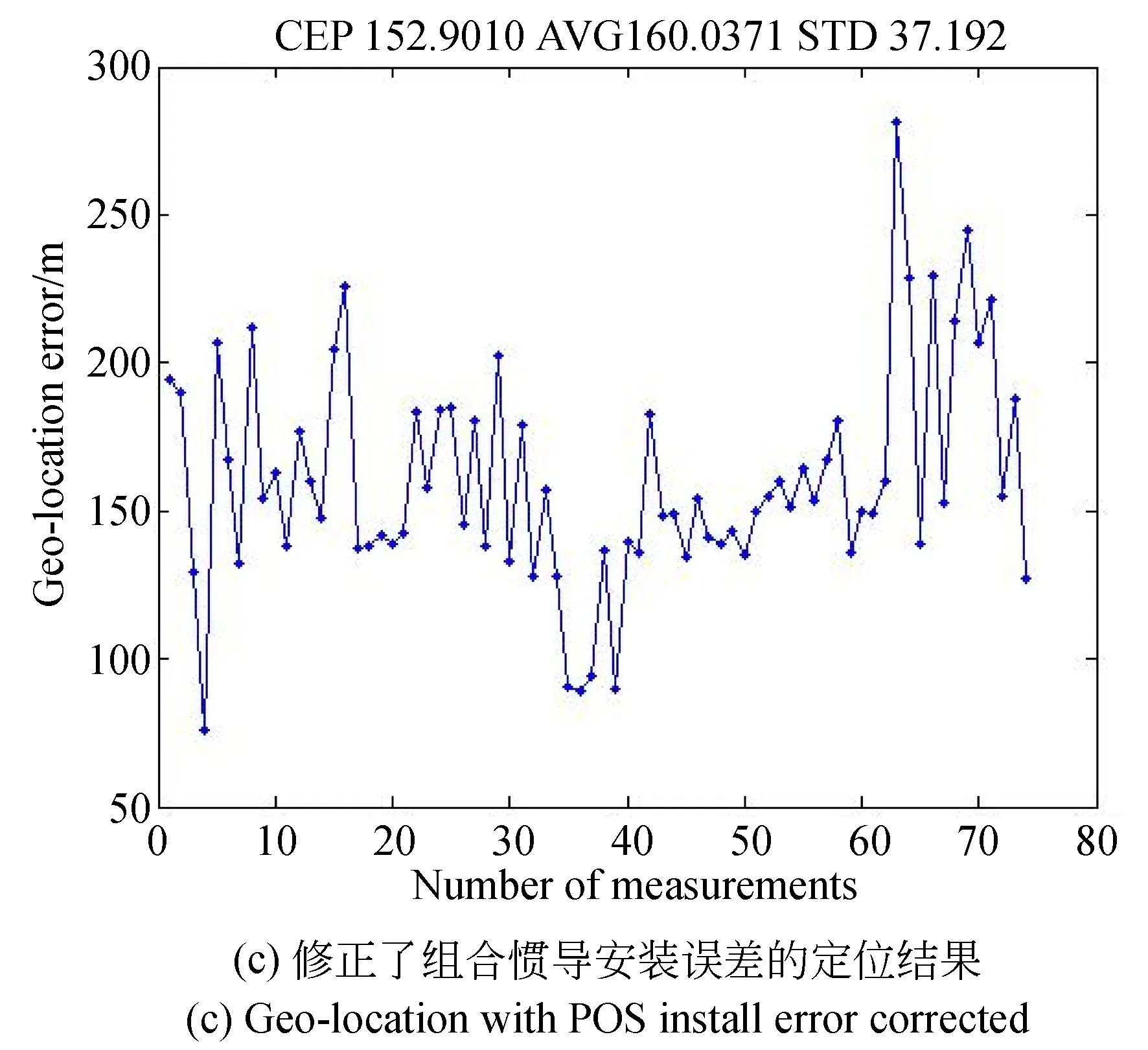
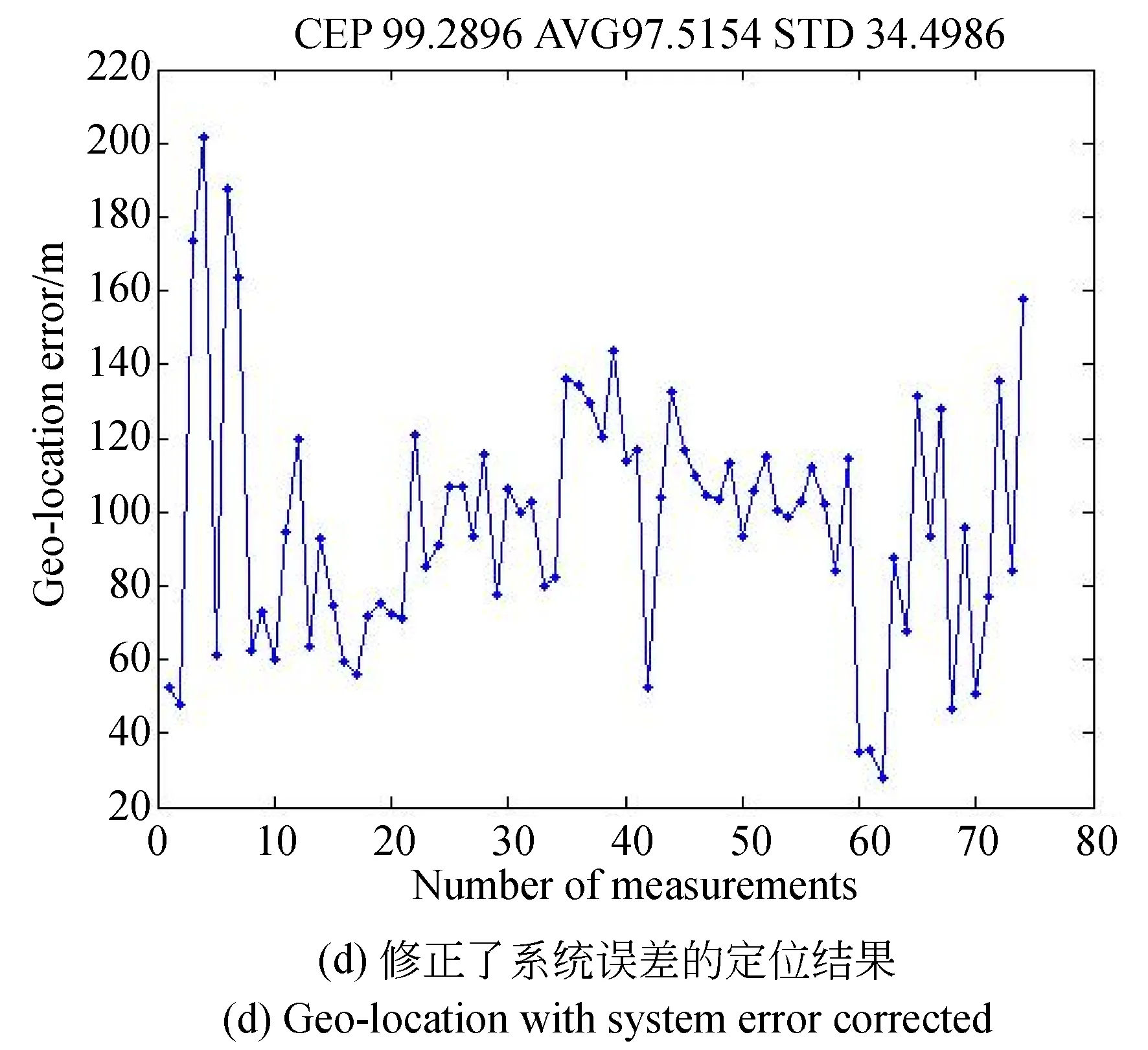
图6 飞行试验定位结果

6 结 论

本文通过分析大倾角远距离航空成像系统的系统误差，提出了探测器安装误差修正模型、组合惯导安装误差修正模型、相机转轴安装误差修正模型，并在此基础上提出了修正系统误差定位方法。对无法在地面标定获得的残留系统误差参数，给出了一种依据地面控制点利用最小二乘法估计误差参数的方法。仿真实验标明，估计参数可将残余误差降至1/10。最后进行了飞行试验，结果表明，定位误差平均值从401 m降低到97 m，该方法能有效降低对地目标定位误差。