交换折叠超立方体的超连通度

蔡学鹏, 马 丽

(新疆农业大学 数理学院,新疆 乌鲁木齐 830052)

引言

众所周知,互连网络在并行计算及通信系统中发挥着重要作用。一个网络的拓扑结构在数学上通常被抽象的模型化为一个图G=(V(G),E(G)),其中V(G)是图G的顶点集来表示网络处理器的集合,E(G)是图G的边集来表示网络的通信链路集。在本文中,术语图和网络可以互换使用。本文中所有的图都认为是无向的,简单的和连通的,对于未说明的图论符号和术语,可参考文献[1-2]。

设G=G(V,E)是一个图，对于图G中两个子图H和K，记G-H是点集V(G)-V(H)诱导的子图。设NH(K)是在H中且与K中的点相邻的点的集合，特殊地，如果K={v}，可记作NH(v)。设dG(v)=|NG(v)|是点v在图G中的度，设NG[v]=NG(v)∪{v}。如果不产生歧义，我们可省略下标即记为d(v),N(v),N[v]。δ(G)=min {d(v)|v∈V(G)}表示图G的最小度。图G的最小边度定义为ξ(G)=min{d(u)+d(v)-2|(u,v)∈E(G)}。

图G的经典连通度κ(G)和边连通度λ(G)是衡量网络可靠性和容错性的两个重要参数[3-4]。连通度κ(G)和边连通度λ(G)越大,网络的可靠性就越高。但是,这两个参数有明显的不足之处,比如,在互连网络的实际应用当中,与一个处理器相连接的所有处理器(链路)同时发生故障可能性较低,所以这两个参数衡量网络可靠性和容错性是不精确的。为克服这些不足之处,Esfahanian在文献[5]中提出了超连通度(超边连通度)的概念,超连通度(超边连通度)比连通度(边连通度)能更好地衡量网络可靠性和容错性。

设S⊆V(G)(S⊆E(G))，如果图G-S不是连通的,并且毎个分支都至少包含两个顶点,则称S是G的一个超点割(超边割)。若图G存在超点割(超边割),则G的所有超点割(超边割)中基数最小的超点割(超边割)的基数称为G的超连通度(超边连通度),记为κ(1)(G)(λ(1)(G))。超连通度(超边连通度)已经在许多互连网络(图)中得到了研究,见参考文献[6-12]。

在平行计算系统中，n维超立方体Qn[13-14],n维折叠超立方体FQn[15]和交叉超立方体EH(s,t)[16]是三个重要的互连网络。基于这三个网络，李等人在2005年[17]提出了一个新的网络交换折叠超立方体EFH(s,t)。EFH(s,t)是在EH(s,t)的基础上增加了一些额外的边获得的并且这些边称为补边，交换折叠超立方体有许多重要的特性，比如它有短的直径和低消费因子。最近Bhavani[18]等人研究了交换折叠超立方体的短路径问题。

Esfahanian在文献[5]中、马明杰在文献[8]中、徐俊明在文献[9]中分别证明了

κ(1)(Qn)=λ(1)(Qn)=2n-2，n≥3;

κ(1)(EHs,t))=λ(1)(EH(s,t))=2s，1≤s≤t;

κ(1)(FQn)=λ(1)(FQn)=2n，n≥4。

我们在文献[10]中证明了κ(1)(FCQn)=λ(1)(FCQn)=2n，n≥4。 本文将探讨交换折叠超立方EFH(s,t)的超连通度和超边连通度,最终确定了κ(1)(EFH(s,t))=λ(1)(EFH(s,t))=2s+2,1≤s≤t。

1 预备知识

一个n元二进制字符串x=xn-1xn-2…x0的第i个字符xi记为x[i]，0≤i≤n-1。

称为x=xn-1xn-2…x0与y=yn-1yn-2…y0的哈明距离。

定义1.1[16]设交换超立方体EH(s,t)=G(V,E)，s,t是正整数。交换超立方体的点集V(EH(s,t))={as-1as-2…a1a0bt-1bt-2…b1b0c|ai,bj,c∈{0,1},0≤i≤s-1,0≤j≤t-1}，交换超立方体的边集E(EH(s,t))={(u,v)| (u,v)∈V(EH(s,t))×V(EH(s,t))}是由三种类型的边E1,E2,E3构成。其中

E1∶u[s+t∶1]=v[s+t∶1],u[0]≠v[0]。

E2∶u[t∶1]=v[t∶1],H(u[s+t∶t+1],v[s+t∶t+1])=1,u[0]=v[0]=0。

E3∶u[s+t∶t+1]=v[s+t∶t+1],H(u[t∶1],v[t∶1])=1,u[0]=v[0]=1。

通过定义1.1，立即可得EH(s,t)的点数|V(EH(s,t))|=2s+t+1，EH(s,t)的边数|E(EH(s,t))|=(s+t+2)2s+t+1，设任意一条边(u,v)∈E(EH(s,t))，则存在唯一确定的i∈{0,1,2,3,…,s+t}使得u[i]≠v[i]且u[j]=v[j]，j=1,2…i-1,i+1,…,s+t. 此时称边(u,v)是i-边。如果EH(s,t)中两个点u和v通过i-边相邻，则称u和v沿维数i相邻。我们也称u是v的i-邻点，记作v=ni(u)。因为EH(s,t)是Qs+t+1的一个子图，所以EH(s,t)是一个二部图。

EH(s,t)中从一个顶点u0出发的路径u0→u1→…→un+1可以由唯一的序列w=(i0-i1-i2-…-in)确定，其中ik∈{0,1,…,(s+t)}。即u1是由与u0关联的i0-边所确定，u2是由与u1关联的i1-边所确定，依此类推。例如，在EH(2,2)中，如果顶点u0=00000，则由w=(2-0-4)确定的从u0出发的路径是00000→00100→00101→10101。

图1 EH(1,2)和EFH(1,2)

EH(1,2)和EFH(1,2)的图(见图1)。

设u∈V(EFH(1,2)).通过定义1.2，如果u[0]=0，则d(u)=s+2，否则d(u)=t+2。

下面给出EH(s,t)和EFH(s,t)的一些结论，主要结果的证明将会用到这些结论。

定理1.1[7]κ(EH(s,t))=λ(EH(s,t))=s+1,1≤s≤t。

定理1.2[16]EH(s,t)同构与EH(t,s)。

定理1.3[17]EFH(s,t)同构与EFH(t,s)。δ(EFH(s,t))=s+1。

通过引理1.2和引理1.3，可以在下面讨论中设s≤t，则δ(EH(s,t))=s+1且δ(EFH(s,t))=s+2。

定理1.4[16]EH(s,t)可分解成两个EH(s-1,t)或两个EH(s,t-1)。

根据EFH(s,t)的定义容易得出EFH(s,t)具有下面两个性质，这两个性质将会简化主要结果的证明。

性质1.5交换折叠超立方体网络EFH(s,t)可以分解成两个子图L和R，其中

V(L)={0as-2…a0bt-1…b0c|ai,bj,c∈{0,1},0≤i≤s-2,1≤j≤t-1}

V(R)={1as-2…a0bt-1…b0c|ai,bj,c∈{0,1},0≤i≤s-2,1≤j≤t-1}

L和R分别是由点集V(L)和V(R)诱导的子图。明显地，L和R都同构于EH(s-1,t)，并且L和R之间的边是由E2和E4构成，记作EFH(s,t)=L⊕R。

性质1.6EFH(s,t)可分解成2t个同构于超立方体Qs的不交子图和2s个同构于超立方体Qt的不交子图。设={Li|Li≅Qs,1≤i≤2t}且R={Rj|Rj≅Qt,1≤j≤2t}

(1)任何两个子图Li与Lm(i≠m)之间是不连边的；同理Rj与Rn(j≠n)之间也是不连边的。

(2)子图Li中的每一个点u在R中都有的两个邻点且这两个邻点是在不同的子图Rj中的；同理子图Rj中的每一个点u在中都有的两个邻点且这两个邻点是在不同的子图Li中的。

(3)Li中不同的点在R中的邻点都位于不同的子图Rj中；同理Rj中不同的点在中的邻点都位于不同的子图Li中。

文献[8]中，作者证明了折叠超立方体FQn(n≥4)中不含3圈，并且任何不相邻的两个点的共同邻点的个数不超过2。因此容易得到下面的引理：

引理1.7交叉折叠超立方体EFH(s,t)中不含3圈，并且任何不相邻的两个点的共同邻点的个数不超过2个。

2 主要结论

定理2.1κ(1)(EFH(s,t))=2s+2,1≤s≤t。

证明首先我们证明κ(1)(EFH(s,t))≤2s+2,1≤s≤t。

设(u,v)∈E2⊆E(EFH(s,t))并且X={u,v},S=NEFH(s,t)-X(X)。根据性质1.6，我们知道由点u,v诱导的图是Qs的一条边。因为EFH(s,t)不含3圈，所以|S|=2s+2。由于|X∪S|=2s+4<2s+t+1，即知S是EFH(s,t)的一个点割。现在我们证明S是EFH(s,t)的一个超点割。设Y=EFH(s,t)-S且w是Y中的一个点。由引理1.7可知，w在S中至多有两个邻点。因此w在Y中至少有s+2-2(≥1)个邻点。因此S是EFH(s,t)的一个超点割，即知κ(1)(EFH(s,t))≤2s+2,1≤s≤t。

接下来我们将证明κ(1)(EFH(s,t))≥2s+2,1≤s≤t。 设K⊆V(EFH(s,t))并且|K|≤2s+1使得EFH(s,t)-K中无孤立点。下证EFH(s,t)-K是连通的。通过性质1.5，可知EFH(s,t)=L⊕R。

设KL=K∩L且KR=K∩R。不失一般性可假设|KL|≥|KR|， 则 |KR|≤s。考虑下面两种情形：

情形 1R-KR是连通的

我们将证明L-KL中的任意一个点u与R-KR是连通的。考虑下面两种情形：

情形 1.1u=0as-2…a0bt-1…b00

图2 定理2.1证明中情形1.1的解释

设Pi是起点为u且由序列wi=(i-(s+t))(i∈{t+1,t+2,…,s+t-1}{k})所确定的路(看图2(a))。即Pi的路径如下：

设Pk是起点为u且由序列wk=(0-1-0-(s+t))所决定的路。即Pk的路径如下：

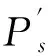
由情形 1.1.1的讨论，又因为EFH(s,t)中不含3圈， 所以下面命题成立。

反应性水肿 对于体重偏重及不爱活动的中老年人来说，夏季是比较难熬的。受高温的影响，他们的皮肤血管会发生扩张，引起动脉血流量增加和毛细血管滤过压增高。此时若久坐不运动，就会导致体液渗透并积聚于皮下组织而肿胀。对此情况，一方面不必太过担心，炎热的夏天一过，自会好转；另一方面，积极减肥和适当运动也会很大程度上避免水肿。

命题2.1存在2s条连接u(或者u0)到R中的某个点的点不交路。

情形1.1.2u0=0as-2…a0bt-1…b01

设Pi是起点为u且由序列wi=(i-(s+t))(i∈{t+1,t+2,…,s+t-1})所确定的路(看图2(b))。即Pi的路径如下：

通过上面的分析下面命题成立。

命题2.2存在s+t(≥2s)条连接u(或者u0)到R中某一点的点不交路。

图3 定理2.1证明中情形1.2的解释

设Pi是起点为u且由序列wi=(i-0-(s+t))(i∈{1,2,…,t}{k})所决定的路(见图3(a))，即Pi的路径如下:

设Pk的路径如下:

u=0as-2…a0bt-1…b01→0as-2…a0bt-1…b00→1as-2…a0bt-1…b00。

设Pi'是起点为u0且由序列wi'=(i-0-(s+t))(i∈{1,2,…,t}{k})所决定的路，即Pi'的路径如下:

通过上面的分析下面命题成立。

命题2.3存在2t+1(≥2s+1)条连接u(或者u0) 到R中某一点的点不交路。

情形1.2.2u0=0as-2…a0bt-1…b00

设Pi是起点为u且由序列wi=(i-0-(s+t))(i∈{1,2,…t})所决定的路(见图3(b))，即Pi的路径如下:

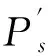
通过上面的分析下面命题成立。

命题2.4存在s+t+1(≥2s+1)条连接u(或者u0)到R中某一点的点不交路。

命题2.3和命题2.4表明了在情形1.2中我们可以找到至少2s+1条连接u(或者u0)到R中某一点的点不交路。因为|K|≤2s+1，所以移除K至多破坏这些路中的2s条，于是一定存在一条连接L-KL中的任意一点u到R-KR中某一点的点不交路，那么EFH(s,t)-K是连通的，因此κ(1)(EFH(s,t))≥2s+2, 即有κ(1)(EFH(s,t))=2s+2,1≤s≤t。

情形2R-KR是不连通的。

通过情形1和情形2的分析，定理2.1成立。

通过EFH(s,t)的定义，我们有ξ(EFH(s,t))=2s+2,s≤t。 在文献[19]中，作者证明了除了星图任何点数超过4的图G有λ(1)(G)≤ξ(G)。因此有λ(1)(EFH(s,t))≤2s+2。定理2.2中若K是一个边集可用同样的方法证明，即可得λ(1)(EFH(s,t))≥2s+2。于是有下面定理成立。

定理2.2λ(1)(EFH(s,t))=2s+2,1≤s≤t。

3 小结

在这篇文章中，我们证明了κ(1)(EFH(s,t))=λ(1)(EFH(s,t))=2s+2,1≤s≤t。

设h是一个正整数，一个图G的h-限制性连通度(h-限制性边连通度)[6，20-21]是G删除G中的某个点子集(边子集)，如果存在这样的子集，使得G不连通且每个分支中点的度数至少是h的最小点集(边集)的基数。容易知κ(0)(G)=κ(G)(λ(0)(G)=λ(G))并且1-限制性连通度(1-限制性边连通度)又称为超连通度(超边连通度)。h-限制性连通度参数是传统连通度参数的一个广义化， 并且它提高了连通度测量的准确性。研究表明如果互连网络有限制性连通度的特性则它是更可靠的并且比其它网络有一个更低的点的容错率，一个自然而有趣的问题是确定κ(h)(EFH(s,t))和λ(h)(EFH(s,t))。