求解凸优化问题的改进对称交替方向乘子法

蒋 峰， 党亚峥

（上海理工大学 管理学院 上海 20093）

1 问题的提出

考虑下面的凸优化问题：

因为经典的ADMM算法难以求得子问题的精确解，为了弥补这一缺陷，何炳生等[4]在x子问题中加入了项，得到了下面的新算法：

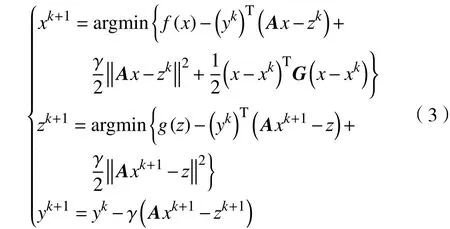
式中，G是一个半正定矩阵。何炳生等[4]证明了该算法的收敛速率。

从问题（1）本身来看，变量x和z是平等的，在设计算法时也希望能够平等对待x和z子问题。因此何炳生等[5]提出了对称ADMM算法，其迭代格式如下：

与原来的ADMM算法不同，式（4）在每一次迭代中更新拉格朗日乘子两次。文献[4]中分析了该算法的全局收敛性，数值计算表明该算法比原始的ADMM算法收敛速度更快。

然而，在很多实际应用中，精确地求解式（4）中的x子问题难以实现，或者要付出很大代价。因此本文提出了一种改进的对称ADMM算法。该算法的主要创新之处是在对称ADMM算法的x极小化子问题中加入半近邻项近似求解此问题，同时给出了收敛性证明。数值计算表明，改进的对称ADMM算法的收敛速度比对称ADMM算法更快。

2 算 法

问题（1）等价于一个变分不等式VI（），求

步骤1给定半正定矩阵G，初始点

步骤2计算

特别地，当G = 0时，算法为对称ADMM算法。

3 收敛性分析

首先，定义几个分析算法收敛性质需要用到的矩阵。

因为G是半正定矩阵，所以等号右侧的第一部分是半正定矩阵，只需证明第二部分也是半正定即可。令

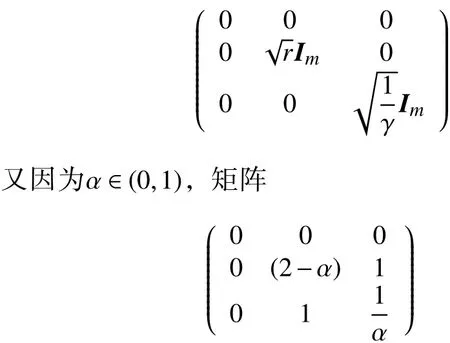
是半正定矩阵，故引理1成立。

引理2 假设H，M，Q是式（6）定义的矩阵，则有

因为

同理，根据z极小化问题的最优性条件，可得

证明 对于同一空间中的向量a，b，c，d和具有适当维度的矩阵H，满足

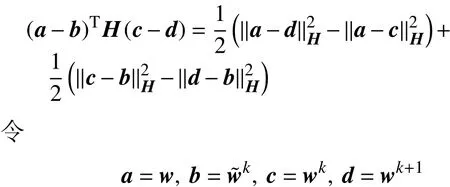
上式可写为

证明 根据式（14）和式（22）得

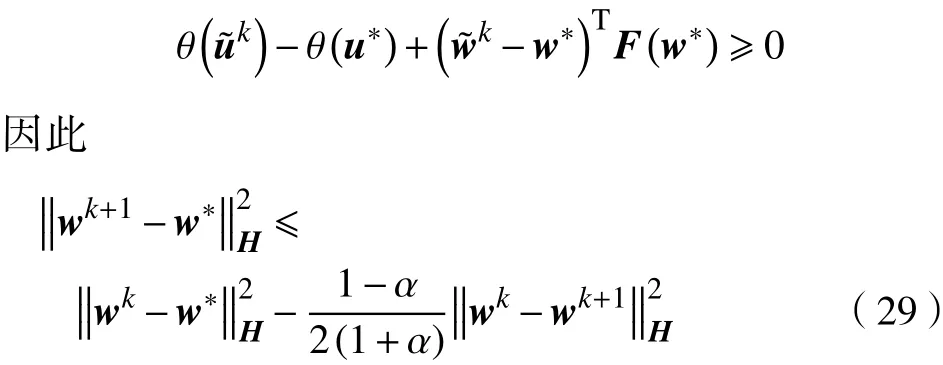
4 数值计算

将改进的对称ADMM算法应用于LASSO问题[6-9]

表1为应用对称ADMM算法和改进的对称ADMM算法解决该问题的结果，其中m表示矩阵P的维数，k表示迭代次数。从表1可以看出，当矩阵P的维数较低时，改进的对称ADMM算法明显快于对称ADMM算法；而当P的维数较高时，对比CPU时间发现，改进的对称ADMM算法的数值表现优势更大。

为了进一步观察两种算法的收敛性，比较了初始残差和对偶残差随迭代次数的变化情况。从图1和图2可以直观地发现，尽管在算法迭代的某些阶段，对称ADMM算法的初始残差、对偶残差减小得更快，但是本文提出的算法先于对称ADMM算法达到收敛条件，因此改进的对称ADMM算法更高效。

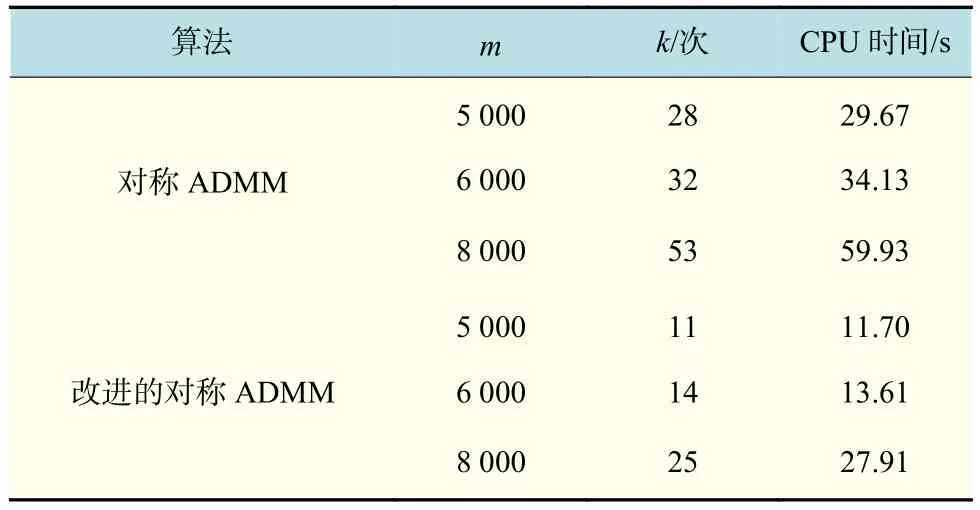
表 1 LASSO问题数值结果Tab.1 Numerical results for LASSO

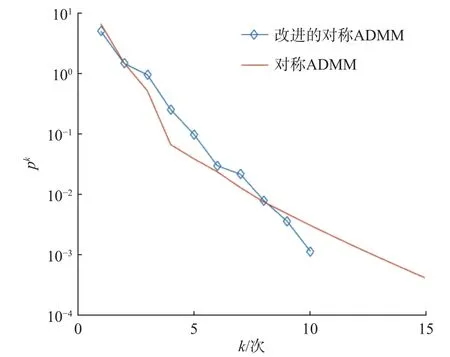
图1 初始残差的变化情况Fig. 1 Evolution of primal residual

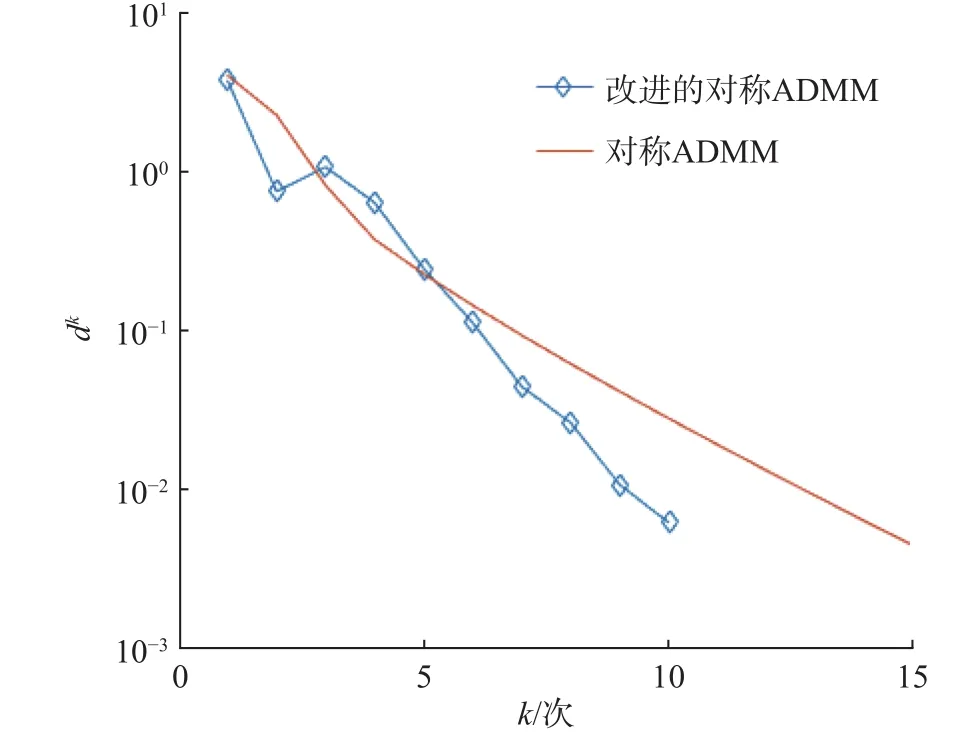
图2 对偶残差的变化情况Fig. 2 Evolution of dual residual

5 结 论

提出了一种求解目标函数具有可分离结构的凸优化问题的改进的对称ADMM算法，并证明了其收敛性。该方法的基本思想是在x子问题中引入一个半近邻项，从而达到加快其收敛速度的目的。数值实验表明，该算法在求解高维的LASSO问题时相对于对称ADMM算法具有明显的优势，但是如何选择最优的还需要进一步研究。