一种加权正交匹配追踪的盲多带信号重建方法

陈明夫， 渠刚荣， 石 磊

（北京交通大学 理学院，北京 100044）

香农采样定理是现代通讯和信号处理的理论基础，它将模拟信号与离散表示法连接起来[1]。对于信号，如果当时，其傅里叶变换的值为0，那么信号被称作-带限的。这里：t表示时间；表示实数域上的Lebesgue平方可积函数空间；表示频率；表示一个常数。香农采样定理说明一个-带限的信号能够从它所有的等步长的采样点准确重建[2]。

本文考虑一类多带信号，其所有的频带都是连续的区间段，且组合一起分布在一个宽的频谱内。信号的重建是在时间区间内进行采样，由这些采样点求出其频谱，通过傅里叶逆变换重建原信号。在采样阶段，如果已知频带位置及其宽度，信号模型就定义了可能输入的子空间。为了在这种情况下进行有效的重建，Landau[3]发展了一种等于带宽和的最小率，它低于相应的Nyquist率，并且对任意一种采样方法都适用。文献[4-5]分别把Landau的方法应用于低率均匀采样和周期非均匀采样，Lin等[6]把范围扩展到多带信号。

盲频谱系统（spectrum-blind systems）意味着既需要盲采样，又需要盲重建。因为在采样之前探测频谱的支集通常不可能或代价太高难以实现，所以研究盲频谱系统非常重要。盲频谱系统在一系列文章[7-9]中被首次提出。这些工作不需要准确的支集，但必须满足一个与多带模型的简单性质没有直接关系的数学条件，即已知占用率的一个上界，占用率定义为支集的勒贝格测度与支集谱跨度（spectral span）的勒贝格测度的比值。甚至当该条件满足时也不能保证准确的重建，因为他们提出的采样率接近Landau最小率。文献[10]中，Mishali等证明了有效的盲重建需要一个更高的采样率。文献[10-11]有相同的性质，即都不需要对频带的位置作限制[9]。Herley等[12]以及Venkataramani等[13]提出一种半盲频谱系统，在这种情况下，信号以一种不依赖于频带位置的多陪集（multi-coset）采样策略进行采样。

压缩感知中的方法力求以次最优性为代价实现易于处理的恢复算法[14-17]，其解决的经典问题是离散且有限向量的恢复。虽然在文献[18-19]中研究了压缩感知结果对连续信号的适应性，但这些论文并没有解决多带信号的情况。

盲多带信号重建的困难一方面在于，各频带的位置是未知的，这意味着取定适当大的频率区间后，该区间内的频谱都需要被恢复，当连续的频谱被适当小的间隔离散后，直接重建要求采样点数等于离散点数，采样代价高。考虑到离散点的幅值大部分是零，可以将其视作特殊的稀疏向量，其中数值不为零的元素聚集成频带数目部分，且每个部分中都没有零元素，因此可以用压缩感知技术以少的采样点来恢复该稀疏向量。以OMP（orthogonal matching pursuit）算法为例，不仅要求观测矩阵满足RIP（restricted isometry property），还要求其 RIC（restricted isometry constant）越小越好。因此，盲多带信号重建的另一方面的困难是采样后得到的矩阵A作为观测矩阵其RIC不够小，无法成功恢复稀疏向量。本文前期工作[20]研究的对象是一般的带限信号，用多次加权的方法改善线性方程组系数矩阵的条件数，提出的加权Landweber方法对理论上严重不适定的带限信号外推有明显的改进，该加权方法可以改善条件数。文献[21]的研究结果证明了条件数越小、RIC也越小，因此，该方法也可以用于压缩感知技术解决盲多带信号重建问题中。

1 盲多带信号重建

根据文献[21]中的定理2，离散间隔取定后，由时域上的采样点可以求出频域上的离散点，然后作傅里叶逆变换得到重建信号，当离散间隔趋于零时，重建信号一致收敛到原信号。对适当大的内的离散化的时候，取满足重建误差范围的适当小的离散间隔，则有

在文献[21]中，王倩等给出定理1和定理2并且证明了：a. 观测矩阵的越小，越小；b. 对于观测矩阵的条件数适当大的情况，基于奇异值分解，对观测矩阵加权得到新的奇异值相同的观测矩阵（此时它的条件数为1）比原观测矩阵有更小的，所以加权后得到的新观测矩阵的RIC小于原观测矩阵的RIC，从而改进了重建的结果。

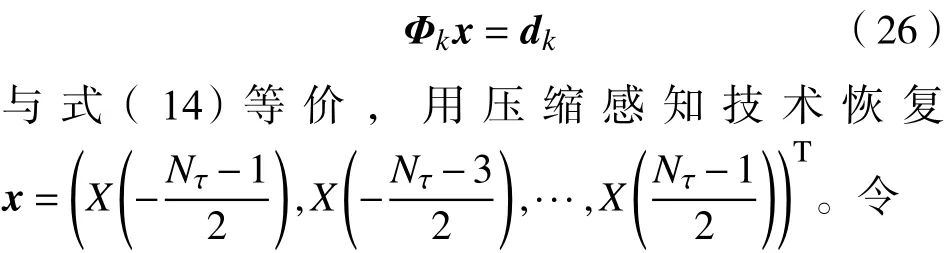
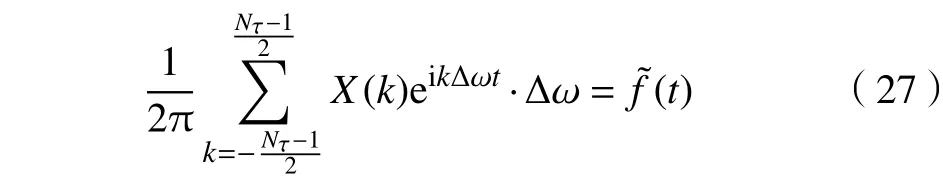
提出一种加权的OMP方法之前，回顾一下OMP算法。

2 数值模拟

模拟的多带信号是

频谱中包含了矩形、三角形、正弦等典型频带，同时它满足定义1。模拟信号在给定频率区间内的频谱如图1所示。模拟中，对适当大的频率区间内的频谱进行离散化时，取满足实际重建误差范围的适当小的离散间隔。离散间隔取定之后，频率区间内的离散点数和幅值非零的离散点数就确定下来。

图1 模拟信号在给定频率区间内的频谱Fig. 1 Spectrum of the simulated signal in a given frequency range

图2 有效重建率随增大的采样区间的变化Fig. 2 Changes of the rate of efficient reconstruction with the increasing size of the sampling interval

图3 有效重建率随增加的采样点数的变化Fig. 3 Changes of the rate of efficient reconstruction with the increasing number of the sampling points

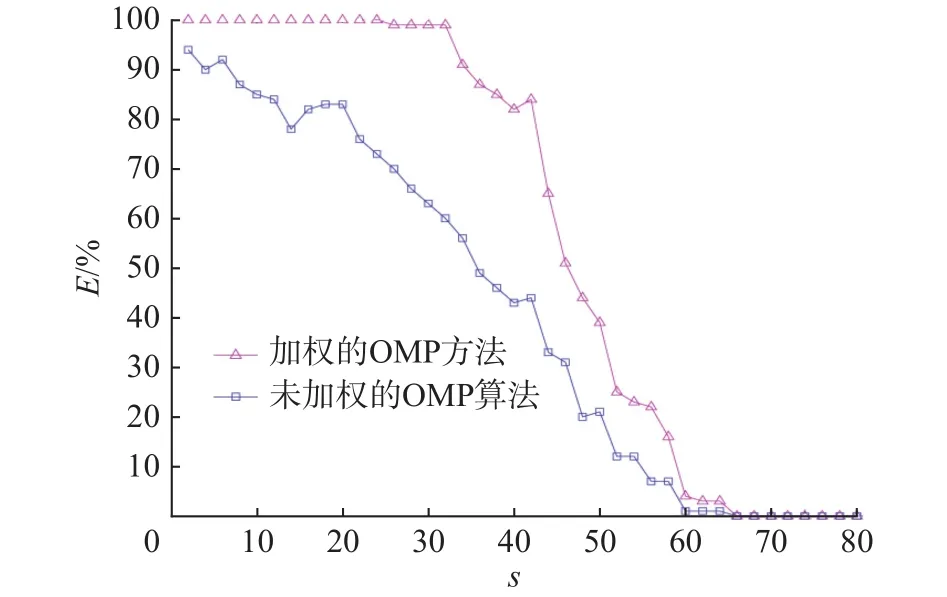
图4 有效重建率随增加的稀疏度的变化Fig. 4 Changes of the rate of the efficient reconstruction withthe increasing sparsity

图2显示，采样点数不变，采样点相同的条件下，加权的OMP方法比未加权的OMP算法有更高的有效重建率。接下来，保持采样区间的大小不变，改变采样点的个数。取，加权次数。

图3显示，采样区间不变，采样点相同的条件下，与未加权的OMP算法相比，加权的OMP方法的有效重建率更高。

本文提出的加权的OMP方法不仅能够用于盲多带信号重建，还能够改善压缩感知中常见的观测矩阵的RIC，改进对一般的稀疏向量的恢复结果。现有的Gaussian随机矩阵、Bernoulli矩阵、Toeplitz矩阵和稀疏随机矩阵都是满足RIP的，模拟结果显示加权OMP方法比未加权的OMP算法有略高一些的有效重建率。为了进一步验证加权的OMP方法的有效性，选择均匀随机矩阵作为模拟的对象，而均匀随机矩阵不满足RIP，其元素独立地服从开区间上的均匀分布。用Matlab生成大小为 160×512的均匀随机矩阵，测量数，信号长度，稀疏信号的支集是随机从的所有大小为的子集中选取的。，，独立同分布地服从标准高斯分布。对于每一个稀疏度，实验重复100次。加权次数。

图4显示，对于不满足RIP的均匀随机矩阵，加权的OMP方法比未加权的OMP算法有明显高的有效重建率。

3 结 论

盲多带信号重建的问题在一定条件下可以用压缩感知技术恢复频域上的稀疏向量后作傅里叶逆变换来解决。根据文献[23]中的定理2，离散间隔取定之后，由时域上的采样点可以求出频域上的离散点，再对其作傅里叶逆变换就得到重建信号，离散间隔趋于零时，重建信号一致收敛于原信号。本文在对频谱进行离散时，取满足重建误差范围的适当小的离散间隔，从而适当大的频率区间内的离散点数和幅值非0的离散点数被确定。研究问题的驱动：一是用尽可能少的采样点得到有效的盲多带信号重建，直接重建要求采样点数等于离散点数，而OMP算法需要采样点数不少于两倍的稀疏度；二是用加权法通过改善观测矩阵的条件数，从而改善其RIC，当观测矩阵因为RIC适当大而不能用于重建时，多次加权后得到的等价观测矩阵只要满足相应的RIC要求就能用于得到有效的重建，这样本文提出的加权的OMP方法比未加权的OMP算法[22]有更高的重建率。由时域上的采样点恢复频域上的稀疏向量的线性方程组可以简化成。如果采样点数非常多，那么由导 出的能够直接计算，因为此时是 一个酉矩阵。通过改善的条件数进而改善的 条件数，把两侧同时乘以一个与有关的加权矩阵，加权过程重复多次。结合加权同样次数的和奇异值分解定理可以得到等价观测矩阵以及等价约束方程。多次加权后得到的新的观测矩阵的条件数变小，其RIC也变小。在模拟阶段，比较加权的OMP方法与未加权的OMP算法的有效重建率。频域上，给定适当大的频率区间，取定满足实际重建误差范围的适当小的离散间隔；时域上，在区间内均匀随机采样。首先，保持采样点的个数不变，改变采样区间的大小。接下来，保持采样区间的大小不变，改变采样点的个数。为了验证加权的OMP方法还能够改善一般的观测矩阵的RIC，用Matlab软件生成大小为160×512的均匀随机矩阵作为观测矩阵，而均匀随机矩阵不满足RIP。因此最后，对于每一个稀疏度模拟100次，每次以同一个均匀随机矩阵，对同一个随机的稀疏向量进行恢复，改变稀疏度。模拟结果验证了同样条件下，加权的OMP方法比未加权的OMP算法有更高的有效重建率。