轴对称图形的研究
代丽冬

摘 要:轴对称图形是一个图形沿一条直线折叠后左右两部分能完全重合的一类图形。本文对轴对称和轴对称图形在定义上进行了研究,阐述了轴对称图形在小学数学中的地位,并对生活中的轴对称图形(包括建筑、动植物、身边实物)的对称理念进行归纳整理。
关键词:轴对称;轴对称图形;教学设计
生活中,我们身边有各种各样的轴对称图形,而在数学学习中,学生在学习轴对称这一知识时总会遇到各种各样的问题,尤其是一部分形象思维不敏感的同学,在观察、寻找轴对称图形和画一个轴对称图形的对称轴时感到无从下手。现行的小学数学教材对轴对称图形这一概念的描述和呈现方式存在一些区别,本文一方面将对轴对称和轴对称图形这两个概念进行阐述,帮助学生充分理解轴对称和轴对称图形之间的异同;另一方面,从生活中常见的轴对称图形和轴对称现象进行举例分析,丰富轴对称在数学课堂中的教学内容。
一、轴对称与轴对称图形的概念
(一)对称图形的定义
对称是指图形或物体对某一点、某条直线或某个平面的反射运动,在形状、大小、长短和排列等方面都相等或相当,具有一一对应关系。
(二)对称图形的分类
在二维空间中,对称分为轴对称(也叫线对称)、中心对称(也叫点对称)两种;在三维立体空间中,除了轴对称、中心对称外,还有面对称。本文主要研究二维空间中的轴对称图形。
(三)轴对称的几种定义
定义1:从图形上的各点做定直线C的垂线并延长一倍,延长线的端点所构成的图形称为与原图形关于直线C成轴对称,称C为对称轴。
定义2:两个图形具有一一变换的关系,如果以每对对应点为端点的线段都被通一条直线垂直平分,那么称这种变换为轴对称(或直线反射),每对对应点互称为对称点,垂直平分对称点所连线段的直线叫做对称轴。
定义3:由一个图形变成另一个图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换,也叫反射变换,简称反射。经变换所得的新图形叫做原图形的像。
(四)轴对称图形的定义
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴。这时,我们也说这个图形关于这条直线(成轴)对称。
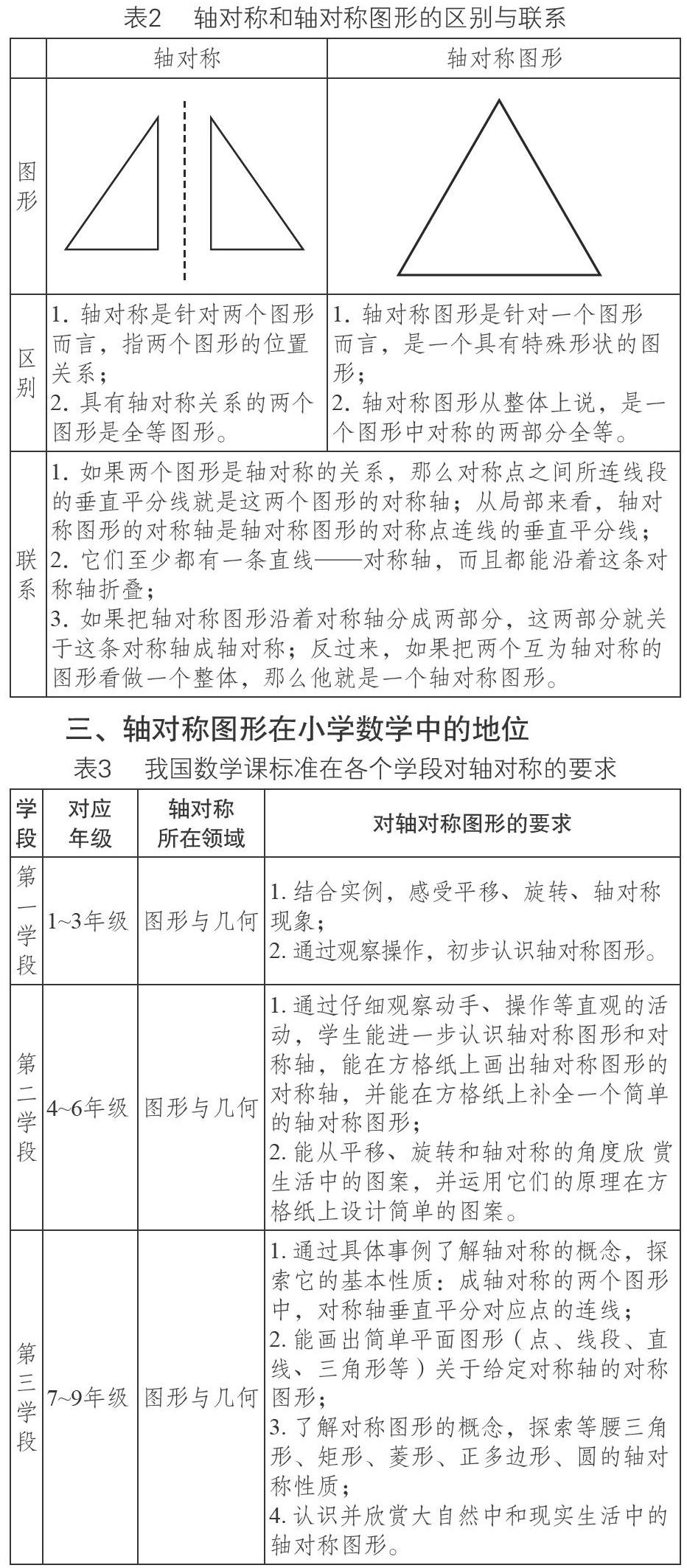
二、轴对称和轴对称图形的区别和联系
三、轴对称图形在小学数学中的地位
从表3可以看出,轴对称图形在学生的每个学习阶段都有涉及,而且难度越来越深,涉及面越来越广。随着年龄的推移,这个学习要求也与范希尔夫妇的几何思维发展阶段相关联,这个发展让学生在学习轴对称图形的过程中难度层层递进,学生在一步步学习中掌握,不至于在学习中无从下手。
四、生活中的轴对称图形
(一)历史建筑物中的轴对称设计
在轴对称教学中我们也会用天安门来进行导入,但会有学生注意到“两边的字不一样,那么算不算轴对称图形呢?”我们如果直观地看天安门的图片,很容易被一些外在因素(两边字样)干扰,但当我们把天安门的建筑框架画下来,就可以很轻易的分辨出它是轴对称图形。
在我们的小学数学课本中,常常使用天安门作为轴对称的引入图案。那么,天安门是不是轴对称图形呢?我们来看一看它的轮廓,如果我们把它画在纸上并沿中间的对称轴折叠,它是能完全重合的。这样类似的建筑还有重庆人民大礼堂、沈阳北陵、消失了的玛雅文化里的墨西哥太阳金字塔等。人们在建设一个建筑物之前,都会对风水、朝向、阴阳八卦等各个方面进行考虑,而轴对称的设计恰好符合了古代的风水考究,也能体现人们对于等级制度的要求。
(二)大自然中的轴对称现象
自然界中的对稱远在人类文明之前就已经存在,所以人类最早期的图形与对称的思考和灵感不排除是直接源于大自然本身。确切地说,人类最初的图形创意与数学思想和几何对称原理很有可能是直接从大自然现象中得到的启发。人类自身的体型就是十分相象的左右对称的典范,以人类为代表的脊椎动物和昆虫类,都明显地具有左右对称的特征。大自然这样的创造,人才能平衡地直立行走,蝴蝶能安然飞翔。但是花草树木的对称图形的呈现,更多地体现了美观大方,这些物体的轴对称图形,更满足大自然的优胜劣汰法则。
(三)生活中的轴对称图形
我们的生活中分布着各种各样的轴对称图形,大到一架飞机的外形,小到一件衣服上的图案,我们都能从中找到对称的现象。飞机的轴对称图形的设计,更利于它在天空中飞翔时保持平衡;而图案的轴对称图形设计更加美观大方,让人能轻易地就记住。
总之,轴对称图形在小学数学中对学生的图形认识、审美能力、几何直观的培养方面意义重大,而且在我们的生活中处处存在轴对称图形,它给我们的生活带来便利(飞机、房屋等),为我们的生活增光添彩,我们要充分利用自己这双发现美的眼睛,随时关注身边的美好,为自己的生活创造美,轴对称图形可以帮助我们创造、发现很多美好的事物。

