高中数学圆锥曲线切线的几何做法

哈尔滨市第三中学 王会书

数学是中小学教育的主要学科之一，理解好数学核心素养与其他素养的关系、数学核心素养有哪些重要的特征，对在中学数学教学中培养学生的核心素养具有重要意义。

正在修订的《普通高中数学课程标准》明确提出了6大核心素养，即数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。这些素养关注学生能力的提高，注重学生的长远发展。

在教材选修2-1第二章《圆锥曲线与方程》这部分内容中，学生在学习过程中面临着很多困难。就高三学生的认知程度而言，部分学生已经能够初步突破圆锥曲线只是注重考察数学运算的认知局限，然而能够直观想象、数学建模、数学抽象才是这部分内容的更高要求。

在圆锥曲线的实际教学中，代数方法解决几何问题、以求代证是复习过程中学生必须掌握的知识和技能，而本质上的几何属性必然会为学生能力上的提升提供帮助。下面就圆锥曲线的切线的几何画法加以探讨。

一、几何法做椭圆的切线

椭圆定义：平面内，到两个定点F1、F2的距离的和为定长2a＞│F1F2│＝2c的点的轨迹称为以F1、F2为焦点的椭圆.

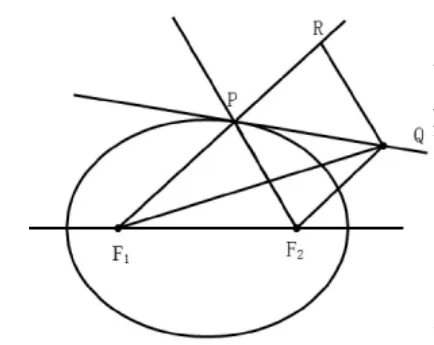
虽然给出了椭圆的标准方程，但我们并不是使用方程进行代数运算.如图直线PQ为焦点三角形△PF1F2的顶角∠F1PF2的外角∠RPF2的平分线，Q为外角平分线上除点P以外的任意一点.我们只需证明│QF1│+│QF2│＞2a，即说明外角平分线上除点P以外的点都在椭圆外部，而点P在椭圆上，故直线PQ就是椭圆在P处的切线.

延长 F1P 至点 R，使得│PR│＝│PF2│，角平分线的几何意义就是对称，连接 QR、QF2，故有△PQF2≌△PQR，连接 QF1，知│QF1│+│QF2│＝│QF1│+│QR│＞│F1R│＝ 2a，说明点Q在椭圆外，由Q的任意性知，外角平分线是椭圆在P处的切线.

由此可以解释椭圆切线的光学性质：如左图，根据例1可得，椭圆在P处的法线是焦点三角形△F1PF2顶角∠F1PF2的内角平分线，从F1点出发的光线，由于入射角∠F1PS等于反射角∠F2PS，故光线照射到椭圆壁上的P点后，被切线PQ镜面反射，所以反射光线必经过另一焦点F2.

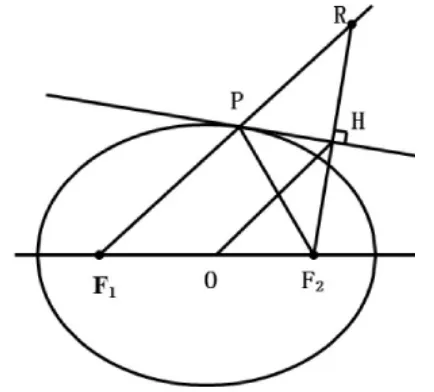
根据例1可得，椭圆在P处的切线即为焦点三角形△F1PF2顶角∠F1PF2的外角平分线，不妨过点F2做外角平分线的垂线，垂足为H，延长F2H交F1P延长线于点R，则有△PHF2≌△PHR，设F1F2的中点为O，知OH为△F2F1R的中位线（│PF1│+│PF2│）＝ a，则点 H 的轨迹是圆，方程为 H：x2+y2＝ a2.

圆 H：x2+y2＝a2称为椭圆 C：＝1（a＞b＞c）上一点 P，请用几何法做出双曲线在P处的切线.

如图，直线PQ为焦点三角形△PF1F2的顶角∠F1PF2的内角平分线，Q为内角平分线上除P以外的任意一点.我们只需证明│QF1│-│QF2│＜2a，即说明内角平分线上除点 P 以外的点都在双曲线外部，而点P在双曲线上，故直线PQ就是双曲线在P处的切线.

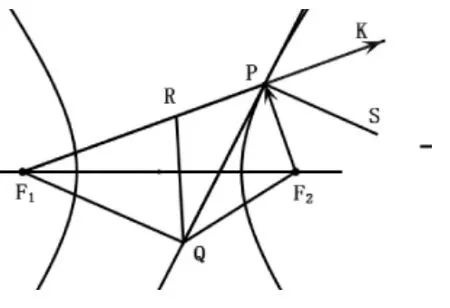
设直线PQ为焦点三角形△PF1F2的顶角∠F1PF2的内角平分线，Q为内角平分线上除P以外的任意一点.在线段PF1上取一点 R，使得│PR│＝│PF2│，连接 QF2、QR、QF1，由角分线的对称性，知△PQF2≌△PQR，│QF1│-│QF2│＝│QF1│-│QR│＜│F1R│＝│PF1│-│PR│＝│PF1│-│PF2│＝2a，即点 Q 在双曲线外，由Q的任意性，知焦点三角形△PF1F2的顶角∠F1PF2的内角平分线即为双曲线在P处的切线.

以上例题可以解释双曲线切线的光学性质：如图，由例3可知，双曲线在P处的法线是焦点三角形△F1PF2顶＝1（a＞b＞c）的准圆，与椭圆相切.

如果从另一焦点向切线做垂线，垂足的轨迹也在圆H：x2+y2＝ a2上.

二、几何法做双曲线的切线

双曲线定义：平面内，到两个定点F1、F2的距离的差的绝对值为定长2a＜│F1F2│＝2c的点的轨迹称为以F1、F2为焦点的双曲线.

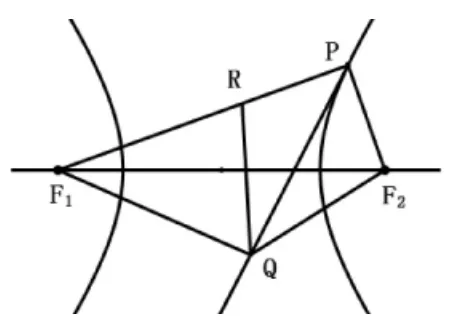
例3已知双曲线C：角∠F1PF2的外角平分线，从F1点出发的光线，由于入射角∠F2PS等于反射角∠KPS，故光线照射到双曲线壁上的点P后，被切线PQ镜面反射，所以反射光线的反向延长线必经过另一焦点F1.

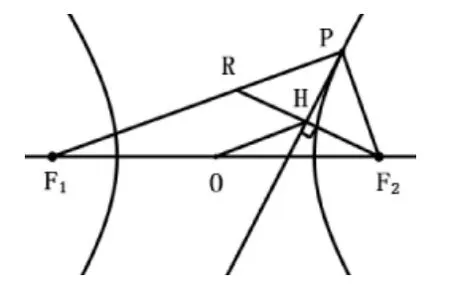
根据例3可得，双曲线在P处的切线即为焦点三角形△F1PF2顶角∠F1PF2的内角平分线，不妨过点F2做内角平分线的垂线，垂足为H，延长F2H交F1P于点R，由角分线的对称性知△PHF2≌△PHR，设F1F2的中点为O，则有（│PF1│-│PF2│）＝a，则H点的轨迹是圆，方程为H：x2+y2＝a2.过另外焦点F1做垂线，轨迹也是圆H：x2+y2＝a2.

圆 H：x2+y2＝ a2称为双曲线 C：＝1（a＞b＞c）的准圆，与双曲线相切.

如果从另一焦点向切线做垂线，垂足还在圆H：x2+y2＝a2上.

三.几何法做抛物线的切线

抛物线定义：平面内到定点F和到定直线l（点F在直线l外）距离相等的点的轨迹，称为以F为焦点，l为准线的抛物线.

例 5 已知抛物线 C：y2＝2px（p＞0）上一点 P，请用几何法做出抛物线在P处的切线.

如图，我们目标还是取∠FPR内角平分线上异于P的任一点Q，只要证明点Q在抛物线外，就说明角平分线上除点P外均在抛物线的外部，直线PQ即为抛物线在P处的切线.

设F为抛物线焦点，连接PF，过P向准线做垂线，垂足为R，由定义知│PF│＝│PR│，设Q为∠FPR平分线上异于P的任一点，连接QF、QR，知△PQF≌△PQR，过点Q做准线的垂线，垂足为 H，在 Rt△QRH 中有│QH│＜│QR│＝│QF│，由定义知，点Q在抛物线外，由Q的任意性知，∠FPR内角平分线是抛物线在P处的切线.

以上例5可以解释抛物线的光学性质：如图，抛物线在点P处的法线为∠FPR的外角平分线，故从F点出发的光线，相当于被抛物线在P处的切线镜面反射，反射光线的反向延长线就是PR，是与x轴平行的.特别的，如果把点光源放在抛物曲面型探照灯的焦点处，探照灯照射出去的是平行于x轴的平行光线，理论上照射的距离可以无限远.

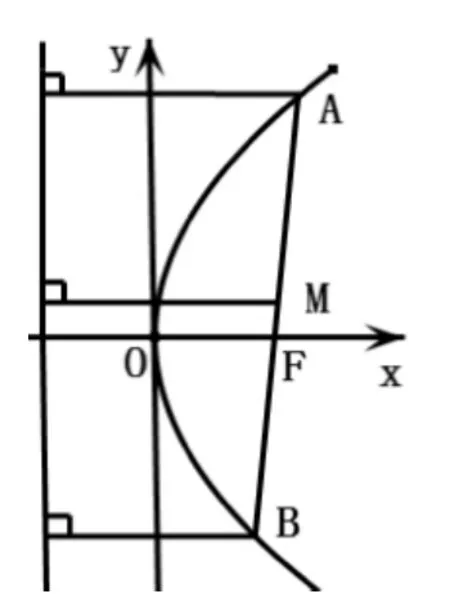
例 6 已知抛物线 C：y2＝2px（p＞0）的焦点为F，过点F的直线l与抛物线交于A、B两点，求证：以AB为直径的圆与准线相切.

过点A、B分别做准线的垂线，垂足为C、D，根据抛物线的定义，知│AF│＝│AC│，│BF│＝│BD│，设线段AB的中点为M，过M做准线的垂线，垂足为N.在直角梯形ACDB中，MN为中位线，则有│MN│＝（│AC│+│BD│） ＝（│AF│+│BF│）＝│AB│，可知圆心M到准线的距离等于半径，即以AB为直径的圆与准线相切，而且切点N也为线段的CD中点.

这一实例也是利用抛物线的几何属性进行证明的，而没有采用通常意义上的方程运算.

例 7 已知抛物线 C：y2＝2px（p＞0）的焦点为 F，过点 F的直线l与抛物线交于A、B两点，求证：抛物线在A、B处的切线互相垂直，并且垂足在准线上.

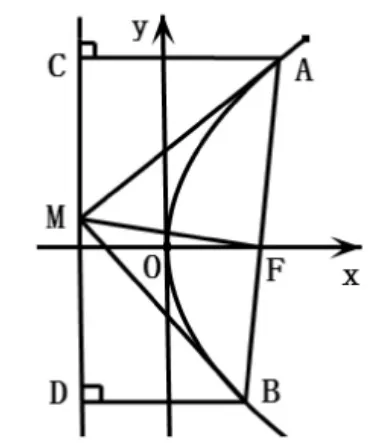
由例5知，抛物线在点A、B处的切线即为∠FAC和∠FBD的内角平分线，不妨先做∠FAC的平分线，找到与准线的交点M，反过来连接点MB，证明MB也是∠FBD的内角平分线，即切线.

过点A、B分别做准线的垂线，垂足为C、D，根据抛物线的定义，知│AF│＝│AC│，│BF│＝│BD│，做抛物线在点A处的切线，即∠FAC的内角平分线，交准线于点M，连接MF、MB，由对称性可得△AMC≌△AMF，知 MF⊥AB，即Rt△BMF≌Rt△BMD，有∠MBF＝∠MBD，即直线 BM为∠FBD的内角平分线，即直线BM是抛物线在B处的切线.

又由│MC│＝│MF│＝│MD│知，M 为 CD 中点.由△AMC≌△AMF和△RtBMF≌Rt△BMD，知∠CMA+∠FMA+∠FMB+∠DMB＝2（∠FMA+∠FMB）＝π，知∠AMB＝，MF⊥MB＝M，且点M在准线上为CD中点.

抛物线还有很多几何性质，在这里就不一一列举了。教师要引导学生学会站在几何性质的角度上思考圆锥曲线问题，而不是一上来就列方程、设直线、代入计算。特别是，这部分内容中有些题目是专门针对圆锥曲线定义和几何性质设置的，用方程计算就把问题复杂化了，有的甚至无法计算出结果.

高三历次考试的试卷中，凡含有解析几何内容的试题，几乎都有考察定义性质的题目。这部分内容学生理解起来比较困难。加强这部分内容的教学，学生的数据分析、数学抽象、数学建模、数学运算、逻辑推理和直观想象等能力都会有不同程度的提高。