C*-代数中的Birkhoff-James正交性
韩婷婷, 刘树冬
(曲阜师范大学 数学科学学院, 山东 曲阜 273165)
1 引言与预备知识
为研究赋范线性空间的结构,学者们引进多种正交性,建立赋范线性空间的几何结构,其中最引人注目的是Birkhoff-James正交性.近年来,学者们关注最多的是有界线性算子的Birkhoff-James正交性,并在研究HilbertC*-模的Birkhoff-James正交性[1]中取得了丰富的研究成果[2-5].但在C*-代数研究中还未能体现其价值,原因在于这方面的研究还很少.本文主要研究C*-代数中的Birkhoff-James正交性,讨论并给出C*-代数中元素Birkhoff-James正交的一些基本性质,同时对C*-代数中正规元与单位元的Birkhoff-James正交给出较好的刻画.
下面给出一些基本概念:
定义1[6]设X为数域K上的赋范线性空间,ξ,η∈X.对任意的λ∈K,若有
‖ξ+λη‖≥‖ξ‖,
则称ξ与ηBirkhoff-James正交,记为ξ⊥Bη.
定义2[7]设A是C*-代数,a∈A.
(1) 若a*=a,则称a为自伴的;
(2) 若aa*=a*a,则称a为正规的;
(3) 设A有单位元I,若存在b∈A,使得ab=ba=I,则称a为可逆的;
(4) 集合σ(a)={λ∈:λ-a不可逆}称为a的谱,r(a)=sup{|λ|:λ∈σ(a)}称为a的谱半径.
众所周知,若a是正规元,则r(a)=‖a‖.
2 主要定理
首先研究自伴元与单位元Birkhoff-James正交的条件.
定理1 设T为C*-代数中的自伴元,则T⊥BI的充要条件是±‖T‖∈σ(T).
证明(a)充分性.由于T是自伴的,故对任意的λ∈,有:
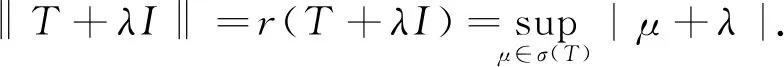
对任意的λ,可分以下两种情况:
(1)当Reλ≥0时,有:
‖T+λI‖≥|‖T‖+λ|=
(2)当Reλ<0时,有:
‖T+λI‖≥|-‖T‖+λ|=
综上可知,T⊥BI.
(b)必要性.若T⊥BI,则对任意的λ∈,‖T+λI‖≥‖T‖.由于T自伴,故‖T‖∈σ(T)或-‖T‖∈σ(T).可分以下两种情况:
(1)若‖T‖∈σ(T),-‖T‖∉σ(T),则存在ε>0,使得σ(T)⊂[-‖T‖+ε,‖T‖].

因此,当‖T‖∈σ(T),-‖T‖∉σ(T)时,T⊥BI不成立.
(2)若-‖T‖∈σ(T),‖T‖∉σ(T),则存在ε>0,使得σ(T)⊂[-‖T‖,‖T‖-ε].
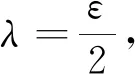
因此,当-‖T‖∈σ(T),‖T‖∉σ(T)时,T⊥BI不成立.
综上可知,T⊥BI不成立.从而±‖T‖∈σ(T).
设E⊂,则称D(E)=sup{|λ-μ|:λ,μ∈E}为E的直径.若T为C*-代数中的元素,则D(σ(T))≤2‖T‖.以下两个推论由定理1容易证明.
推论1 设T为C*-代数中的自伴元,则T⊥BI的充要条件是D(σ(T))=2‖T‖.
推论2 若T为C*-代数中的正元,则对任意的非零实数λ,λT⊥BI不成立.
证明设T为正元,则对任意的非零实数λ,有:
σ(λT)={tλ|t∈σ(T)}⊂{tλ|t∈[0,‖T‖]}.
因为对任意的t1,t2∈σ(T),有:
|t1λ-t2λ|=|t1-t2||λ|≤‖T‖|λ|.
所以
D(λT)≤‖T‖|λ|<2‖λT‖.
从而由推论1知,λT⊥BI不成立.
下面考查正规元与单位元Birkhoff-James正交的情况.
定理2 设T为有单位元的C*-代数中的正规元.若D(σ(T))=2‖T‖,则T⊥BI.
证明由于D(σ(T))=2‖T‖,故存在θ∈[0,2π],使得‖T‖eiθ,‖T‖ei(θ+π)∈σ(T).对任意的λ∈,记λ=|λ|eiθ1.对θ1可分以下两种情况:
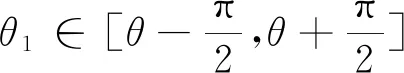
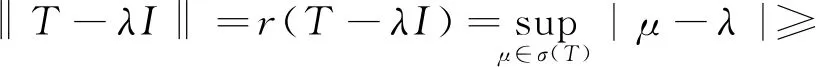

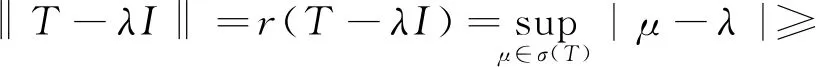
综上可知,若D(σ(T))=2‖T‖,则T⊥BI.
定理2的逆命题不成立.

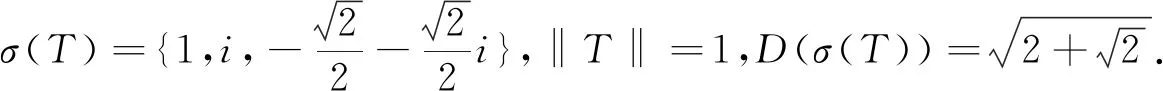
(1)若λ位于第一象限,则
(2)若λ位于第二象限,则
‖T-λI‖≥|1-λ|≥1=‖T‖.
(3)若λ位于第三象限,则
‖T-λI‖≥|1-λ|≥1=‖T‖.
(4)若λ位于第四象限,则
‖T-λI‖≥|i-λ|≥1=‖T‖.
综上可知,T⊥BI,但D(σ(T))≠2‖T‖.
下面讨论C*-代数的单位元与其他元素正交的情况.
定理3 设A为有单位元的C*-代数,T为A中的正规元.若T不可逆,则I⊥BT.
证明对任意的λ∈,有:
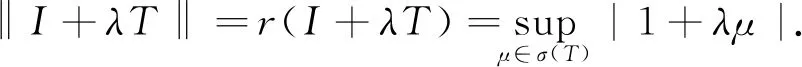
因为T不可逆,所以0∈σ(T),从而
‖I+λT‖≥1=‖I‖.
因此,I⊥BT.
定理4 设A为有单位元的C*-代数,T为A中的正规元.若对任意的λ,存在μ∈σ(T),使得λμ≤0,则I⊥BT.
证明存在0 {reiθ|θ∈[0,2π]}={μ∈||μ|=r}. 对任意的λ=|λ|eiθ∈,取μ=rei(π-θ),则 λμ=|λ|·r·eiθ·ei(π-θ)=-|λ|·r. 由于T为正规元,故 ‖I-λT‖=r(I-λT)= 因此,I⊥BT. 定理5 设T为C*-代数中可逆的正元,则I⊥BT不成立. 证明由于T是可逆的正元,故存在ε>0,使得σ(T)⊂[ε,‖T‖]. ‖I+λT‖=r(I+λT)= 因此,I⊥BT不成立. 推论3 设T为C*-代数中的任意元素,则I⊥BT*T的充要条件为T不可逆. 注设T为C*-代数中的非零元素,则由推论2知,T*T⊥BI不成立.又由推论3知,I⊥BT*T.这说明C*-代数中正元的Birkhoff-James正交性不满足交换律. 定理6 设A为有单位元的C*-代数,T为A中的自伴元.若f,g∈C(σ(T)),则f(T)⊥Bg(T)的充要条件是f⊥Bg. 证明由函数演算的相关结论可知: f(T)⊥Bg(T)⟸⟹任意的λ∈,‖f(T)+λg(T)‖≥‖f(T)‖. ⟸⟹r(f(T)+λg(T))≥r(f(T)). ⟸⟹sup{|f(t)+λg(t)|t∈σ(T)}≥sup{|f(t)|t∈σ(T)}. ⟸⟹f⊥Bg,f,g∈C(σ(T)). 定理7 设A是C*-代数.若a,b∈A,则a⊥Bb的充要条件是a*⊥Bb*. 证明(a)必要性.由于a⊥Bb,故对任意的λ∈,‖a+λb‖≥‖a‖,且有: ‖a+λb‖≥‖a‖=‖a*‖. 因此,a*⊥Bb*. (b)充分性.由于a*⊥Bb*,故对任意的λ∈,‖a*+λb*‖≥‖a*‖,且有: ‖a*+λb*‖≥‖a*‖=‖a‖. 因此,a⊥Bb. 定理8 设A是有单位元的C*-代数,a,b∈A.若u为酉元,则a⊥Bb的充要条件是uau*⊥Bubu*. 证明(a)必要性.由于a⊥Bb,故对任意的λ∈,‖a+λb‖≥‖a‖. 若u为酉算子,则对任意的x∈A,‖uxu*‖=‖x‖,且有: ‖uau*+λubu*‖=‖u(a+λb)u*‖= ‖a+λb‖≥‖a‖=‖uau*‖. 因此,uau*⊥Bubu*. (b)充分性.由于uau*⊥Bubu*,故对任意的λ∈,‖uau*+λubu*‖≥‖uau*‖,且有: ‖a+λb‖=‖u(a+λb)u*‖= ‖uau*+λubu*‖≥‖uau*‖=‖a‖. 因此,a⊥Bb. 定理9 设A,B是C*-代数,a,b∈A,φ∶A→B为满同态.若φ是等距,则a⊥Bb的充要条件是φ(a)⊥Bφ(b). 证明(a)必要性.由于a⊥Bb,故对任意的λ∈,‖a+λb‖≥‖a‖.因为φ是满同态和等距,所以可得: ‖φ(a)+λφ(b)‖=‖φ(a+λb)‖= ‖a+λb‖≥‖a‖=‖φ(a)‖. 从而,φ(a)⊥Bφ(b). (b)充分性.由于φ(a)⊥Bφ(b),故对任意的λ∈,‖φ(a)+λφ(b)‖≥‖φ(a)‖.因为φ是等距的,所以可得: ‖a+λb‖=‖φ(a+λb)‖= ‖φ(a)+λφ(b)‖≥‖φ(a)‖=‖a‖. 从而,a⊥Bb. 定理10 设A,B是单位C*-代数,φ∶A→B为满同态,a1,a2∈A,b1,b2∈B,φ(1A)=1B,‖a1‖=‖b1‖,bi=φ(ai).若b1⊥Bb2,则a1⊥Ba2. 证明由于b1⊥Bb2,故存在ρ∈S(B),使得 因为存在ρ1∈B(A),所以可得ρ1=ρ∘φ,从而ρ1(1)=ρ(φ(1A))=1. 另一方面,因为1=‖ρ1(1)‖≤‖ρ1‖,且‖ρ1‖≤1,所以ρ∈S(A).从而可得: 因此,a1⊥Ba2. 本文通过研究C*-代数中元素的 Birkhoff-James 正交性,得到了一些初步的成果.从结果来看,Birkhoff-James 正交性在C*-代数中成立的条件比较苛刻,也很难刻画.我们注意到谱理论在正交性的刻画中发挥了重要的作用,这或许能为下一步的工作提供一些思路.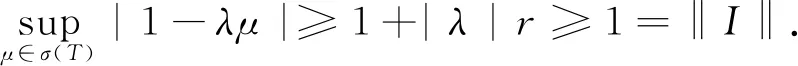
3 结 语

