一个关联指数函数核的Hilbert型不等式
有名辉
(浙江机电职业技术学院 数学教研室, 浙江 杭州 310053)
20世纪初Hilbert提出了著名的Hilbert不等式,至今已有百年发展历史.100多年来,研究者们对Hilbert不等式及其相关形态进行深入探究,取得了很多新成果.这些新成果应用非常广泛,特别是在分析学相关领域有着不可低估的作用[1].通常,Hilbert不等式表述为[2]:
(1)
其中,π是满足式(1)的最佳常数因子.
近年来,通过对式(1)的核函数参数化,并考虑相应的离散形态、半离散形态、高维推广、系数加强,研究者们建立了大量与式(1)有关的新成果[3-12].通过类比演化,大量含有新核函数的Hilbert型不等式也出现在各类文献中.如文献[13]建立了如下齐次核的Hilbert型不等式:
(2)
其中,a>0,β>0,μ(x)=x1-2β,ν(x)=x1+2β.
文献[14]建立了如下非齐次核的Hilbert型不等式:
(3)

在式(3)的基础上,文献[15]通过φ(x)=cscx的有理分式展开,建立了一个全平面上的Hilbert型不等式:
(4)
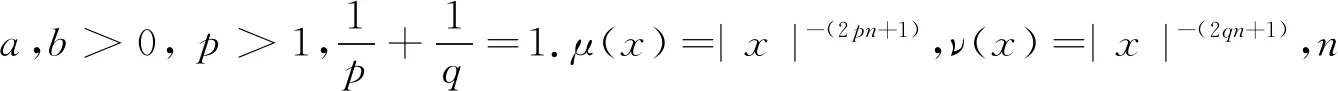
本文构造与指数函数有关的积分核函数,并兼顾齐次和非齐次两种形式,借助统一的处理方法,建立一个类似式(2)、式(3)和式(4)的Hilbert型不等式.
1 定义与引理
定义1 设z>0,记第二型欧拉积分:
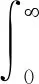
即Γ函数.特别地,当z∈+时,Γ(z)=(z-1)!.
引理1 设b>a>0,η∈{1,-1},λ>0,β>-λ,
K(x,y):=e-a(xyη)λ-e-b(xyη)λ,
记
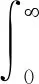
(5)
则
(6)
证明若β=0,对任意的η1,η2>0,利用简单的变量代换,并借助积分第一中值定理,得:
其中,a<ξ1,ξ2 (7) 若β≠0,则由分部积分得: (8) 由式(7)、式(8)得式(6)成立. 引理1证毕. 引理2 设b>a>0,η∈{1,-1},λ>0,β>-λ,定义 Dη:={x:x>0,xη<1}, 且 K(x,y):=e-a(xyη)λ-e-b(xyη)λ, 则当n→时,有: (9) 证明作变量代换xyη=u,由Fubini定理可知: 令n→,并利用式(5),得: 定理1 设b>a>0,η∈{1,-1},λ>0,β>-λ,μ(x)=xp(1-β)-1,ν(x)=xq(1-ηβ)-1,f(x),g(x)≥0,且满足f∈Lp,μ(+),g∈Lq,ν(+),K(x,y):=e-a(xyη)λ-e-b(xyη)λ,则 (10) 其中,C(a,b,λ,β)由引理1定义,且是满足式(10)的最佳常数因子. 证明根据Hölder不等式,得: (11) 其中, 根据引理1,得: (12) 及 (13) 把式(12)和式(13)代入式(11),得: (14) 若式(14)中等号成立,则必有不全为零的实数A与B,满足[16] 即 Axp(1-β)fp(x)=Byq(1-ηβ)gq(y)a.e.于+×+. 那么有常数C,使得 Axp(1-β)fp(x)=C,a.e.于+, 且 Byq(1-ηβ)gq(y)=C,a.e.于+. 不妨假设A≠0,则 这与f∈Lp,μ(+)矛盾.故式(14)不取等. 下面证明式(10)中的常数因子是最佳值. 事实上,如果此常数因子不是最佳值,一定存在实数0 (15) (16) 把式(9)的结果代入式(16),并令n→,则k≥C(a,b,λ,β),显然矛盾.故式(10)中的常数因子是最佳值. 定理1证毕. 在定理1中,令η=1,λ=1,则有: 推论1 设b>a>0,β>-1,μ(x)=xp(1-β)-1,f(x),g(x)≥0,且f∈Lp,μ(+),g∈Lq,μ(+),则 (17) 其中, 是满足式(17)的最佳常数因子.另外,若令η=-1,λ=1,则可得到一个类似的齐次核的Hilbert型不等式. 通过引入多个参量,借助经典分析技巧,建立了一个关联指数函数核的Hilbert型积分不等式.从研究内容上看,文中所建立的结果是前人已有成果的一个补充.从研究方法上看,文中统一了齐次核与非齐次核的构造.这些均具有一定的创新价值.
2 主要结果
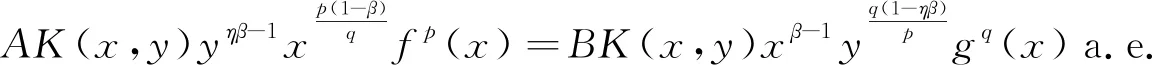
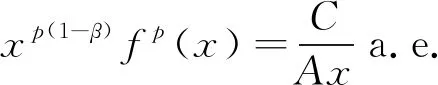
3 结 论

