改进的Boussinesq方程的精确行波解及其波形随波速的演化

李韶伟

（台州学院 电子与信息工程学院，浙江 台州 318000）

0 引言

众所周知，对非线性发展方程行波解的研究在非线性物理现象研究中具有重要的意义。人们已经找到了许多方法［1-8］用于求解非线性发展方程，首次积分法［9-12］就是其中一种非常有效的求解方法。

改进的Boussinesq方程［13］

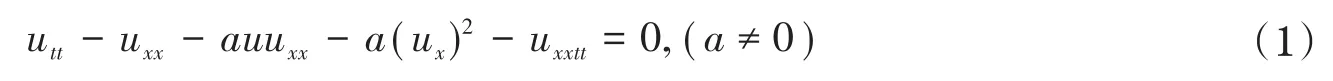
是一个重要的物理和流体力学模型。它从流体力学的方程组中得到，可以用来描述波在磁场中的传播，可以代替“坏”Boussinesq方程［14］

文献［15］考虑了方程（1）的 painlevé 性质；文献［16］得到了方程（1）的如下解

其中v为波速。在特殊的参数条件a=1时，文献［1］得到了方程（1）的7个精确解。本文求解得到了方程（1）更简洁的精确解表达式，同时分析得到了解随能量q和波速v的演化特性。

1 方程（1）的解

对方程（1）做行波变化令u=u(ξ)，ξ=x-vt，并积分两次（此处假设u(n)(ξ)→0,|ξ|→∞（n=1，2，3，4），且渐近值满足方程，可以得到简化的常微分方程：

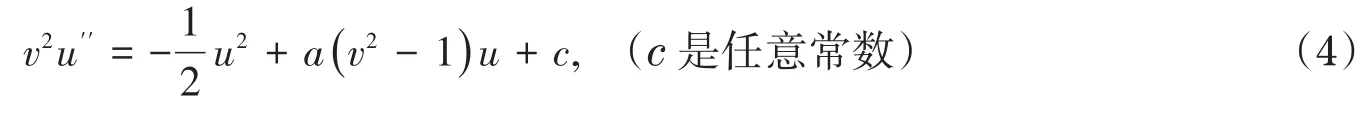
做变量替换，令

可将方程（4）转化为

将方程（6）化成等价的平面动力系统

根据平面动力系统理论，我们得到系统（7）相图，如图1所示，

图1 系统（7）的相图

系统（7）是一个保守的Hamilton系统，其Hamiltonian能量为

利用首次积分法，我们可以得到

其中f(X)=X3-3pX+2q。

通过分类讨论，可以得到了系统（7）相应的四类行波解：

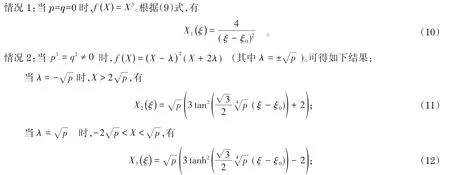
2 解的演化关系

根据上述求解结果，我们分析得到了方程（1）的解关于Hamilton能量q和波速v的演化结论。

2.1 解随能量q的演化

当p＞0时，随着参数q从-∞到+∞的变化，方程（1）的解从情况3→情况2→情况4→情况2→情况3演化；

当p=0时，随着参数q从-∞到+∞的变化，方程（1）的解从情况3→情况1→情况3演化；

当p＜0时，无论参数q为何值，方程（1）的解均属于情况3。

如图2所示，取p=1，a=1，v=2，我们给出了周期波解u6(ξ)和钟状孤波解u3(ξ)的图形，并以此来展示当p＞0时的方程（1）的解随参数q的演化过程。

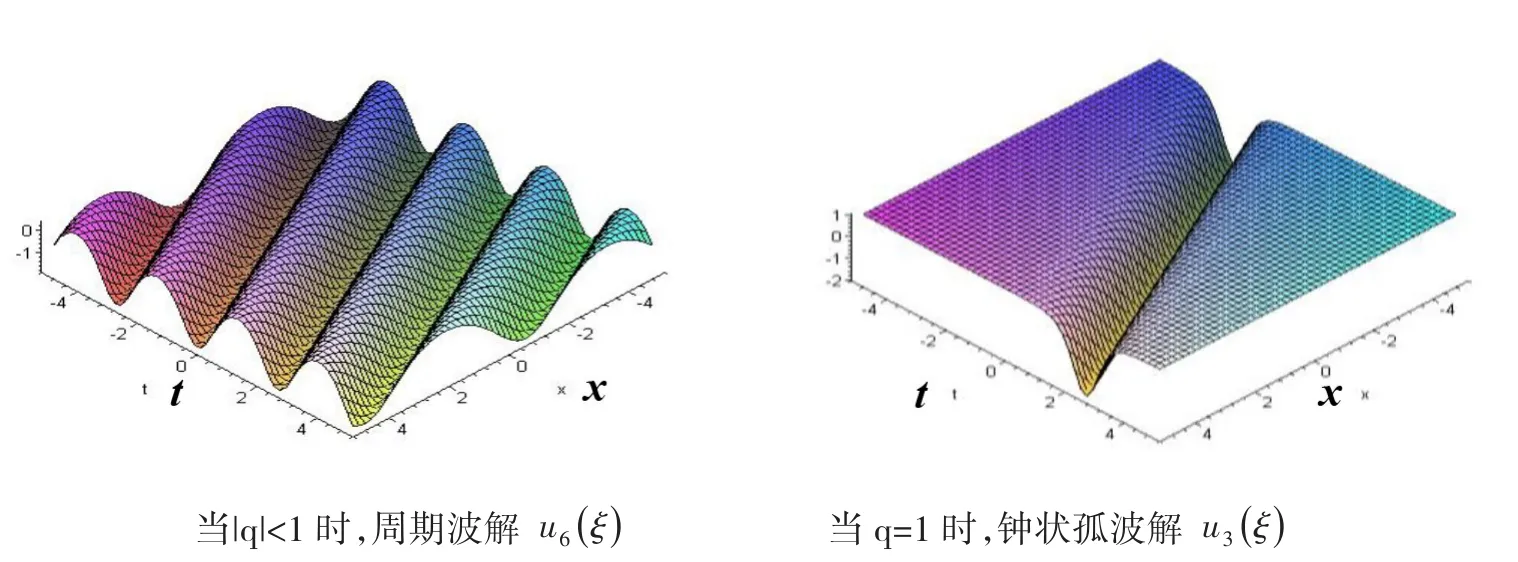
图2 解随Hamilton能量q演化的图形

2.2 解随波速v的演化

进一步的，我们发现了这些解（式（17））随行波速v变化的相关特性。以q＞0为例。

根据p3和q2之间的关系和式（6）中p的表达形式，我们得到如下关系式

根据情况1～情况4的参数条件，我们分析得到如下结论：

在满足1+2ac≤0的条件下，若v2＜V+，方程（1）的解为u5(ξ)；若v2=V+，方程（1）的解为u3(ξ)和u4(ξ)；若v2＞V+，方程（1）的解为u6(ξ)和u7(ξ)。

显而易见，u3(ξ)是方程（1）的有界的钟状孤波解，而u6(ξ)是方程（1）的有界的周期波解。上述结论展示了方程（1）的解u6(ξ)和u3(ξ)存在着随着波速v的变化而连续演化的关系。我们给出四组仿真的u6(ξ)和u3(ξ)图形展示这样的波形随波速的演化关系：

1）如图3所示，取a=1,c=0,，当v2→V0时，u6（ξ）→u3（ξ）。

图3 当v2→V0时的u6（ξ）→u3（ξ）

2）如图4所示，取a=1,c=0,，当v2→V_时，u6（ξ）→u3（ξ）。

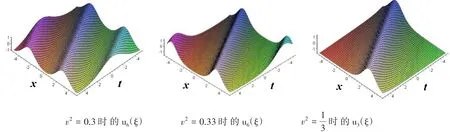
图4 当v2→V-时的u6（ξ）→u3（ξ）

3）如图5、图6所示，取a=1,c=0,和V+=2。

图5 当v2→V-时的u6（ξ）→u3（ξ）

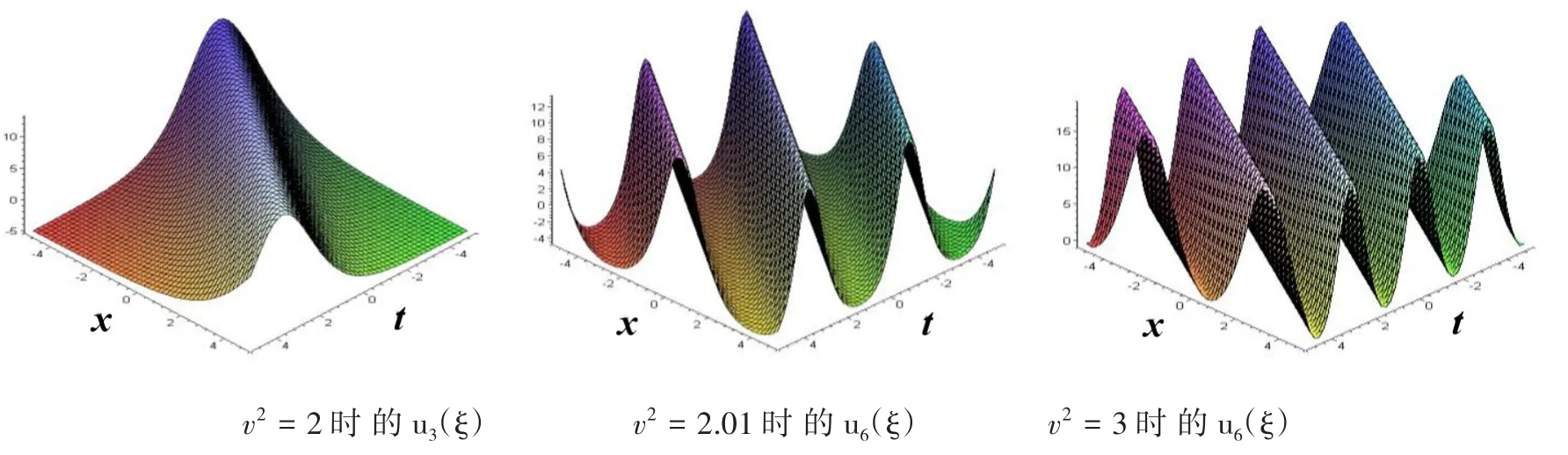
图6 当v2→V+时，u6（ξ）→u3（ξ）

4）如图7所示，取a=1,和V+=3，当v2→V+时，u6（ξ）→u3（ξ）。

图7 当v2→V+时的u6（ξ）→u3（ξ）

3 结语

根据平面动力系统，式（17）所得解均为方程（1）的解，其中u3(ξ)是其唯一的有界钟状孤波解，而u6(ξ)是其唯一的一类有界周期波解。u6(ξ)和u3(ξ)之间关于波速v存在连续的演化关系。本文所得到的解（式（17））比文献［1］中的简洁，其中式（3）所表示的解u3(ξ)与文献［16］所述一致。与此类似，文中从式（6）至式（16）的分析求解过程以及解可被用于其他方程例如Klein-Gōrdon方程，Sine-Gorden方程和Dodd-Bullough-Mikhailov 方程等的求解［17］。通过求解（6）式，上述方程的行波解也可由式（10）～（16）表达。