AlN对Mg-Al合金凝固过程影响机制的价电子理论研究

张爱民，韦佳宏，马秉馨，张 倩，陶 凯，冀盛亚

AlN对Mg-Al合金凝固过程影响机制的价电子理论研究

张爱民1,2，韦佳宏3，马秉馨1，张 倩1，陶 凯1,2，冀盛亚1,2

（1．河南工学院 材料科学与工程学院，河南 新乡 453003；2.河南省金属材料改性技术工程技术研究中心，河南 新乡 453003；3.河南工学院 电气工程与自动化学院，河南 新乡 453003）

采用固体与分子经验电子理论（EET）研究AlN对Mg-Al合金凝固组织的影响机理，建立了Mg、AlN晶体结构的计算模型，利用自洽键距差法（SCBLD）计算了Mg、AlN晶体的价电子结构与结合能。在此基础上，采用断键法计算了Mg、AlN晶体(0001)晶面的表面能，进而计算了Mg/AlN异质界面上的界面能。研究结果表明：Mg/AlN之间的界面能大于Mg自身均匀形核时的固/液界面能，因此，熔体中的Mg原子不能依附于AlN(0001)晶面进行生长，AlN对Mg-Al合金的细化效果不明显，这从电子层次上解释了AlN在Mg-Al合金凝固过程中的微观作用机制。

AlN；EET；自洽键距差法；价电子结构；结合能

0 引言

镁合金具有密度低、比强度高、易切削加工等优点，被称为“21世纪绿色工程材料”，在航空航天、3C电子等领域均有大规模应用[1-3]。镁合金中应用最广泛的是Mg-Al系合金，与铸态铝合金类似，Mg-Al合金在常规条件下的凝固组织较为粗大，力学性能较低，生产中需要进行晶粒细化处理。目前，Mg-Al合金最主要的晶粒细化方法是向熔体中添加含碳物质，即碳质细化法，但向Mg-Al合金熔体中添加碳或含碳的物质时会严重污染环境且存在与合金熔体不润湿等问题[4]。因此，开发不含碳的细化剂是解决此问题的有效路径之一。

晶格错配度是目前异质形核的基本理论判据，根据异质形核的晶粒细化机理，AlN与Mg的晶格错配度较小，理论上可作为Mg的异质形核核心[5]。然而经过试验发现，一些满足晶格匹配度的异质相的细化效果并不稳定，甚至存在与该理论相悖的试验现象。比如，TiB2与α-Al之间的晶格错配度仅为4.22 %，但在没有多余溶质Ti的参与下，单独的TiB2并不能细化纯铝晶粒[6]；Al8Mn5与Mg的晶格错配度也不能满足形核要求，但在一定条件下仍可较好地细化Mg-Al合金的晶粒尺寸[7]。由此可见，把晶格错配度作为异质形核的理论判据是不充分的，晶格错配度并不是异质形核的本质要求。异质形核能力的大小取决于形核基底与基体相之间界面能的强弱，而影响界面能的因素除了基底与基体相的晶格错配度外，还包括基底的尺寸、外露表面的取向与熔体中原子的相互作用等，所以对异质形核理论的认识不应局限于基底与基体相之间的晶格错配度。

因此，本文基于EET电子理论对AlN、Mg进行价电子结构分析，并计算出AlN、Mg的结合能，在此基础上计算Mg、AlN（0001）晶面的表面能，给出二者之间的异质界面能，从电子层次深入研究AlN对Mg-Al合金凝固组织的作用机理，这对于完善异质形核的细化机制以及开发新型Mg-Al合金非C晶粒细化剂都具有重要的理论意义和实用价值。

1 计算方法与结果

1.1 Mg、AlN价电子结构的计算

在自洽键距差（SCBLD）方法中，进行计算的前提条件是必须知道体系内原子的空间排布，对晶体来说就是要知道晶体结构的类型、晶格常数和原子的位置坐标。Mg的晶体结构类型为密排六方结构（hcp），空间群是P63/MMC，空间群号是194，原子等效点位置为（1/3,2/3,1/4; 2/3,1/3,3/4），单胞内有2个Mg原子，晶格常数为=0.32030 nm、=0.52002 nm[8]；AlN的晶体结构类型同为密排六方（hcp），空间群是P63mc，空间群号是186，单胞内有2个Al原子和2个N原子，晶格常数为=0.3112 nm、=0.4981 nm。原子等效位置为（1/3,2/3,z; 2/3,1/3,1/+z）。原子位置及坐标分别为Al1，2b，（1/3,2/3,0）；Al2，2b，（2/3,1/3,0.5）；N1，2b，（1/3,2/3,0.3869）；N2，2b，（1/3,2/3,0.8869）[9]。根据以上参数，可以分别建立Mg、AlN晶体结构的计算模型，如图1所示。

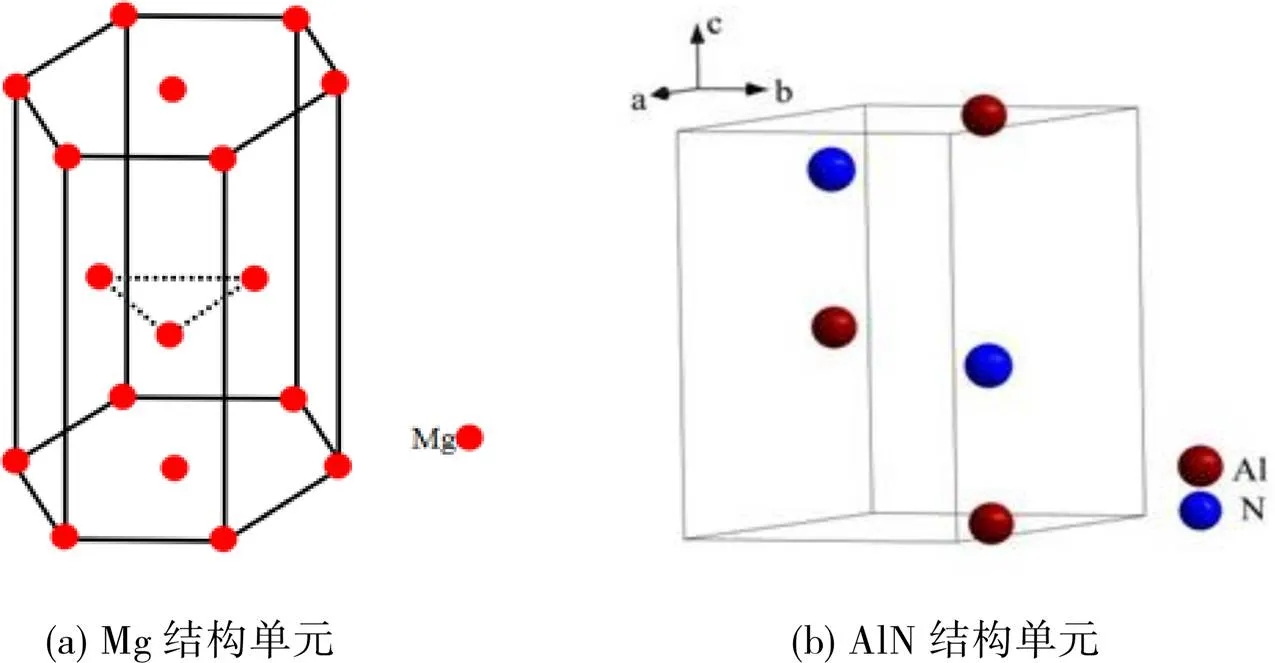
图1 Mg、AlN的价电子结构分析模型

下面以Mg的价电子结构计算为例，给出计算步骤。首先，根据EET的基本假设一给出Mg的态和态：

对于态：=2，=0，=0，=0。

对于态：l=1，m=1，n=1，τ=1。

根据EET的基本假设二，把各个参数代入公式[10]及相关的公式，可以得到Mg的4个杂阶，如表1所示。同理，可得出N、Al的杂化态，示于表2、3 中。

表1 Mg的杂化表

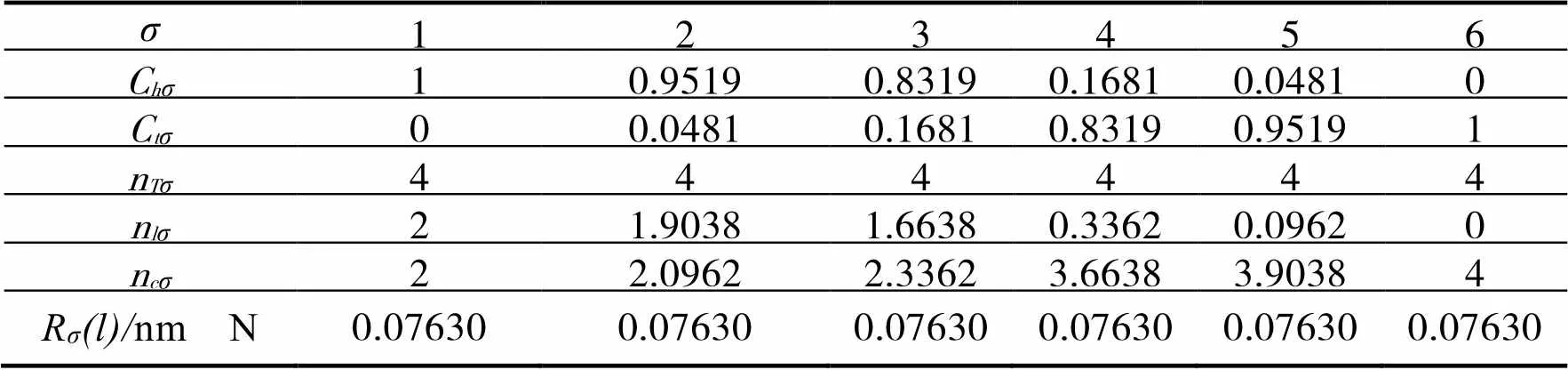
表2 N的杂化表

注：其中=2，=2，=0，=0；=1，=3，=0，=1，=14。

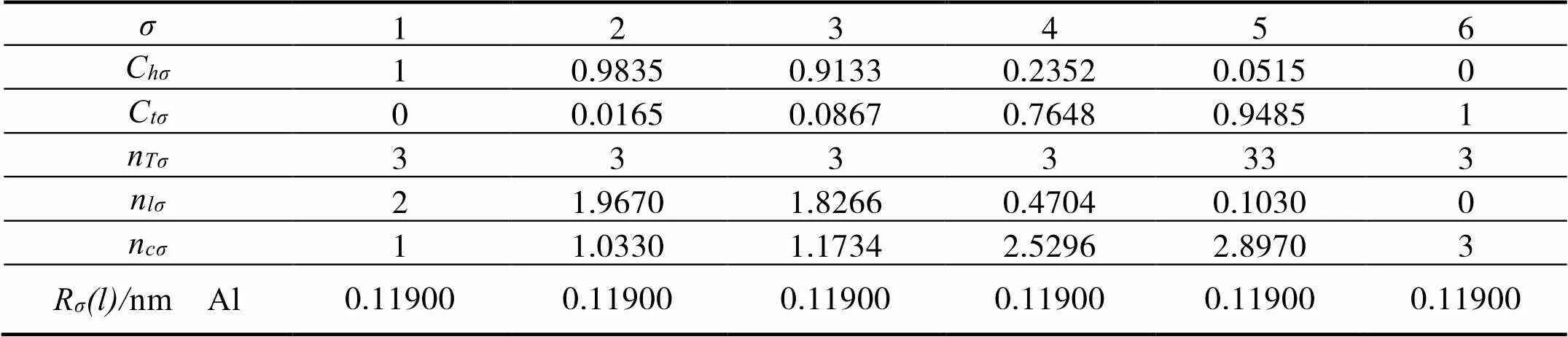
表3 Al的杂化表

注：其中=2，=1，=0，=0；=1，=2，=0，=1，=13。

由图1可知，在Mg的晶胞中有5种不可忽略的共价键，利用立体几何中两点间的距离公式可以计算出这些键的实验键距和等同键数。实验键距分别为：

等同键数的公式为：

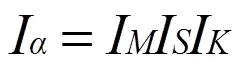
其中I表示在一个分子或晶体的结构单元中，选取成键两个原子的一个为参考，这个原子在单胞中总的数量；I表示一个参考原子在晶体内形成的所有等同键的数目；I是一个参数，当成键的两原子为同类原子时其值为1，为不同原子时其值为2。由此可得各个等同键数为：

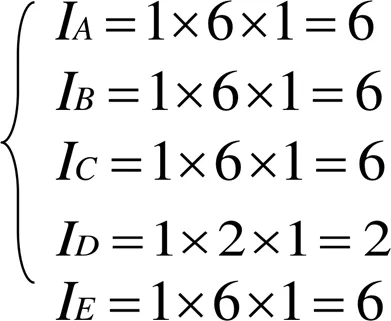
Mg的晶胞中A、B、C、D、E键上的键距表达式为：

由式（4）中第一个式子与其他各式相减，可得式（5）

在研究的晶体内，单位晶胞内的共价键络上的电子总数应该与这个单位晶胞内原子的所有价电子数相等。因此，n还可表述为：

其中，n是单位晶胞内的价电子总数，等于所有共价键上分布的电子总数，代表的是最强共价键上的电子对数。联合公式(5)和公式(6)可计算出共价键上的电子对数。

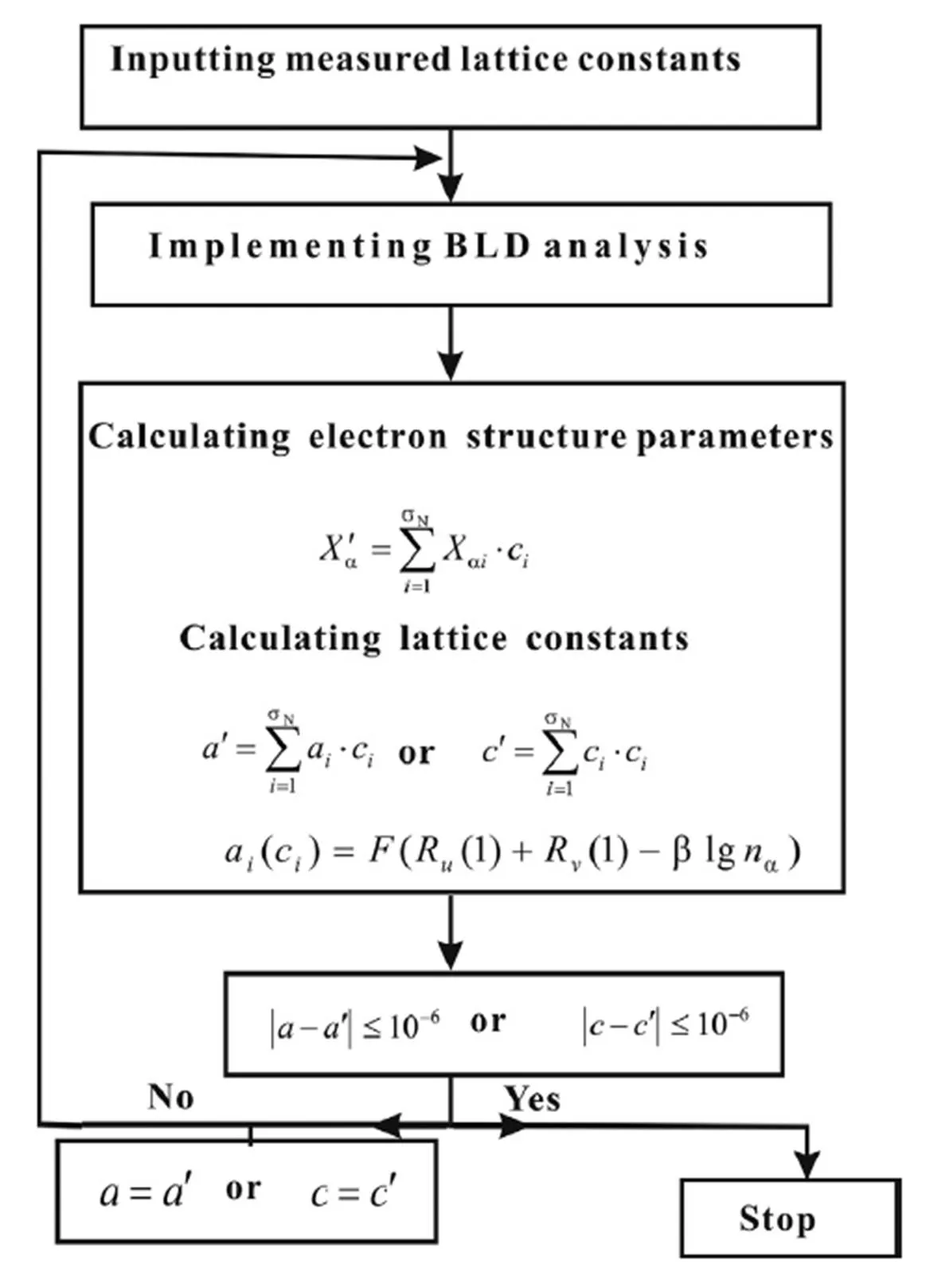
图2 SCBLD法的运算流程图[11]

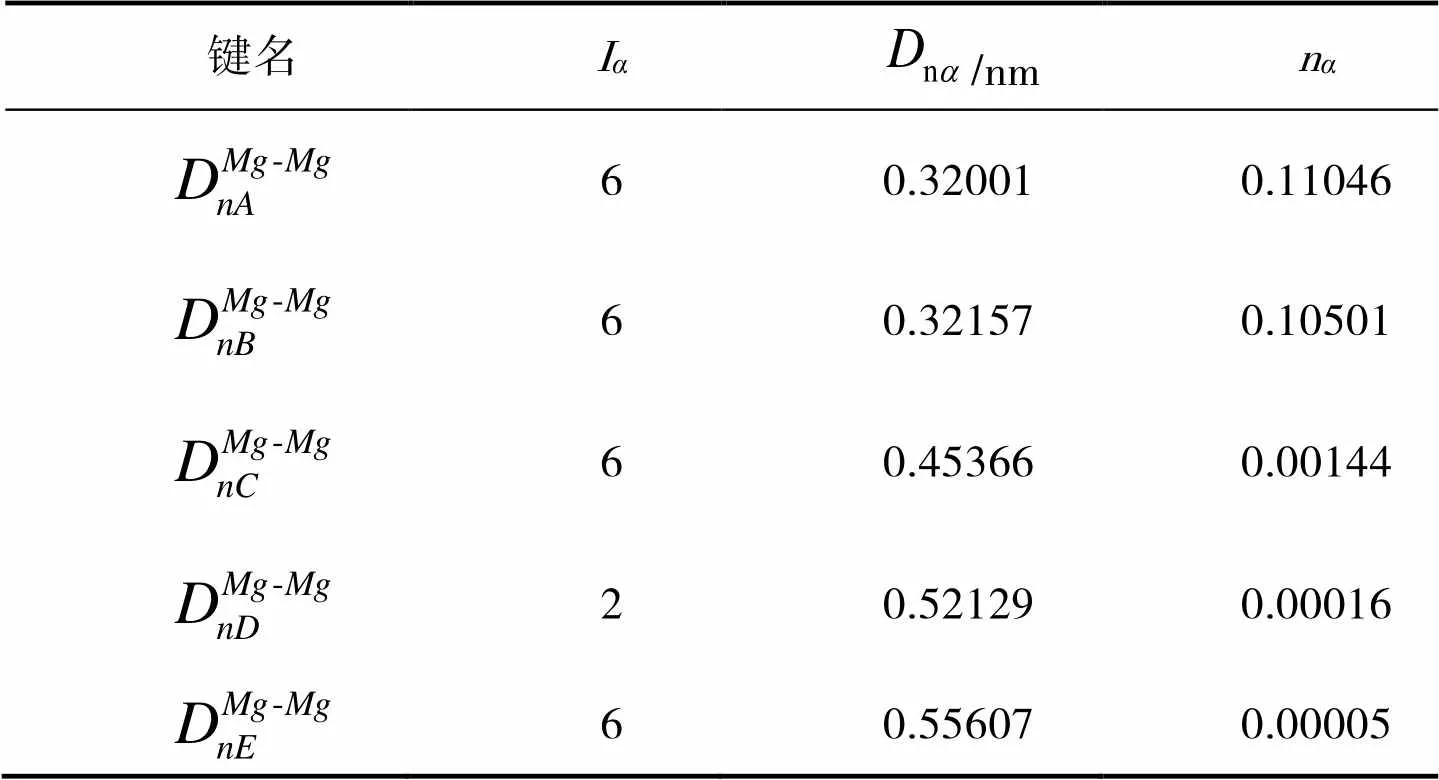
表4 Mg的价电子结构

表5 AlN的价电子结构

1.2 Mg、AlN键能与结合能的计算

根据EET理论，在价电子结构计算的基础上, 可以进一步计算出Mg、AlN的共价键键能与晶体结合能。键能计算公式如下：

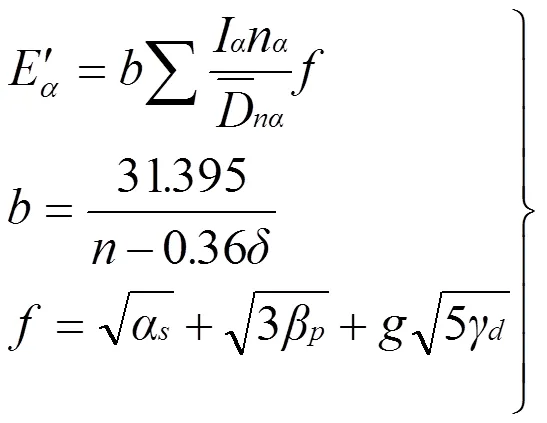
公式(7) 中计算参数的具体含义详见文献[12]。

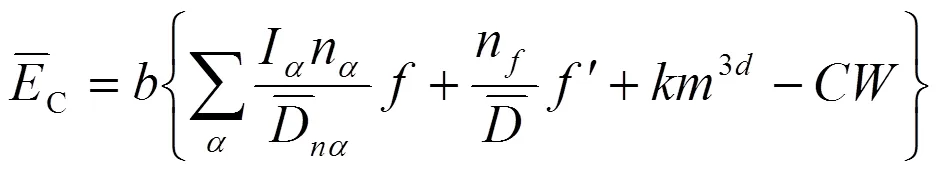
公式(8)中计算参数意义与求解过程仍可参考文献[12]。

针对EET多重解的问题，还需根据文献[13-15]中的如下公式计算出Mg、AlN结合能的统计值：

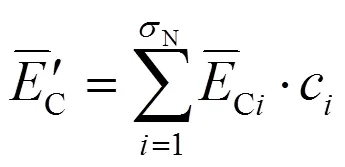
其中的计算参数同样在文献[12]中给出。将Mg、AlN晶体优化后得到的晶格常数和值及其他相关参数代入公式(7-9)即可计算出Mg、AlN的键能与结合能，Mg、AlN的计算结果分别示于表6、表7。

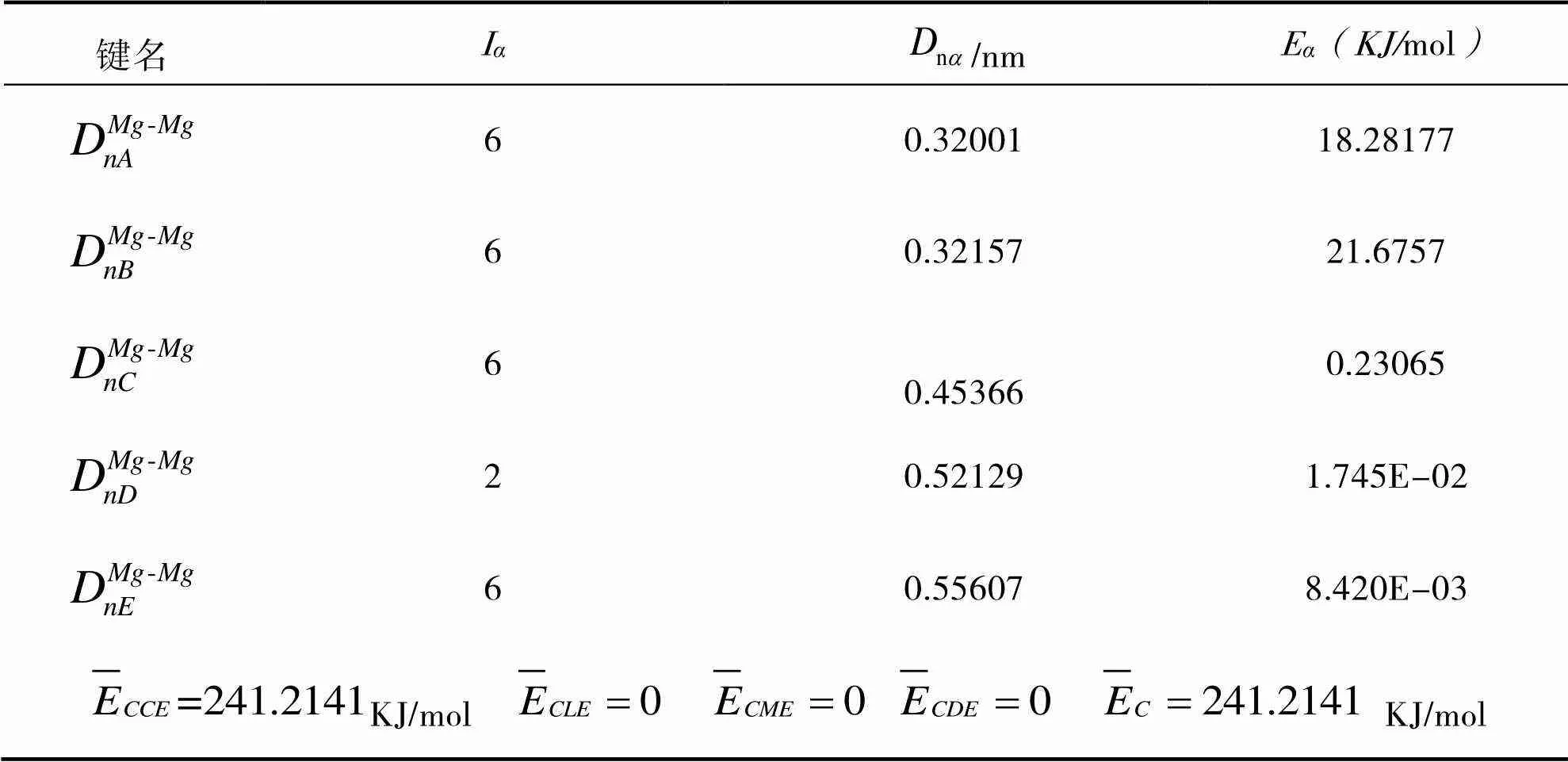
表6 Mg各键的键能与结合能

表7 AlN各键的键能与结合能

1.3 Mg、AlN（0001）晶面的表面能与Mg/AlN之间的界面能

一般认为表面能是由表面原子的共价电子所决定的，Mg熔体内的AlN一般是内生的，其表面原子的排列仍可按原来的晶体结构看待。EET中，晶体表面能的大小可认为是两晶面间所有共价键键能之和的一半，因此，计算晶体某一晶面的表面能时，只需计算两晶面间的共价键键能之和。文献[16]指出晶体物质在形成表面时，其表面上存在着断键，本文根据文献[17]提出的断键分析法来计算AlN、Mg表面在(0001)晶面终止时的表面能。

断键分析法首先定义了等同断键数Xα，其与EET中的等同键的定义相同，即在晶体表面上由同样原子形成的键长和键能相同的等同键被破坏后所形成的断键数，计算公式为：

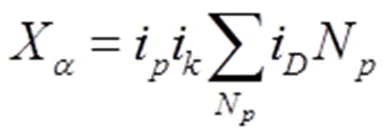
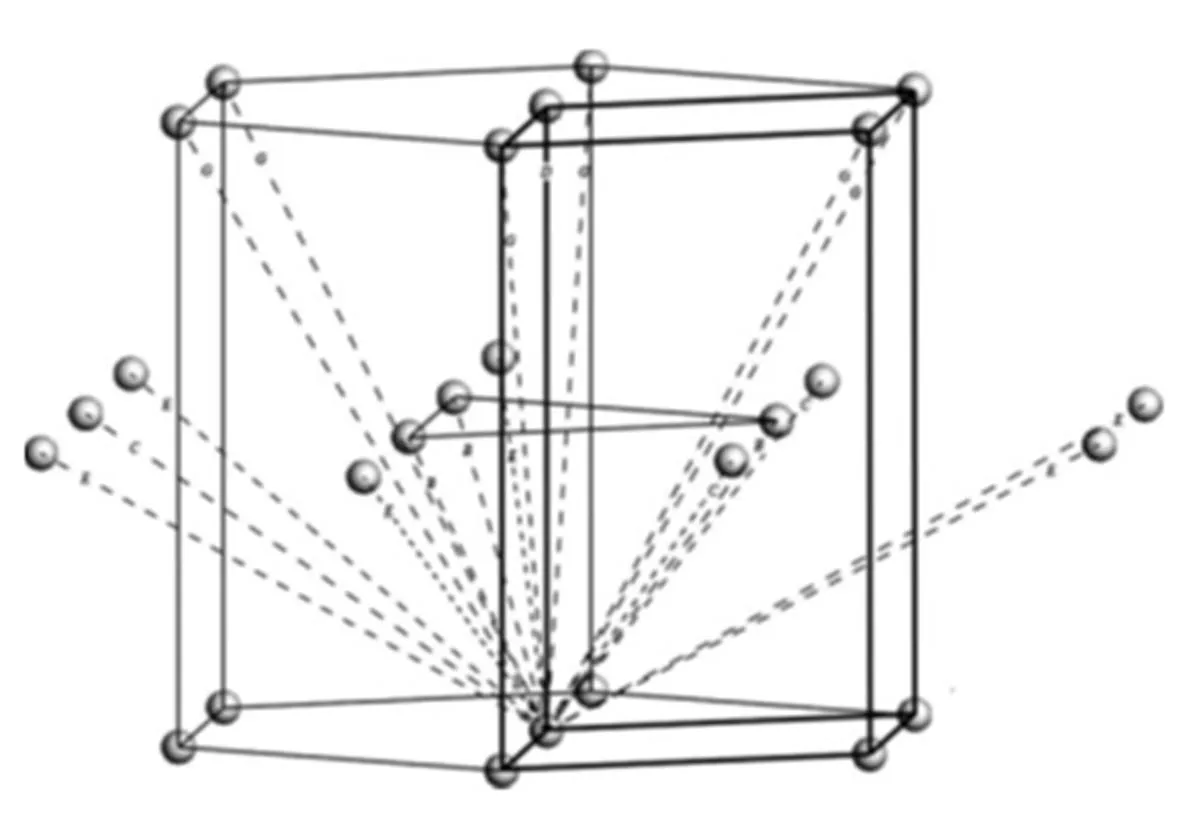
图3 密排六方金属晶面断键的空间分布

表面能的计算公式如下[18]：

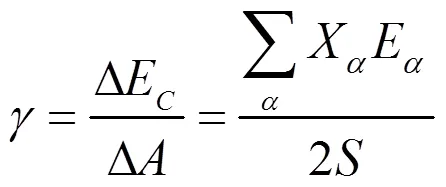
将相关参数代入公式（11），可以计算出Mg (0001) 晶面的表面能为349.486 KJ/mol。

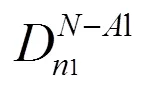
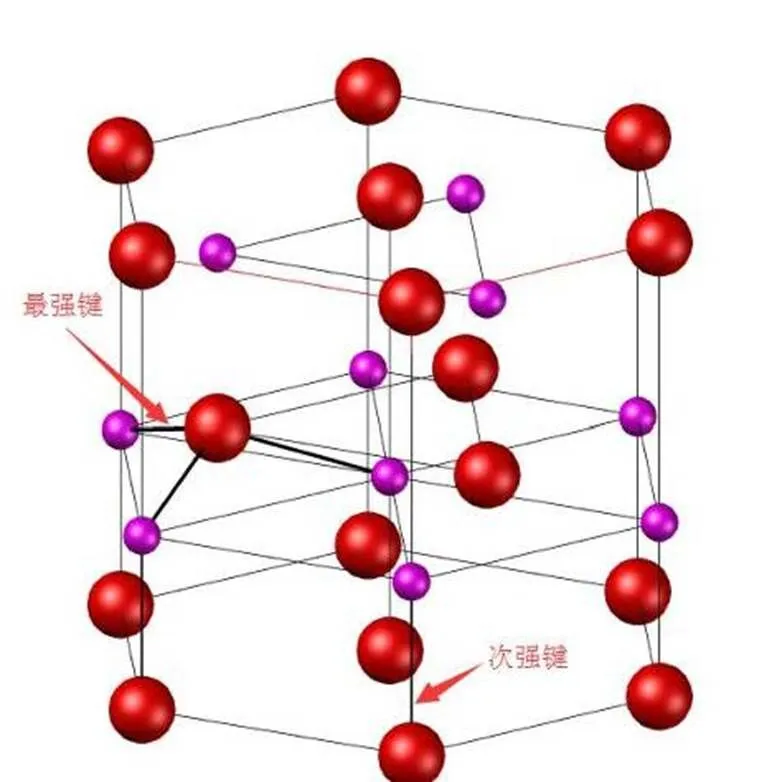
图4 AlN的键落结构示意图

2 AlN对Mg-Al合金晶粒细化机理的解释

目前，虽然有些试验结果证明AlN对α-Mg具有异质形核作用[3]，但文献[19]在使用AlN颗粒作为变质剂对Mg-Al熔体进行孕育处理的结果中指出，只有在高温条件下，AlN才会起到较好的晶粒细化作用，此试验结果也进一步说明满足晶格匹配度并非是发生异质形核的必要条件，即仅在晶体结构上满足匹配度要求的异质核心也可能不产生有效的晶粒细化效应，因此AlN的异质形核作用也有待进一步研究。从异质形核的过程来说，其本质是母相原子依附于异质相的表面生长，这必然会形成两相之间的界面。当母相与异质相之间的界面能小于母相单独形核时的固液界面能时，通常认为该异质相具有异质形核作用[20]。

Mg/AlN异质界面的界面能可表示为Mg与AlN晶体表面能的差值，根据前文的计算结果可知其值为602.489 KJ/mol。根据文献[21]可知，Mg均匀形核时的固液界面能为0.1eV，可转换为9.613 KJ/mol。根据计算结果，Mg/AlN界面能远大于Mg均匀形核时的固液界面能，因此，Mg-Al合金凝固过程中，液相中的Mg原子不能优先依附于AlN (0001) 晶面生长。根据以上分析可推断出，AlN不能有效细化Mg-Al合金的凝固组织，这是由Mg的 (0001) 晶面和AlN的 (0001) 晶面各自的表面能所决定的，这就从电子层次上解释了AlN在Mg-Al凝固过程中的微观机制。

3 结论

本文基于固体与分子经验电子理论，利用自洽键距差法计算了Mg、AlN的价电子结构、结合能以及Mg/AlN异质界面的界面能，并在电子层次上分析了AlN对Mg-Al合金凝固过程的影响机制，得到结论如下：

（1）利用自洽键距差法计算出的Mg晶体的结合能为241.2141 KJ/mol，根据断键法计算其 (0001) 晶面上的表面能为349.486 KJ/mol；

（2）利用自洽键距差法计算出的AlN晶体的结合能为337.13 KJ/mol，根据断键法计算其(0001)晶面上的表面能为951.975 KJ/mol；

（3）Mg的 (0001) 晶面和AlN的 (0001) 晶面之间的界面能为602.489 KJ/mol，远大于α-Mg形核时与液态Mg之间的界面能，导致熔体中的Mg原子不易在AlN的 (0001) 晶面上生长，解释了某些情况下AlN对Mg-Al合金的细晶效果不明显现象。

[1] QIAN X Y, ZENG Y, JIANG B, et al. Grain refinement mechanism and improved mechanical properties in Mg-Sn alloy with trace Y addition[J]. Journal of alloys and compounds, 2020, 820:1-12.

[2] JOSHI U, BABU N H. The grain refinement potency of bismuth in magnesium[J]. Journal of alloys and compounds, 2017, 695 (97): 1-5.

[3] 张玲,李英龙.镁合金晶粒细化方法研究进展[J].铸造,2019,68(11):1195-1203.

[4] HAN M, ZHU X, GAO T, et al. Revealing the roles of Al4C3 and Al8Mn5 during α-Mg nucleation in Mg-Al based alloys[J]. Journal of alloys and compounds, 2017, 705:14-21.

[5] ZHANG M X, KELLY P M, QIAN M, et al. Crystallography of grain refinement in Mg-Al based alloys[J]. Acta materialia, 2005, 53(11): 3261-3272.

[6] FAN Z, WANG Y, ZHANG Y, et al. Grain refining mechanism in the Al/Al-Ti-B system[J]. Acta materialia, 2015, 84: 292-304.

[7] KIM Y M, YIM C D, YOU B S. Grain refining mechanism in Mg-Al base alloys with carbon addition[J]. Scripta materialia, 2007, 57:691-694.

[8] 王飞.镁铝合金异质形核界面结构与特征的理论计算和实验研究[D].南昌:南昌大学,2014.

[9] 王毅,李东红,李有勇,等.压力下氮化铝相转变及结构性质的第一性原理研究[J].原子与分子物理学报,2018,35(2):277-280.

[10] 张瑞林. 固体与分子经验电子理论[M].长春:科学技术出版社,1993:1-190.

[11] LIN C, ZHAO Y, YIN G. Calculation of the lattice constant of solids with the use of valence electron structure parameters[J]. Computational materials science. 2015, 97: 86-93.

[12] LIN C, YIN G, ZHAO Y. Calculation of the cohesive energy of solids with the use of valence electron structure parameters[J]. Computational materials science, 2015, 101:168-174.

[13] LIN C, LIU Z. Statistical values of valence electron structure parameters applied to research on phase transition temperature and eutectoid reaction of titanium alloy[J]. Science in China series E: technological sciences, 2008, 51(11): 1867-1880.

[14] LIN C, LIU Z, ZHAO Y. Theoretical research on phase transformations in metastable beta-titanium alloys[J]. Metallurgical and materials transactions A, 2009, 40A(5): 1049-1058.

[15] LIN C, YIN G, LIU Z, et al. Analysis of the effect of alloy elements on martensitic transformation in titanium alloy with the use of valence electron structure parameters[J]. Materials chemistry and physics, 2011, 125:411-417.

[16] 熊欣,宋常立,仲玉林.表面物理[M].沈阳:辽宁科学技术出版社,1995:382-385.

[17] FU B, LIU W, LI Z. Calculation of the surface energy of fcc-metals with the empirical electron surface model[J]. Applied surface science, 2010, 256: 6899-6907.

[18] 付宝勤.基于固体与分子经验电子理论的表面能分析及计算[D].北京:北京化工大学，2010.

[19] FU H M, ZHANG M X, QIU D, et al. Grain refinement by AlN particles in Mg-Al based alloys[J]. Journal of alloys and compounds, 2009, 478(1-2):809-812.

[20] FAN Z Y. An epitaxial model for heterogeneous nucleation on potent substrates[J]. Metallurgical and materials transactions A, 2013, 44(3):1409-1418.

[21] LI K, SUN Z G, WANG F, et al. First-principles calculations on Mg/Al4C3 interfaces[J]. Applied surface science, 2013, 270: 584-589.

Valence Electron Theoretical Study on the Effect Mechanism of AlN on the Solidification Process of Mg-Al Alloy

ZHANG Ai-min1,2, WEI Jia-hong3, MA Bing-xin1, ZHANG Qian1, TAO Kai1,2, JI Sheng-ya1,2

(1. School of material science and engineering, Henan Institute of technology, Xinxiang 453003, China；2.Engineering Technology Research Center for metal material modification technology of Henan province, Xinxiang 453003, China; 3. School of Electrical Engineering and Automation, Henan Institute of technology, Xinxiang 453003, China)

This paper using the empirical electron theory of solids and molecules (EET)investigated the effective mechanism of Mg-Al alloy treated by AlN, builded the calculation model of the crystal structure of Mg and AlN, calculated the valence electron structure and binding energy of Mg and AlN crystal by the self-consistent bond length difference method (SCBLD). Using dangling bond analysis method calculated the surface energy of Mg and AlN terminated with (0001) crystal face, further the interfacial energy between Mg/AlN heterogeneous interface had been obtained. The results indicate that interface energy of Mg/AlN is larger than that of solid/liquid when Mg nucleates homogeneously, therefore, Mg atom in melt cannot stack and grow on the (0001) face of AlN, the refining effect of AlN on Mg-Al alloy is not obvious, which further explains the microscopic mechanism of AlN in the solidification process for Mg-Al alloys from electronic level.

AlN; empirical electron theory of solids and molecules; self-consistent bond length difference; valence electron structure; binding energy

TB31

A

2096–7772(2020)02–0021–09

2019-12-23

河南省科技攻关项目（192102210164）；河南工学院博士科研启动基金（KQ1848）

张爱民（1983―），男，辽宁黑山人，讲师，博士，主要从事金属材料的凝固组织控制研究。

（责任编辑吕春红）