注重互联网元素融入，培养逻辑推理素养

齐国庚

[摘   要]科技的高速发展，让“互联网+”教育成为必然。如何在数学教学中融入互联网元素，培养学生的数学核心素养是当代数学教师亟待解决的一个问题。文章从教学软件、教学平台、趣味网站在数学教学中的应用出发，谈谈在数学教学中，融入互联网元素，创设灵动开放的数学活动，以培养学生逻辑推理素养的一些尝试。

[关键词]互联网;核心素养;逻辑推理;知行合一;析理以辞;寓学于乐

[中图分类号]   G633.6       [文献标识码]   A        [文章编号]   1674-6058（2020）15-0058-03

义务教育数学课程标准指出：“推理能力的发展应贯穿在整个数学学习过程中，推理是数学的基本思维方式。”逻辑推理是中学数学核心素养之一。逻辑推理是得到数学结论、构建数学知识框架的重要方式。课标明确要求：“数学课程的设计与实施应根据实际情况合理地运用现代信息技术。要开发并向学生提供丰富的学习资源，把现代信息技术作为学生学习数学的有力工具。”而科技的高速发展，让具有信息化、个性化、交互性、拓展性、共享性诸多特点的“互联网+”教育优势突显。因此，当代教师应研究如何与时俱进，将互联网元素融入数学教学中，构建一种新型的学生数学学习舞台，以更具前瞻性、科学性和操作性的方式培养学生的逻辑推理素养。本文结合案例，谈谈笔者所做的一些尝试。

一、知行合一——教学软件融入教学，培养学生的逻辑推理素养

明朝思想家王阳明的“行是知之始，知是行之成。”提倡的传统思想是“知行知”，即知识是行动的基础，行动成全了知识。学生在课堂上获取知识后，课后更需要有充分的时间和空间去内化知识，形成和发展逻辑推理素养，逻辑推理本质上是靠学生“悟”出來的，而不是老师教出来的。而现今许多学科软件，为我们提供了让学生能够知行合一的辅助手段。以下就是利用story line软件设计的一份课外作业：这个课件由两个微课、四个层层递进的变式作业构成，课件设计可由图示流程图说明。

【微课一】

2.例题一的解答思路分析。

3.结合例题讲解，归纳总结数式规律，探索解题的一般步骤。

第一步：找序数。一般用n表示数式的序号。

第二步：找规律。分别比较数式中数据与序号之间的关系，寻找式子变化规律，然后用含序数的代数式表示出来。

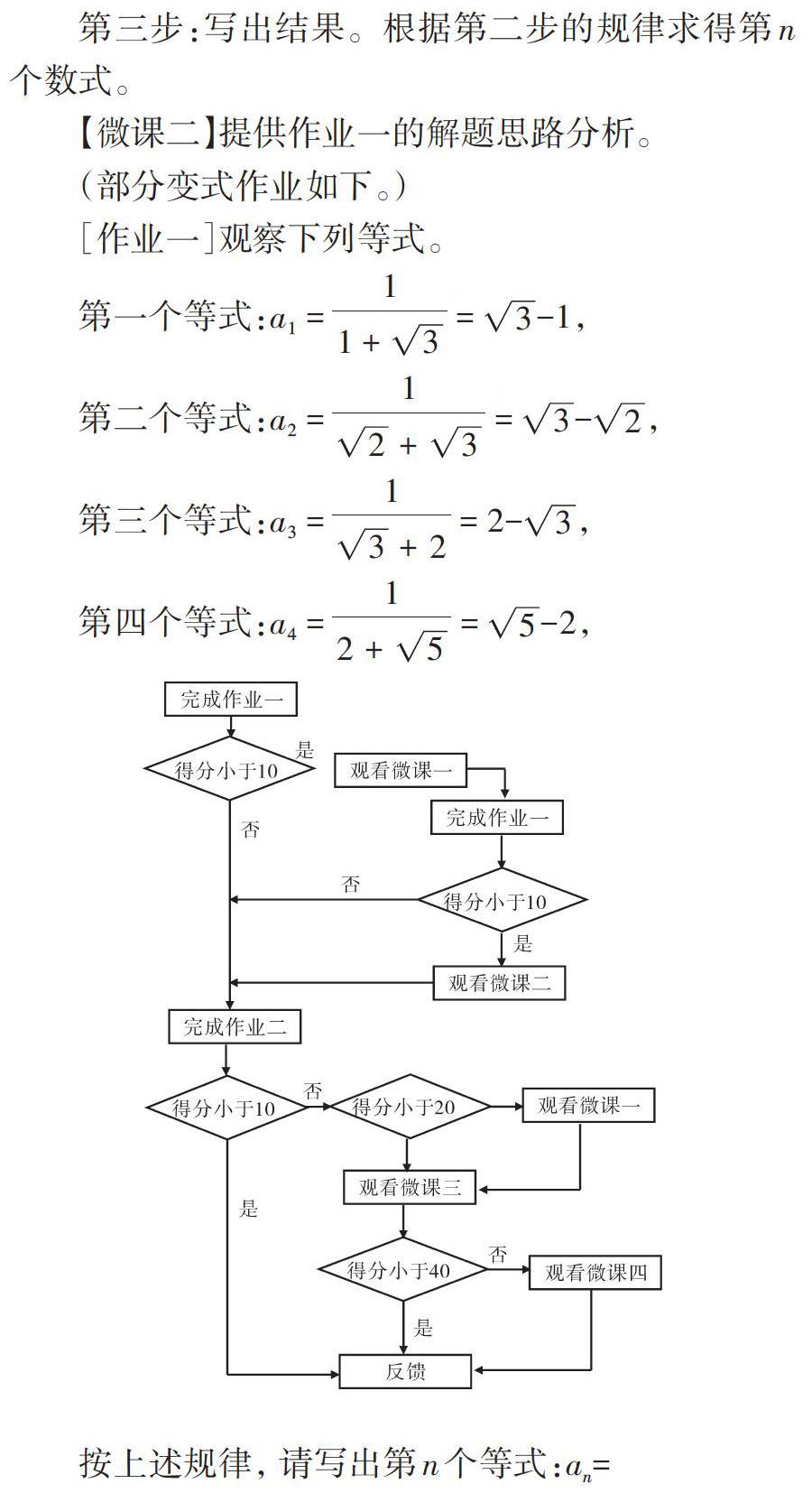
第三步：写出结果。根据第二步的规律求得第n个数式。

【微课二】提供作业一的解题思路分析。

（部分变式作业如下。）

[作业一]观察下列等式。

[作业二]如图，用两种颜色（黑色和白色）的菱形纸板，按黑色纸板数逐渐增加1的规律拼接成如下图案，若第n个图案中有2017个白色纸板，则n的值等于（） 。

A.671          B.672        C.673        D.674

这个课件的设计，就是为了让学生达到 “知行合一”：学习知识后实践，实践时发现疑难，继续学习知识，然后再实践，最后理解知识，将其内化为能力和素养。同时，课件还可以给教师提供学生的学情反馈，教师能够在学生有困难的时候予以适时的、有针对性的、个性化的干预和引导。“藏息相辅”源于中国古代《学记》，意思是教师的讲解要与个人的理解相结合才能消化知识，这正是设计这个story line课件的初衷。这个课件的设计，通过微课的引导与分阶变式练习的融合，让逻辑推理与直观操作有机结合起来，让逻辑推理成为直观操作后分析问题得出结论的自然延续。这正符合义务教育数学课程标准的理念，遵循初中生的学习规律和初中生心理发展的需要，着重于直观操作，学生从掌握的知识实际出发，不断尝试，教师给学生提供“悟”的平台，以培养学生的逻辑推理素养。

二、析理以辞——教学平台融入教学，培养学生的逻辑推理素养

在逻辑推理中，推理论证能力当属最具特色又备受重视的能力之一，也是初中数学教育的重中之重。魏晋时期的大数学家刘徽提出了“析理以辞”，这里所说的“辞”，就是指逻辑与逻辑理性的推理过程及表述。那么，如何能让学生用严谨的逻辑推理来进行表述呢？反思，应该是一种很好的培养逻辑理性思维的方式，也就是教师要引导学生反思解题步骤，在反思中体会数学思想方法，归纳解题规律。那么，如何进行反思呢？《墨子·小取》中有这么一段话：“夫辩者，将以明是非之分，审治乱之纪，明同异之处，察名实之理，处利害，决嫌疑。”意思是：辩论的目的，是要分清是非的区别，审察治乱的规律，搞清同异的地方，考察名实的启发，断决利害，解决疑惑。在互联网时代，提供给我们适时的线上交流平台，如QQ、教育资源公共平台的教师空间和学生空间等等，也就提供了让学生通过 “辩”来析理以辞的平台。以下是一个利用教育资源公共平台实现全员参与辩论的案例，这个案例起源于一道学生练习。

如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm，求这个正方形的边长。

学生典型错误分析：

本题主要考查的是相似三角形的判定、性质和矩形的判定、性质，重点考查对应线段（高）的比等于相似比。所以，解此题要先证明四边形EFDM是矩形，通过设正方形边长为x，利用△AEH∽△ABC，得[EHBC=AMAD]，求正方形边长。主要问题在于：（1）学生推理不够严谨，在表示DM长度时未证明四边形EFDM是矩形，直接得出DM=x;（2）由EH∥BC，得出[EHBC=AMAD]，忽视对应线段（高）的比等于相似比的前提条件“对应高”的说理，没有证明AM⊥EH，暴露出学生对定理条件理解不透;（3）在证明AM⊥EH时，直接由EH∥BC，AD⊥BC，得出AM⊥EH，学生忘记结论不能作为证明的理论依据，要通过平行线的性质定理证明垂直。

如何让学生发现错误，纠正错误，并准确表述证明过程呢？教师可以收集学生的典型错例，发布在教育资源公开的教师空间，然后分阶段给学生发布学习任务。首先，让学生到空间去纠错订正，征求其他解法，要求将成果发布于学生空间，然后让学生去同学的空间对成果进行评价。这样的数学活动设计，给学生提供了辨析的空间，更关键的是为教师提供交流的平台，剖析学生的思维过程，教师可以实时提出合适的问题，启发学生思考或者与同学交流讨论，让其掌握知识技能的同时，感悟數学思想，积累数学思维的经验，提升数学核心素养。

三、寓学于乐——趣味网站设计融入教学，培养学生的逻辑推理素养

《学记》中的“大学之教也，时教必有正业，退息必有居学”，就是主张学习应该课内与课外相结合。数学推理能力的培养不仅限于课堂，课外活动或游戏也是培养学生逻辑推理能力的有效途径。教师利用熟悉的素材设计富有趣味性的活动（折叠矩形纸片、摆放一副三角尺）、推荐趣味益智网站等，能让学生在“玩”中提高逻辑推理能力。

[作业一]将下面的卡片折成正方体，可以形成哪个选项的图形？

[作业二]下面卡片能折成正方体的是（）

A. ①②                       B. ①②③

C. ①②③④⑥           D. ①②③④⑤⑥

作业一是一道门萨智商测试题，作业二是初一数学习题，两者极其相似，考查的都是学生的逻辑推理能力。门萨测试是全球规模最大且历史最久的智商测试，由门萨国际（Mensa International）在世界范围内组织开展，它一般从注意力、观察力、逻辑思维、想象力和记忆力这几个方面出题。类似的游戏还有许多，如数独，数独是源自18世纪瑞士的一种数学游戏，在解数独的过程中，可以有效地锻炼大脑的反应能力和逻辑推理能力。由此可见，寓学于乐，把逻辑推理问题结合到日常生活实例中，以游戏的方式呈现，通过观察、猜测、分析和解决问题等活动，感受数学思想的奇妙与作用，体会推理论证的严谨性、精确性，能更好地促进学生数学逻辑推理素养的提升，使其学会欣赏数学智慧之美。

综上，为了培养学生的逻辑推理素养，教师在教学过程中，应该根据教材和学情，有机地融入互联网元素，提高课堂教学的趣味性，培养学生积极的推理意识，锻炼学生的创造性思维，提升学生的逻辑推理素养。

[   参   考   文   献   ]

[1]  史宁中.试论数学推理过程的逻辑性——兼论什么是有逻辑的推理[J].数学教育学报，2016（8）：1-16 .

[2]  陈诚.数学核心素养之逻辑推理能力提升的研究[J].数学之友，2016（16）：14-16.

[3]  洪燕君，周九诗，王尚志，鲍建生.普通高中数学课程标准（修订稿）的意见征询——访谈张奠宙先生[J].数学教育学报，2015 （3）：35-39.

（责任编辑    黄诺依）