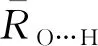OH-(H2O)n (n=1～8)团簇的量子化学研究

杨忠志， 石 华,2， 刘 翠

(1.辽宁师范大学 化学化工学院，辽宁 大连 116029； 2.大连海洋大学 海洋科技与环境学院，辽宁 大连 116023)

作为水的基本组成离子，氢氧根离子在自然界中无处不在.氢氧根离子水团簇广泛分布于大气的平流层、对流层和电离层[1]，并参与许多复杂的大气物理过程[2].它们还广泛地分布在生物体中，参与很多生物化学过程，尤其是某些酶催化过程[3].此外，氢氧根离子在水溶液中的迁移率极高[4]，它们是酸碱化学反应的重要参与者.但在实验室中，很难产生可进行直接观测的基本电荷的离子水团簇.人们还未完全了解这些带有基本电荷的水团簇，尤其是对于氢氧化物水团簇[5].因此，对于氢氧根离子水团簇的结构和性质的理论研究必不可少.

人们采用各种量子化学计算方法[6-10]，讨论了小的氢氧根离子水团簇的结构、能量、光谱、多体效应、结合能、焓和质子转移等性质.实验测量以及量子化学计算结果表明，OH-的氧原子可以被2个、3个、4个或者5个邻近的水分子所包围[6,10]，呈现高配位的状态.Cappa等人[11]对OH-(H2O)进行了Mulliken 电荷布局分析，发现OH-上的13% 的电荷被重新分布到水分子上.Lee等人[12]采用NBO 电荷分析研究OH-(H2O)1～6，得到了相似的结论.此外，人们也进行了大量的从头算分子动力学(AIMD)模拟，以探讨水溶液或大的氢氧根离子水团簇的结构、光谱、扩散系数、质子转移、氢氧化物迁移和浓度分布等[6,13].

采用3种不同水平的量子化学计算方法，对OH-(H2O)n(n= 1～8)团簇进行结构、二阶稳定化能、结合能等性质的研究，并讨论其稳定构象的电荷分布及电荷转移性质.

1 计算方法

采用Gaussian 09量子化学计算软件，分别在B3LYP/6-31++G(d,p)、MP2/6-31++G(d,p)、MP2/aug-cc-pVDZ水平下，对OH-(H2O)n(n= 1～8)团簇进行结构优化，同时进行频率计算，以保证优化得到的构象是稳定的.

量化计算采用较高的基组可以给出更加准确的能量和几何构型，但对于局域电荷的计算，采用低基组会比高基组更适合.这是因为弥散基组可能在某种程度上越过自身原子的区域，到达相邻的其他原子的区域，这样会导致Mulliken电荷的结果被过高地估计[14].Derouane和他的合作者[15]建议计算电荷采用STO-3G基组更为可靠.Wilson和 Ichikawa[16]以及Torrent-Sucarrat等人[17]指出，如果采用极化基组，电荷转移的结果会被过高估计.根据本课题组以及其他人的经验，在HF/STO-3G水平下，分析了上述稳定构象下的OH-(H2O)n(n= 1～8)团簇的电荷分布和电荷转移.

二阶稳定化能-ΔE(2)能够描述氢键的强弱，采用式(1)进行计算[18]:

(1)

其中，qi是电子轨道的占据数，Fij是Fock矩阵的矩阵元，Ej-Ei是供体轨道和受体轨道的能级差.分别对上述稳定构象的OH-(H2O)n(n= 1～8)团簇进行NBO分析，计算氢氧根离子与第一壳层水分子形成的二阶稳定化能.

采用式(2)，分别用上述3种量子化学计算方法，计算OH-(H2O)n(n= 1～8)团簇的结合能：

ΔEn=E[OH-(H2O)n]-E[OH-]-nE[H2O].

(2)

计算进行了零点能校正(ZPE)以及基组重叠误差校正(CP)，其中,B3LYP/6-31++G(d,p)的零点能校正因子为0.94[19]，MP2/6-31++G(d,p) 的零点能校正因子为0.96[19]，MP2/aug-cc-pVDZ的零点能校正因子为0.967 5[20].

2 结果与讨论

2.1 OH-(H2O)n (n = 1～8)团簇的几何结构

对于OH-(H2O)n(n=1～8)团簇,分别采用B3LYP/6-31++G(d,p)、MP2/6-31++G(d,p)、MP2/aug-cc-pVDZ方法优化几何结构，并进行频率计算，均优化得到21个稳定构象，且3种方法得到的多数构象是非常接近的.将MP2/aug-cc-pVDZ水平下优化得到的21个稳定构象列于图1中.除B3LYP/6-31++G(d,p)水平下优化得到的6-a构象，第一壳层水分子的数目为4个，而MP2/6-31++G(d,p)及MP2/aug-cc-pVDZ水平下优化得到的构象第一壳层水分子为5个，其他20个构象都比较接近.使用l-k(m+n)符号对构象进行标记.其中,l表示团簇中水分子的总数目，k是在l相同时构象的序列号，m是第一壳层水分子的数目，n是外壳层水分子的数目.

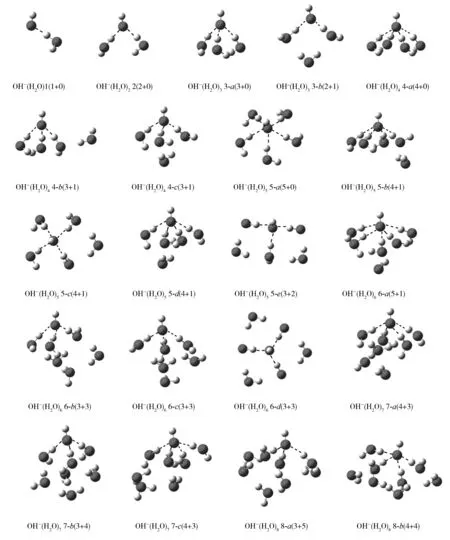
图1 MP2/aug-cc-pVDZ水平下优化得到OH-(H2O)n (n=1～8)团簇的稳定构象

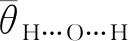
表1 3种量化方法优化得到的几何结构

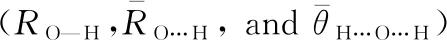
Table 1 Optimized structures obtained from three methods of

注：方法1,B3LYP/6-31++G(d,p);方法2,MP2/6-31++G(d,p);方法3,MP2/aug-cc-pVDZ

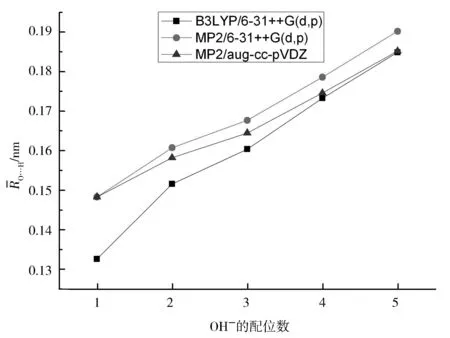
图2 平均氢键长随配位数的变化趋势

2.2 OH-(H2O)n (n=1～8)团簇的电荷分布及电荷转移

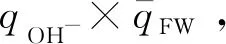
表2 3种量化方法的与|ΔqOH-|结果

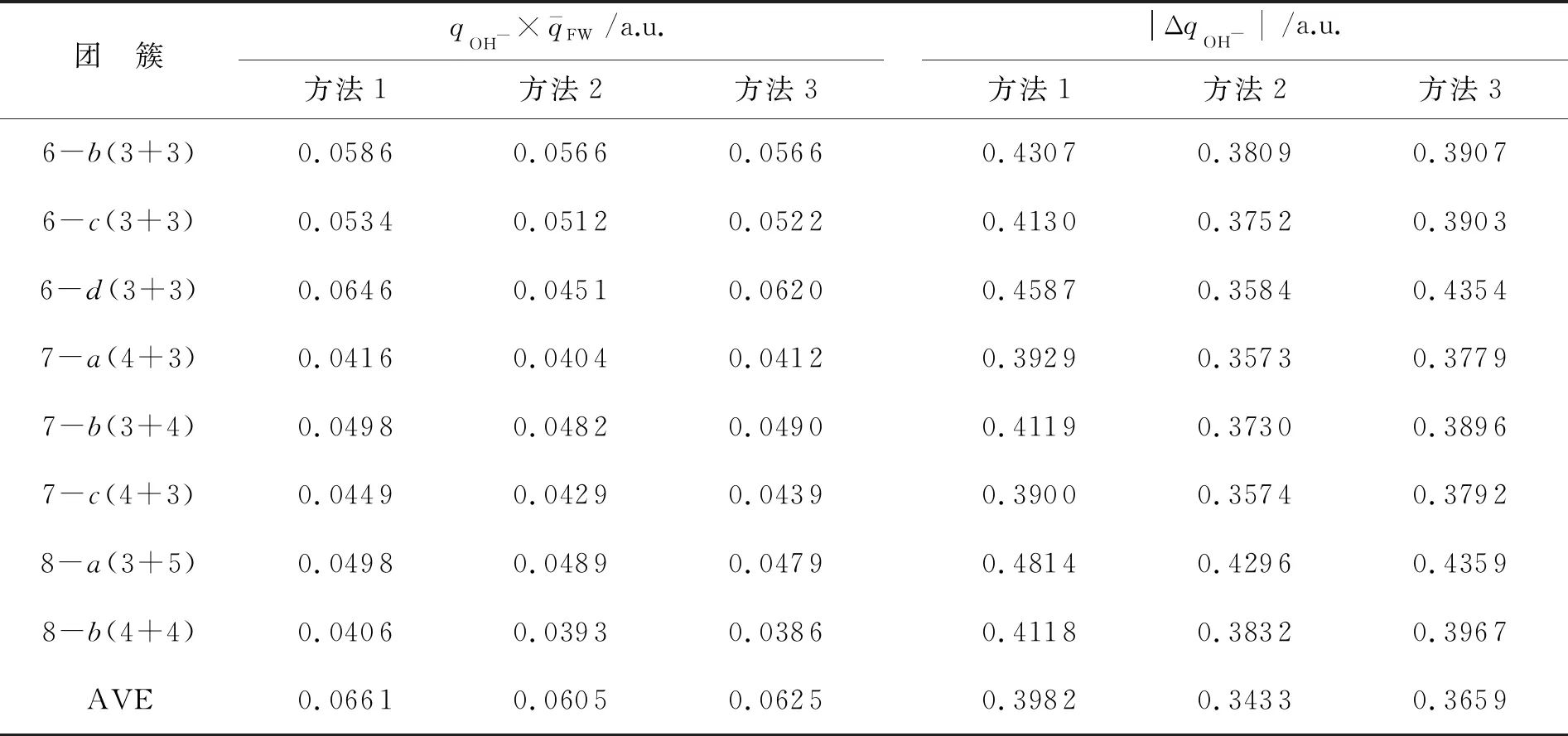
表2(续)

注：AVE表示平均值；方法1，B3LYP/6-31++G(d,p)；方法2，MP2/6-31++G(d,p)；方法3，MP2/aug-cc-pVDZ

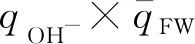
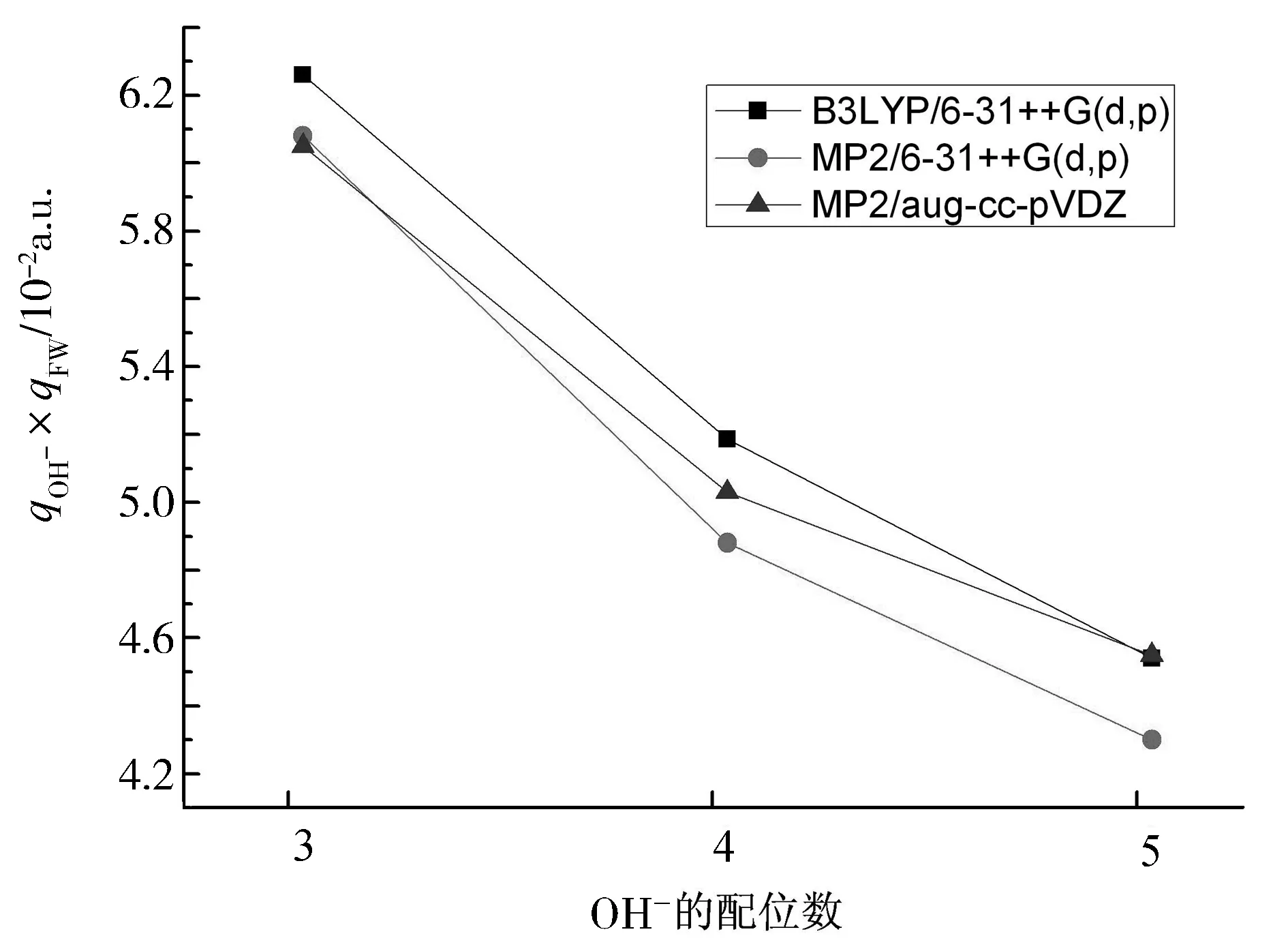
图3 OH-(H2O)5团簇的氢氧根离子的总电荷与第一壳层水分子的平均电荷的乘积随配位数的变化趋势

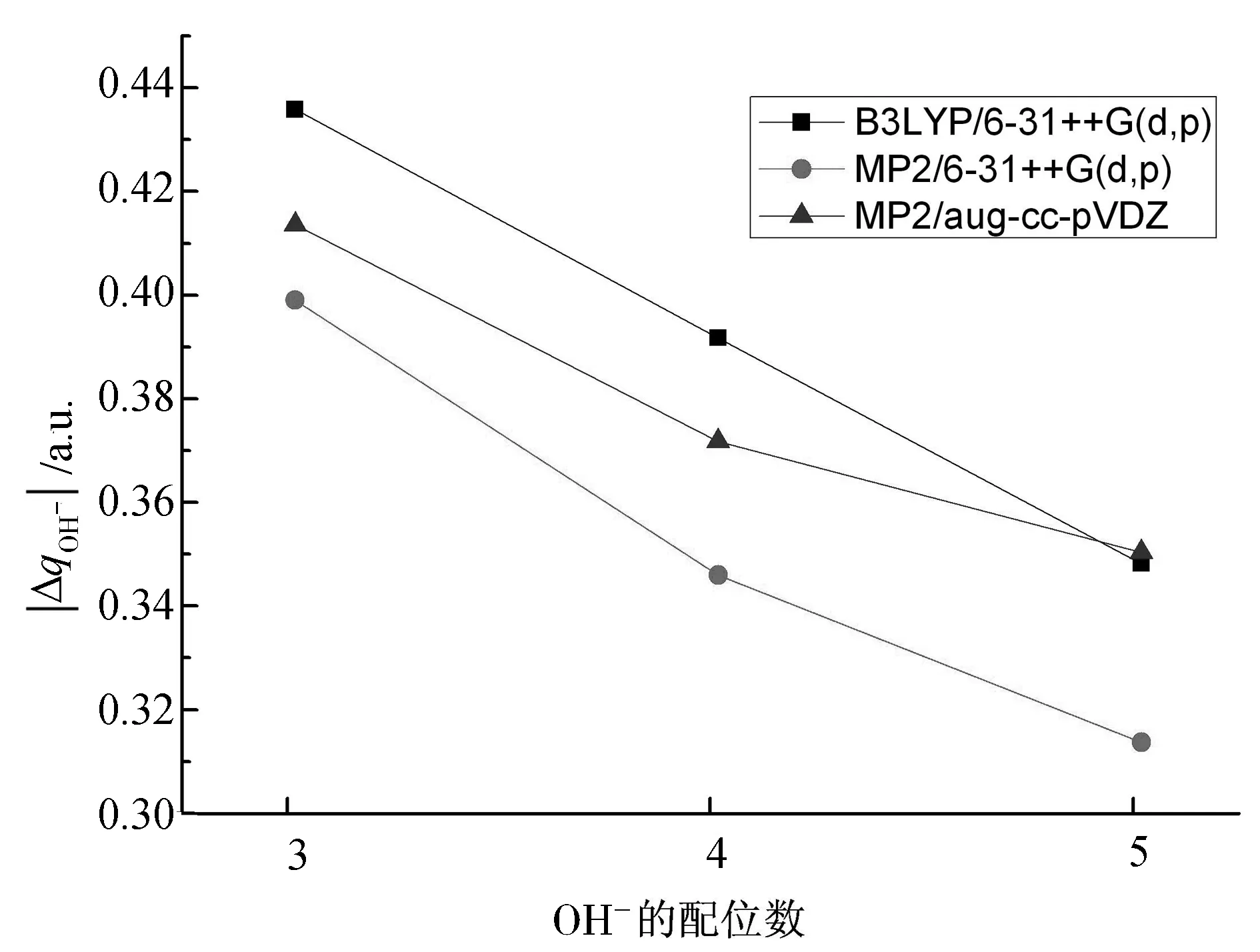
图4 OH-(H2O)5团簇的氢氧根离子电荷转移量的绝对值(|ΔqOH-|)随配位数的变化趋势

2.3 OH-(H2O)n (n=1～8)团簇的二阶稳定化能

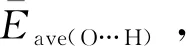
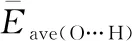
表3 平均二阶稳定化能的3种量化方法计算结果

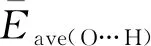
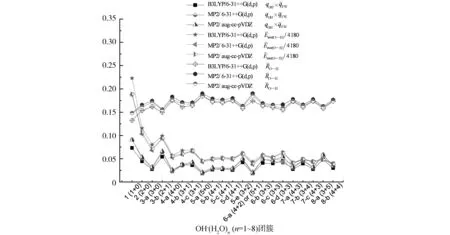
图5 OH-(H2O)n (n =1～8)团簇的氢氧根离子总电荷与第一壳层水分子的平均电荷的乘积平均氢键长平均二阶稳定化能的变化趋势

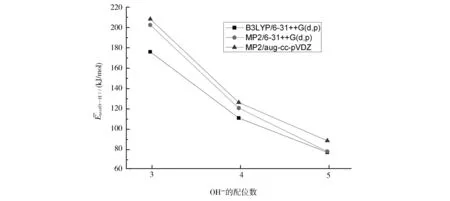
图6 OH-(H2O)5团簇的平均二阶稳定化能随氢氧根离子配位数的变化趋势

2.4 OH-(H2O)n (n= 1～8)团簇的结合能

3种水平下计算得到的团簇的结合能列于表4中.其中,B3LYP/6-31++G(d,p)水平下得到的结合能绝对值最大，MP2/aug-cc-pVDZ水平下得到的结合能绝对值最小.

3种量化计算结果表明，水分子数目相同的氢氧根离子水团簇，结合能结果比较接近.但结合能的大小排序，3种量化计算的结果并不一致.

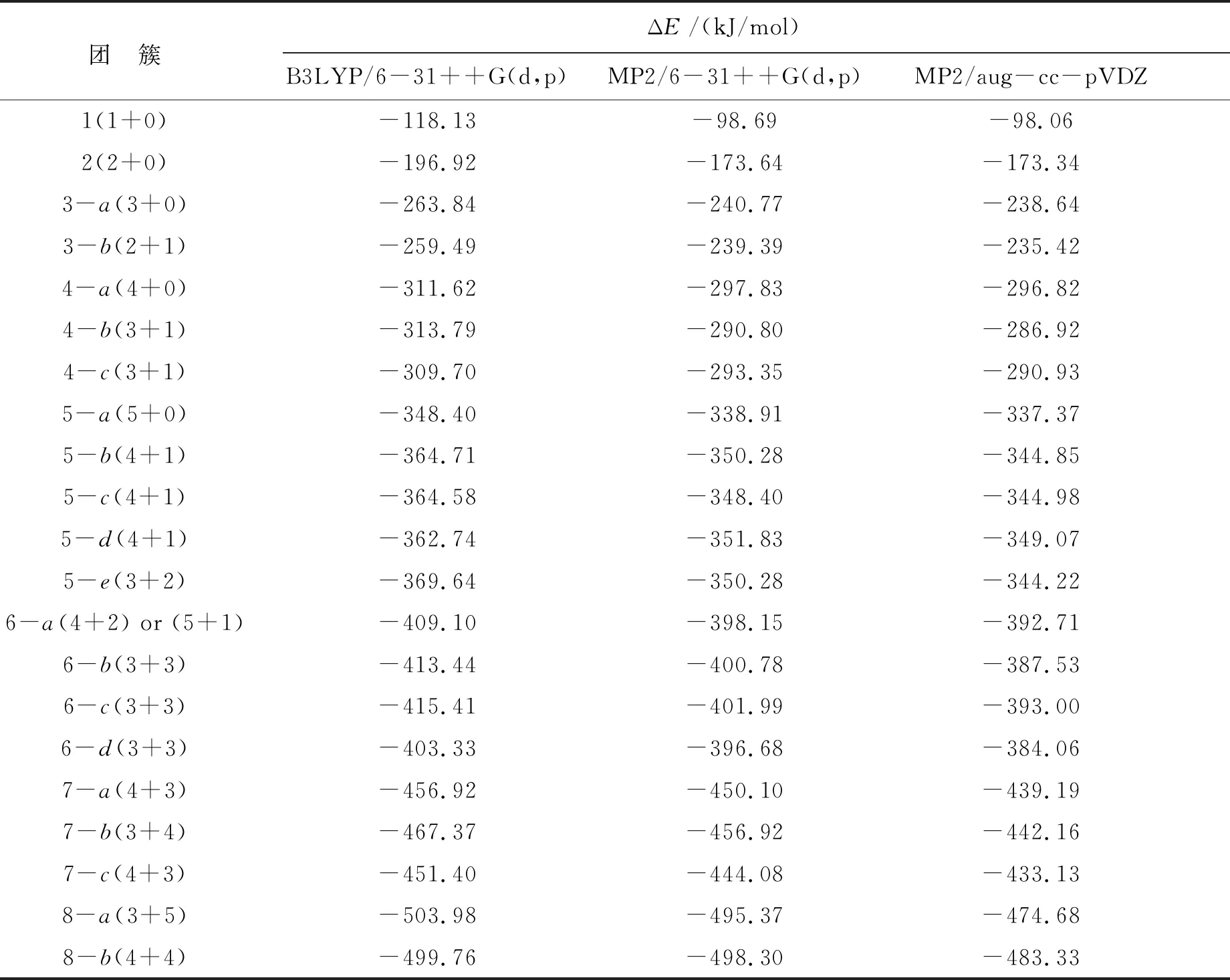
表4 OH-(H2O)n (n=1～8)团簇结合能的3种量化方法计算结果

将水分子数目相同的氢氧根离子水团簇的结合能进行统计平均，得到图7.图7表明，随着水分子数目增多，氢氧根离子水团簇的结合能绝对值增大，而且3条曲线趋势完全一致，说明3种方法得到的结论是一致的.

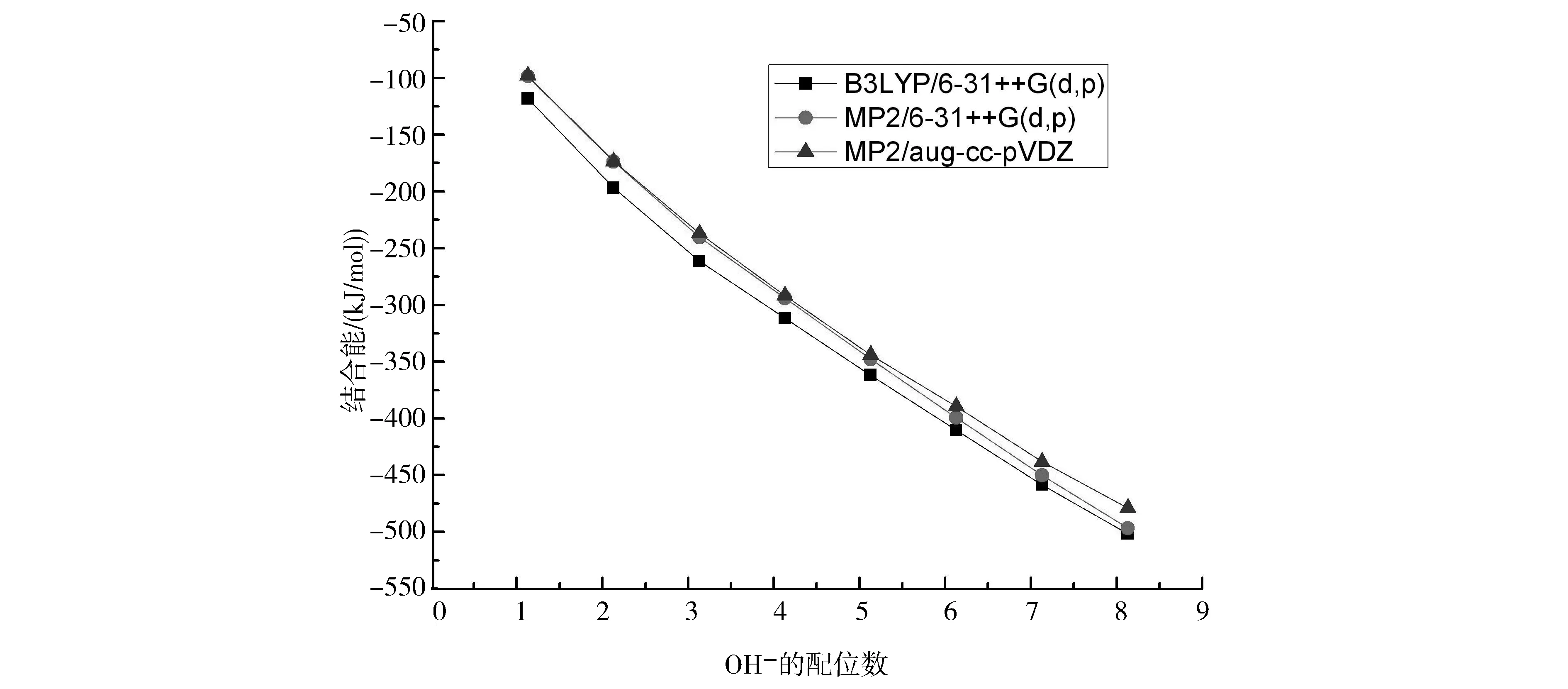
图7 OH-(H2O)n (n=1～8)团簇结合能随水分子个数变化趋势

3 结 论