平环图着色的性质

韩友发, 王 雪, 李丹丹

(辽宁师范大学 数学学院，辽宁 大连 116029)

纽结理论是20世纪以来作为拓扑学的一个重要部分而发展起来的，其核心工作之一就是研究纽结在连续变形下保持不变的特性.由于纽结与链环既直观又奥妙，纽结理论成为拓扑学中引人入胜的一个分支，被广大的专家学者所重视，这些专家一直在寻找鉴别力强的纽结不变量.1928年，Alexander取得了重大突破，他将每个纽结联系上一个多项式不变量，称为Alexander多项式[1-2]. 1969年，Conway[3]研究了Alexander多项式的性质时，发现了一个计算公式，进而给出了Alexander多项式的递推公式，但是这个多项式不能区分镜面像.1984年，Jones[4]在研究泛函算子代数时给出了一个新的纽结不变量，后来称为琼斯多项式，它可以区别某型纽结及其镜面像.到了1988年，Kauffman[5]一般化了Jones多项式，这些思想和方法在纽结理论的研究中发挥重要作用.同时，很多专家学者发现了纽结理论与图论有着很多内在的联系，即纽结的平面投影图与它的平面图是建立了一一对应的.由于这些发现极大促进了纽结理论自身发展，为纽结理论在图论的应用提供有效的思想和方法.

1 预备知识

1.1 图的相关定义

定义1.1一个图是一个序偶〈V,E〉，记为G=(V,E),其中：

(1)V是一个有限的非空集合，称为顶点集合，其元素称为顶点或点.用V(G)表示顶点集合；

(2)E是由V中的点组成的无序对构成的集合，称为边集，其元素称为边，且同一点对在E中可以重复出现多次.用E(G)表示边的集合.

定义1.2如果V(G′)⊆V(G),E(G′)⊆E(G)，那么称图G′为图G的子图.

定义1.3如果G中两个顶点之间有多重边或有一个顶点带一个环，那么称图G为多重图.

定义1.4图G的k-着色是k种颜色在G的面上的分配，使得相邻的两个顶点涂不同的颜色，就称面着色的图为k-可着色.使G为k-可着色的最小k称为G的着色数，记为x*(G).

定义1.5平面图H是由顶点、边和面(边围成的区域)组成的，其对偶图H*定义如下：H中每一个面f内取一点作H*的一个顶点f*，G*中的f*、g*相连接e*的充要条件是f*、g*在H中对应的面f，g含公共边e，且使e和e*相交.

注本文研究平面图H着色的性质，把H的各个区域涂上颜色，使其相邻的面(有公共边的面)有不同的颜色，从而可以转化为研究对偶图H*的着色性质.

1.2 图的多项式

首先介绍图的双色多项式Z(G)，它有两个变量q和v，满足下面3个条件：

(1)Z(•)=q;

(2)Z(•G)=qZ(G);

引理1.1[6]在图多项式Z(q,v)中，当v=-1时，图多项式特殊化为色多项式P(G).P(G)代表对图G的顶点用q种颜色涂色，使得相邻的两个顶点不同色的涂法的数目.

引理1.2[7-8]如果图G是子图G1和G2的不交并，那么P(G)=P(G1)P(G2).

引理1.3[7-8]如果图G是子图G1和G2的并，满足G1∩G2是一个顶点，那么

qP(G)=P(G1)P(G2).

1.3 广义剖分

定义1.6对于每个单纯复形K，选择其重心O，把重心O与单形的相应的顶点相连接起来的一种剖分，把这种剖分称为广义剖分.记为TkK(k≥1).

例单形K的一次广义三角剖分(图1).

图1 三角形的一次广义剖分

定义1.7设拓扑空间X为多面体，若存在单纯复形K与同胚f:|K|≅X,则把单纯复形K与同胚f这个对偶(K,f)称为拓扑空间X的一个三角剖分.

2 平环平面图的着色性质

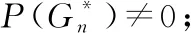
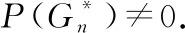
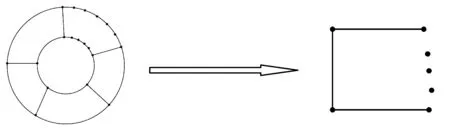
图2 带有n区域的平环Gn和它的对偶图

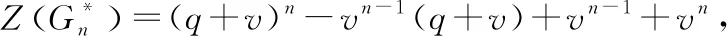
注该引理的结论从几何直观上也容易得到.主要是下面的定理证明时要用到引理证明中的思想和公式.

定理2.1设Gn是平环中含有n个区域的图，对区域图Gn进行一次广义剖分后，所得图T1Gn的着色数目与Gn的着色数目一样(图3).

证

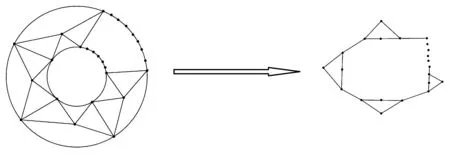
图3 Gn的广义剖分T1Gn和它的对偶图

根据双色多项式的计算法则有

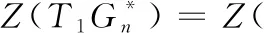
当v=-1时，

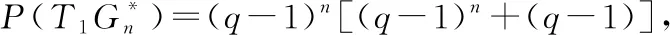
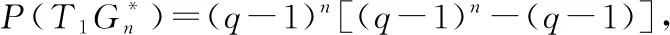
因此，对带有n区域图Gn进行一次广义三角剖分后，这个图的涂色数目与剖分前的涂色数目具有不变的性质. 从而定理得证.

定理2.2设图G是由区域图Gt和区域图Gs组成，并且它们具有一条公共边(图4)，则有

(1)当s，t中有一个为奇数时，若q≥3，则P(G*)≠0;

(2)当s，t均为偶数时，若q≥2，则P(G*)≠0.

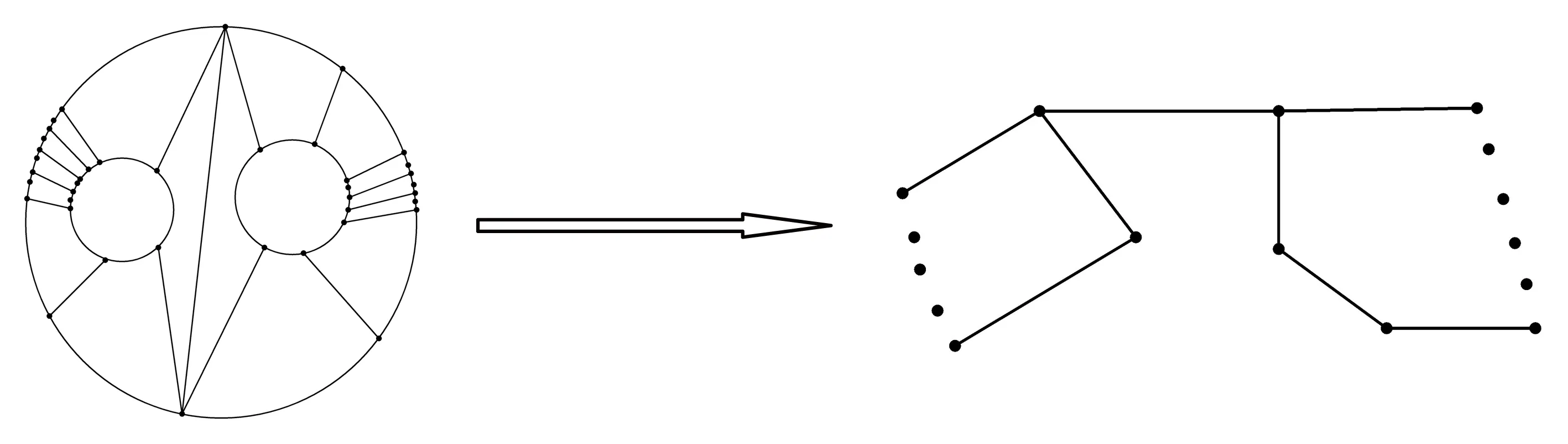
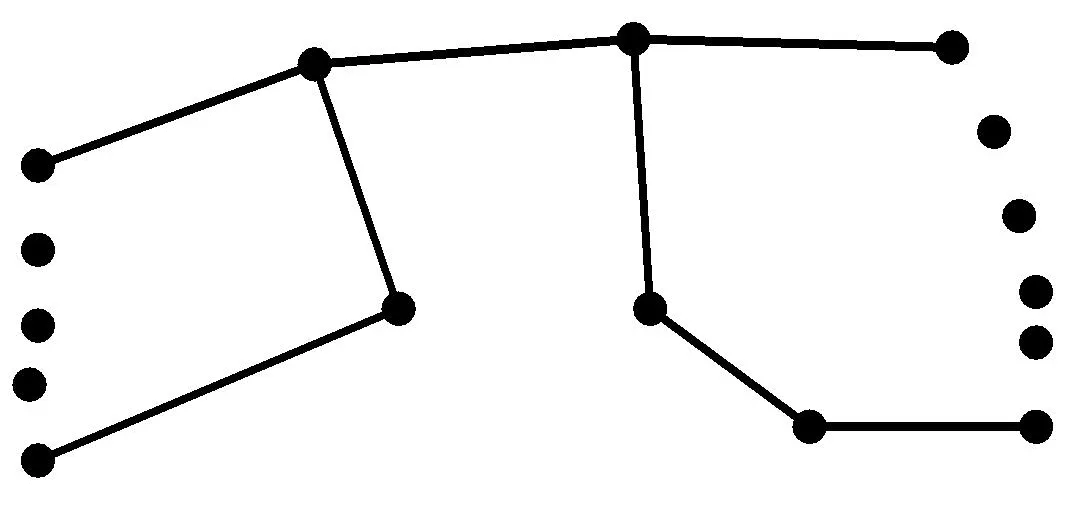
图4 两个带有一个公共边的平环区域的平面图和它的对偶图

证

由引理1.1和引理1.2可知:

当v=-1时，有

讨论情况如下：

①当t为奇数，s为偶数时，

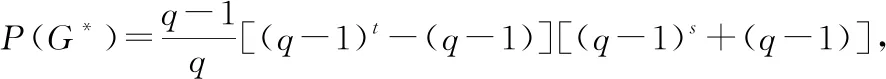
②当t为偶数，s为奇数时，

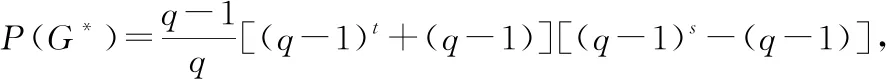
③当t，s均为奇数时，

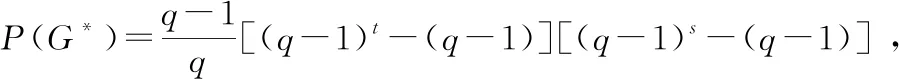
④当t，s均为偶数时，

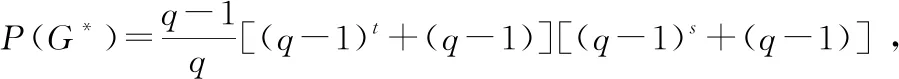
从而定理得证.

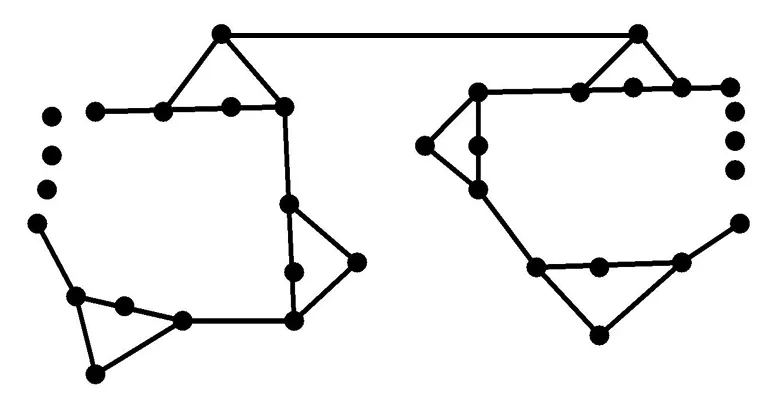
定理2.3设图G是由区域图Gt和区域图Gs组成，且具有一条公共边，对G进行一次广义剖分后，所得图为T1G(图5),则有

(1)当t，s中有一个为奇数时，若q≥3，则P(T1G*)≠0;

(2)当t，s均为偶数时，若q≥2，则P(T1G*)≠0.

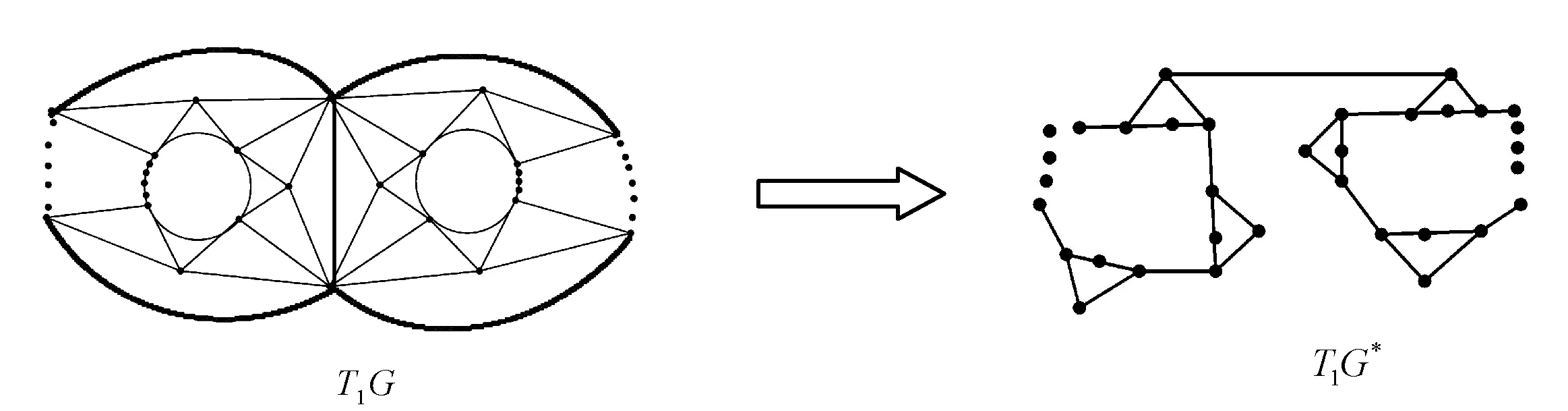
图5 平面图G的广义剖分和它的对偶图T1G

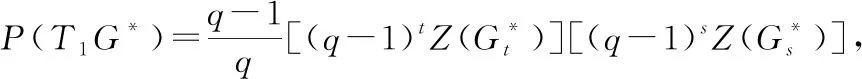
①当t为偶数，s为奇数时

当q≥3时，P(T1G*)≠0.

②同理可知，当t为奇数，s为偶数时，当q≥3时，P(T1G*)≠0.

③当t,s均为奇数时

当q≥3时，P(T1G*)≠0.

④当t,s均为偶数时

当q≥2时，P(T1G*)≠0.

从而定理得证.