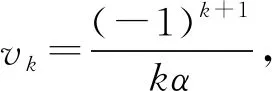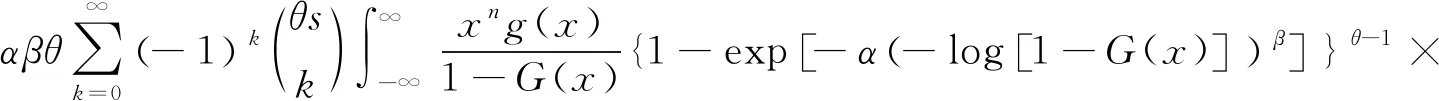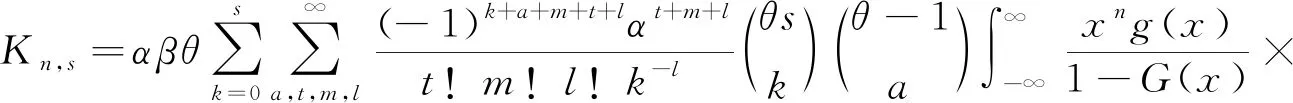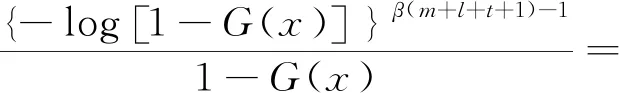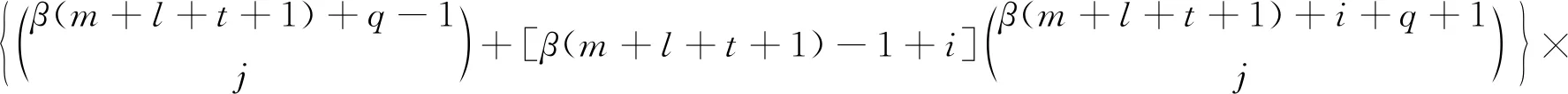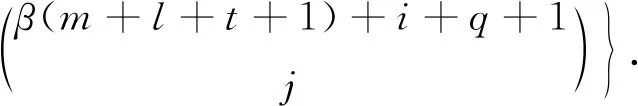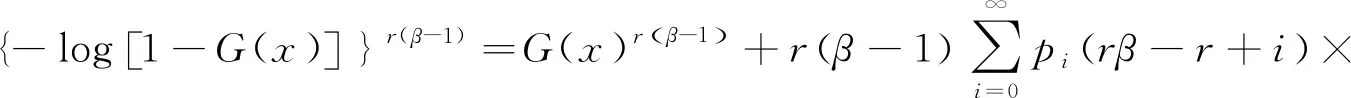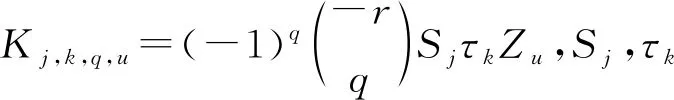基于T-X变换的广义指数威布尔分布及性质

包振华, 王海玥

(辽宁师范大学 数学学院,辽宁 大连 116029)

指数分布在可靠性领域中应用广泛，可用来描述电子产品在随机失效阶段的可靠性. 然而，由于产品自身的复杂性以及所处阶段的不确定性等因素，仅仅使用指数分布进行数据耦合是远远不够的. 基于此，文献中对指数分布进行了各种形式的推广. 例如，Barreto-Souza等[1]研究了β广义指数分布，并证明它的拟合优于Nadarajah和Kotz[2]研究的β指数分布和Gupta和Kundu[3]研究的广义指数分布.

威布尔分布是指数分布的另外一种推广形式，近年来，在工程学、生物医学、电子等领域受到了广泛的应用. 与此同时，威布尔分布所产生的局限性也逐步暴露，它难以解决失效率函数图像为浴盆或倒浴盆形状的情况. Mudholkar和Srivastava[4]提出了指数威布尔分布，该分布能很好地解决失效率函数图像为浴盆和倒浴盆形状的情形. 该分布是通过在威布尔分布中添加一个形状参数推广得到的，其分布具有单峰、浴盆和单调形状的失效率函数图像. Bourguignon等[5]研究了威布尔指数分布，实证结果显示，它比指数威布尔分布具有更优的拟合效果. Cordeiro等[6]研究了带有两个参数的广义威布尔分布族，全面地讨论了它的一般统计性质，这些模型可以应用于生存分析中的删失数据，数值分析表明该分布族具有显著的拟合优势. 其他相关模型参见文献[7].

本文使用T-X变换方法，得到一类广义指数威布尔分布，并研究了它的统计性质，包括分位数函数、概率加权矩、Rényi熵等的解析表达式.

1 模型构建

Alzaatreh等[8]提出了一种生成连续分布族的新方法，称为T-X变换法. 设随机变量X的分布函数为G(x)，概率密度函数g(x)；设T是定义在[a,b]上的连续型随机变量，密度函数为r(t)，分布函数为R(t)，则新的分布族的分布函数由下式给出:

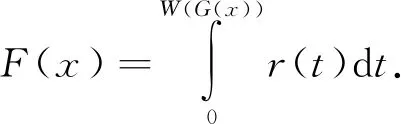
(1)

其中,W(G(x))需满足一定的附加条件，参见文献[8]. 特别的，令式(1)中W(G(x))=-log(1-G(x))，则可以得到

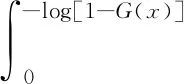
(2)

假设随机变量T具有指数威布尔分布，其分布函数定义为

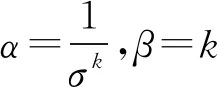
R(t)=[1-exp(-αtβ)]θ, 0≤t≤∞.

(3)

当式(2)中的T具有指数威布尔分布时，给出一个特定的分布G(x)，就可以得到一个广义指数威布尔分布，简记为GEW-G分布,分布函数为

F(x)={1-exp[-α(-log(1-G(x)))β]}θ.

(4)

式(4)对应的密度函数为

(5)

GEW-G分布允许尾部具有更大的灵活性. 当分布函数G(x)和密度函数g(x)具有简单的解析表达式,如正态分布、冈贝尔分布、对数正态分布、对数逻辑分布等，式(5)处理起来就会变得非常容易.

2 GEW-G分布函数的紧凑表达式

对于任何实参数c和z∈(0,1)，可以证明

(6)

其中,pi(c)是Stirling多项式. 前6项分别为

p0(ω)=1/2,p1(ω)=(2+3ω)/24,p2(ω)=(ω+ω2)/48,p3(ω)=(-8-10ω+15ω2+15ω3)/5 760，

p4(ω)=(-6ω-7ω2+2ω3+3ω4)/11 520,p5(ω)=(96+140ω-224ω2-315ω3+63ω5)/2 903 040.

为了分析式(4)和式(5)，对于任意的分布函数G(x)和参数a>0，定义一个新的随机变量expG(a)，其密度函数和分布函数如下:

ha(x)=aG(x)a-1g(x),Ha(x)=G(x)a.

用广义二项式定理和幂级数展开式(2)，得到

将{-log[1-G(x)]}β m用式(6)展开，得到

将G(x)β m和G(x)i+β m+1用幂级数展开，代入F(x)得到

因此，F(x)可以表示为

(7)

其中,Hk(x)表示expG(k)分布的分布函数,其中,

(8)

对式(7)求导得到相应的密度函数为

(9)

其中,hk+1(x)表示expG(k)分布的密度函数，vk=ωk+1.

3 GEW-G分布的统计性质

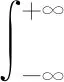
本节讨论GEW-G的相关统计性质.首先，给出GEW-G分布的分位数函数的表达式.设QG(u)=G-1(u)为G的分位数函数，其中,0

(10)

式(10)表明GEW-G的分位数函数可以用G的分位数函数来表示. 特别的，当u=1/2时，GEW-G的中位数可以表示为

还可以使用式(10)通过将u设置为单位区间(0,1)中的均匀随机变量模拟GEW-G随机变量. 将式(10)用幂级数展开，可以得到:

假设随机变量Y服从GEW-G分布,Y的(n,s)-阶概率加权矩定义为Kn,s=E[YnF(Y)s]，利用二项式定理可以得到

将Kn,s中的指数用幂级数展开并整理得

用式(6)，经计算可得

用广义二项式定理展开G(x)β(m+l+t+1)+q-1和G(x)β(m+l+t+1)+i+q+1，可以得到

令

则有

(11)

其中,

式(11)可应用于多数基准G分布.

最后讨论GEW-G分布的熵. 熵是随机变量不确定性的一种度量. 一种常用的熵测度是Rényi[9]提出的. 密度函数为f(·)的随机变量的Rényi熵定义如下:

当随机变量Y服从GEW-G分布时，

{exp[-α(-log(1-G(x)))β]}r(-log(1-G(x)))r(θ-1).

将上式用广义二项式定理展开

{αr(θ-1)[-log(1-G(x))]β}m=

(12)

其中,

(13)

(14)

用式(6)和二项式定理得

其中,

所以,

则Y的Rényi熵为