基于CVaR投资组合优化的迫近束方法子问题及其对偶

沈 洁， 赵予嘉， 姜兴睿， 王朗迪

(辽宁师范大学 数学学院，辽宁 大连 116029)

在投资过程中,希望收益越大越好,相应风险越小越好.在该条件下，Krokhmal[1]证明了以下3种风险投资中的经典模型,即风险极小化模型、期望收益极大化模型、风险厌恶模型是等价的,故可以选择其中一种展开研究.束方法是目前公认的求解非光滑优化最有前景的算法之一,可分为迫近束方法、信赖域束方法、水平束方法等[2].对于约束优化问题,可通过引进改进函数[3]将其转化为无约束优化问题,使复杂问题简单化,便于求解.本文基于CVaR最小化的投资组合问题,采用束方法对其进行研究,从对偶角度进行分析,得到其子问题解的表示式,同时得到其中一些相关重要关系.

1 预备知识及模型简介

首先给出与束方法相关的一些预备知识及投资组合优化问题的CVaR模型.

定义1(次微分) 设f(x)是n上凸函数,称

∂f(x)={ξ∈n|f(y)≥f(x)+ξT(y-x),∀y∈n}

为f在x点的次微分,向量ξ∈∂f(x)称为f在x处的次梯度,相应不等式称为次梯度不等式.

(1)

为束方法在迭代过程中产生的下一个候选点.其中,μk>0为迫近参数,当割平面近似最小值点与当前稳定中心距离太远时,可以通过减小μk,增大惩罚去除候选点,从而每次迭代都会产生与当前稳定中心较接近的试探点.对xk+1进行下降性检验,若下降充分则执行下降步,否则,执行空步,稳定中心保持不变.

定义3(VaR(风险价值)和CVaR(条件风险价值))[4]假设一投资组合,其投资权重为x=(x1,x2,…,xn)T,y∈n表示投资的损益.假设y的概率密度函数为p(y),损失函数f(x,y)=-xTy，则f(x,y)为随机变量.假设损失变量y服从的分布函数为其中，α为某一临界值,则在置信水平β∈(0,1)给定的情况下，VaR定义为

αβ(x)=min{α|ψ(x,α)≥β}.

CVaR定义为

基于CVaR的投资组合的优化模型一般具有如下形式[5-6]：

(2)

模型：单期投资组合的CVaR模型

令m=E(y),则E[xTy]≥R就是xTm≥R，单期投资组合的CVaR模型为

(3)

问题(3)为凸规划,所以其全局最优解与局部最优解相同,又由于问题(3)为非光滑凸规划问题,因而可利用束方法对其进行求解.一般束方法在求解下一个候选点xk+1时等价于求解一个无约束二次规划子问题,因此,不妨利用指示函数将CVaR模型中的约束集直接添加到二次规划子问题中进行求解.

求解CVaR模型的惩罚束方法：

求解问题(3)的下一个候选点(xk+1,αk+1)相当于求解下述二次规划子问题：

(4)

其中,

问题(4)可以等价的写成

(5)

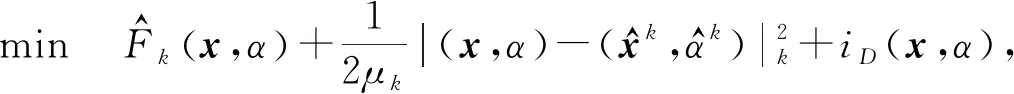
(6)

对于指示函数iD(x,α),利用类似的割平面思想构造以下的模型：

其中,∂iD(xi,αi)=ND(xi,αi)={(z1,z2)|〈(z1,z2),(y1,y2)-(xi,αi)〉≤0,∀(y1,y2)∈D},则问题(5)又可等价表示成

(7)

定义4设(x*,α*)为问题(6)的最优解,令(xk+1,αk+1)=(x*,α*), 将期望下降量定义为

(8)

定义5将

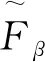
2 对偶问题及一些重要关系

通过研究问题(6)，得到以下主要结论：

定理2.1令(xk+1,αk+1)是问题(6)的唯一解,则

(9)

是下述问题的最优解:

(10)

且下述结论成立：

证问题(6)可以改写成求解下述二次规划问题：

(11)

合并同类项得到：

考虑上述对偶问题.对于每个给定的γl∈Δk,(l=1,2),记

根据最优性条件，

(12)

故结论(9)成立.

即

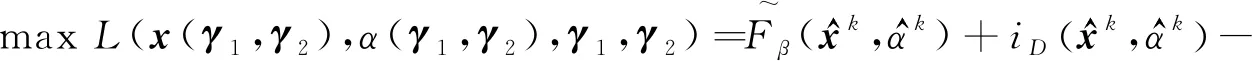
(13)

下面证明结论(2)成立.首先,因为原子问题和对偶子问题没有对偶间隙,故问题(6)的最优值和对偶子问题(13)的最优值相同：

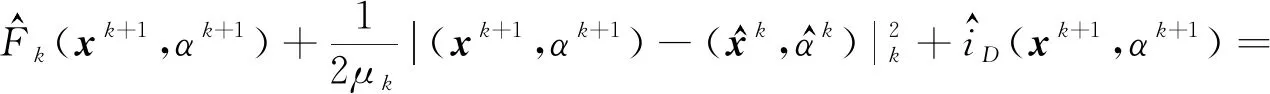
因此, 联立式(7)和式(8),得到

利用式(10),上述不等式还可以写作：

由vk原始定义和结论(2),有

故此结论(3)成立.

3 结 论

本文对CVaR模型的优化问题展开研究,利用迫近思想给出原子问题和对偶子问题的解的显式表示，并且得到了与次梯度和近似次梯度有关的重要结论,这些结论对于分析算法收敛性有至关重要的作用.