诣零幂级数McCoy环
张 万 儒
(河西学院 数学与统计学院,甘肃 张掖 734000)
本文所有的环都是有单位元的结合环.对于环R,用R[x]表示R上的多项式环,R[[x]]表示R上的幂级数环,nil(R)表示R中所有幂零元做成的集合,nil(R)[[x]]表示R[[x]]中系数是幂零元的所有幂级数做成的集合,Mn(R)表示R上的n阶矩阵环.
定义1[1]如果R[x]中任意非零多项式f(x)和g(x),当f(x)g(x)=0时,存在非零元c∈R,使得f(x)c=0(cg(x)=0)成立,则称环R是右(左)McCoy环.如果R既是左McCoy环,又是右McCoy环,则称R是McCoy环.
定义2[2]如果R[[x]]中任意非零幂级数f(x)和g(x),当f(x)g(x)=0时,存在非零元c∈R,使得f(x)c=0(cg(x)=0)成立,则称环R是右(左)幂级数McCoy环.如果R既是左幂级数McCoy环,又是右幂级数McCoy环,则称R是幂级数McCoy环.
幂级数McCoy环是McCoy环,文献[2]中例2.6表明,反之并不成立.
定义3[3]如果R[x]中任意非零多项式f(x)和g(x),当f(x)g(x)∈nil(R)[x]时,存在非零元c∈R,使得f(x)c∈nil(R)[x](cg(x)∈nil(R)[x])成立,则称环R是右(左)诣零McCoy环.如果R既是右诣零McCoy环,又是左诣零McCoy环,则称R是诣零McCoy环.
文献[1,4-7]给出了McCoy环的相关性质和实例;文献[2]研究了幂级数McCoy环;文献[3,8]给出了诣零McCoy环的相关性质和实例.本文在幂级数环中讨论环的诣零McCoy条件,引入了诣零幂级数McCoy环的概念,给出了诣零幂级数McCoy环的例子,并讨论了诣零幂级数McCoy环的基本性质及诣零幂级数McCoy环的扩张.
定义4设R是环,如果对R[[x]]中任意非零幂级数f(x)和g(x),当f(x)g(x)∈nil(R)[[x]]时,存在非零元c∈R,使得f(x)c∈nil(R)[[x]](cg(x)∈nil(R)[[x]])成立,则称R是诣零幂级数右(左)McCoy环.如果R既是右诣零幂级数McCoy环,又是左诣零幂级数McCoy环,则称R是诣零幂级数McCoy环.
设R是环,Tn(R)表示R上的n×n上三角矩阵环.记
按通常的矩阵加法和乘法,Sn(R)和Dn(R)分别构成Tn(R)的子环.
设R是环,RMR是R双模,T(R,M)={(a,x)|a∈R,x∈M}.规定T(R,M)上的加法为对应分量相加,乘法为(a1,x1)(a2,x2)=(a1a2,a1x2+x1a2).按规定的加法和乘法,T(R,M)构成一个环,称为R借助于M的平凡扩张.
定理1设R是环,n≥2是正整数,则下列结论成立:
1)Tn(R)是诣零幂级数McCoy环;
2)Sn(R)是诣零幂级数McCoy环;
3)Dn(R)是诣零幂级数McCoy环;
4)T(R,M)是诣零幂级数McCoy环.
证明:设Eij(1≤i,j≤n)是矩阵单位.取C=E1n∈Tn(R).容易验证:对任意的A∈Tn(R),AC和CA都是Tn(R)中的幂零元.所以Tn(R)是诣零幂级数McCoy环.同理,Sn(R)和Dn(R)也是诣零幂级数McCoy环.
任取0≠(0,m)∈T(R,M).容易验证:对任意的A∈T(R,M),A(0,m)和(0,m)A都是T(R,M)中的幂零元.所以T(R,M)是诣零幂级数McCoy环.
定理2如果R是Reduced环(没有非零幂零元的环),n≥2是正整数,则Mn(R)既不是右诣零McCoy环,也不是左诣零McCoy环,从而Mn(R)不是诣零幂级数McCoy环.
证明:取
容易验证:f(x)g(x)=0∈nil(Mn(R))[x].由于f(x)=E11+E12x+…+Ennxn2-1,如果存在C∈Mn(R),使得f(x)C∈nil(Mn(R))[x],则对任意的1≤i,j≤n,EijC∈nil(Mn(R))成立.不妨设C=(cij)n×n.由于E11C,E12C,…,E1nC∈nil(Mn(R)),而
所以c11,c21,…,cn1∈nil(R).由于R是Reduced环,所以c11=c21=…=cn1=0,从而
同理,由于E21C,E22C,…,E2nC∈nil(Mn(R)),而
所以c12=c22=…=cn2=0.类似地,可证对任意的1≤i,j≤n,cij=0,所以C=0,从而Mn(R)不是右诣零McCoy环.类似可证:Mn(R)也不是左诣零McCoy环.证毕.
根据定理1,可能猜想:当n≥2时,R上的n×n矩阵环Mn(R)也是诣零幂级数McCoy环.定理2 表明这个猜想不成立.
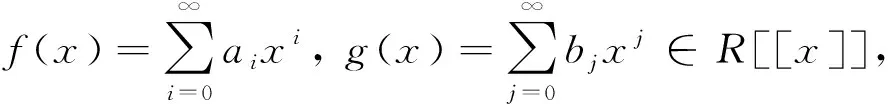
例1设R是环,S=M2(R).取

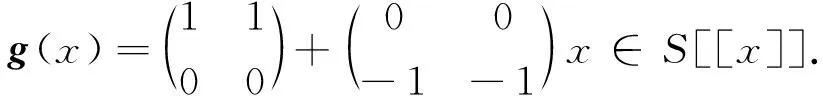
显然,f(x)g(x)=0∈nil(S)[[x]].但

∉nil(S).
所以S不是诣零幂级数Armendariz环.根据文献[9]命题7可知,Tn(S)也不是诣零幂级数Armendariz环.但根据定理1,Tn(S)是诣零幂级数McCoy环.
显然,诣零幂级数Armendariz环是诣零幂级数McCoy环.例1表明,反之并不成立.
例2设R是环,由文献[3]例2.4可知,R上的n×n上三角矩阵环Tn(R)不是右McCoy环,从而不是右幂级数McCoy环.但根据定理1,Tn(R)是右诣零幂级数McCoy环.
例2表明,诣零幂级数McCoy环不是幂级数McCoy环.
定理3右诣零幂级数McCoy环的直积是右诣零幂级数McCoy环.

1) 存在k∈I,使得fk(x)≠0,gk(x)≠0成立.由于Rk是右诣零幂级数McCoy环,因此存在非零元rk∈Rk,使得fk(x)rk∈nil(Rk)[[x]]成立.令r=(ri)i∈I,其中
则0≠r∈R,并且f(x)r∈nil(R)[[x]].
2) 对所有的i∈I,fi(x)≠ 0,gi(x)≠0不能同时成立.由于f(x)≠0,g(x)≠0,因此只有以下两种情形:
① 存在k∈I,使得fk(x)≠0但gk(x)=0.令J={i∈I|fi(x)≠0},则J≠Ø.同时J≠I,否则,所有的gi(x)=0,从而g(x)=0,矛盾.令r=(ri)i∈I,其中
则0≠r∈R,并且f(x)r=0∈nil(R)[[x]].
② 存在k∈I,使得fk(x)=0但gk(x)≠0.与情形①类似可证,存在0≠r∈R,使得f(x)r∈nil(R)[[x]].
所以,R是右诣零McCoy环.
推论1设R是环,e∈R是中心幂等元.如果eR和(1-e)R都是右诣零幂级数McCoy环,则R是右诣零幂级数McCoy环.
例3设R是Reduced环,S=M2(R).根据定理1,T2(S)是右诣零幂级数McCoy环.但由定理2可知,S作为T2(S)的子环却不是右诣零幂级数McCoy环.设
则I是T2(S)的理想,且T2(S)/I≅S不是右诣零幂级数McCoy环.设E是S中的单位矩阵,
则e2=e且eT2(S)e≅S不是右诣零幂级数McCoy环.
例3表明,右诣零幂级数McCoy环的子环和同态象不一定是右诣零幂级数McCoy环,并且如果R是右诣零幂级数McCoy环,e2=e∈R,eRe不一定是右诣零幂级数McCoy环.
命题1设I是环R的理想.如果I⊆nil(R),并且R/I是右诣零幂级数McCoy环,则R是右诣零幂级数McCoy环.

对于0≠f(x)∈R[x],用degf表示f(x)的次数.如果f(x)=0,则规定degf=0.R[x;x-1]表示环R上的Laurent多项式环.
定理4如果环R满足nil(R[x])=nil(R)[x],则R是右诣零McCoy环当且仅当R[x]是右诣零McCoy环.
证明:假设0≠p(y)=f0+f1y+…+fnyn,0≠q(y)=g0+g1y+…+gmym∈R[x][y],使得p(y)q(y)∈nil(R[x])[y],其中fi,gj∈R[x].取正整数k=degf0+…+degfn+degg0+…+deggm+1,f(x)=f0+f1xk+f2x2k+…+fnxnk,g(x)=g0+g1xk+g2x2k+…+gmxmk.则f(x)(g(x))的系数做成的集合和所有fi(x)(gi(x))的系数做成的集合相等.由于p(y)q(y)∈nil(R[x])[y] 且nil(R[x])=nil(R)[x],因此容易验证f(x)g(x)∈nil(R)[x].因为R是右诣零McCoy环,所以存在0≠c∈R,使得f(x)c∈nil(R)[x].从而对任意的0≤i≤n,fic∈nil(R)[x]成立.由于nil(R[x])=nil(R)[x],所以p(y)c∈nil(R[x])[y].从而R[x]是右诣零McCoy环.
设0≠f(x)=a0+a1x+…+anxn,0≠g(x)=b0+b1x+…+bmxm∈R[x],满足f(x)g(x)∈nil(R)[x].令p(y)=a0+(a1x)y+…+(anxn)yn,q(y)=b0+(b1x)y+…+(bmxm)ym∈R[x][y].由于nil(R[x])=nil(R)[x],则p(y)q(y)∈nil(R[x])[y].又由于R[x]是右诣零McCoy环,因此存在0≠c(x)=c0+c1x+…+csxs∈R[x],使得p(y)c(x)∈nil(R[x])[y],从而对任意的0≤i≤n,(aixi)c(x)∈nil(R[x])成立.由于nil(R[x])=nil(R)[x],所以(aixi)c(x)∈nil(R)[x].从而对任意的0≤i≤n和0≤j≤s,aicj∈nil(R).又由于0≠c(x),因此存在0≠ck∈R,使得对任意的0≤i≤n,aick∈nil(R)成立.从而f(x)ck∈nil(R)[x].故R是右诣零McCoy环.
定理5设R是环,下列条件等价:
1)R[x]是右诣零McCoy环;
2)R[x;x-1]是右诣零McCoy环.

2)⟹1).假设0≠f(y)=f0+f1y+…+fnyn,0≠g(y)=g0+g1y+…+gmym∈R[x][y],满足f(y)g(y)∈nil(R[x])[y],其中fi,gj∈R[x].显然f(y)g(y)∈nil(R[x;x-1])[y].又由于R[x;x-1]是右诣零McCoy环,因此存在0≠c(x)∈R[x;x-1],使得f(y)c(x)∈nil(R[x;x-1])[y].由于c(x)∈R[x;x-1],因此存在正整数k,使得c(x)xk=c′(x)∈R[x].容易验证f(y)c′(x)∈nil(R[x])[y].所以R[x]是右诣零McCoy环.
[1] Nielsen P P.Semi-commutativity and the McCoy Condition [J].J Algebra,2006,298(1):134-141.
[2] YANG Shi-zhou,SONG Xue-mei,LIU Zhong-kui.Power-Serieswise McCoy Rings [J].Algebra Colloq,2011,18(2):301-310.
[3] ZHAO Liang,ZHU Xiao-sheng,GU Qin-qin.Nilpotent Elements and McCoy Rings [J].Studia Sci Math Hungar,2012,49(3):326-337.
[4] Camillo V,Nielsen P P.McCoy Rings and Zero Divisors [J].J Pure Appl Algebra,2008,212(3):599-615.
[5] ZHAO Ren-yu,LIU Zhong-kui.Extensions of McCoy Rings [J].Algebra Colloq,2009,16(3):495-502.
[6] Alhevaz A,Moussavi A,Habibi M.On Rings Having McCoy-Like Conditions [J].Comm Algebra,2012,40(4):1195-1221.
[7] Jeon Y C,Kim H K,Kim N K,et al.On a Generalization of the McCoy Condition [J].J Korean Math Soc,2010,47(6):1269-1282.
[8] Antoine R.Nilpotent Elements and Armendariz Rings [J].J Algebra,2008,319(8):3128-3140.
[9] Hizem S.A Note on Nil Power Serieswise Armendariz Rings [J].Rend Circ Mat Palermo,2010,59(1):87-99.

