基于时间序列的管制员眼动数据研究

林思远，胡荣锦，张美玉，王艳军

(1.南京航空航天大学 民航学院，南京 211106；2.国家空管飞行流量管理技术重点实验室，南京 211106；3.北京航空有限责任公司，北京 100621)

民用航空运输凭借其安全、快捷、舒适、不受地形限制的优点，在交通运输业中占有独特的地位.空中交通管制员(Air Traffic Controllers，以下简称管制员)在空管系统中处于重要的位置，监视航空器在本管制责任区内的运行，与飞行员进行通信，解决航空器之间的潜在冲突，确保整个航空运输系统安全、高效的运行[1].判断评估管制员的行为一直是航空领域研究的难点.管制环境是一个复杂的系统，正确判断和预测管制员行为十分困难，影响因素复杂，且所得的结果准确性很难定量判断.

眼睛是人类获取外部信息最重要的通道[2]，近20年，大量的研究对眼球运动进行了探索，并以此检查潜在的神经认知功能[3].注视会影响我们在日常任务中行动的准确性.人类的眼睛定期通过眼跳运动来扫描环境，并注视相关区域，从而为视觉信息的分采样提供支持[4].人类注视的位置是由知觉、认知和运动活动之间持续的相互作用决定的，这些相互作用促进了相关信息的选择和处理[5-6].

在空管领域，眼动追踪常用于评估管制员的工作负荷、疲劳程度、视觉搜索与注意力分配.眼动行为是心理活动的外在表现，眼动指标的时空特性能够表征管制员信息搜索过程中的行为.管制员获取信息的方式主要通过观察雷达屏幕，因而管制员眼动行为的时空特性反映了管制员对管制环境的认知及注意力的分配状况，管制员面对不同的管制场景有不同的应激行为.Ahlstrom[7]等人发现随着飞机数量的增加，管制员工作负荷也随之增加，眨眼持续时间减少而瞳孔直径增加.Stasi[8]研究了眼跳速度与认知之间的关系.Imants[9]等人发现在同一任务场景下，不同管制员的搜索策略不尽相同.Marchitto[10]等人研究了在冲突监测任务中的管制员眼动行为.Kang[11]等人发现在管制任务中，高效的专家眼动行为模式对于培训新手大有裨益.Yoshida[12]等人发现在管制任务中，航班标牌颜色显著性会影响管制员的眼动行为.陈健[13]等人发现眨眼数据和PERCLOS能够有效评估管制员的疲劳状态.靳慧斌[14-15]等人研究了管制员工作负荷的实时监测方法和眼动指标监测疲劳的有效性.王燕青[16]等人发现不同流量大小下，管制员的眼动行为存在显著性差异，同时新手管制员和专家管制员眼动模式也存在差异.王超[17]等人发现管制员对进场飞机和飞机标牌的关注度很高.

国内外基于管制员眼动行为的研究取得了较多的成果，但很少有研究将眼动行为作为一个时间序列进行分析.为此，本文基于TDS算法与MF-DFA算法，研究分析了管制员的眼动行为数据.

1 实验设计

1.1 实验被试

10名来自南京航空航天大学的管制专业大四本科生和2名来自华东空管局江苏分局的管制员参加了本次实验.

1.2 实验场景设计

为避免其他因素对制员管眼动数据的影响，突出管制场景属性中航空器数量，本次实验将复杂的管制扇区场景进行简化，抽取所需的场景特征，设置“人在环路”(Human-in-the-loop)的管制模拟实验.实验场景根据管制员的工作环境进行模拟，分为不同流量的4个模拟实验场景，航空器数量分别为4、8、12、16架次，通过计算机随机自动语音播报，被试需要寻找目标航空器.模拟实验场景中，航空器信息包括航空器呼号、当前高度及目标高度.图1为8架次航空器实验场景图.

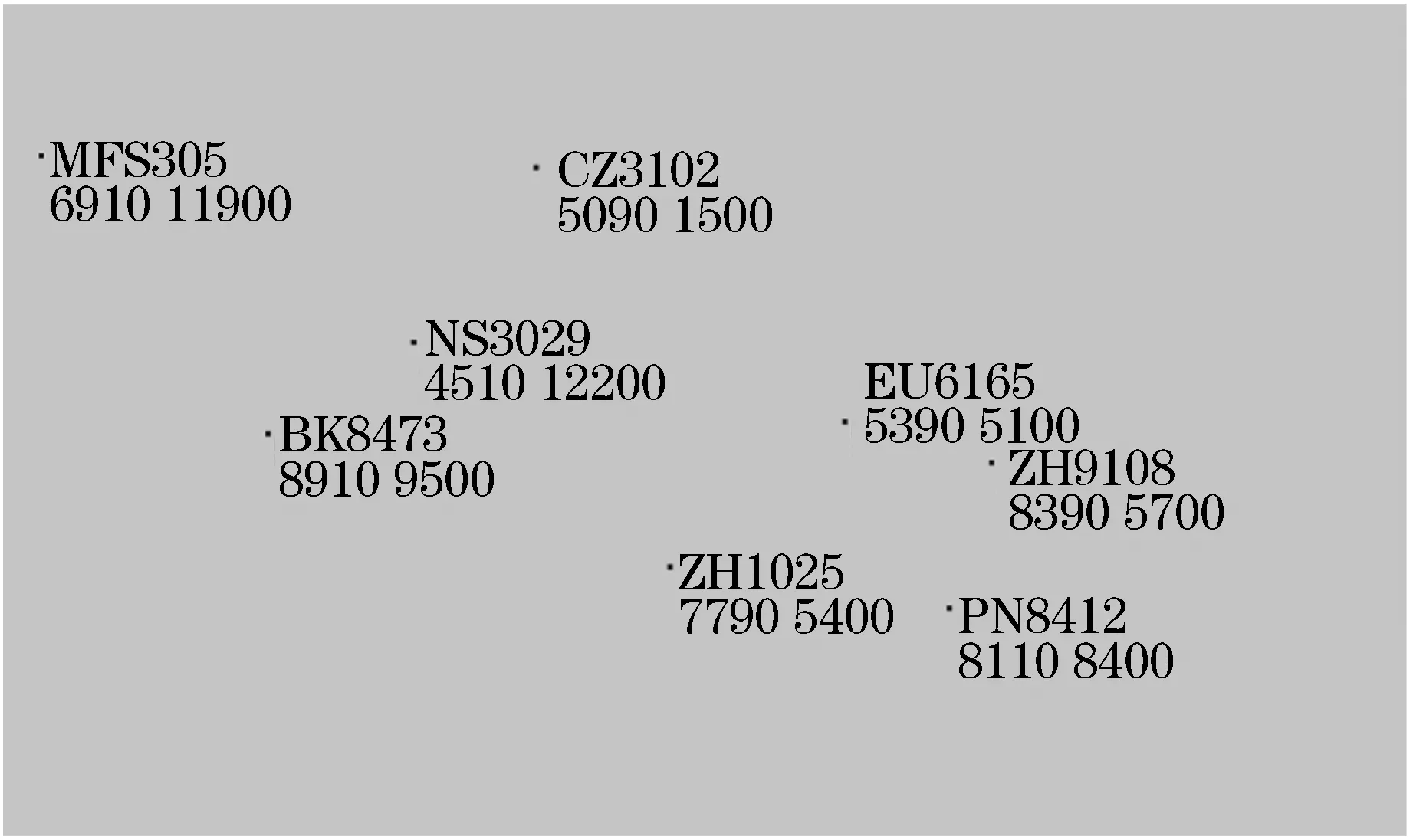
图1 8架次航空器实验场景图

1.3 实验步骤

1)在实验开始前询问被试相关情况，并告知此次实验的内容、操作与目的；

2)被试坐在屏幕前，调整座椅至本人舒适；

3)开始实验前测试并校准眼动仪，测试生理参数仪；

4)根据4、8、12、16架次航空器场景依次进行实验，每场实验约5 min，采集管制员在实验过程中的眼动与生理数据；

5)待所有实验完成后，实验结束.

1.4 采集设备与数据处理方法

本次实验中采用Seeing Machines 生产的faceLAB5.0眼动仪采集被试的眼动数据，采样频率为60Hz；采用生物反馈BFB2000肌电和多参数模块采集被试的生理相关数据，包括肌电、皮电、脉搏与皮温，采样频率为200 Hz.

本文主要分析的眼动行为是注视行为和扫视行为，需利用眼动指标区分算法提取并计算眼动注视、扫视行为指标.为了区分原始数据的注视点与扫视点，本文采用了Krassanakis[18]的眼动注视识别算法，计算得到注视持续时间、扫视持续时间与扫视角速度.

2 眼动数据与生理数据的关联性

2.1 TDS算法

人体可以看做是一个复杂系统，子系统之间可能将不断发生相互作用从而导致整个系统的改变.Bashan[19]等人提出了时间延迟稳定性(Time Delay Stability, TDS)算法量化各个子系统之间的关联性.在该算法中，若两类指标具有基本相似的延迟时间，则表明这两类指标之间具有较强的关联性.

下面给出TDS算法的步骤：

1)将目标系统X和Y的输出数据记为[a]和[b]，长度为S；

2)将数据[a]和[b]分成等长为K的SK重叠段，每个子片段为v，每次子片段v选择重叠K/2，其中SK=[2S/K]-1；

3)将每段v归一化为无量纲数据，确保数据[a]和[b]之间的估计耦合不受其相对幅度的影响；

4)通过周期性边界条件计算互相关函数：

(1)

其中：v=1,…,SK；

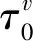
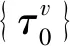
2.2 数据结果

由于TDS算法需要时间序列的一致性，故选取眼动指标中的瞳孔直径和眨眼频率两个指标分别计算其与生理相关参数的时间延迟稳定性.图2为瞳孔直径与相关生理指标之间的时间延迟稳定性，横坐标表示时间节点，纵坐标表示指标发生延迟的时间.图2(A)中，在10～200 s内瞳孔直径与肌电具有稳定的时间延迟1～2 s，虽然在95～115 s中间有波动，但其影响可以忽略.在图2(B)中，在45～140 s内，瞳孔直径与脉搏信号变化较稳定.在图2(C)中，在40～120 s内，瞳孔直径与皮温具有稳定的时间延迟6～7 s.在图2(D)中，在15～175 s内，瞳孔直径与皮电具有稳定的时间延迟3～5 s.图2说明在45～120 s内，瞳孔直径的变化都会引起相关生理指标的稳定时间延迟变化，说明瞳孔直径与肌电、脉搏、皮温与皮电之间的联系较为紧密.

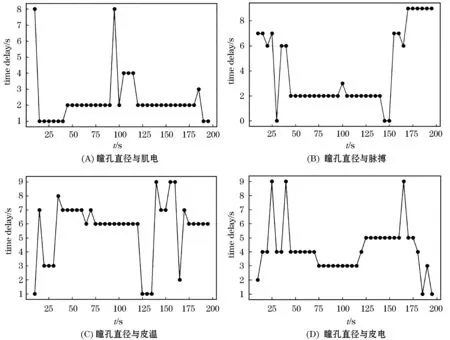
图2 瞳孔直径与相关生理指标之间的时间延迟稳定性

图3反映了一个管制员的眨眼频率与相关生理指标之间的时间延迟稳定性.在图3(A)中，在80～160 s内，眨眼频率与皮温具有稳定的时间延迟7～8 s，其他时间段内没有明显的时间延迟.在图3(B)中，在60～155 s，眨眼频率与肌电具有稳定的时间延迟3～4 s.

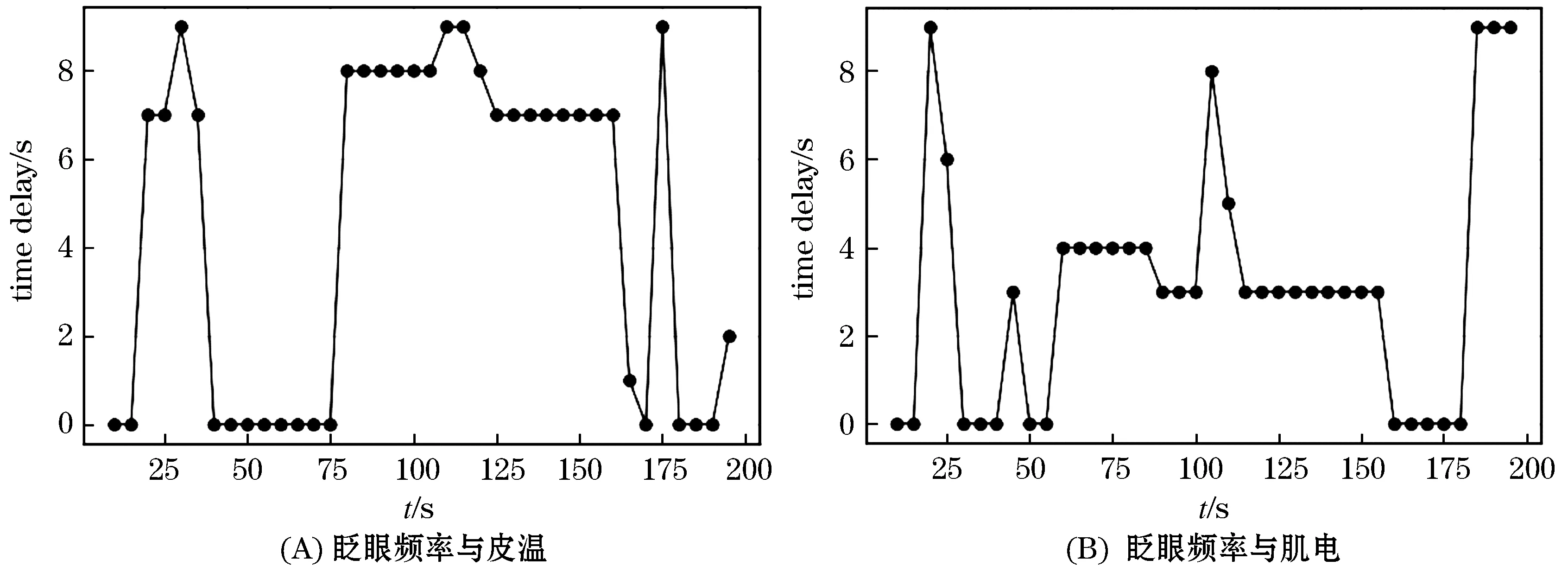
图3 眨眼频率与相关生理指标之间的时间延迟稳定性

综上，根据TDS算法得出的结果，瞳孔直径、眨眼频率两指标数据分别与生理系统中肌电、皮电、皮温等指标数据有较长的稳定时间延迟，说明眼动系统与生理系统之间存在着较强的关联性.因此，生理系统可以在一定程度上表征眼动系统，为分析管制员眼动行为提供参考.

3 眼动数据的多重分形特征

3.1 MF-DFA算法

眼动数据呈非线性变化.实验中采集的眼动数据混杂着一些噪声数据，必须消除噪声数据的干扰趋势波，才能更好地呈现眼动数据的自相似特征，获得各数据波形变化特征.多重分形去趋势波(Multi-fractal Detrended Fluctuation Analysis，MF-DFA)是分析波形复杂度的一种方法[20]，能够反映隐藏在信号内部的信息.

下面给出MF-DFA算法的步骤：

1)取长度为N的时间序列[xk]，k=1,2,…,N，求该序列的均值：

(2)

2)构造均值和序列，确定其累积离差：

(3)

3)将生成的C(i)序列划分成Ns个互不相同的区间，每个区间含有s个数据，其中：Ns=int(N/s)；

4)对于划分的每个小区间v(v=1,2,…,NS)内的s个数据，利用最小二乘法进行多项式拟合，得到阶数为k的拟合多项式：

cv(i)=a1ik+a2ik-1+…aki+ak+1

(4)

5)求均方误差F2(s,v)，计算区间为v(v=1,2,…,NS)：

(5)

6)求去趋势后的F2(s,v)均值，求取q阶波动函数Fq(s)：

当q=0时，波动函数为：

(6)

当q≠0时，波动函数为：

(7)

其中：Fq(s)是序列数据长度s和阶数q的函数，表示不同的q描述信号不同波动程度对Fq(s)的影响，Fq(s)随着s的增大呈幂律增长，其关系为：

Fq(s)∝sh(q)

(8)

其中：h(q)称为广义Hurst指数，即为logFq(s)～log函数式中的变化斜率；当q=2时，MF-DFA成为DFA;当q>0时，Fq(s)主要反映信号波形中大波动状况，当q<0时，Fq(s)主要反映信号波形中小波动状况.当所选序列[xk]，k=1,2,…,N为单一分形时，F2(s,v)在所选区间标度行为一致，使h(q)成为独立于q的常数；当h(q)为随q变化的函数时，则表明该序列具有多重分形特征.

但是，上述MF-DFA描述方法只能确定广义Hurst指数h(q)为正时的信号性质，当h(q)趋近于0时，该信号就会表现出较强的逆相关，这时MF-DFA算法不能准确地分析信号的性质，此时需要修正MF-DFA算法.

下面给出修正MF-DFA算法的过程步骤：

1)在MF-DFA算法过程的第一步求两次累积离差：

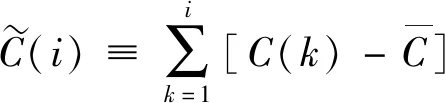
(9)

2)其后计算步骤如MF-DFA算法的过程步骤3～5，得到广义波动函数

(10)

对于大标度有:

(11)

对于时间序列的广义Hurst指数和多重分形理论中的标度指数τ(q)之间满足：

τ(q)=qh(q)-1

(12)

3)根据勒让德变换：

α=τ′(q)

(13)

和

f(α)=qα-τ(q)

(14)

可以得出τ(q)、α和多重分形谱f(α)之间的关系：

(15)

和

f(α)=q[α-h(q) ]+1

(16)

MF-DFA方法中波动函数取值范围为[-20,20].

3.2 数据结果

3.2.1 注视持续时间

图4为不同航空器数量下的注视持续时间序列Fq(s)～s的双对数图，各个子图中的曲线自上而下，其阶数q是逐渐减小的，各个曲线的斜率构成了图4(A)广义Hurst指数曲线.当q从-20增加到+20时，注视持续时间的广义Hurst指数h(q)曲线均依赖q随之下降，即h(q)不为常数，说明注视持续时间在图形上具有自相似性，其也存在显著的多重分形特征，波动函数符合幂律分布.下节不再重复列出其Fq(s)～s的双对数图.

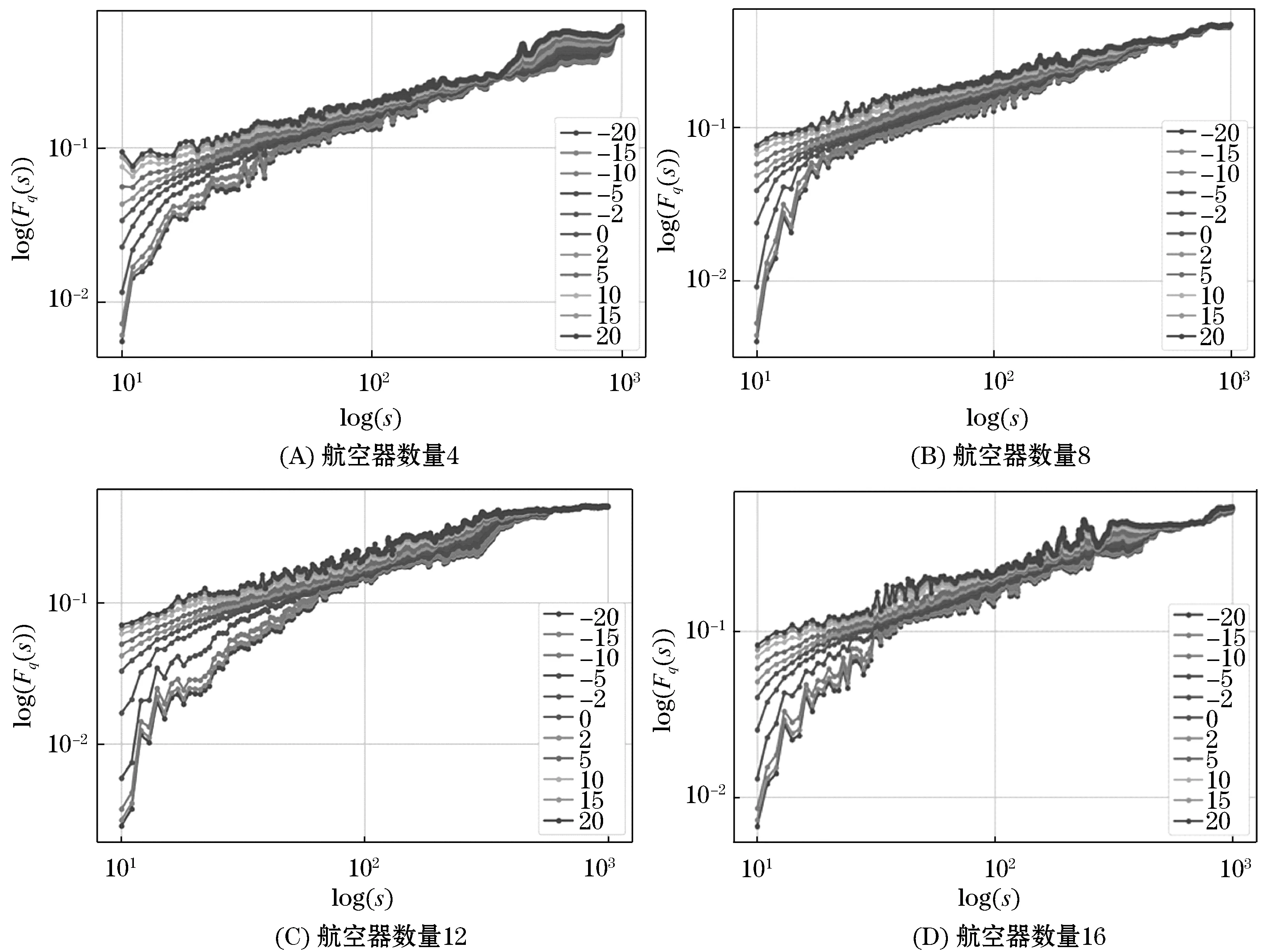
图4 不同航空器数量下注视持续时间的波动函数图

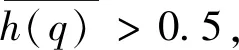
根据多重分形理论，奇异值α反映了信号局部变化的趋势.由图5(B)多重分形奇异谱和表1得随着航空器数量的增加，多重分形谱宽Δα值逐渐增加，而分形维数差Δf逐渐减小，且Δf<0，说明注视持续时间指标局部变化越强烈.波动幅度越大，振动信号波谷数目将多于波峰数目.

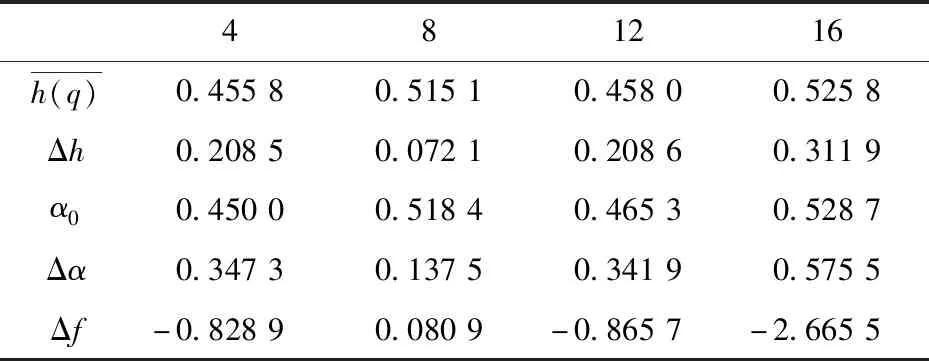
表1 不同航空器数量下注视持续时间MF-DFA参数

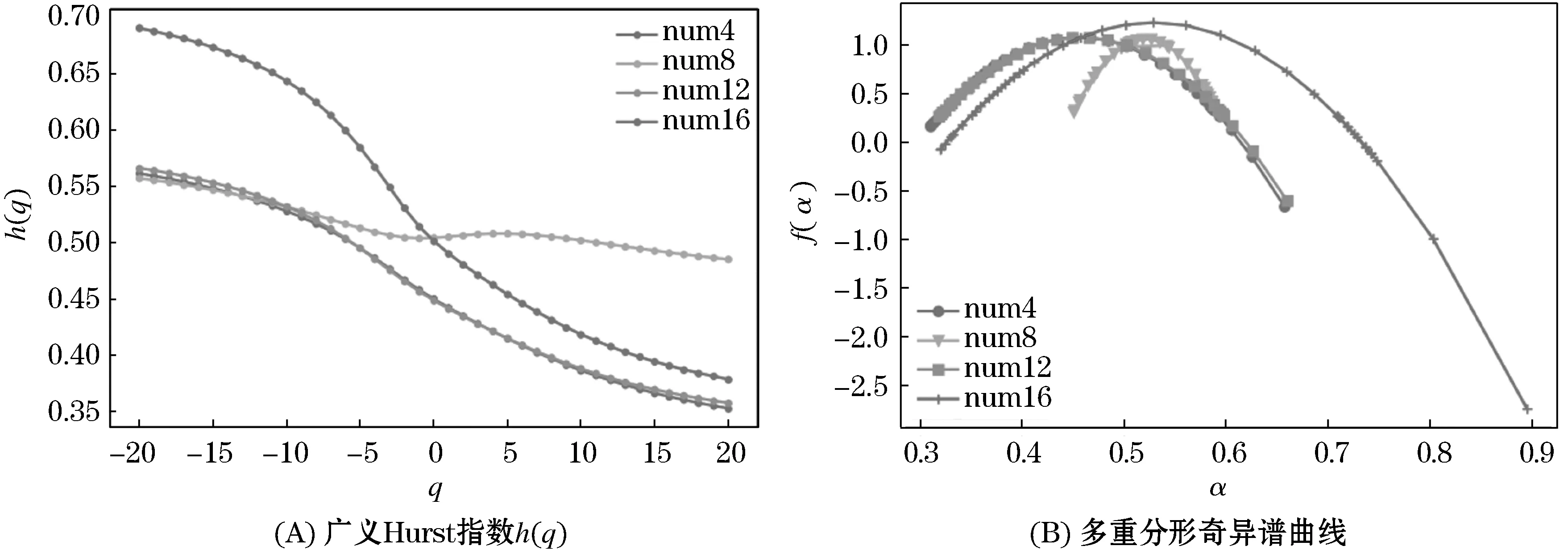
图5 不同航空器数量下注视持续时间的广义Hurst指数和奇异谱曲线

3.2.2 扫视持续时间

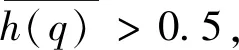
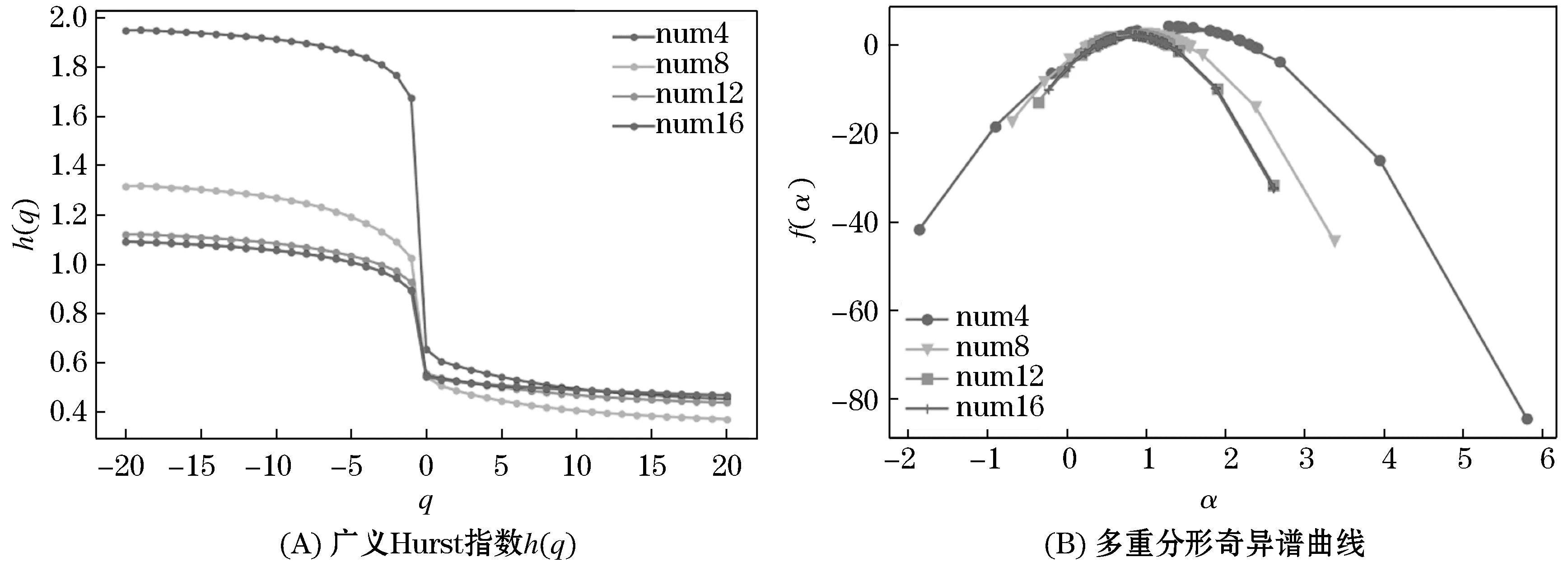
图6 不同航空器数量下扫视持续时间的广义Hurst指数和奇异谱曲线

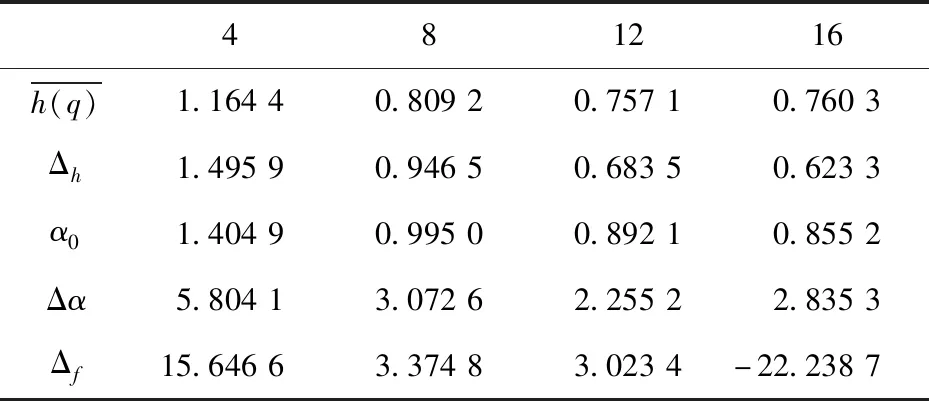
表2 不同航空器数量下扫视持续时间MF-DFA参数

综上，注视持续时间与扫视持续时间的广义Hurst指数都随着阶数q的增加而减少，说明了两种眼动行为都是长程正相关，且都符合幂律分布，这种长程正相关说明了管制员过去的眼动行为会影响将来的眼动行为.总体来说，随着航空器数量的增加，奇异谱的宽度减少，说明航空器数量增加会导致管制员抗外界干扰能力的减弱.这个发现是符合客观规律的，航空器数量增加时，航空器分布复杂性也同样增加，这会占用更多的管制员认知资源，但管制员的认知资源是有限的，航空器数量的增加更容易导致管制员疲劳.

4 结 语

本文分别利用TDS算法与MF-DFA算法分析了管制员在实验过程中的眼动数据与生理数据.结果表明在TDS算法分析中，眼动系统与生理系统之间存在着较强的关联性，生理系统数据可以在一定程度上表征眼动系统数据，为管制员眼动行为分析提供参考，评估管制员在工作过程中的状态.在MF-DFA算法分析中，注视持续时间、扫视角速度与扫视持续时间的波动函数都符合幂律分布，并且随着航空器数量的增加，管制员注视持续时间的多重分形增强，扫视角速度的多重分形减弱，扫视持续时间的多重分形减弱.说明了管制员过去的眼动行为会影响将来的眼动行为，同时航空器数量增加会导致管制员抗外界干扰能力的减弱.分析管制员在执勤过程中眼动数据有助于揭示与理解管制员的行为，本项研究对航空安全、管制员疲劳检测和未来空管系统的设计制造有着重要的意义.

为了深入揭示管制员眼动行为，后续研究将注重以下三个方面：1)在MF-DFA算法分析中不仅局限于眼动数据，将进一步分析管制员相关生理数据和脑电数据的多重分形特征；2)进一步研究生理参数如何表征管制员眼动行为数据；3)研究管制员之前的眼动行为如何影响之后的眼动行为.