一种基于等差鉴别的改进的SDIF分选算法

张忠民，符 逸

(哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001)

随着微电子技术的快速发展，各种复杂体制雷达的涌现，现阶段的电子战所面临的电磁空间愈发恶劣，为雷达信号的分选带来了巨大的挑战[1].序列差直方图SDIF是工程中应用最为广泛的雷达信号分选算法[2].SDIF算法运算量较小，对随机干扰脉冲和脉冲丢失等不敏感，无论是PRI固定，还是PRI抖动和PRI参差等PRI调制雷达信号都可以利用该算法进行分选[3].其中，PRI抖动信号是指信号的PRI在某一固定值附近随机变化，变化量即抖动量，一般服从高斯分布或均匀分布，可作为电子保护措施以对抗干扰.PRI参差雷达具有一个以上的PRI，即存在一个PRI集合，通过依次周期性选择PRI集合中的PRI值来生成脉冲序列，PRI的重复周期称为骨架周期，而骨架周期内的各PRI称为子周期.这种雷达一般用于消除距离模糊和速度模糊[4-5].

文献[6]中提出的一种子周期等差的参差雷达设计方法，使雷达信号可以扰乱敌方的信号分选，对抗敌方的电子侦察系统，提高自身的反侦察能力，而己方接收机若仍使用传统的SDIF算法进行信号分选，将出现增批的情况，即认为有多部固定PRI的雷达，影响了己方的信号分选能力.因此为了在保证反侦察能力的同时提高己方的信号分选能力，本文提出了一种基于PRI周期鉴别的改进的SDIF分选算法.

1 基于SDIF的参差信号分选

1.1 SDIF算法原理

SDIF算法遵从了累计差直方图(CDIF)算法的基本思路：通过统计到达时间差值(Time Difference of Arrival，DTOA)得到差值直方图，使用指数形式的门限进行候选PRI的选取.由于去除了需要多倍DTOA超过门限的限定，避免了CDIF中每一级差值直方图都要累积而导致的计算量过大的问题[7-8].SDIF算法步骤如下：

1)记录一定的观测时间内所有脉冲的到达时间(Time of Arrival，TOA)，存储在缓冲器中，统计TOA序列的C阶序列差直方图，直方图的横坐标为考虑测量误差和抖动的情况下C阶DTOA的所有值，纵坐标为每一个DTOA值对应的脉冲间隔数.由于一般只考虑最高三阶序列差，设置C的最大取值为3.

2)设置合适的判决门限Tthr，统计直方图中超过门限的C阶DTOA.C阶序列差直方图对应的门限曲线表示为：

Tthr(τ)=x(E-C)e-τ/kN

(1)

其中：E是观察时间内脉冲的个数，k∈[0, 1]，N为直方图上最大DTOA值，常数x为经验值，可根据实际情况进行调整.若C=1且有多个差值的统计超过门限，或者没有超过门限的差值，则需要计算C+1阶序列差值直方图.否则将超过门限的差值作为潜在PRI序列，执行步骤3)；循环执行步骤2)直至C已达到设置的最大值；

3) 遍历潜在PRI序列，进行脉冲搜索，即以某个脉冲为基础脉冲，潜在PRI为间隔，若能够连续搜到3个或3个以上的脉冲则搜索成功，且该潜在PRI为PRI真实值，并存储连续搜索到的脉冲序列，同时缓冲器中的脉冲序列移除搜索到的间隔为潜在PRI的脉冲序列；否则脉冲搜索失败，计算C+1阶序列差直方图，执行步骤2)；

4) 缓冲器中的脉冲序列再执行步骤1)，直到脉冲个数小于5，得到所有PRI.若得到的PRI各不相同或差异较大，则判别为每个PRI对应一部固定PRI雷达；若有两个或两个以上的PRI相同或差异很小，该PRI的近似值记为T1，则可能对应一部骨架周期为T的参差雷达，执行步骤5)；

5) 将相同或接近的PRI所对应的搜索到的脉冲序列按照TOA合并为一个序列，计算一阶差直方图，同样按照步骤2)中的门限曲线进行判决，若只有一个差值的统计值超过门限，则判定为这些PRI各自对应一个固定PRI雷达；否则提取统计值超过门限的所有差值，若这些差值的和等于T，则判定为这些PRI是同一部参差雷达的子PRI，否则判定为这些PRI各自对应一个固定PRI雷达[9].

1.2 参差PRI雷达信号

参差PRI雷达信号中包含了多个子PRI值，在实际的工程应用中子PRI的个数为2～7之间[10]，通过循环往复的使用子PRI集合中的值生成参差PRI脉冲序列.设子PRI个数为m,第n个PRI可表示为：

PRIn=PRIk,k=n…m

(2)

通过式(2)可以进一步得到第n个脉冲的到达时间可以表示为：

TOAn=TOAn-1+PRIn-1+ωn

(3)

其中：ωn为TOAn的测量误差.各子PRI之和称之为参差PRI雷达信号的骨架周期或者帧周期[11].

1.3 参差分析

在实际的工程应用中，通常是先对待分选的脉冲序列根据其载频、到达角、脉宽等参数利用K-Means等聚类算法进行预分选[12-13]，得到若干个载频、到达角、脉宽等参数相近的簇群[14]，然后再通过SDIF等主分选算法对预分选得到的每一个簇群进行主分选[3].如果待分选的脉冲序列是由PRI参差的雷达产生的，通过SDIF算法我们将得到多部PRI、载频、到达角、脉宽等参数接近的雷达.而且该PRI值就是参差雷达的骨架周期.参差分析流程图如图1所示.

2 抗SDIF分选参差信号的分选算法

通过前面的分析可以得到，利用SDIF算法对参差PRI雷达信号进行正确分选有两个关键点：

1)通过SDIF算法进行信号分选会得到多部PRI值相近的固定PRI雷达.

2)进入参差鉴别，进一步确定是多部固定PRI雷达还是一部参差PRI雷达.

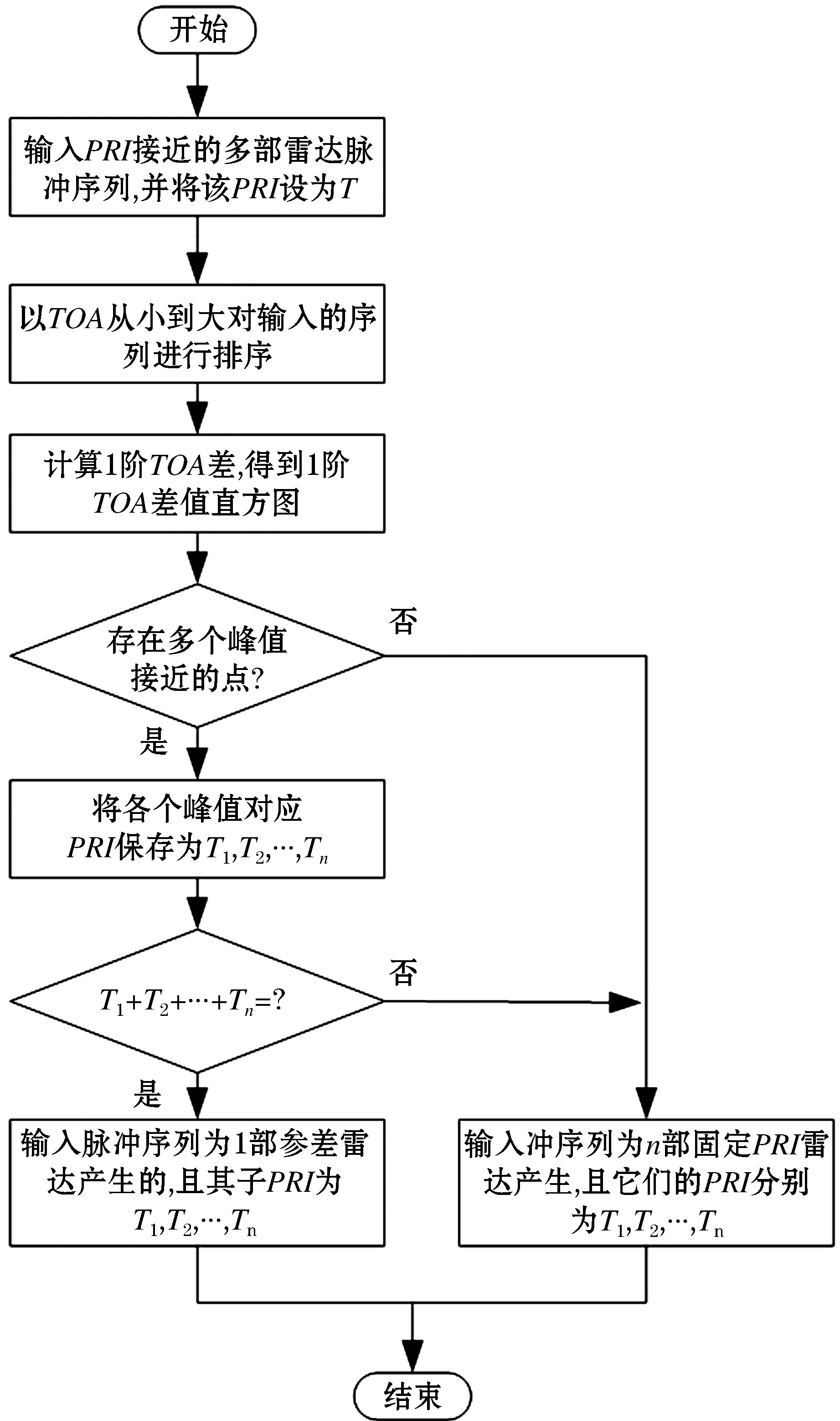
图1 参差分析流程图

如果上述两个关键点中的任意一点不能够满足，那么将不能得到正确的分选结果.为了破坏关键点1中的分选出多部PRI值相近的固定雷达这一条件，可以通过选取适当的子PRI值来使得SDIF算法分选出多部PRI值不同的雷达，如果出现了多部PRI值不同的雷达，就不会进行参差鉴别，这样就会导致分选结果增批.为了达到成功分选出多部PRI值不同的雷达这一目的，子PRI值必须要满足以下两个条件：

1)选取的子PRI值能够在进行二级或二级以上直方图统计时出现虚假峰值，即要求出现不等于骨架周期的峰值.

2)对该虚假峰值进行序列搜索时，能够成功提取出脉冲.

根据上述条件，文献[6]中出了一种抗SDIF分选的脉冲重复间隔参差设计方法.并给出了3～7参差雷达信号的设计规则，该方法要求n参差雷达信号的各子PRI之间呈等间隔递增关系，类似于PRI滑变的情况，即：

PRIi+1=PRIi+Δ,i=1,…,n-1

(4)

还需满足以下条件：

1)二级或二级以上的直方图中虚假峰值都能过检测门限

2)3参差信号，Δ=PRIl(2级直方图峰值对应的PRI进行序列搜索时会提取出虚假序列).

3)4参差信号，对Δ取值无其他要求.

4)5参差信号，Δ=PRIl/4(2级直方图峰值对应的PRI进行序列搜索时会提取出虚假序列).

5)6参差信号，Δ=2PRIl/3 (2级直方图峰值对应的PRI进行序列搜索时会提取出虚假序列).

6)7参差信号，Δ需要满足如下条件之一，即：

①Δ=3PRIl(2级直方图峰值对应的PRI进行序列搜索时会提取出虚假序列).

②Δ=PRIl/9、Δ=PRIl/3或Δ=PRll(3级直方图峰值对应的PRI进行序列搜索时会提出虚假序列).

通过仿真实验表明,该设计方法会使得传统SDIF出现增批现象.

3 基于等差鉴别的改进的SDIF分选算法

根据参差雷达信号的设计原理可知，参差雷达信号是按照一定的排列顺序周期性地使用各子PRI，这就会使得在对参差雷达信号做一阶TOA差值统计时，各子PRI对应的脉冲对个数相近.因此，我们可以在SDIF分选算法的每一次一阶TOA差值统计后加入等差鉴别，等差鉴别的流程图如图2所示.

图2中等差鉴别主要包括最长等差子序列搜索和序列搜索两部分.通过寻找出一阶潜在PRI序列中的峰值相近且TOA差值呈等差递增的子序列，作为潜在参差雷达的子PRI序列.然后再通过以潜在参差雷达的骨架周期为潜在PRI进行序列搜索，若搜索成功，说明待该潜在参差雷达信号的确存在与待分选的脉冲序列中.最后将该参差雷达信号提取出来.

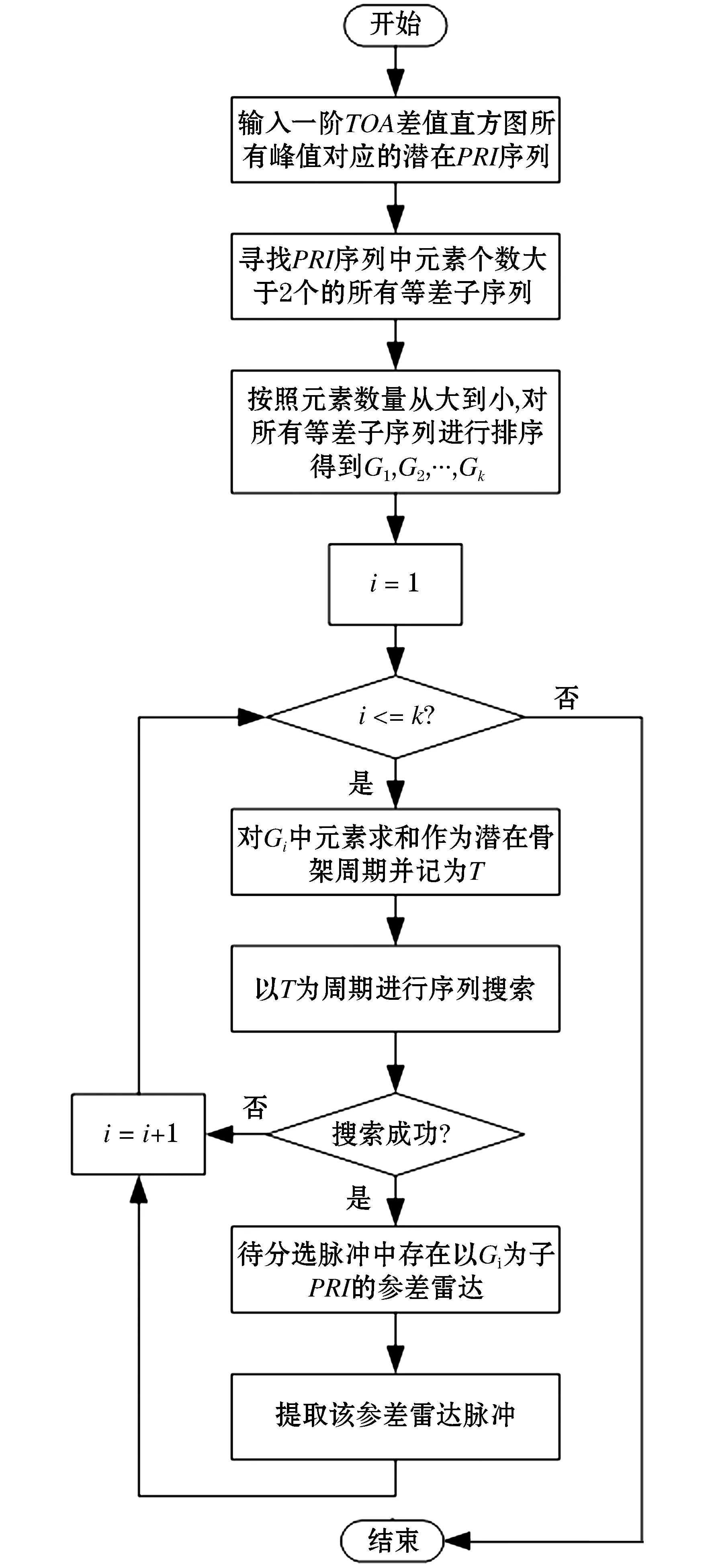
图2 等差鉴别流程图

4 仿真结果与分析

本节主要是对传统的SDIF算法与本文提出的基于PRI等差鉴别的改进的SDIF信号分选算法进行对比仿真验证.设观测时间为20 ms，TOA测量误差为50 ns，序列搜索容限为1 μs，直方图PRI分析范围为0.1～1 000 μs，直方图统计间隔为0.5 μs，SDIF检测门限中的相关参数设置为：x= 0.8；k= 0.1;N= 1 000.

仿真场景设置如表1所示, 所有场景中的参差雷达信号均满足抗SDIF算法分选的设计要求.为了减小测量TOA时产生的误差对直方图统计的结果的影响，本文采用了文献[14]中的方法将相邻直方图间隔的脉冲个数进行合并.

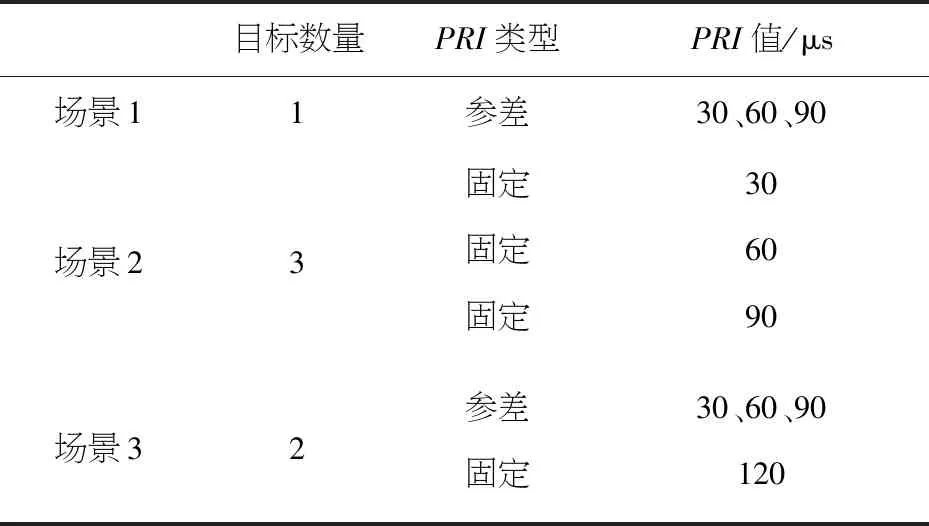
表1 仿真场景设置

场景1的TOA差值直方图统计结果图如图3所示.

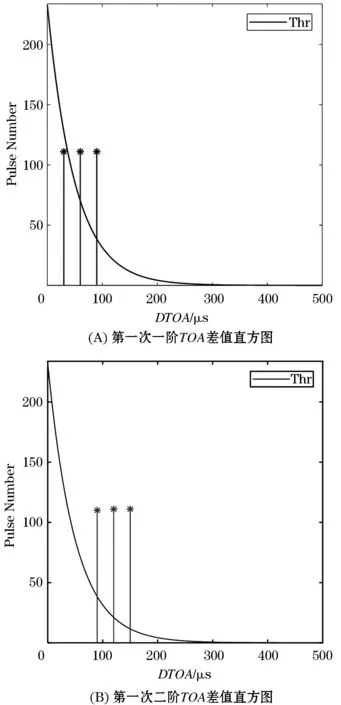
图3 场景1TOA差值直方图统计图

传统的SDIF算法分选：

由图3(A)可知，在一阶TOA差值直方图中存在两个超过检测门限的峰值，故不会进行序列搜索，而是继续进行下一阶TOA差值直方图统计.图3(B)中在 90、130、150 μs处出现峰值，且峰值均超过检测门限.在传统的SDIF算法流程中，将对这三个潜在PRI进行序列搜索.序列搜索过程如图4所示.

由图4(A)可以得到序列搜索将会提取出一部PRI为90 μs的固定PRI雷达，剩余的脉冲如图4(B)所示，其间隔正好为180 μs，因此，在以180 μs为潜在PRI进行序列搜索时，可以成功提取一部固定PRI雷达.

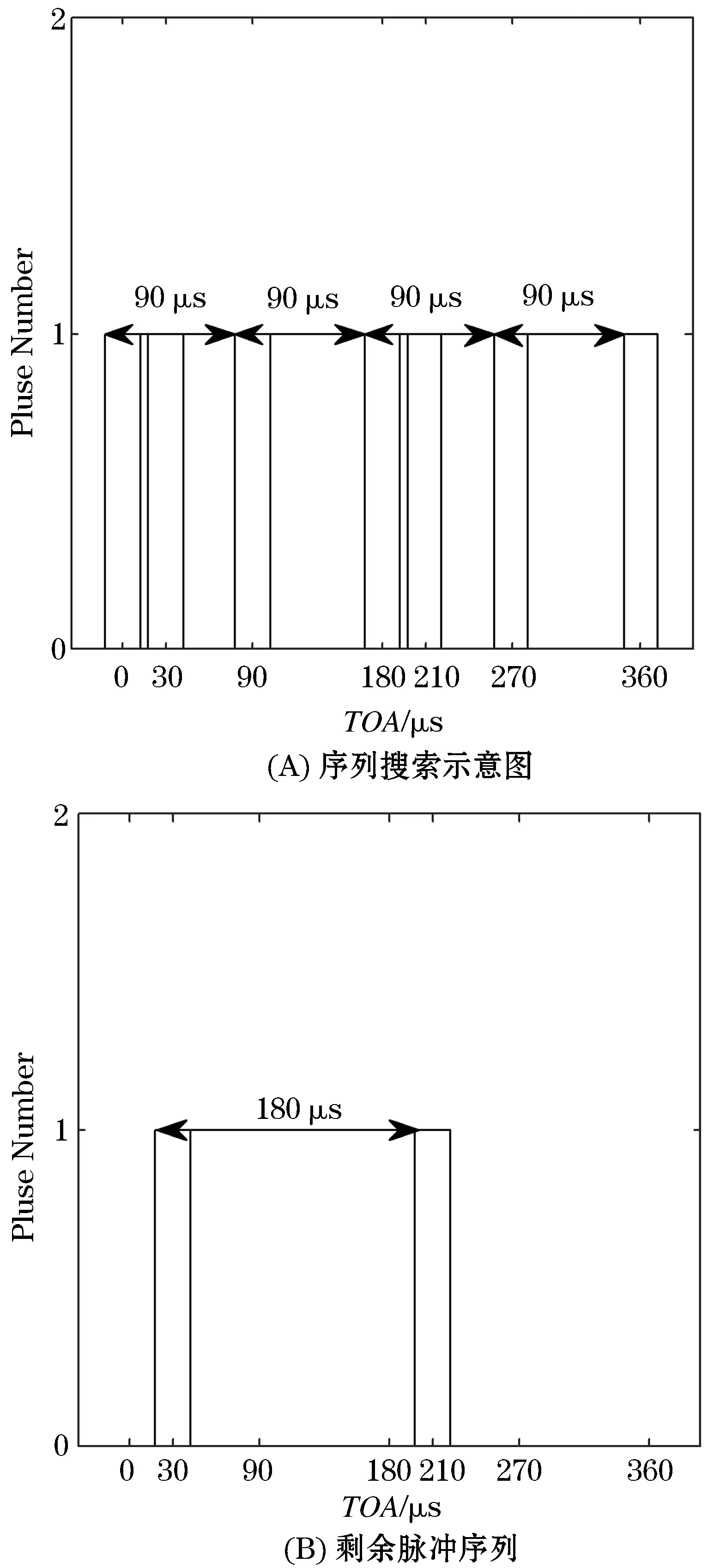
图4 场景1传统SDIF序列搜索

改进的SDIF分选算法：

在进行一阶TOA差值直方图统计后，将进行等差鉴别，由图3可知,一阶TOA差值直方图中所有峰值对应的TOA差值为30、60、90 μs.等差鉴别得到其潜在骨架周期为180 μs，以180 μs为间隔进行序列搜索如图5所示.

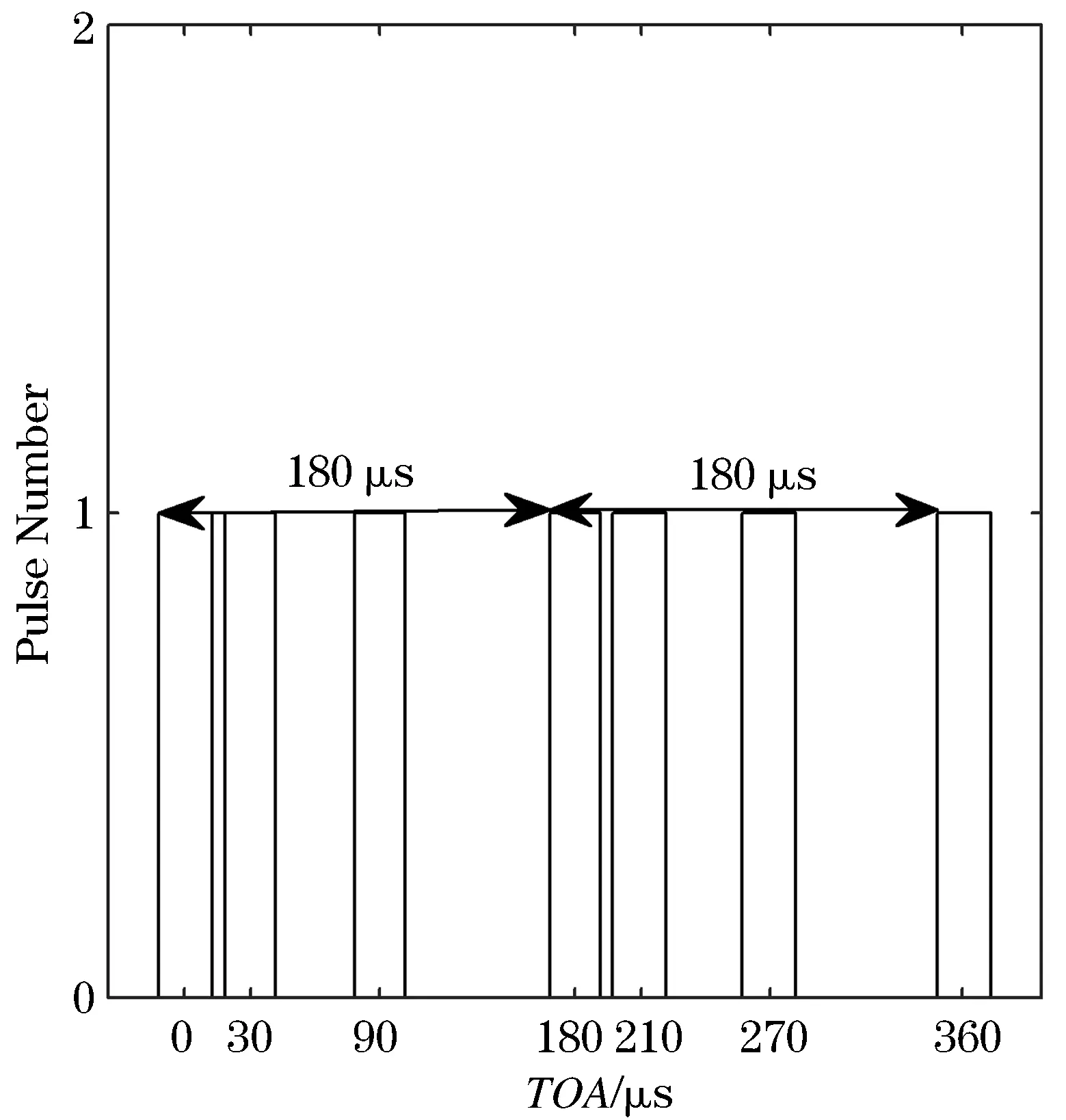
图5 场景1改进SDIF序列搜索示意图

由图5可知,以180 μs为间隔能够成功搜索到序列，因此输入脉冲序列中存在一部以30、60、90 μs为子PRI的参差雷达.

场景1中传统SDIF分选算法结果和改进后的SDIF算法分选结果如表2所示.

表2 场景1中改进前后雷达信号分选结果比较

从表2可以看出，在场景1中，改进前的SDIF算法分选结果不仅出现了增批现象，而且目标的PRI类型和PRI参数都出现了错误.而改进后的SDIF算法分选结果完全正确.

由于场景2中3部雷达都为固定雷达，因此传统的SDIF算法能够将其正确分选.接下来将验证本文提出的算法能否将其正确分选.场景2中的TOA差值图统计结果如图6所示.由图6(A)可知，在一阶TOA差值直方图中仅在TOA差值等于0、30 μs处出现了峰值，没有满足要求的等差子序列.因此将以30 μs为间隔进行序列搜索，并成功分选出PRI为30 μs的固定PRI雷达.继续对剩余脉冲做一阶TOA差值直方图统计，结果为图6(B)所示.由图6(B)可知在DTOA等于 0、30、60 μs处出现峰值，虽然0、30、60 μs存在元素个数大于2的等差子序列，但PRI显然是大于0的，所以有效的PRI峰值仅有30、60 μs两个，故仍然没有满足要求的等差子序列.

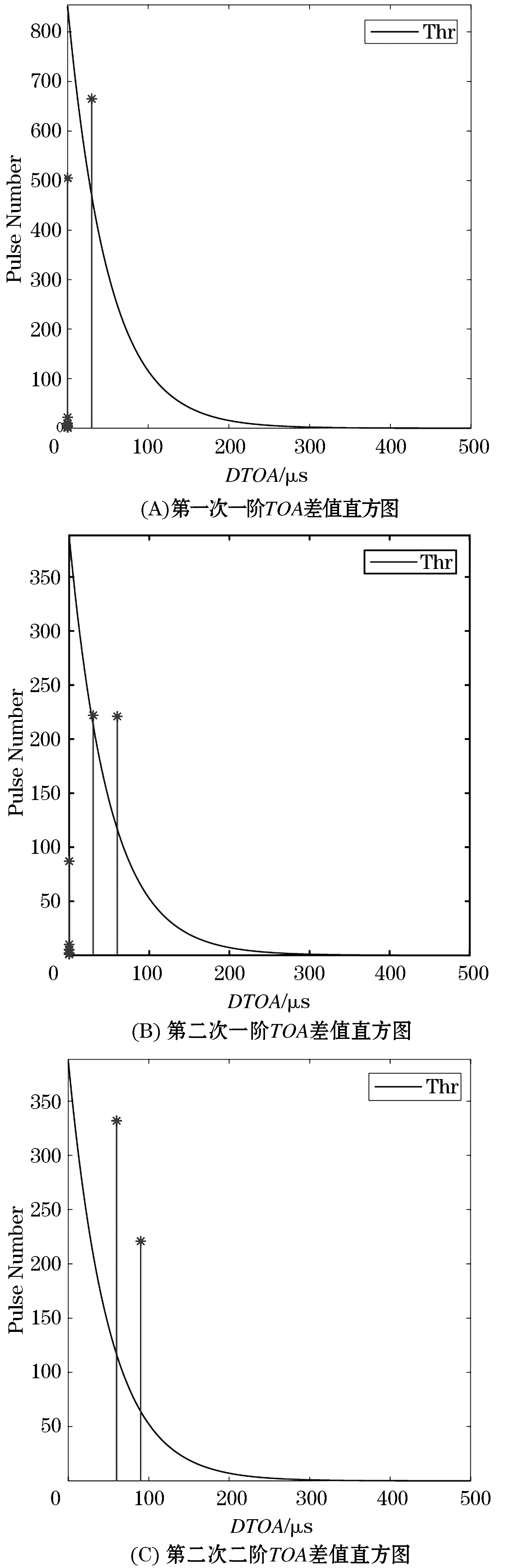
图6 场景2TOA差值直方图统计图

因为有两个峰值超过了检测门限，所以将进行二阶TOA差值直方图统计.其结果图为图6(C)所示.由图6(C)可知在第二次二阶TOA差值中方图中有两处峰值都过了检测门限，其对应的TOA差值为60、90 μs,对这两个潜在PRI进行序列搜索，都能成功分选处对应的固定PRI雷达.因此对于场景2利用改进SDIF算法的分选结果如表3所示.

表3 场景2中改进的SDIF算法分选结果

从表3可以看出在场景2中改进的SDIF分选结果完全正确.因此引入的等差鉴别流程并不会影响传统SDIF原本适用的场景.

场景3的TOA差值直方图统计结果如图7所示.

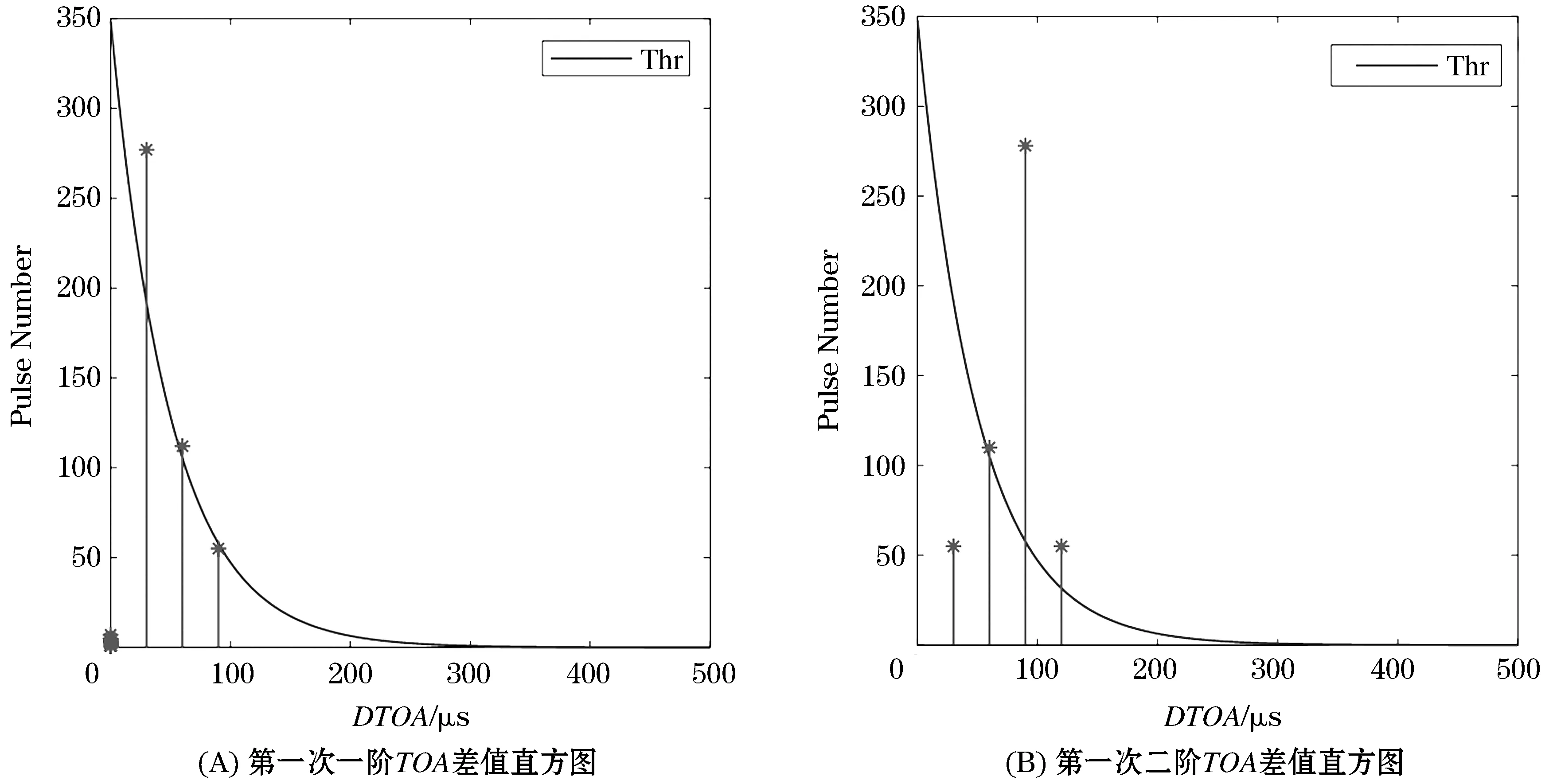
图7 场景3TOA差值直方图统计图

传统SDIF分选：

由图7(A)可知，一阶TOA差值存在多个超过检测门限的峰值，故不会进行序列搜索，而是继续进行下一阶TOA差值直方图统计.在图7(B)中TOA差值等于60、90、120 μs处出现了过门限的峰值.将对这个3个潜在PRI进行序列搜索，以60 μs为间隔不能成功搜索到序列.以90 μs为间隔的序列搜索示意图如图8(A)所示.

由图8(A)可知，可以成功分选出一部90 μs的固定PRI雷达.将该固定PRI雷达的脉冲序列提出出来后，对剩余的脉冲序列以120 μs为间隔进行序列搜索，序列搜索示意图如图8(B)所示.由图8(B)可知，可以成功分选出一部120 μs的固定PRI雷达.在提取完120 μs的固定PRI雷达脉冲序列之后最后剩下的脉冲序列如图8(C)所示，PRI为180 μs的固定PRI雷达脉冲序列.

改进的SDIF算法：

由图7(A)可知在场景3第一次TOA差值直方图统计中峰值处对应的非零DTOA为30、60、90 μs，存在满足条件的等差子序列: 30、60、90 μs.将子序列作为潜在3参差PRI雷达，其骨架周期为180 μs，以180 μs为间隔进行序列搜索，搜索示意图如图9(A)所示.

由图9(A)可知，以180 μs为间隔能够成功搜索到脉冲序列.因此子PRI为30、60、90 μs的3参差雷达在输入脉冲序列中真实存在.将该参差雷达对应的脉冲序列提取出来之后，剩余脉冲如图9(B)所示.

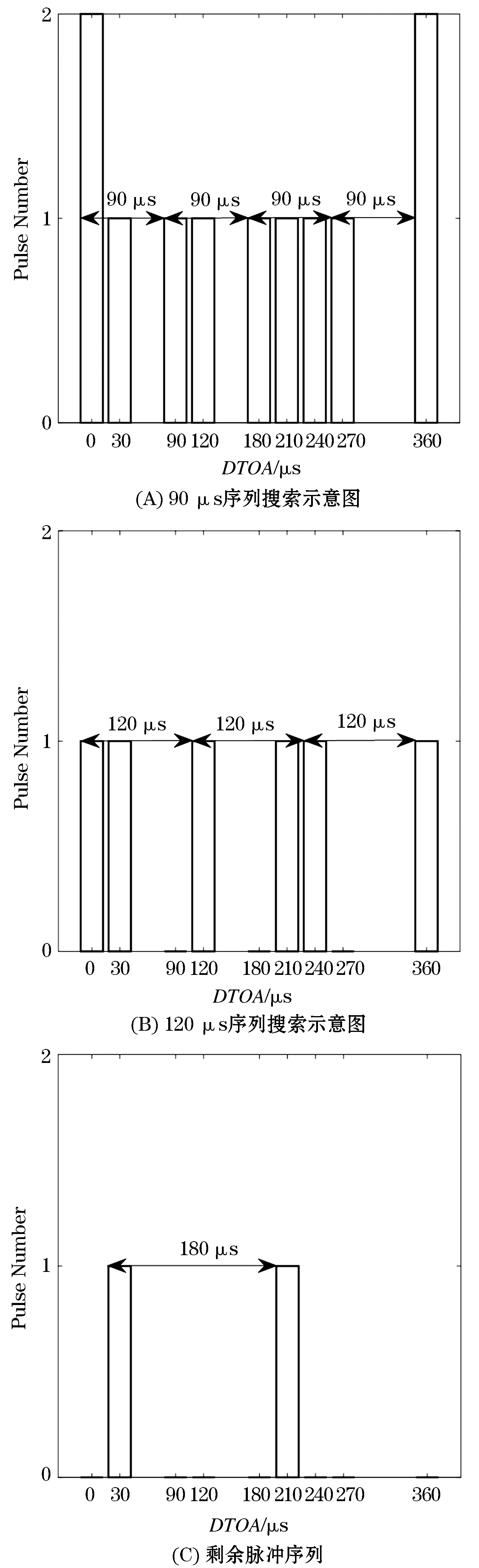
图8 场景3传统SDIF序列搜索

由图9(B)可知，将3参差PRI雷达脉冲序列提出来之后，最后还剩下一部PRI为120 μs固定PRI雷达.场景3中传统SDIF分选算法结果和改进后的SDIF算法分选结果如表4所示.

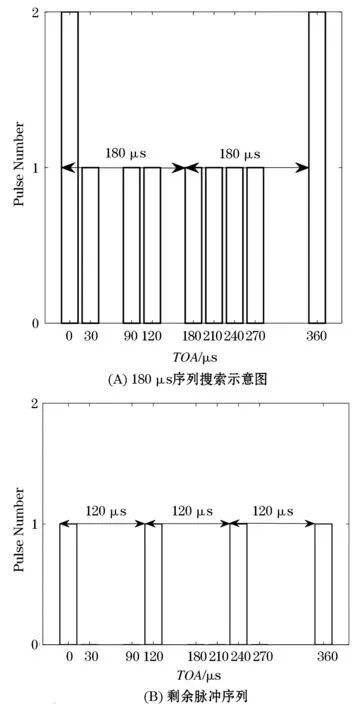
图9 场景3改进SDIF序列搜索示意图

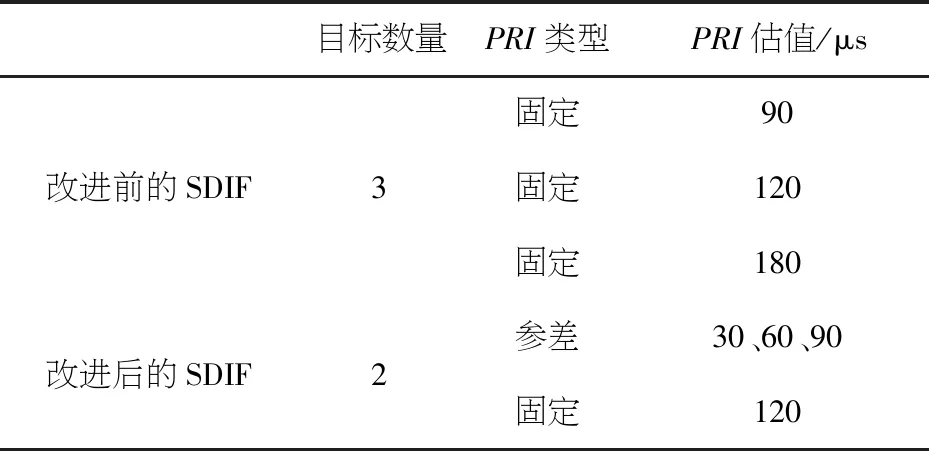
表4 场景3中改进前后雷达信号分选结果比较

从表4可以看出，在场景3中，改进前的SDIF算法分选结果不仅出现了增批现象，而且目标的PRI类型和PRI参数都出现了错误.而改进后的SDIF算法分选结果完全正确.

5 结 语

本文针对基于PRI参差等差设计原理，将等差鉴别引入传统的SDIF算法中，提出了一种基于PRI等差鉴别的改进的SDIF信号分选算法，该算法有效解决了SDIF不能正确分选子PRI为等差序列的参差雷达的问题.仿真结果表明，该算法进一步提升SDIF算法的分选结果的正确性，丰富了其适用场景.且计算量较小，能够应用于雷达电子侦察和电子对抗等实际工程之中.