矩阵分解在典型相关分析与线性判别法中的应用
张子明,徐常青
(苏州科技大学 数理学院,江苏 苏州215009)
大数据是当前研究的热门学科之一,它涉及信息科学、统计学、计算数学、计算机科学和数值分析等,属交叉性应用领域[1]。尽管到目前为止大数据还没有一个统一的数学化定义,但通常人们把大数据理解为比传统数据更复杂、维数更高且具有量(Volume)大(可达10 个Tb 以上)、更新快(velocity)、类型多(variety)三个特征(称为3V)[2]。数据分析中著名的维数魔咒(The curse of dimensions)问题[3]描述当样本点对应的特征向量(feature vector) 维数达一定程度后,相应变量或不变量的计算量(如样本点集合对应的主成分的计算)将呈指数增长。这类问题在计算机网络、张量分解(如张量CP 分解[4])和模式识别等学科和理论中普遍存在,因此,降维问题是大数据和传统数据分析面临的一个关键问题[5]。
高维数据集对应一个高维样本集,而数据分析的最终目的是对样本分类并建立样本分类预测模型。高维数据不仅难以被人们直观理解,也难以被现有的机器学习和数据挖掘算法有效处理,因而很难建立样本分类预测模型,比如LDA 算法在高维数据中往往性能不佳[6]。另一方面,低维统计度量在许多统计问题中有着重要的作用,如数据的统计分析和数据特征可视化等[7]。寻找一个从高维空间到低维空间的一个具有某种理想属性的映射以实现数据降维是挖掘高维数据中有效信息的必要步骤[8]。
线性子空间学习(Linear Subspace Learning,简称LSL)方法尝试寻找这样一类线性映射,它将高维数据集合中的样本点投影至一个低维线性空间,以实现数据的降维[9]。该映射是通过对一个目标函数的最优化来学习产生。线性子空间学习基本方法包括主成分分析法(Principal Component Analysis,简称PCA)、线性判别分析法(Linear Discriminant Analysis,简称LDA )、典型相关分析法(Canonical Correlation Analysis,简称CCA)和偏 最 小 二 乘 法(Partial Least Square Method,简 称PLS)等[10]。LDA 在 自 然 语 言 处 理(Natural Language Process,简称NLP)和人脸识别等模式识别中有广泛应用。LDA 在类别信息(或部分)已知的前提下通过一个线性投影以实现数据降维。因此,LDA 也是一种经典的有监督或部分监督条件下的降维方法[11]。CCA 通过两组变量中部分变元的线性组合以生成低维综合指标向量组,来代替原始样本点集合,以考察两组样本集合之间的相关性[12]。CCA 在研究宏观经济走势与股票市场走势之间的关系、病人医疗费用与医疗保险支付的关系等众多问题中有广泛应用[13]。
给定数据集M={x1,x2,…,xN},其中每个数据点xm∈RI为一个向量,S 为V=RI的一个线性子空间,且满足0 记E=[β1,β2,…,βP]∈RI×P,则rank(E)=p,令U=E(ETE)-1ET,则U∈RI×I为一个对称幂等矩阵,故为一个投影矩阵,且∀x∈RI,Ux=E(ETE)-1ETx=Ey∈S,其中y=(ETE)-1ETx∈RP。 从以上分析可以看出,在给定目标投影子空间(或它的一组基)的前提下,理论上可计算出相应的线性投影映射,从而实现数据降维。因此,寻找投影线性子空间S 成为线性子空间方法的核心。 在大数据背景下,数据集M 所含数据点的个数及其所在的空间维数I 通常会是几千万甚至是几十亿,这时线性子空间学习需要很大的计算量。笔者将利用矩阵分解和矩阵分析方法对线性子空间方法中的LDA和CCA 方法进行改进,以提高计算效率。 LDA 为样本分类线性学习方法。给定训练样本集M={x1,x2,…,xN}⊂RI,其中每个样本点xm∈RI是一个向量。记样本矩阵为X=[x1,x2,…,xN]∈RI×N。LDA 方法寻求一个线性投影映射σ,使同类样本在σ 下的投影尽可能近,异类样本投影点尽可能远。注意LDA 中的每个训练样本点都有类别标记。 记r 为类别数,C1,C2,…,Cr为类别标记。定义类指示矩阵P=(Pij)∈RN×r为(0,1)-矩阵且Pij=1 当且仅当xi∈Cj;类标记矩阵D=diag(n1,n2,…,nr),其中ni为类Ci所含样本点个数。样本集的类内散度矩阵和类间散度矩阵分别定义为 其中μi是样本集Ci的样本均值。可以证明: 引理1 (1)类指示矩阵P的列向量构成正交向量组,且有PTP=D。 (2)令W=IN-PD-1PT,则W为投影矩阵,且Sw=XWXT。 (3)令R=Ir-(1/r)eeT(e为r 维全1 向量),B=PD-1/2RD-1/2PT,则R和B为投影矩阵,且Sb=XBXT。 证明(1)设pi与pj分别是矩阵P的第i 列与第j 列,由矩阵P的定义易知piTpj=0,piTpi=ni,故PTP=D。 (2)由于XP=[μ1,μ2,…,μr]D=μD,所以μ=XPD-1,故有 其中W=IN-PD-1PT。不难证明W为对称幂等矩阵,故W是投影矩阵。 (3)通过直接计算可以验证R是对称幂等矩阵,故R为正交投影矩阵。同时注意到故由(2)式可得 注意到B为对称矩阵,且 故B为对称投影阵。 LDA 的思路是求一个投影矩阵U∈RI×(r-1),使投影后的样本点集合的各类中心到全局中心的距离之和最大,同时各类样本点到其类中心距离之和尽可能小,这里的距离可以是任意类型的距离,一般默认这里的距离为欧式距离。这等价于优化问题 利用Lagrange 乘子法不难发现,(3)式等价于广义特征值问题 结合引理1,注意到P 为0-1 矩阵,D 为对角阵,因此,广义特征问题(4)的计算量会大幅减少。 CCA 是分别对两组数据进行线性投影,通过综合变量之间的相关性来反应两组指标之间的相关性。它在研究国民经济与多维有监督学习中有广泛应用[14]。 设有两组数据集X∈RI×N,Y∈RJ×N,N 是每组的样本个数,I 与J 是每组数据维数。记X,Y 对应的样本协方差矩阵(又称样本散度矩阵)分别为Σxx,Σyy,即 若记H=IN-JN(JN=eeT),则有 同理 定义两变量p,q 的Pearson 相关系数为 下面是传统的CCA 方法中逐次计算投影向量对的方法和步骤: (1)第一对投影向量:设ux1∈RI和uy1∈RJ分别是两组数据的第一对投影向量。目标函数为 优化问题(9)等价于 写成拉格朗日乘子法形式为 其中λ 和μ 是拉格朗日乘子。于是有 由式(13),得到 由式(14),得到 将式(16)代入到式(13),式(15)代入到式(12),得到 变成了求矩阵特征值与特征向量问题。(假设Σxx与Σyy均可逆)。 (2)第P 对投影向量:与求第一对投影向量类似,只是目标函数多了如下几个限制条件[15],即为减少数据冗余度,希望投影后的每组数据特征不相关且与两组间不配对特征无关。 其中q=1,2,…,p-1。这样可找到p=min{I,J}对投影向量{u˜xp,u˜yp}(详细推导过程见文献[15]),组成投影矩阵为其中 总结上述得到如下算法: 输入: 训练集X={x1,x2,…,xN},Y={y1,y2,…,yN};xm∈RI,ym∈RI; 过程: 1:根据式(5)、(6)、(7)分别计算Σxx、Σyy、Σxy; 2:通过逐个解式(16)和(17)这样广义特征值问题得到p 对{uxp,uyp},其中p=min{I,J},p 对{uxp,uyp}这样投影向量组成投影矩阵 传统的CCA 方法需要多次迭代以逐次计算投影向量对并最终生成投影矩阵,这种方法显然非常繁琐,在大数据情形下没有可行性。下面用用更简洁的矩阵形式计算投影矩阵,避免了繁琐的迭代过程。 其中Λλ=diag(λ1,λ2,…,λI)。则 定理1设Σ=cov(x,y)为协方差矩阵,其中x,y∈RI。Σxx、Σyy、Σxy、Σyx为2.1 中定义的样本协方差矩阵,令则存在正交矩阵W∈RI×I,使 证明 注意到 所以W 是正交矩阵。证毕。 由定理1,可得到如下算法: 输入: X={x1,x2,…,xN},Y={y1,y2,…,yN};xm∈RI,ym∈RI; 过程: 1:根据式(5)、(6)、(7)分别计算Σxx、Σyy、Σxy; 文中对线性判别法(LDA)与典型相关分析法(CCA)通过矩阵分解的形式进行了改进。在LDA 中,类内散度矩阵Sw=XWXT,类间散度矩阵Sb=XBXT,较(2)式形式更简洁且计算量更小。接下来问题是如果对(3)式可以进一步化简,那么LDA 效率将会进一步提高。对于CCA,如果两组数据集维度相等(如果两组数据集维度不相等,可以尝试对其进行降维处理使其相等),那么目标投影矩阵可以直接利用矩阵乘法求出,更易于编程且大幅节省计算时间。 事实上,LDA 与CCA 可以推广到张量,比如利用张量CP 分解等张量知识进行处理,有关内容读者可参阅文献[15]。
1 线性判别法的改进
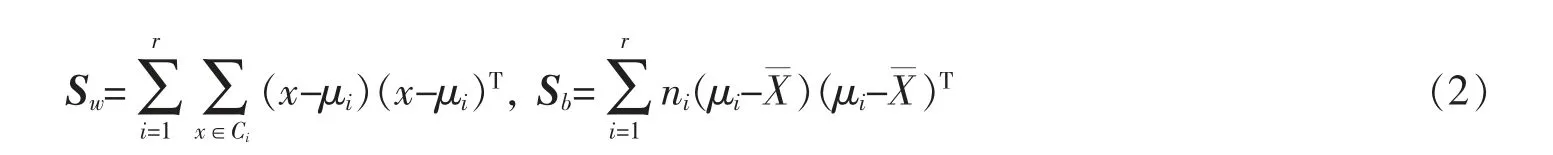
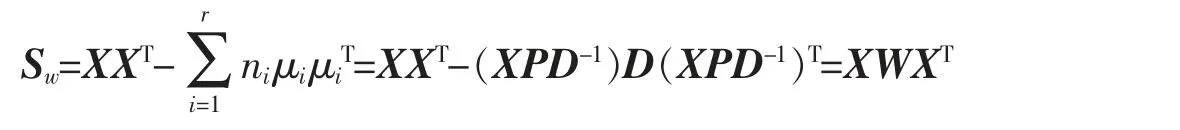
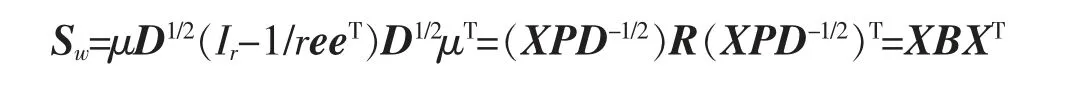
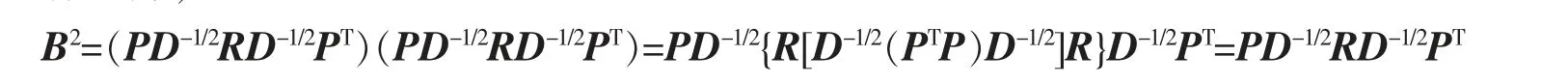


2 典型相关分析法的改进
2.1 迭代方法推导典型相关分析


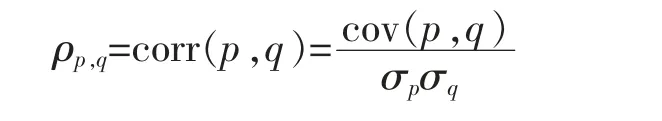
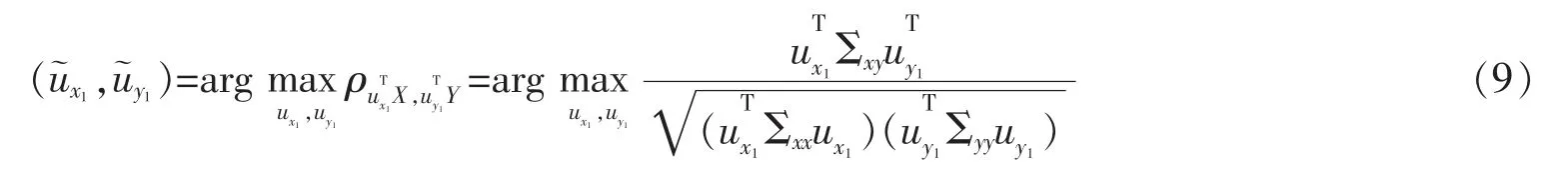

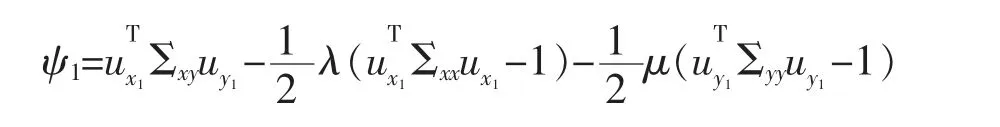






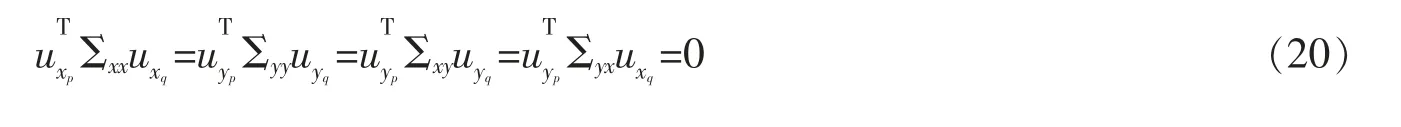
2.2 典型相关分析的矩阵推导形式
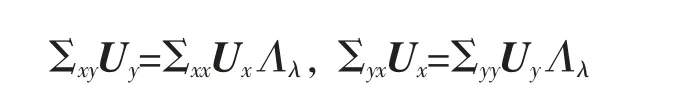
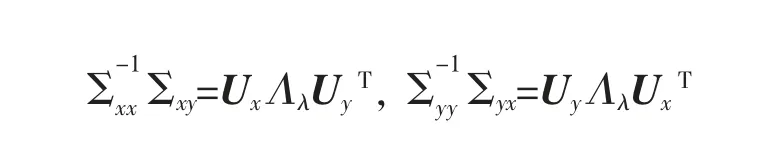
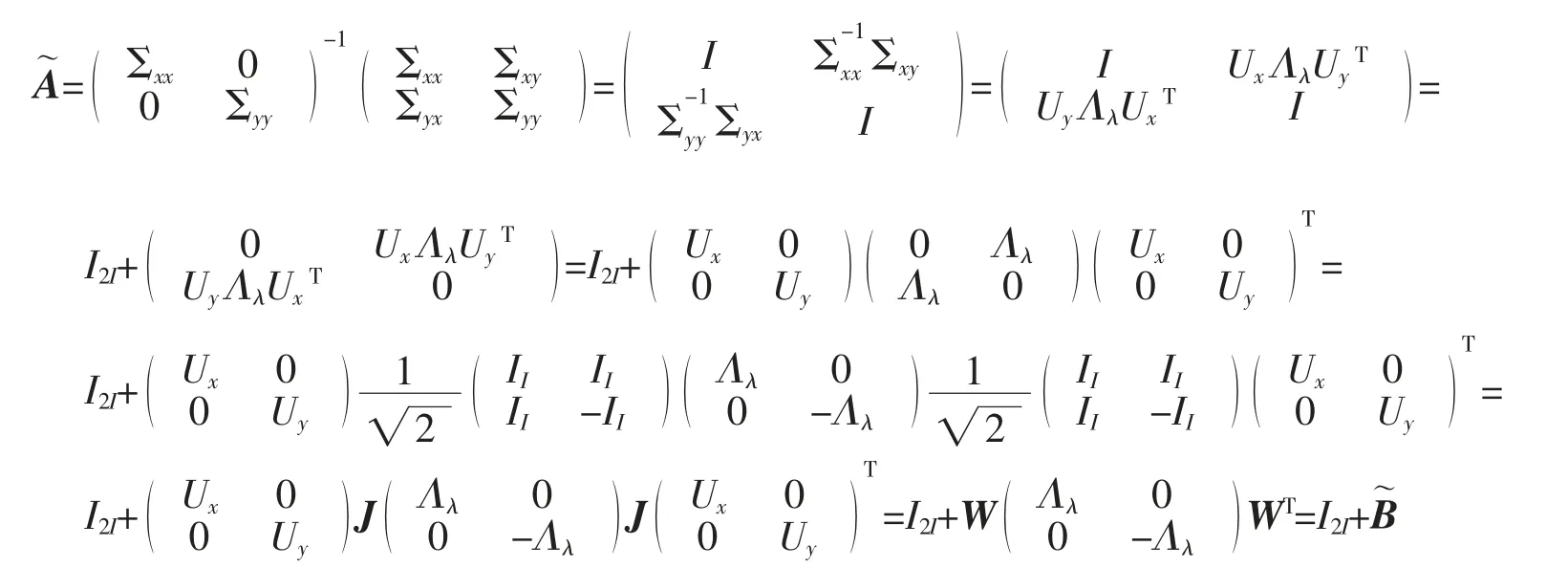
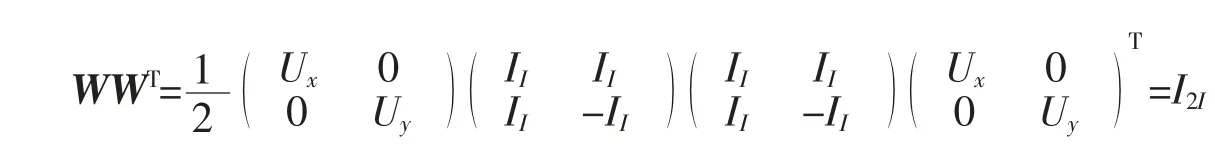
3 结语

