基于相对熵的开放系统量子参数估计

杨志远，严 凯，邵雅婷，郝 翔

（苏州科技大学 数理学院，江苏 苏州215009；江苏省维纳热流技术与能源应用重点实验室，江苏 苏州215009）

信息度量是信息论[1]中最基本的问题之一。经典信息论中，最早在数学上定义的“信息”是Fisher 信息，它被广泛的运用在数理统计和参数估计问题[2-5]。从物理角度看，可以采用“熵”来度量信息，信息熵是表示事件不确定性的度量。经典信息熵和经典Fisher 信息可以通过Kullback-Leibler（KL）距离[6-7]建立联系。KL 距离是数学统计中一种非常重要的量，可以用来评价某种参量分布的离散特性，与信息熵紧密相连，被广泛应用于测量领域。在量子测量领域中，量子KL 距离对应相对熵。在文献[8]中，Wiener 提出Fisher 信息可以被信息熵取代。然而，在量子力学中，Fisher 信息扮演着重要的角色[9－11]，通过Fisher 信息可以导出其他形式的信息量。在此，笔者推导出相对熵和量子Fisher 信息的关系，通过比较两个含有参数的邻近态的距离，提出一个用于开放量子系统参数测量的有效定性判据。

文章主要内容分为三个部分：首先，利用量子态KL 距离导出了一个可以衡量量子态含有测量参数的量子信息散度；然后，利用两种判据，研究了两能级系统在三种噪声通道中的退相干过程；最后，给出一个简要的总结。

1 基于邻近态距离的参数估计判据

首先，一个经典态X 可以用一个概率分布函数{px}表示，满足它和另外一个经典态qx之间的差异可以用两个经典态的距离表示。一个是经典态Bures 距离其中fc(px，qx)=为保真度[12]。另一个是，经典态KL 距离也可以有效表示近邻经典态的距离。其中，Bures 距离度量是严格的数学度量，而KL 距离却不是度量，因为既满足对称条件：也不满足三角形不等式[9]。

设经典的概率分布px含有未知的参数θ。当参数θ 发生微小变化Δθ→0 时，两个近邻态的距离可以用上述两种距离度量表示成[6]

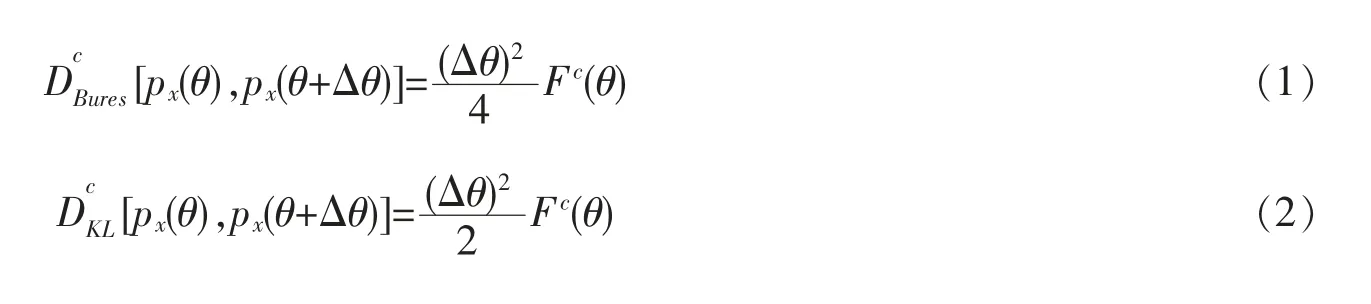
下面给出公式（1）和（2）的简单推导过程：将离散概率分布px(θ+Δθ)在θ 处泰勒展开并保留至二阶项，根据两个邻近经典态的保真度，得到

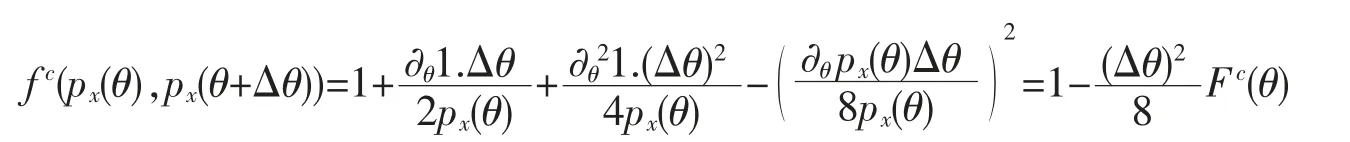
从而得到公式（1）。

同样，根据KL 距离公式定义，只保留2 阶项，可以得到公式（2）

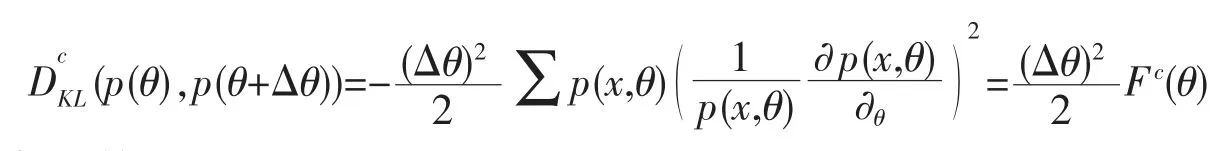
对于多参数也有相类似的结论[7，13-14]。

然后，将经典态距离的结论推广到量子态问题。一个量子态可以由一个密度算子ρ 表示，可以看成是概率密度函数px在量子论中的推广[15]，满足Tr[ρ]=1。如果ρ为对角矩阵，则量子态可以退化到经典态px。上述经典态的距离度量，都可以推广到量子情形。两个量子态ρ，ɐ 的Bures 距离量子保真度定义为量子KL 距离[16]定义为DKL(ρ||ɐ)=Tr[ρ(log ρ-logɐ)]。量子Fisher 信息也可以通过参数估计得到，对于无偏参数估计，参数θ 估计的误差下界由量子Fisher 信息F(θ)[17-18]表示，F(θ)=Tr(∂θρL)=Tr(ρL2)，L 对称对数导数算子满足条件2∂ρ=ρL+Lρ，其中例如，关于纯态｜ψ〉中θ 参数估计，其量子Fisher 信息量为对于混合态可以写成[19]

将F(θ)进一步展开写成经典贡献项Fct和量子贡献项Fqt[20]，F(θ)=Fct+Fqt，其中

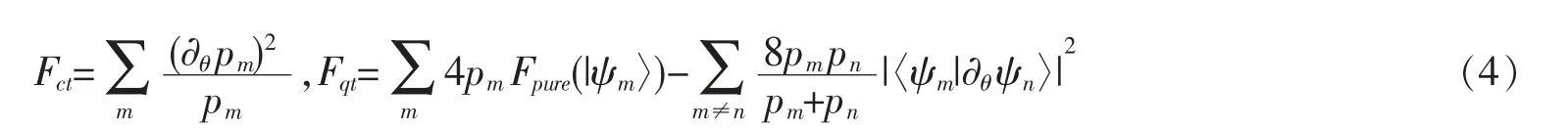
同样，考虑量子KL 距离区分两个邻近量子态。当log(θ+Δθ)在θ 处泰勒展开，保留2 阶项，化简得到，

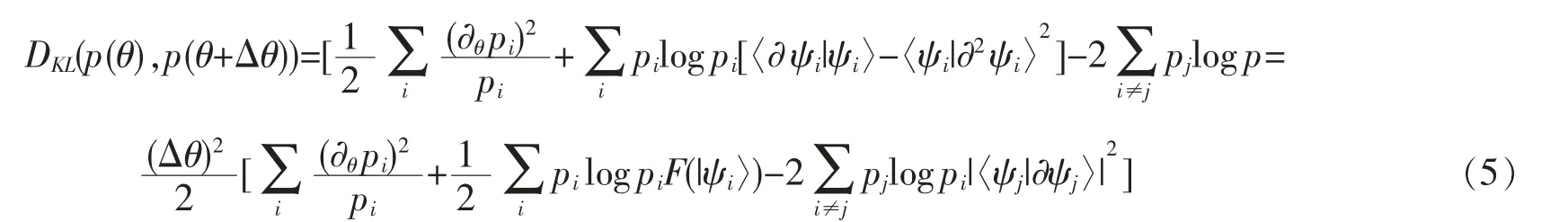
类比Bures 邻近态距离与量子Fisher 信息量的关系，可以定义量子信息散度

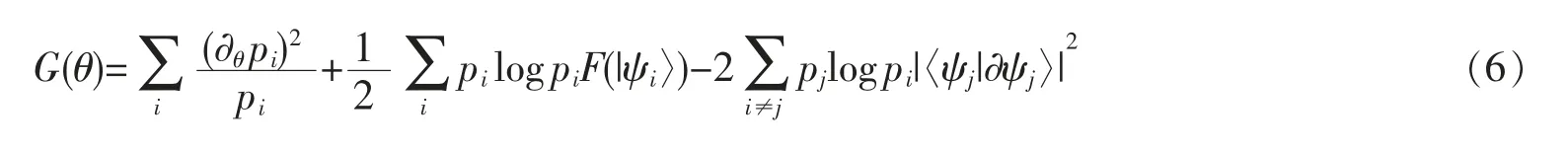
当量子态退化经典态时，量子信息散度G(θ)退化为量子Fisher 信息。规定0log0=0，plog0=-∞，p＞0，对于纯态｜ψ〉，G(θ)=∞。对于完全混合态p1=p2=…=pd=1/d，G(θ)＝0。与量子Fisher 信息量相比，量子信息散度是一种定性的参数测量判据。但是，对于开放量子系统参数估计，量子信息散度可以明显地表现环境噪声对量子参数估计的影响，可以看做量子Fisher 信息量的一种有效补充。

对于封闭系统，以两能级系统ρ2×2=p1｜ψ1〉〈ψ1｜+p2｜ψ2〉〈ψ2｜为例，G(θ)和F(θ)为

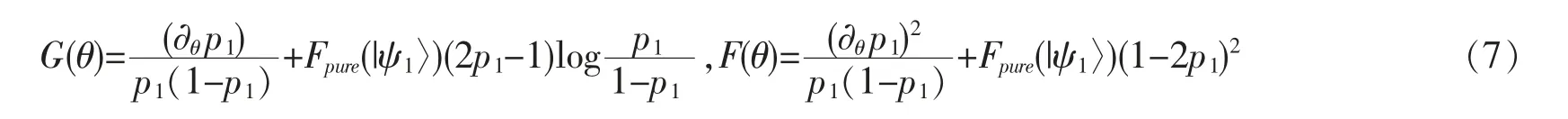
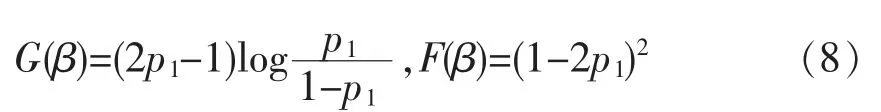
在图1 中，p1=1,0 对应着纯态｜ψ1〉和｜ψ2〉，此时的G(β)和F(β)分别取最大值∞和1。p1=1/2 对应着完全混合态，此时的G(β)和F(β)取最小值0。从图1 中可以看到量子态的纯度Tr(ρ2)与G(β)和F(β)相比，它们变化趋势相似。

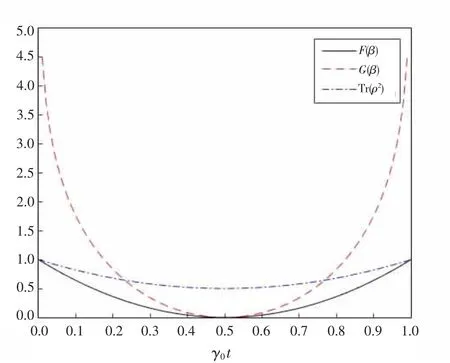
图1 两能级混合态ρ2×2，关于相位参数β 的G(β)和F(β)随p1 的变化图

2 量子噪声通道中G(θ)和F(θ)

在实际情况下，量子系统总会受到环境噪声的影响。这就需要研究开放系统在噪声背景中的量子参数估计。以两能级系统为例，任意纯态分别经历一些量子噪声通道，如退相位通道（PD）、退振幅通道（AD）、退极化通道（D）[17-18]。在上述三种通道中，量子态表示为

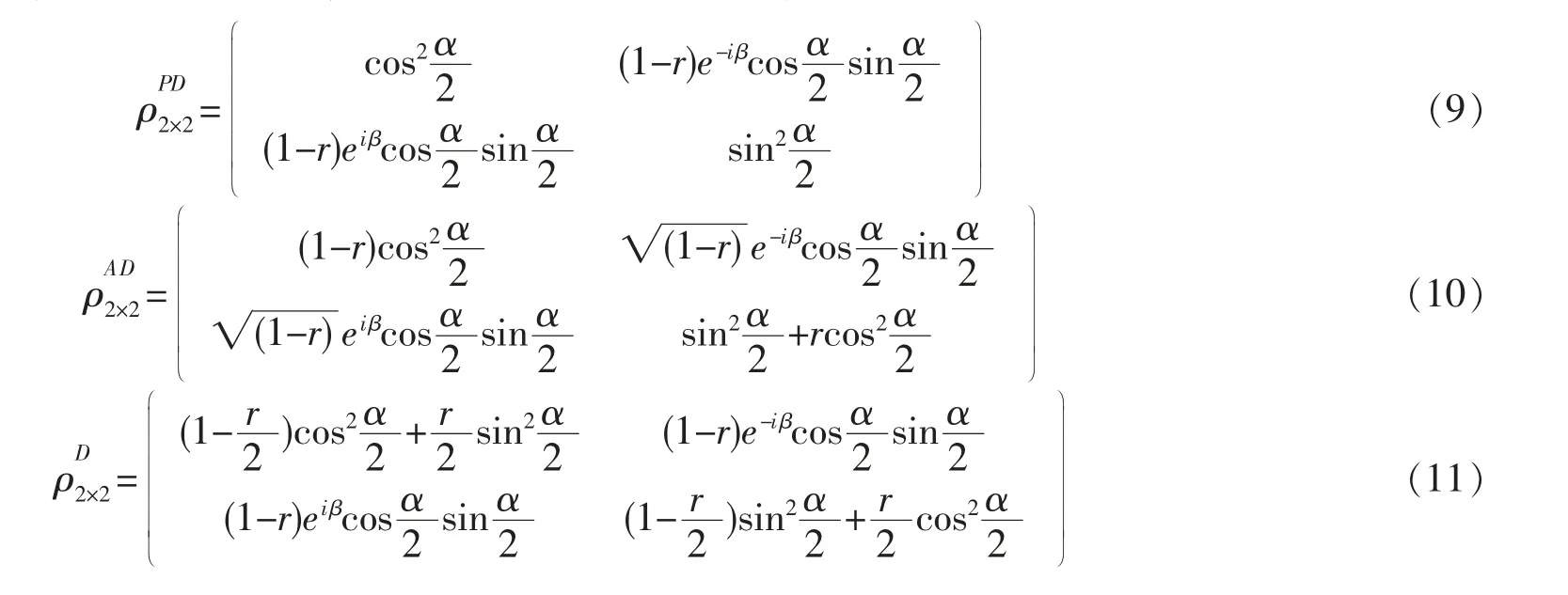
其中r=1-exp(-γ0t)为各个通道中的退化参数，γ0为马尔科夫近似下的耦合常数。

为方便计算，公式（12）和（13）也可以借助Bloch 矢量B 表示[21-22]

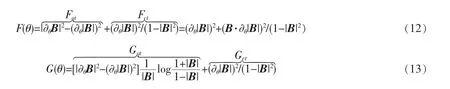
利用Bloch 矢量B=(Bx，By，Bz)，可以把两能级系统的密度矩阵ρ2×2表示为其中σi=x，y，z为Pauli 矩阵的三个分量。

利用公式（12）和（13），可以得到三种通道中对相位参数β 的G(β)和F(β)，以及对权参数α 的G(α)和F(α)。下面对这三种通道分别讨论：

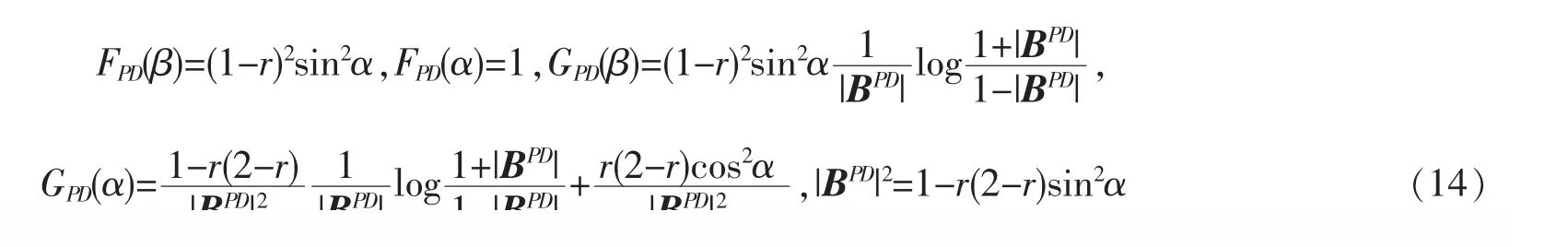
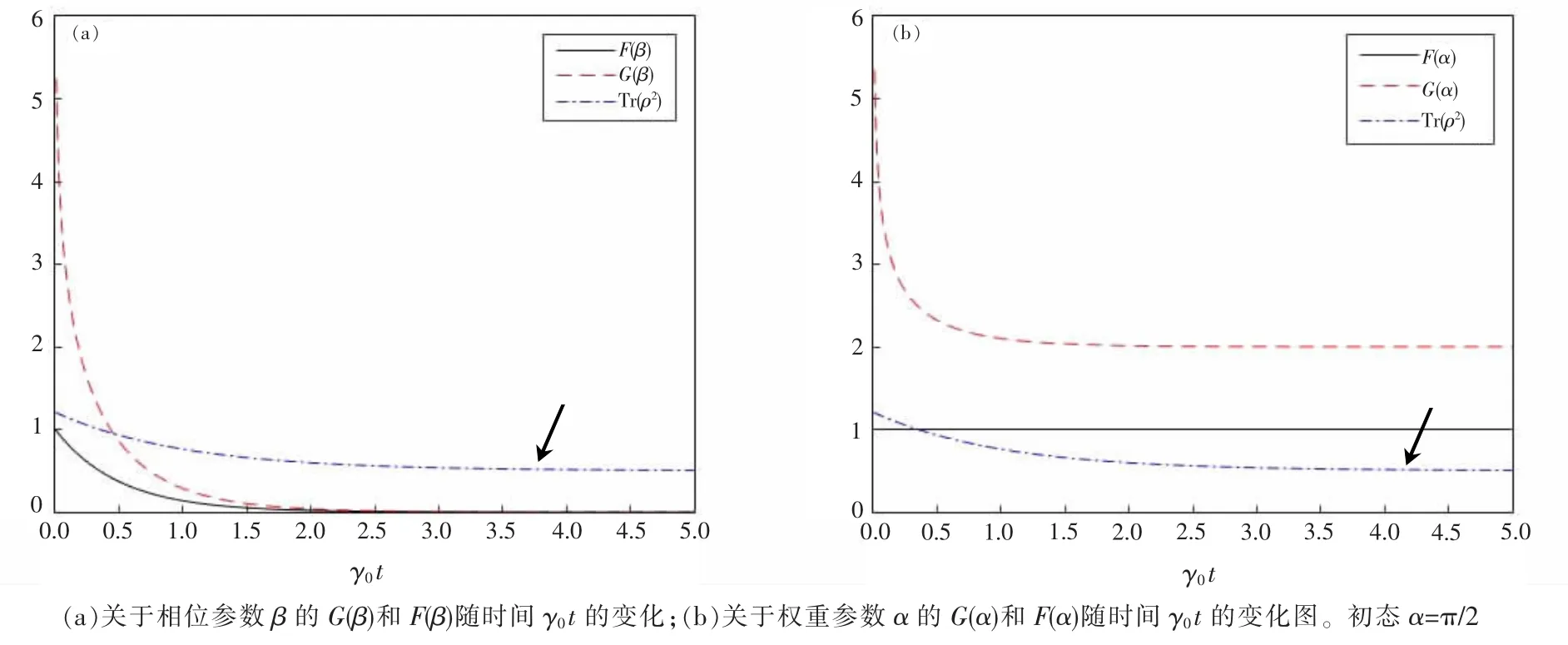
图2 退相位通道中，初态

图2 中绘制了退相位通道中G(α)和F(α)，以及G(β)和F(β)随时间的衰减图像，箭头所指曲线即为Tr(ρ2)随时间的变化曲线。可以发现G(β)和F(β)都随时间衰减，ρ 由纯态向混合态变化，F(β)由sin2α 衰减到0，G(β)由∞衰减到0。而对权重参数α，量子Fisher 信息量保持为1 不变，实际表示的是量子态

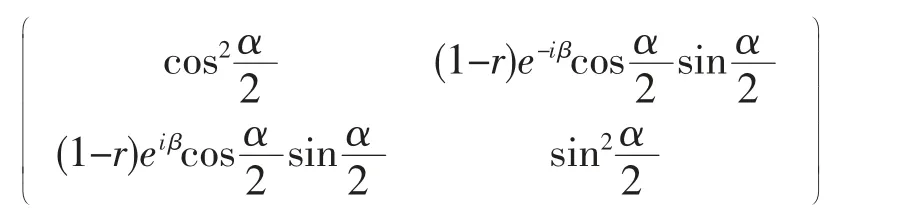
的最优测量是对基矢｜0〉和｜1〉的测量{M0=｜0〉〈0｜,M1=｜1〉〈1｜}，此测量对应的Fisher信息为而G(α)是由∞向1 衰减的，∞对应着纯态，1 对应着经典态此时G(α)就为经典态的Fisher 信息F(α)=1。

（2）退振幅通道

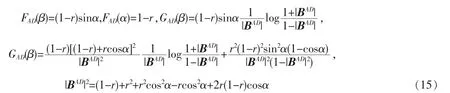
图3 为退振幅通道中G(β)和F(β)，以及G(α)和F(α)随时间的衰减图像。在退极化通道中，对相位参数β，F(β)从最大值(1-r)sinα 衰减到0，G(β)从∞衰减到0。对权重参数α，F(α)从(1-r)衰减到0，G(α)从∞衰减到0。

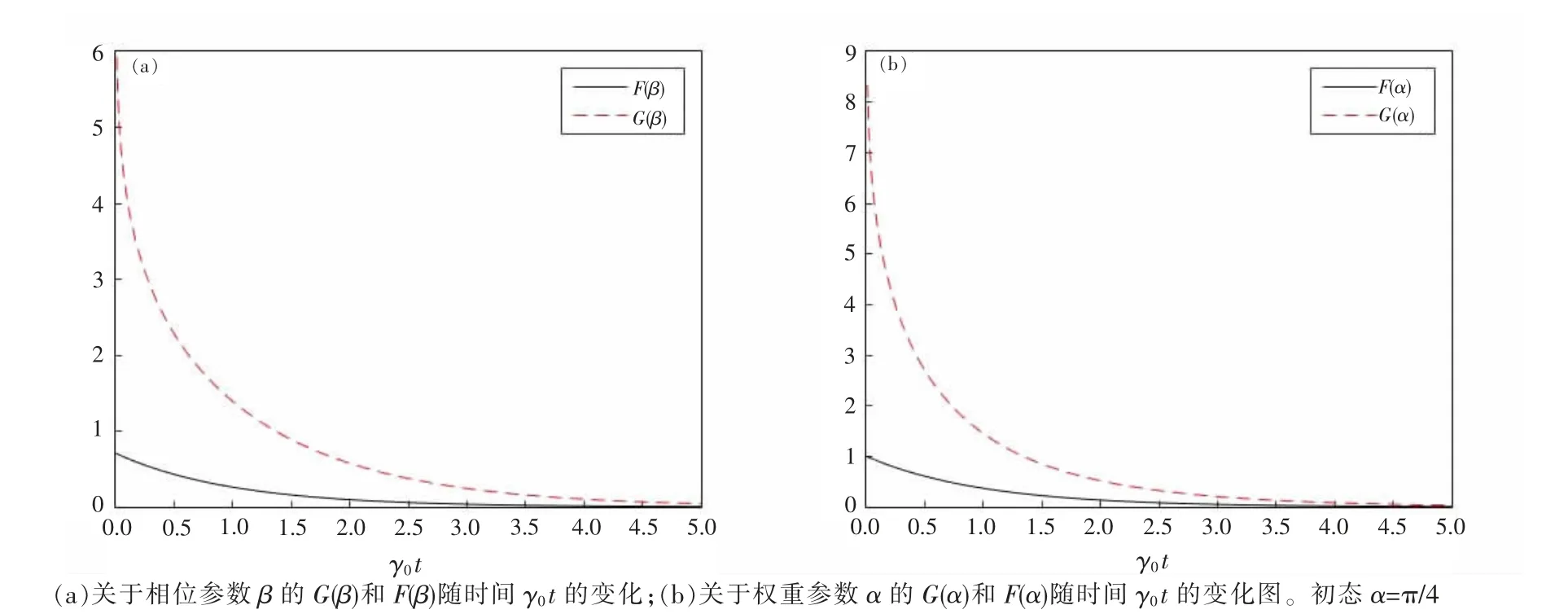
图3 退振幅通道中，初态

（3）退极化通道

退极化通道中：F(β)=sin2α，F(α)=(1-r)2sin2α，G(β)=sin2(α)，G(α)=(1-r)sin2αlog（2-r）/r，图4 中绘制了它们随时间的变化曲线。

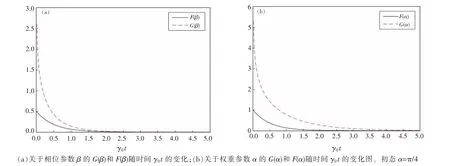
图4 退极化通道中，初态初态

与量子Fisher 信息F(θ)相比较，G(θ)也能表示量子通道中，量子态含有的参数θ 信息随时间的变化情况。随着量子态与环境相互作用，发生退相干量子态变为经典态（密度算子非对角矩阵元变为0），F(θ)和G(θ)均退化为经典Fisher 信息F(θ)。G(θ)在数值上总是大于F(θ)，在退相干环境中，G(θ)衰减的速度要比F(θ)快。这表明，G(θ)受环境的影响更明显，F(α)在退相位通道中保持1 不变，不受环境影响，而G(α)是由正无穷衰减到1，受环境影响。

3 结语

量子KL 距离和量子信息散度G(θ)的关系可以看成是经典KL 距离和经典Fisher 信息关系在量子态空间中的推广。笔者研究了在不同的退相干过程中G(θ)随时间的变化。发现：在三种量子噪声通道中，G(θ)对于相位参数和权重参数都是单调减少的。G(θ)与F(θ)的变化趋势相似。当参量变化同样数值时，G(θ)比F(θ)降低趋势更快。量子信息散度可以很好地定性表现环境噪声对参数测量的影响，是量子Fisher 信息量的一种有效补充。