基于Laplacian 的稀疏化特征选择方法

吴锦华，万家山，伍 祥

（安徽信息工程学院 计算机与软件工程学院，安徽 芜湖241000）

在机器学习和模式识别领域，传统的学习算法在处理高维数据（如生物特征数据、基因数据、股票交易数据等）时，经常会遭遇到“维数灾难”问题[1]。为解决这一问题，目前主要有两类方法：一类是偏向于高维数据的有效表示，如特征选择、特征提取、稀疏表示等传统数据降维算法；另一类是偏向于构建学习模型，如分类回归模型、聚类模型等，最终的学习模型用于数据的预测和分析。笔者通过提出特征选择方法构建分类回归学习模型，并分析最终的分类性能来检验所提方法的有效性。

近些年来，特征选择方法得到了很多研究人员的关注，旨在从高维数据中提取出有效表示形式，从而为目标学习模型提供帮助。目前特征选择方法主要有Laplacian Score（LS）[2]、递归特征消除法（RFE）[3]、顺序向前移动选择（SFFS）[4]、Fisher Score（FS）[5]、Lasso[6]等，在这些特征选择算法当中，基于稀疏表示的特征选择方法得到了广泛关注和研究，如Lasso 方法模型中，引入的稀疏项保证有价值的特征能被选择，并且Lasso 方法模型同时进行回归分析。然而，该方法在处理高维数据时计算速度比较慢，Tibshirani R 等人[7]在Lasso 方法模型的基础上进行了改进，提出的Fussed Lasso 方法能够对计算速度优化。除此之外，Jie 等人[8]为了解决多模态分类中的问题，利用Lasso 方法模型的稀疏项，并引入正则化项，提出一种基于流形正则化的多任务特征选择方法（M2TFS）。吴锦华等人[9]在Lasso 模型的基础上，引入判别性正则化项，提出新颖的判别性特征选择方法。同样为解决非线性问题，相关研究人员在Lasso 方法的基础上引入核函数并取得不错效果[10]。在实际应用中，Conrad T O F 等人提出一种稀疏蛋白质组分析算法（SPA）[11]用于获取最小判别集，刘宏伟等人[12]将距离特征应用至蛋白质的无序段建模。从上可以看出，现在很多方法模型利用稀疏理论相关知识解决一些问题，然而一个主要缺点是在线性映射过程中忽略了一些有用的样本信息，而最新研究表明，利用数据集的判别上下文和聚集多尺度特征可实现更好的模型分类[13]。

为解决上述问题，并受相关研究工作的启发[8－9，13－15]，文中提出了一种特征选择方法Lap-Spa-Lasso，方法模型中充分保存了样本之间的结构信息，从而帮助选出更具判别能力的特征。具体而言，Lap-Spa-Lasso 方法模型中方法首先包含一个稀疏正则化项，用于保证只有少数具有代表性的特征能被选择。另外引入的Laplacian 正则化项用于保存数据集中同类样本之间的结构信息。进一步，为了提升实验运行速度，采用加速近似梯度（Accelerated Proximal Gradient，APG）[16－18]算法来优化提出的方法模型的求解过程。最后，在8 个数据集上对所提出的方法模型进行实验验证，并对实验结果进行了分析。

论文的组织如下：第一部分简单介绍Lasso 方法模型；第二部分给出所提方法模型及相应的优化算法；第三部分给出实验方法、参数设置和运行环境；第四部分给出了实验结果以及结果数据分析；最后部分对全文进行总结和后续工作的展望。

1 Lasso 方法

Lasso 方法最早是Robert Tibshirani 提出[6]，具体描述如下：

首先，给定训练样本集X＝[x1，x2，…，xN]∈Rd×N，其中xi表示样本中的第i 个特征向量，N 表示样本的数量，d 表示样本特征维数。Y＝[y1，y2，…，yN]∈RN表示类标签向量。在全监督分类问题中，yi表示第i 个样本的类标签，其值可以为离散值或具体数值。在文中，为简单处理，只考虑两类分类问题，因此,yi∈{-1，+1}。而且通常情况下，Lasso 方法优化的目标函数如下

其中w 表示特征向量的回归系数，维数为d。正则项｜｜w｜｜1为L1-范式，用于在高维特征空间中产生稀疏解，如wi为不相关或冗余特征，则wi会被置零，而w 中保留的非零系数表示为样本中有效的特征，可以用于后续的分类。其中，λ 是正则项的参数且大于0，主要用于平衡模型复杂度和数据拟合程度之间的相对贡献，其值通常可通过交叉验证来获取。

2 Lap-Spa-Lasso 方法

在Lasso 及其扩展的相关模型中，一般统一采用线性函数f（x）=xTW=WTx将原始数据从高维映射到一维，但仅仅考虑了样本和对应标签之间的关联，却忽略了样本数据之间的内在关联关系，如同种类型样本，经过投影后可能也会产生比较大的偏差，即将原始数据从高维映射到一维可能会出现很大位置上的偏差；然而在理论上，如果两个样本为同一个类，它们通过映射后应靠更近。为了解决这个问题，在所提方法中引入Laplacian 正则化项

公式中，S=[Sij]为近似矩阵，主要用于刻画样本之间的相似程度，经过简单步骤的数学推导而得到的正则化项。L=D-S为Laplacian 矩阵，D为对角矩阵，其中近似矩阵S可以被定义如下

该项可进行如下描述：如果两个样本xi和xj来自于同类，那么其经过映射后的距离就更小；如果来自于不同类，那么之间的距离就会更大。在某种意义上，公式（2）主要保存通过线性函数映射后同类样本数据之间的特征空间分布信息，而该分布信息可以提高方法模型的分类性能[9，19]。因此，文中提出一种基于Laplacian稀疏化特征选择方法，称为Lap-Spa-Lasso，其目标函数如下

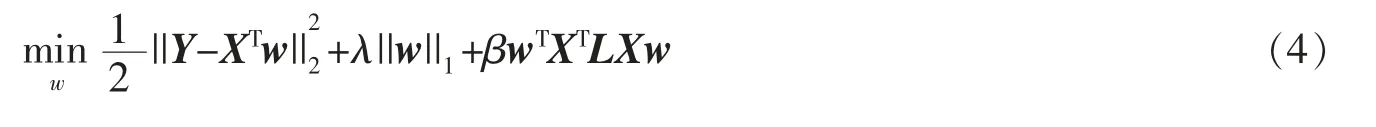
其中λ＞0 和β＞0 为调谐参数，它们的值可以在训练数据的过程中通过交叉验证来确定。两个参数主要用于平衡稀疏项和Laplacian 正则项之间的相对贡献度。

在所提方法模型中，Lasso 稀疏项主要用于选择少量有效特征，而Laplacian 正则化项用于保留同类标签样本之间内在的结构分布信息，从而帮助方法模型选出更具有判别能力的特征集，为后续分类器提供最有效特征。

3 方法求解优化算法

为对方法模型进行求解，文中采用加速近似梯度（Accelerated Proximal Gradient，APG）[16－18]来优化所提出的方法模型。具体而言，首先，目标函数（4）被划分为两部分，即平滑部分

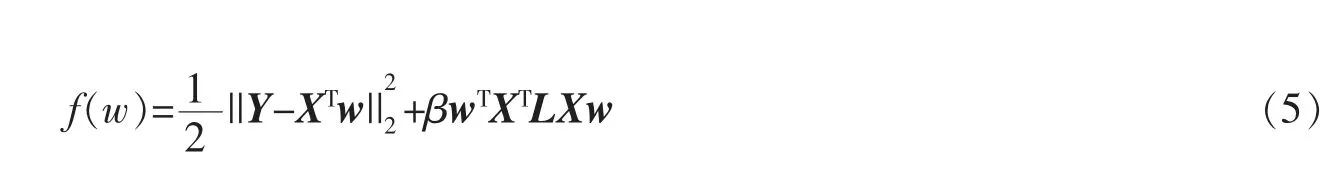
和非平滑部分

记得之前在家时，每隔六个多月，我和母亲就忙着买回一大堆一模一样的衣服。大家都穿一样的东西比较容易分配，可无畏派截然不同。每位无畏者每月都会购置不同的东西，其中当然包括不重样的衣服。我和克里斯蒂娜跑过狭窄的通道，来到文身店。我们到的时候，艾尔已坐在椅子上，一个瘦小窄肩、身上有文身的地方比没文的地方还多的男人正小心翼翼地在他手臂上文蜘蛛。

其次，构造函数Ωl来对f（w）+g（w）公式进行求近似解

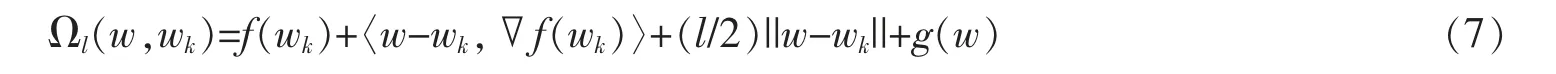
其中，▽f（wk）是第k 次迭代的wk点的梯度，l 是步长，其值可以通过线性搜索的方式来确定。APG 中w 的更新步骤可被定义如下

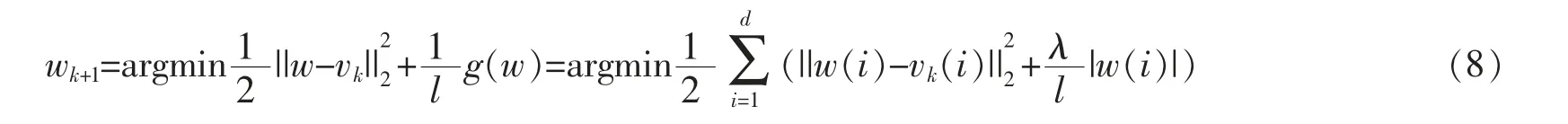
其中vk＝wk－（1/l）▽f（wk）。

因此，根据公式（8），求解优化的问题可以被划分成d 个独立的子问题。APG 算法的关键是如何对这些独立的子问题进行求解。根据文献[16－17]得知，这些子问题的解析解比较容易求取，即

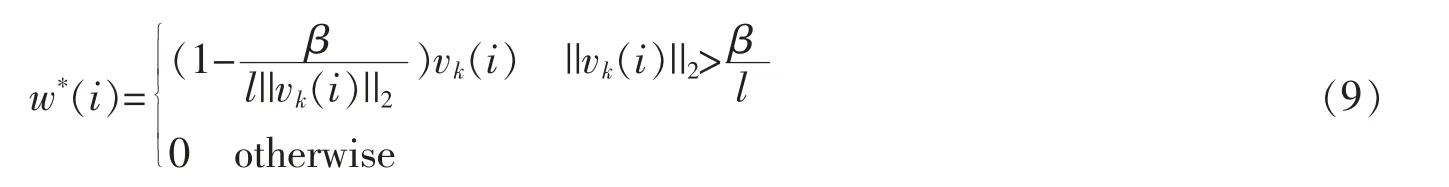
另外，根据文献[17]使用的技巧，文中通过计算如下搜索点来代替在wi上的梯度下降。

以下算法描述总结了APG 算法优化所提方法模型求解过程的细节，其具体过程如下：

输入：令X＝[x1，x2，…，xN]∈Rd×N表示包含有N 个训练样本的数据集，其中d 是样本的特征维数。令Y＝[y1，y2，…，yN]∈RN表示每个样本所对应的类标签，其中每个样本所对应的标签yi∈{-1，+1}。

输出：J*

初始化： β≥0，λ≥0，0≤η≤1，l0＞0，w0＝w1＝0，ρ0＝1

For i＝1 to 最大迭代次数n

1）： 根据公式（10）计算搜索点Qi

2）： l=li-1；

3）： while

f（wi+1）+g（wi+1）＞Ωl（wi+1，Qi），l=σ*l

通过公式（8）计算wi+1

4）： li=l

End 计算J*={j|wj≠0}

4 实验及结果分析

4.1 实验数据集

文中，实验在6 个标准UCI 数据集上和2 个基因表达式数据上来验证Lap-Spa-Lasso 方法的有效性，表1 中给出了样本数据的特征维数和样本个数。

表1 实验数据集

4.2 实验设置

为了验证所提方法的有效性，实验采用10 折交叉验证法。在实验过程中，将样本均等的划分为10 份，其中9 份用于训练模型，并将其中的1 份用于测试，这个过程重复10 次。最后，将平均分类精度作为结果。在实验过程中，为了验证所提方法的适用性，基于RBF 核支持向量机[19]（SVM）、线性核支持向量机以及KNN核进行分类，并分析其在三种分类器下的性能表现。

4.3 实验结果

为评价提出的方法，首先比较Lasso 的特征选择方法，同时也比较了经典的基于特征排名特征选择方法，包括LS、FS、SFFS 和MMFS_ED[20]方法。表2 中总结了所有方法在8 个数据集上的分类结果。从表2 可以看出，所提方法效果都要优于Lasso 方法，表明提出的Lap-Spa-Lasso 方法诱导出了更具有判别力特征，以完成更好的分类性能，间接验证了引入的正则化项在分类过程中的重要性。另外，在大部分数据上所提出的方法都要优于参与比较的方法，这进一步表明了提出方法的有效性。除此之外，论文在线性核分类器和KNN分类器上验证了所提方法的分类性能，从表3、表4 中可以看出，所提方法都要优于Lasso 方法，且在大多数数据集上都有优于传统的特征选择方法，也说明了所提方法具有很好的推广性。

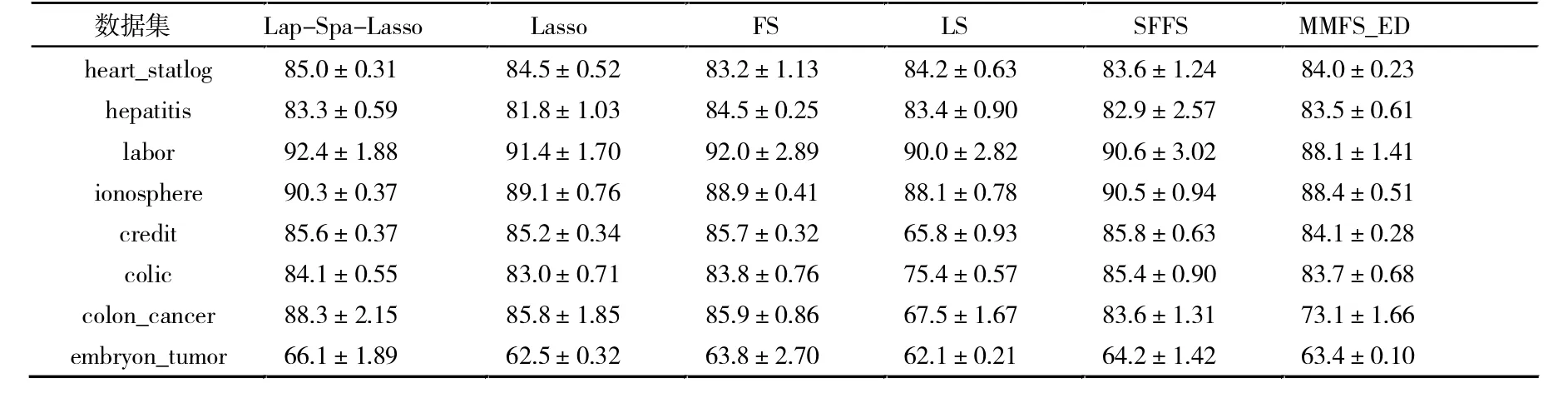
表2 不同特征选择方法在RBF 核上的平均分类精度（±标准差） 单位：%

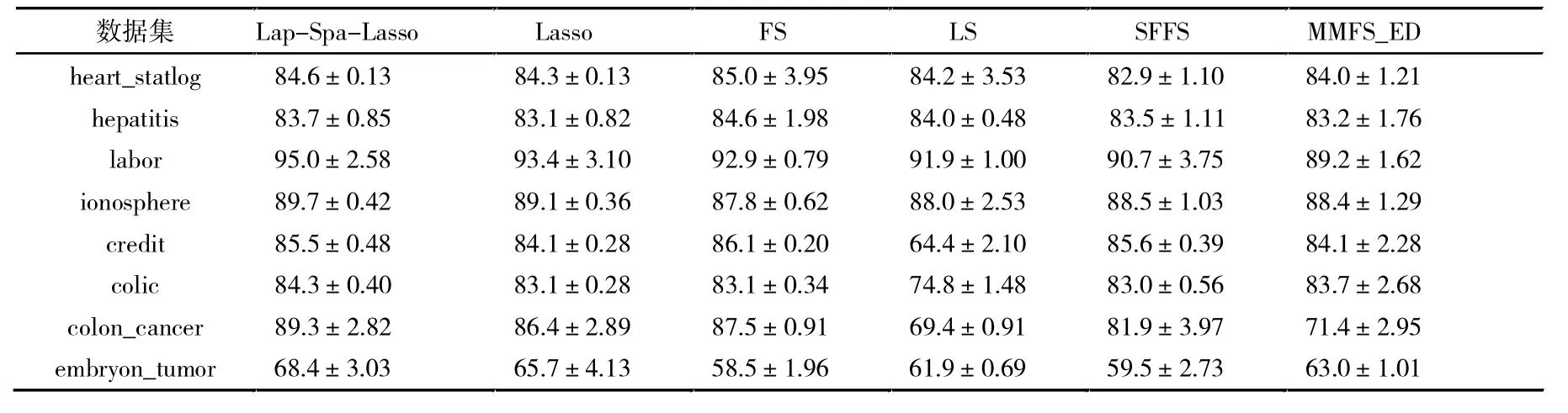
表3 线性核分类器下不同特征选择方法的平均分类精度（±标准差） 单位：%

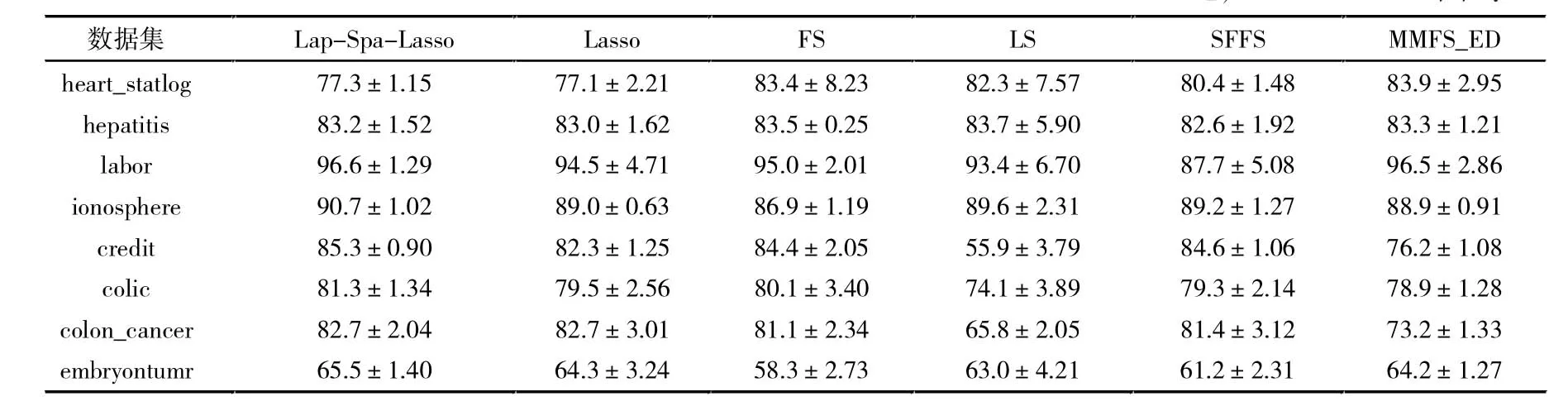
表4 KNN 分类器下不同特征选择方法的平均分类精度（±标准差） 单位：%

文中所提的方法中，当参数β=0 时，方法模型将退化成传统的Lasso 方法。为分析所引入的Laplacian 正则化项的有效性，在8 个数据集上进行实验验证。图1（a）、（b）给出了在数据集ionosphere 和colic 上的实验结果。从图1 中可以看出，所提方法在不同的参数λ 上和不同的数据集上的分类精度都要优于Lasso 方法，除此之外，所提方法所对应的曲线相对Lasso 方法显得更加平稳，即分类性能对参数鲁棒，受参数变化的影响较小。

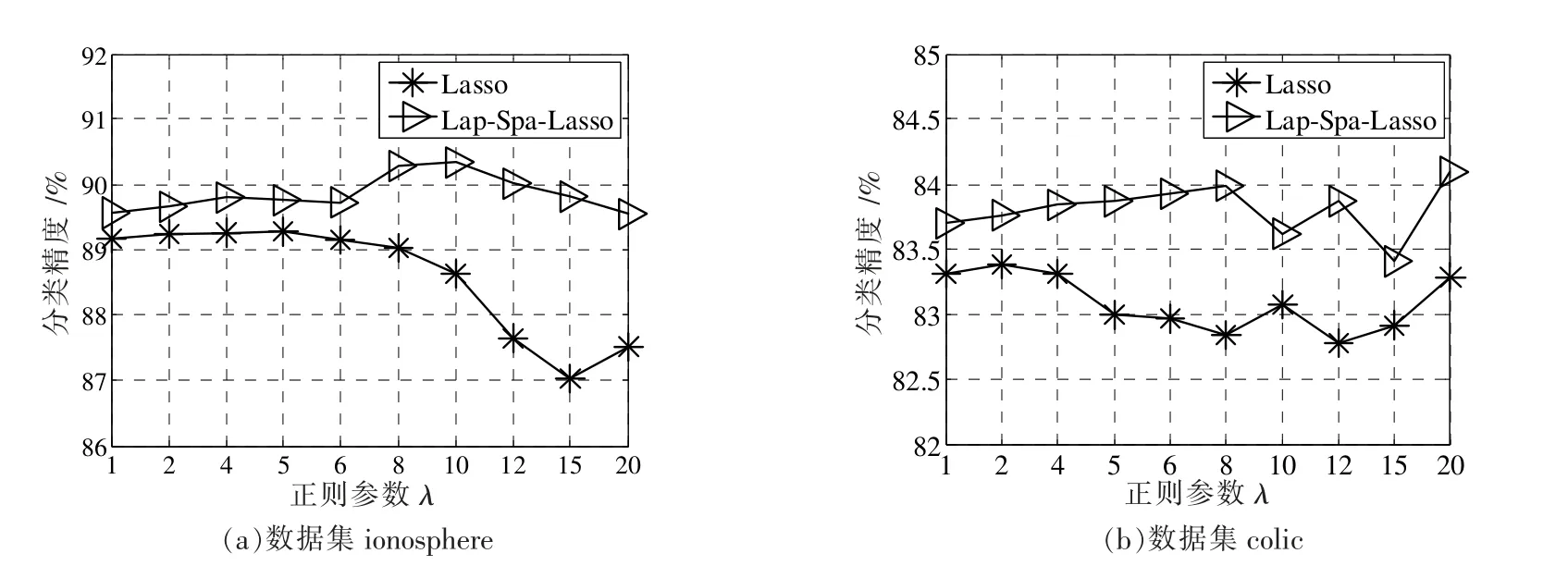
图1 固定β 变化λ 时，所提方法Lap-Spa-Lasso 在2 个数据集上的分类精度

除此之外，分析了固定λ 变化β时提出Lap-Spa-Lasso 方法在8 个数据集上的分类精度。图2 画出了在8个数据集上随不同β 值，所提方法分类精度的变化曲线。由图2 中的曲线分析可见，不同的β 值下所取得的分类结果基本都要好于β=0 时的结果，进一步表明增加Laplacian 正则化项能提升模型性能。除此之外，图2 中绝大数曲线变化趋势都相对比较平稳，说明该模型对参数β 也比较鲁棒。综上所述，所提方法对模型中的参数鲁棒，受参数变化的影响小。

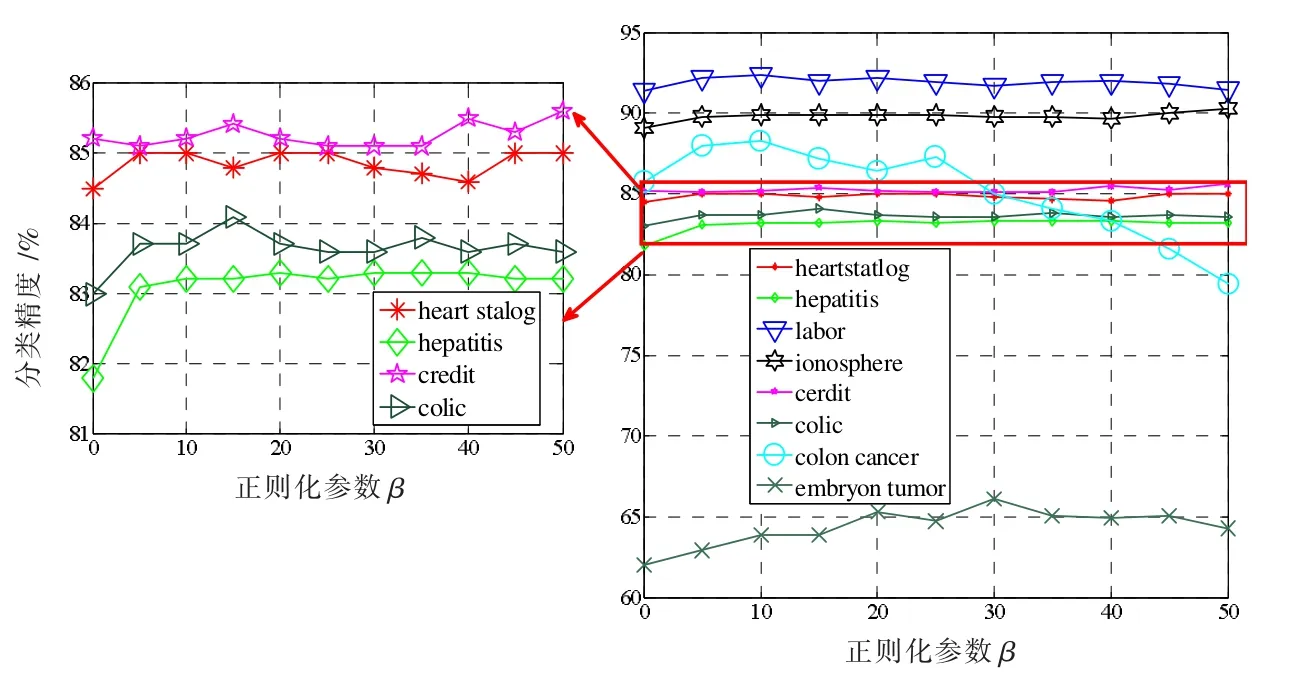
图2 固定λ 变化β 时，所提方法Lap-Spa-Lasso 在8 个数据集上的分类精度

5 结语

文中提出一种特征选择方法模型Lap-Spa-Lasso。该方法利用Laplacian 正则化项保留同类样本的几何分布信息，结合Lasso 方法的稀疏项构造Lap-Spa-Lasso 方法模型。在8 个数据集上进行了有效性实验，并分析在不同参数变化下所提方法的性能表现。除此之外，所提方法在三类分类器（即RBF 核分类器、线性分类器和KNN 分类器）上进行了实验，从分类精度上可以看出所提方法都要优于未引入正则项的Lasso 方法，说明了所提方法有很强的性能表现，从而说明引入正则化项不仅仅能改善分类器性能，而且具有很好的推广性能。然而，所提的特征选择方法最终是需要应用到实际场景中，进一步工作将所提方法应用至医学图像分析、生物标识数据分析中。