死亡率相依模型下的养老保险产品的定价

陈 果，梁 雪

（苏州科技大学 数理学院，江苏 苏州215009）

养老基金行业面临着死亡率风险，也就是未来死亡率的发展趋势和当前假设不相符的风险。传统上，对死亡率的建模是确定性建模。但是，死亡率在近几十年不断攀升，使得人寿保险公司面临着寿命风险，因此，建立更加有效的模型来预测死亡率是十分必要的。到目前为止，随机死亡率模型在学术界和从业者中得到了越来越多的关注。

马尔可夫机制转换模型被广泛地应用于金融保险领域，如梁雪[1]在机制转换模型下考虑可违约权益的对冲问题；Milidonis A 等[2]在马尔可夫机制转换随机模型下对死亡率进行了研究，研究结果显示马尔可夫机制转换模型优于诸如Lee-Carter[3]和Lin-Cox 等[4]一些重要模型。他们还在马尔可夫机制转换模型下考虑与死亡率相关的证券产品的定价，由此发现机制转换随机模型可以修正部分不合理的定价。事实上，许多保险产品是长期合约，因此，将市场制度和环境状况的变化纳入死亡率动态模型中是有实际需求的。受文献[1]的启发，笔者建立了一个马尔可夫机制转换随机模型来对涉及多个生命的保险产品进行定价。文中建立的这一模型考虑了经济环境状况的变化对随机死亡率动态过程的影响，死亡率的动态演化是通过机制转换双散粒噪声过程来描述的，其中纯跳过程可以捕捉到突发性灾害对死亡率的影响。Luciano 和Vigna[5]以及Cox等[6]发现在死亡率模型校准中带跳过程优于扩散过程。

跳扩散模型一直活跃于各种风险模型中，例如，Ma Y[7]等在描述违约聚集性时提出了一种新的跳扩散模型；刘孔洁等[8]在超指数跳扩散模型下考虑了动态保护基金的定价问题；Wang Y[9]等用跳扩散模型来刻画投保人的财富过程。散粒噪声过程是一种纯跳模型，此模型下能够得到金融中许多重要量的显式表达式[10]。在信用风险中，散粒噪声过程可以用来刻画重大事件对违约产生的影响。Artzner 和Delbaen[11]提出保险产品和信用衍生品之间存在着相似之处，用来刻画违约的方法也可以用于描述死亡率。通过对这些过程进行适当地扩展，笔者用带有机制转换散粒噪声的二维跳扩散过程对两个个体的死亡率进行建模。

文章结构如下：第一部分给出死亡率的动态演化过程；第二部分讨论一种取决于已婚夫妇的相依死亡率过程的保险产品的定价问题；第三部分给出数值结果；第四部分是全文总结。

1 带散粒噪声的二维机制转换跳扩散模型

考虑在有限时间T =[0，T*]（T*＜∞）范围内的连续时间模型，令（Ω，F，F，P）为一个完备概率空间，过滤满足通常条件，假设所有的随机变量和随机过程都定义在这个概率空间上，并且是FT*可测的，P 是风险中性概率测度。令X:={Xt|t∈T }是一个连续时间的有限状态的齐次马尔可夫链，其生成的过滤记为具有生成元Q=qij，i，j=1，2，…，N。不失一般性，把X 的状态空间取为单位向量的集合其中符号“′”表示向量或矩阵的转置，马氏链X 刻画了经济环境因素。Elliott R J[12]和Elliott R J[13]等为马尔可夫链提供了半鞅分解

考虑两个当前年龄为yi（i=1，2）的投保人，他们的随机剩余寿命为随机强度λyi的F-停时τyi。此处所考虑的个体是同质队列的代表性代理人，在这一队列中的人的年龄和健康状态相同，且剩余寿命同分布。

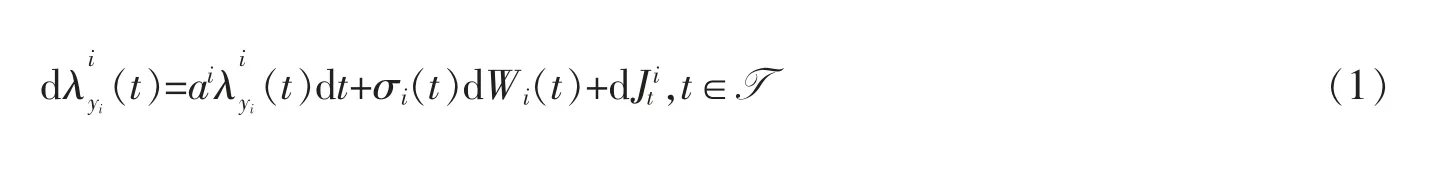
其中ai＞0 是常数，σi（t）由下式给出其中和W2（t）是相关系数为κ 的两个标准布朗运动，它们与其他随机变量独立。对i=1，2，纯跳过程由给出，其中Ni:={Ni（t）|t∈T }（i=1，2，3）是随机强度为ρi:={ρti|t∈T }的Cox 过程。给定HX，假定N1，N2和N3是相互独立的，且对每一个i=1，2，3，跳跃尺度是独立同分布的，其密度函数为和是相互独立的。

bi＞0 是指数衰减率是机制转换的复合Poisson 过程，即其中是机制转换的Poisson 过程，强度为其中对i=1，2，3，j=1，2，…，N，跳 跃 尺 度有 定 义 在（0，∞）上 的 密 度 函 数其 中（gi1（·），…，giN（·））′∈RN。给定HX，假定和是相互独立的和是相互独立的且与其他随机变量是独立的。进一步，假定也是相互独立的。

对i=1，2，3，强度过程ρi生成的过滤记为令是一个二维马尔可夫过程，记

注1在这里，死亡率过程是带散粒噪声的机制转换跳跃扩散过程，它描述了诸如瘟疫、自然灾害或创伤性事件等突发事件对死亡率的影响。当突发事件发生时，死亡率会增加，然后会持续下降到前一个水平，直到另一突发事件发生，这将导致死亡率发生正的跳跃。从直观上来说，假设突发事件的到达强度可以根据经济环境因素进行切换是合理的。另一方面，在突发事件发生后，其再次发生的可能性在未来一段时间内通常会降低。例如，一场大地震发生后，一般在短时间内不太可能再次发生另一场大地震。因此，带散粒噪声的机制转换跳跃扩散过程可以很好地刻画突发事件对死亡率的影响。

注2死亡率过程中跳尺度的密度函数f（y）也可以进一步假设为与表示经济环境因素的马尔可夫链相关，但这会导致解析性的丧失。从直观上看，经济环境因素更有可能影响诸如地震、洪水等突发事件的发生频率，而对由此所引发的死亡率跳跃大小的影响是不大的。因此，文中只是将经济环境因素对突发事件到达强度的影响纳入到定价模型，而忽略它对死亡率跳跃大小的影响。

对任意li≥0，mi≤0，nj≤0，i=1，2，j=1，2，3，记

定理1对任意li≥0，mi≤0，nj≤0，i=1，2，j=1，2，3，有

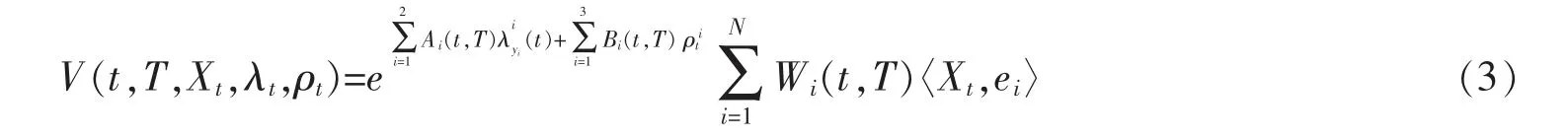
其中，

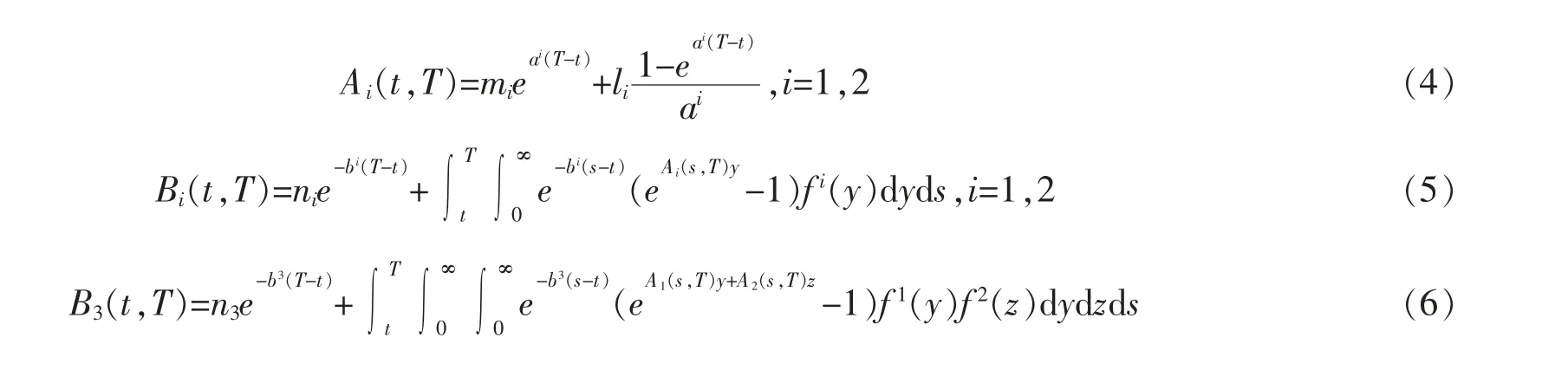
矩阵W1（t，T），W2（t，T），…，WN（t，T）满足下述关系式

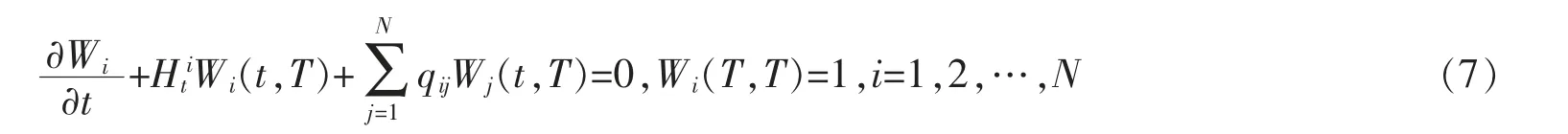
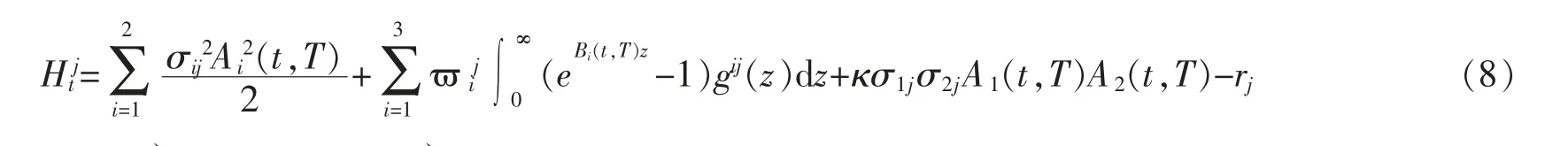
证明记令

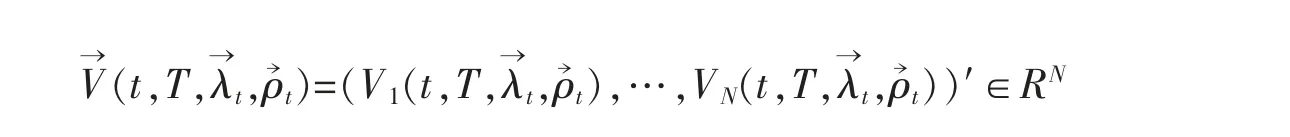
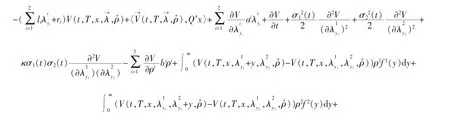
令

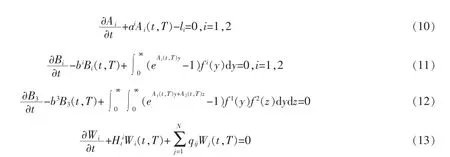
令Ai（T，T）=mi，Bi（T，T）=ni，W（T，T，x）=x，求解方程（10）-（13）即得到结论。

2 养老保险产品的定价

现在考虑一个取决于已婚夫妇的生命存续期的养老保险产品的定价问题，其在T时刻的保费可表示为

其中K＞0 是一个常数，τy1和τy2分别代表了当前年龄为y1和y2的个体（一对已婚夫妇）的剩余寿命。假定τy1和τy2关于H 条件独立，也就是，对任一t1＞0，t2＞0，τy1和τy2的联合生存分布为

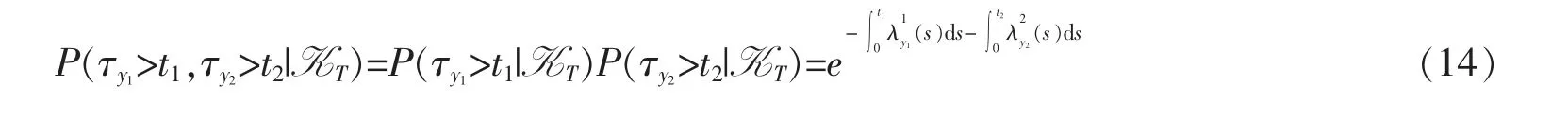
根据定理1，利用条件期望的塔式性质，易得τy1和τy2的联合生存分布。于是这项保险产品的净保费为

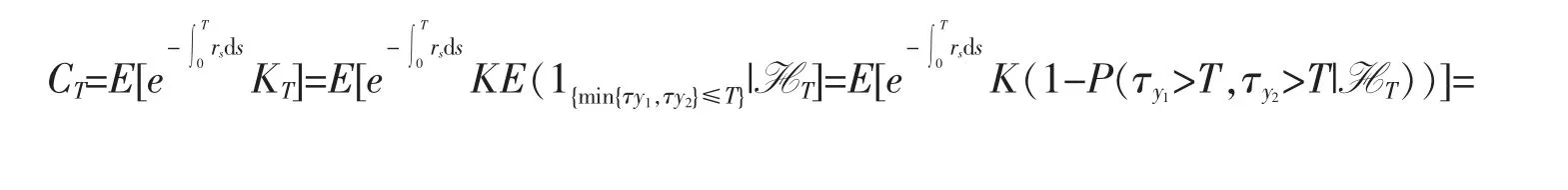
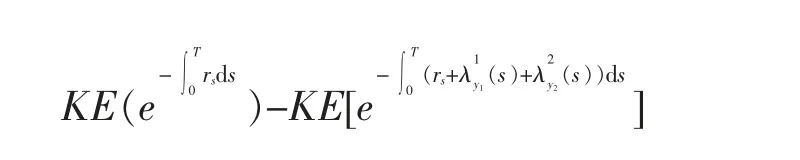
根据Buffington 和Elliott[14]中的Lemma A.1 有

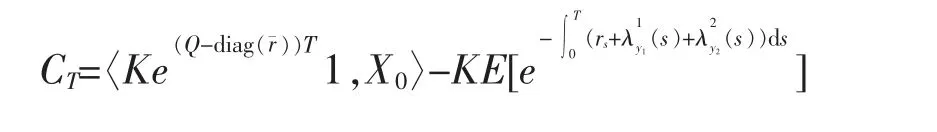
利用定理1，有

其中参数同式（3）-（8），li=1，mi=0，nj=0，i=1，2，j=1，2，3。

注3由式（1）、（2）以及式（14）所建立的死亡率相关结构可以扩展到多变量情况。

3 数值结果

该节对取决于已婚夫妇生命存续期的养老保险产品的净保费进行了一些数值分析，以说明文中的理论结果。

为了便于说明，文中考虑N＝2 的情况，即X只在两种状态之间转换，其中和分别代表“好”的经济环境和“坏”的经济环境。对于净保费CT的计算，除非另有说明，将参数设置如下：K＝1，

图1 显示了净保费C10和q之间的关系，可以看到，当初始经济环境处于好的状态时，即X0＝e→1时，C10是q的一个递增函数，这是因为q越高，转换到状态e→2的概率就越大。从图1 还可以看到α越大，净保费C10越小；图2 显示β 越大，C10越小；从图3 可以看到C10随着a的增加而减少，这些变化趋势都符合实际情况。

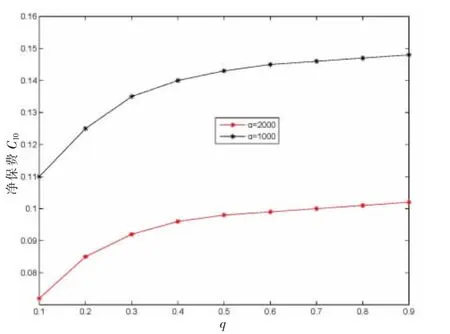
图1 不同α 和q 下的净保费C10

图2 不同β 和b 下的净保费C10

图3 不同X0 和a 下的净保费C10

4 结语

建立了带有散粒噪声的二维机制转换跳扩散模型。在该模型中，利率、死亡率与一个由连续时间有限状态的马尔可夫链刻画的经济环境状况密切相关，已婚夫妇的死亡率相依结构由此模型刻画。最后运用鞅理论推导出取决于已婚夫妇生命存续期的养老保险产品的净保费的指数仿射解。