眼语融合，教会聋生掌握平面几何语言

刘智平 王彩仙 杨忆

【摘要】“图形与几何”是聋校义务教育数学课程标准的一项重要内容。几何知识概念多，专业术语多，知识系统严谨，表达高度简练。聋生由于听力障碍，语言发展水平低，对许多几何语言难以理解或理解不透彻，导致学习困难。

【关键词】义务教育;聋生;平面几何语言

《聋校义务教育数学课程标准（2016年版）》指出：“听觉障碍既严重影响聋生的语言发展，又给数学学习带来困难。如何发挥聋生的视觉认知优势，因势利导地培养聋生的数学素养，是聋校义务教育阶段数学教育必须解决的问题。”“聋校数学教学活动是师生积极参与、交往互动、共同发展的过程。要充分利用聋生视觉优势，采取有效的沟通手段和多元的教学方法，激发聋生学习数学的兴趣。”[1]

眼，即视觉;语，即语言，包含口语、手语和书面语。眼语融合即教学过程中融视觉、运动觉和口语、手语、书面语于一体的课堂教学模式。纵观聋校课堂教学，聋生接受教师传授的知识渠道有且只有一个，那就是靠眼睛看老师“说话”（手语）。特别是平面几何的数学课堂，涉及许多的数字、字母、公式（式子）、图形等，如果聋生没有集中注意力看课（看老师比画手语、看老师口形、看老师板书），那么对于这一堂課所授知识，他们掌握几乎为零。

因此，在几何知识教学中，教师要根据聋生特殊身心特点，眼语融合，教会聋生掌握平面几何语言，从而顺利完成“图形与几何”的教学。

一、眼语融合，文图同现，理解平面几何术语的意义

聋生刚开始接触平面几何知识时，由于学习的内容与之前学习的代数内容存在较大差异，对于一些几何术语，如“任意一点”“每两点”“互相”（垂直、平行）“顺次截取”“有且仅有”等不甚理解，不会运用。

针对这种现象，教师在教学中要充分发挥聋生视觉感知优势的特点，努力教会聋生看懂图，力求做到把平面几何语言与图形、数学符号紧密结合起来，对于每一个新出现的术语，文图结合，一同呈现，引导聋生在观察中思考;教师在仔细讲清其意义的同时，呈现该术语所表达的图形，结合图形实例进行讲解，让聋生通过视觉观察把几何语言文字与图形紧密联系在一起，在几何语言文字与图形之间建立起联系，透彻理解几何语言。

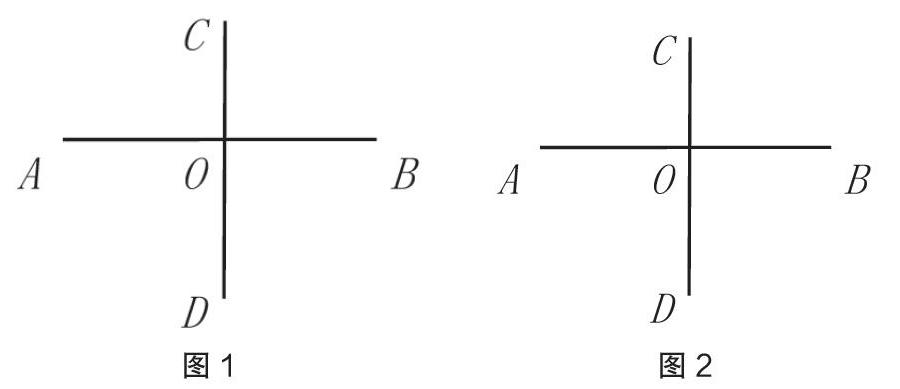
比如“线段AB与CD互相平分”是指AB与CD相交，有一个交点设为O，且AO=BO与CO=DO同时成立，如图1。而图2中虽有AB与CD相交，且AO=BO，但CO≠DO，所以不能称AB与CD互相平分，只可称线段CD平分线段AB。教学中，教师要引导聋生认真观察图1和图2的异同，在黑板上比较、反复指出，让聋生深刻理解互相平分。

二、眼语融合，剖析命题，分清平面几何语言的层次

平面几何命题较多，且命题表达语言简练，逻辑性强。因此，对于命题的教学，既要从语法逻辑的角度进行剖析，又要从聋生学习特点出发，眼语融合，使聋生分清平面几何语言的层次。

如，平行公理中“两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行”的教学，教师先让聋生集体认真“读”题，接着在黑板上画上两条直线，分别命名为AB、CD，问：“两条直线是哪两条直线？”（生答“是直线AB、CD”）“什么是被第三条直线所截？”教师先在黑板上比划多条所截直线的位置（并不需要画出，引导聋生看即可），重点让聋生充分认知、体会什么是第三条直线所截，然后在黑板上画上第三条直线EF。接着，教师再讲什么是同位角及同位角相等，逐层厘清，最后得出“两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行”的结论。

同时适当运用反例教学，提高聋生使用语言的精确性。如让不同聋生相互辨析诸如下列语句：“到一条线段两端距离相等的点是线段中点”“两条线段不平行就相交”“过线段AB外点作AB的垂线”“过MN两点作直线AB的平行线”等。聋生通过自主辨析，分清命题中表达的内容，进而真正掌握知识要点。

三、眼语融合，双向互动，提高逻辑推理能力

聋生的专业语言能力的形成主要来自课堂教学[2]。教学中，教师要强化师生互动、生生互动，要多为聋生提供互动实践机会，让聋生多看（听）、多说、多写平面几何语言的语句，多展示自己的思维过程，提高聋生平面几何语言表达与交流能力，提高逻辑推理能力。

如证明“两直线平行，内错角相等”的教学。已知：a∥b，c与a，b相交.求证：∠1=∠2.（如图3）

证明：∵a∥b（已知）

∴ ∠3=∠2（两直线平行，同位角相等）

∵ ∠3=∠1（对顶角相等）

∴ ∠1=∠2（等量代换）

教学中，教师在黑板上逐步板书论证过程中，必须逐一提问，让同学们说说能得出什么结论，根据或理由是什么。如，师问：“a∥b的理由是什么？”生：“已知。”又问：“a∥b能够得到什么？”生：“∠3=∠2。”师：“为什么？”生：“两直线平行，同位角相等。”……

这样，教师一边问一边板书论证，在师与生问与答的互动过程中，教师要充分利用灵活的眼神表现形式，或扫描全班同学，或紧盯某位同学，或瞪大双眼等，吸引学生的注意，应用略为夸张的手势动作及步伐移动的调节等强调重点，还要运用夸张的口形及丰富的面部表情，有利于聋生及时理解、掌握课堂教师所授知识。

四、眼语融合，手脑并用，促进平面几何语言系统化

识记慢，遗忘快是聋生一大特点。教师要及时督促聋生自觉动手，对已学习的知识要及时复习，对相同或相近的概念进行归类，对易混淆的概念进行对比，让聋生分清所学概念内涵与外延，让这些概念真正为聋生所掌握，使其平面几何语言系统化。

比如，带有“任意”的平面几何语言有：在直线l上任取一点;以已知点为圆心，任意长为半径画弧;过A点任意作一条直线，过三点中的任意两点作直线，等等。又如关于“存在与唯一性”的平面几何语言有：经过两点有且只有一条直线;过一点有且只有一条直线与已知直线垂直;过一点有且只有一条直线与已知直线平行;两条直线相交只有一个交点等等。此外，对于一些平面几何语言的叙述模式和习惯用语，如“连结××并延长交××于××点”“延长××到×，使××等于××”等，要求聋生比较识记，以利于正确地使用。

梳理这些已学习的知识点，要求聋生既要熟记平面几何语言文字表达形式，又要动手作（画）出相关图形，在活动中思考，促使聋生正确运用平面几何语言，使掌握的平面几何语言系统化。

五、眼语融合，规范表述，准确运用平面几何语言

在平面几何课堂教学中，教师规范的板书极大影响着聋生对平面几何语言的理解。教师在黑板上板书呈现的内容要注意与教材表述的语言相一致，做到语言规范化。同时，要引导聋生认真阅读教材，深刻领会规范表述，进而准确运用平面几何语言。

例如，“三边分别相等的两个三角形全等”是聋生学习三角形全等的判定中第一种判定方法，证明中应用规范的书写格式，对聋生后续整个章节的学习影响很大。教学中，不仅要加强师生互动，而且要在板书时着重强调格式书写的规范化，教师在黑板上的板书要与课本例题保持一致，特别是关键书写点，如∵和∴的书写、“在△…和△…中”的书写，应重点向学生强调指出，使聋生在本章节学习的第一节课就掌握规范证明这一题型的规范书写格式，不仅有利于后面整个章节内容的学习，而且有助于逻辑推理能力的培养。

实践证明，数学课堂眼语深度融合，是教会聋生掌握平面几何语言，顺利完成教学任务最有效的手段。

【参考文献】

中华人民共和国教育部.聋校义务教育数学课程标准（2016年版）[M].北京：北京师范大学出版社，2018：291-292.

汪飞雪.听觉障碍学生教学法[M].天津：天津教育出版社，2007：184-185.