大底盘层间隔震结构一体化设计方法研究

杨 奎， 谭 平， 陈华霆， 李晓磊

(广州大学 广东省地震工程与应用技术重点实验室/工程抗震减震与结构安全教育部重点实验室， 广东 广州 510405)

层间隔震体系是在基础隔震体系的发展中演变而来，因其隔震层设置灵活，适用范围广而被广泛应用.祁皑等[1]设置隔震层在不同的位置，验证了层间隔震结构的参数优化理论，并通过振动台试验发现减震效果随着隔震层位置的升高而降低.周福霖等[2]从频谱特性出发，提出了以基底剪力最小原则的层间隔震参数优化准则.李凯达等[3]研究了在大底盘结构不同塔楼量和高度等因素影响下，塔楼之间的相互作用力，并引入差异化系数对多塔结构的相互作用进行评估.张颖等[4]从能量观点出发，推导了基于能量平衡的层间隔震结构最大变形、隔震层最大剪力等地震响应预测公式.

随着隔震技术的推广，我国《建筑抗震设计规范》[5]提出了分部设计法，但仅以设防烈度地震作用下时程分析的减震系数作为降度设计的标准，设计结果取决于选取的地震动，减震效果的精准性无法保证.针对层间隔震这类非比例阻尼特性显著的结构，目前我国对其直接分析常用的方法是强制解耦法[6-8].Warburton等[9]认为强制解耦法对非比例阻尼特性较强的结构会产生较大的误差.陈华霆等[10]基于Benchmark隔震模型对复振型分解反应谱方法、强迫解耦假定下的反应谱及时程分析方法进行了对比，并得出当隔震层阻尼超过10%时，强迫解耦方法的精度较低的结论.由于强迫解耦法缺乏理论依据，所以很多科研人员致力于复模态分解反应谱法的研究[11-12]，然而复模态分析非比例阻尼结构需要同时应用各振型的位移与位移响应和位移与速度响应，增加了分析难度，并且需要解决基于复模态分析的峰值响应组合问题，不利于工程实践应用.周锡元等[13]推导出了完全实数形式且简明的复振型完全平方组合(CCQC)方法，很好地解决了上述问题.针对上述存在的问题，提出能综合考虑结构非比例阻尼特性和支座非线性的隔震设计方法成为迫切需要解决的问题.

本文以层间隔震结构为研究对象，首先对其进行等效线性化，然后基于复振型分解原理与CCQC组合准则介绍了一体化设计方法，并将此设计方法与传统的分部设计方法楼层剪力分布和经济性方面进行分析.此外，以30条人工波的非线性时程分析平均值为精确解，讨论非比例阻尼对层间隔震结构的计算误差，最后对采用两种设计方法的相关构件内力等指标进行了分析讨论.

1 层间隔震结构非线性运动方程

对于大底盘层间隔震结构，隔震层以下结构楼层屈服强度往往较大，考虑到隔震装置的竖向刚度远大于水平刚度，在进行地震响应分析时，可以近似地认为结构只作平动而忽略其竖向变形引起的摆动，分析模型如图1所示.图1中mi,ki,ci,xi分别表示各楼层质量、刚度、阻尼系数和相对地面楼层位移，b表示隔震层.

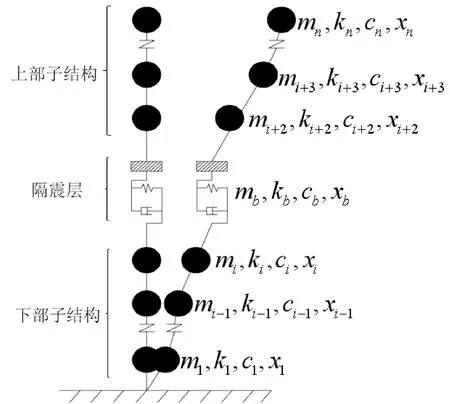
图1 层间隔震结构分析模型

在强烈地震作用下，由于隔震层以下结构楼层屈服强度一般较大，假设只有隔震层会进入非线性.隔震层中支座滞回模型取为双线型，其恢复力表示可分解为弹性力和滞变力之和[14]，如下式表示：

f(Δ,z)=αk0Δ+(1-α)k0z

(1)

Δ是隔震支座水平变形，k0是初始刚度，α是屈服后刚度ky与k0之比，z是滞回位移.

(2)

y=(y1,y2,…,yn)T，yi=xi-xi-1表示结构的层间位移向量，r=[1,…,1]T为地震影响向量，z表示滞回位移向量，其中质量矩阵M、阻尼矩阵C、线弹性刚度Ks以及塑性刚度Kz：

2 隔震支座等效参数迭代

为了在层间隔震结构设计中采用一体化设计，必须对隔震支座进行等效线性化.国内外对双线性模型进行等效线性化方法有很多,比如Dicleli等[15]和Hwang等[16]提出的非割线刚度法，我国学者曲哲等[17]也提出了相应的割线刚度法.考虑到实施的方便性和和精准性，本文采用Rosenblueth等[18]提出的割线刚度法，它采用最大位移对应的割线刚度作为等效刚度，并以实际模型与等效模型在一个周期内的耗能相等为原则，确定其等效阻尼系数，该方法不仅简单，而且在隔震结构中应用较多.其迭代原理如图2所示.

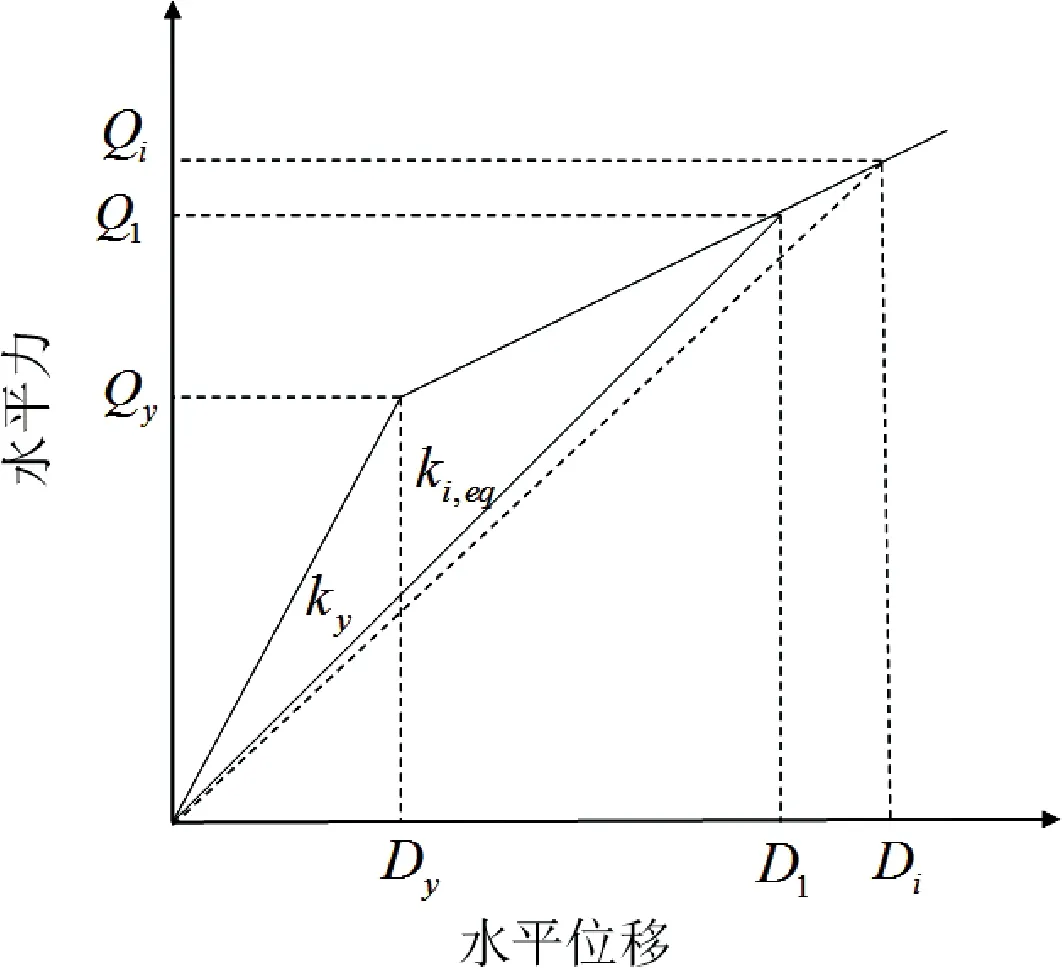
图2 等效迭代原理图

首先假定隔震支座初始水平位移D0(设防、罕遇地震作用下分别取100%、250%剪应变对应的位移值)，通过计算上部子结构荷载可以得到每个铅芯橡胶支座所分担的质量mi，则不同的铅芯橡胶支座的等效刚度keq,i、等效阻尼ξeq,i和等效阻尼系数ceq,i可由下式计算：

(3)

(4)

(5)

式中，ki,j为第j个铅芯支座的第i次迭代后的屈服后刚度，Qy,j为第j个铅芯支座的屈服力，Di为第i次铅芯支座的初始位移，Dy,j为第j个铅芯支座屈服位移.

由式(4)可以看出等效参数依赖于隔震支座的位移响应，需要迭代求解，其流程图如图3所示，具体步骤如下：

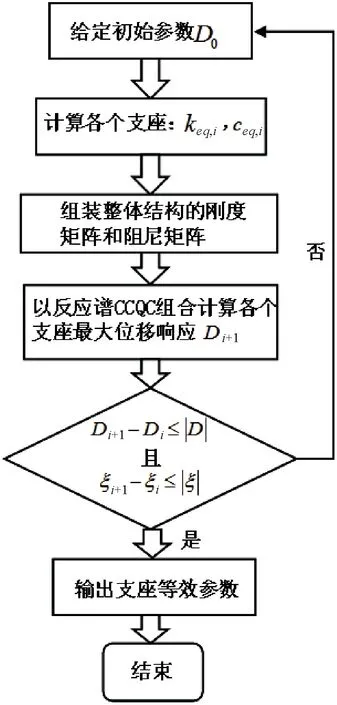
图3 等效迭代流程图

(1)以隔震支座的初始刚度作为刚度初值形成结构整体刚度矩阵，隔震支座对应的阻尼矩阵为0；

(2)利用下一节介绍的复振型分解反应谱CCQC组合计算出各个隔震支座的位移响应，代入式(3)～式(5)求得等效刚度和等效阻尼系数；

(3)将等效刚度系数和等效阻尼系数组装成新的刚度矩阵和阻尼矩阵；

(4)重复步骤(2)、(3)直至满足收敛条件，收敛条件见参考文献[19].

3 层间隔震复振型分解反应谱方法

通过等效线性化后运动方程可表示如下：

(6)

式中,Ceq为非经典阻尼矩阵，Keq分别为铅芯橡胶支座等效线性化后的刚度矩阵.

为对上述方程进行解耦，利用Foss变换[20]需要将其转化为2n个一阶微分方程，即

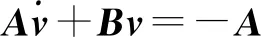
(7)

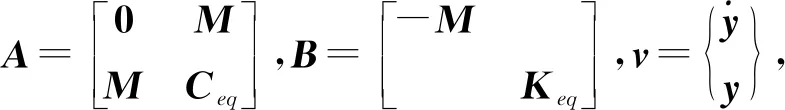
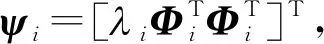
(8)

式中，Re(·)和lm(·)分别表示取复数的实部和虚部.

利用复振型叠加方法，位移向量y可展开为

(9)

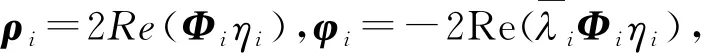
(10)

在工程实践中，通常关心的反应量有层位移、层间位移以及剪力、弯矩等，这些反应量是与位移相关的，故任意地震反应量R(t)=νTy(t)，ν是响应转换向量，与结构的几何、物理属性有关.利用式(9)，R(t)可进一步表示为

(11)

式中，αi=νTρi，βi=νTφi.

(12)

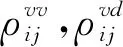
振型相关系数表达式如下(r=ωi/ωj)：

(13)

(14)

(15)

上述的振型组合是非比例阻尼线性系统的反应谱叠加公式，也称之为CCQC反应谱方法，与传统的经典阻尼体系的CQC组合不同，它包含了振型速度响应的成分.

4 层间隔震结构一体化设计方法

目前国内隔震设计大多采用《建筑抗震设计规范》GB50010-2010中提出的分部设计法，如图4所示，其核心是，首先通过对整体结构进行时程分析求得减震系数β，然后利用减震系数β对上部子结构进行降度设计.这种方法将上部子结构和隔震层分开，通过减震系数来考虑隔震层对上部子结构的影响.然而，上部子结构的地震作用分布与整体分析时的是不同的，特别是靠近隔震层位置的楼层.同时，减震系数β是基于时程分析确定，由于地震动的随机性，这会导致减震系数会有一定的离散性，不容易把握.此外，对于层间隔震结构，上部子结构按降低设防烈度进行设计，而下部结构按隔震后设防地震的抗震承载力要求设计.隔震层对下部子结构的响应又需要在罕遇地震下考虑，这个过程十分繁琐.

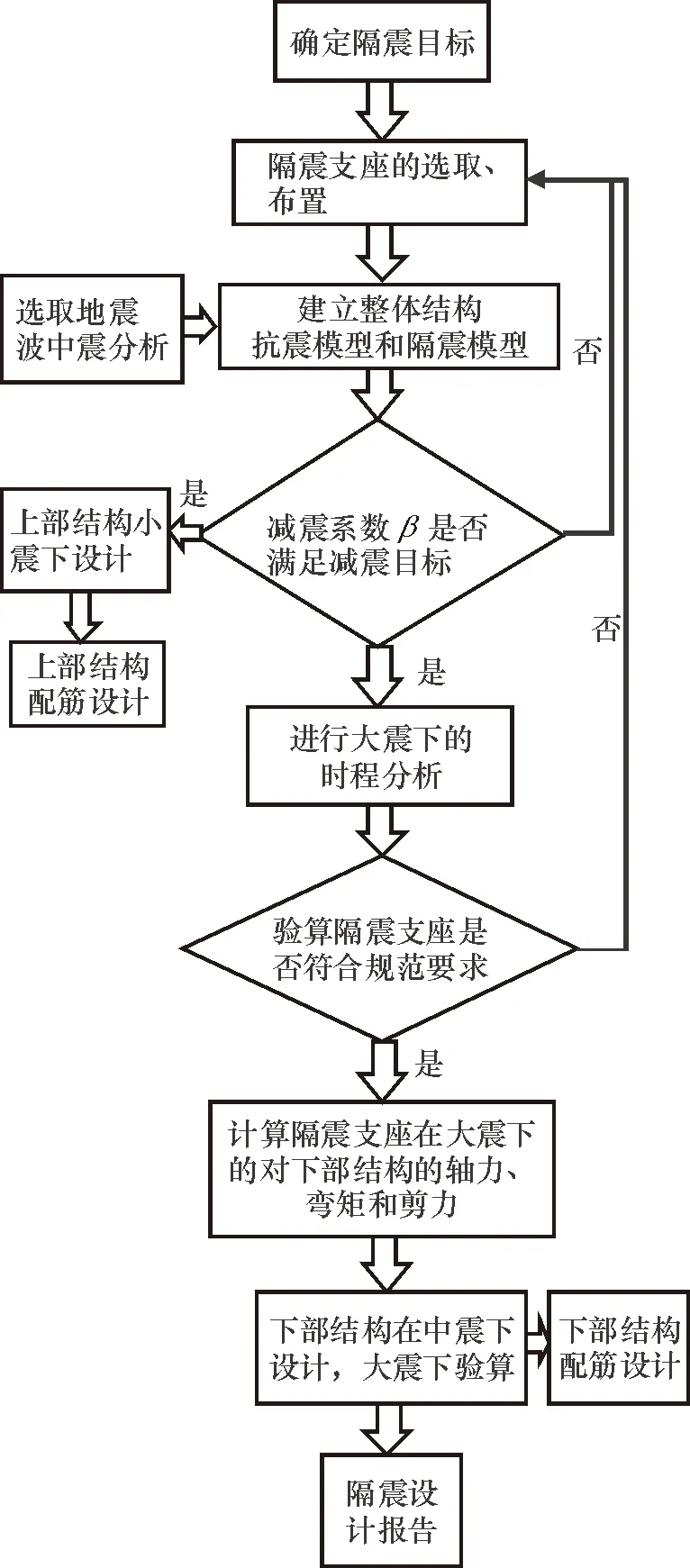
图4 层间隔震分部设计流程图

目前，传统的反应谱方法CQC方法应用于隔震结构时需要借助强迫解耦的手段，即不考虑非比例阻尼的影响，主要适用于隔震层阻尼不大的情况；另一种方法是本文介绍的反应谱CCQC方法，可以充分考虑非比例阻尼的不利影响,其设计流程如图5所示.

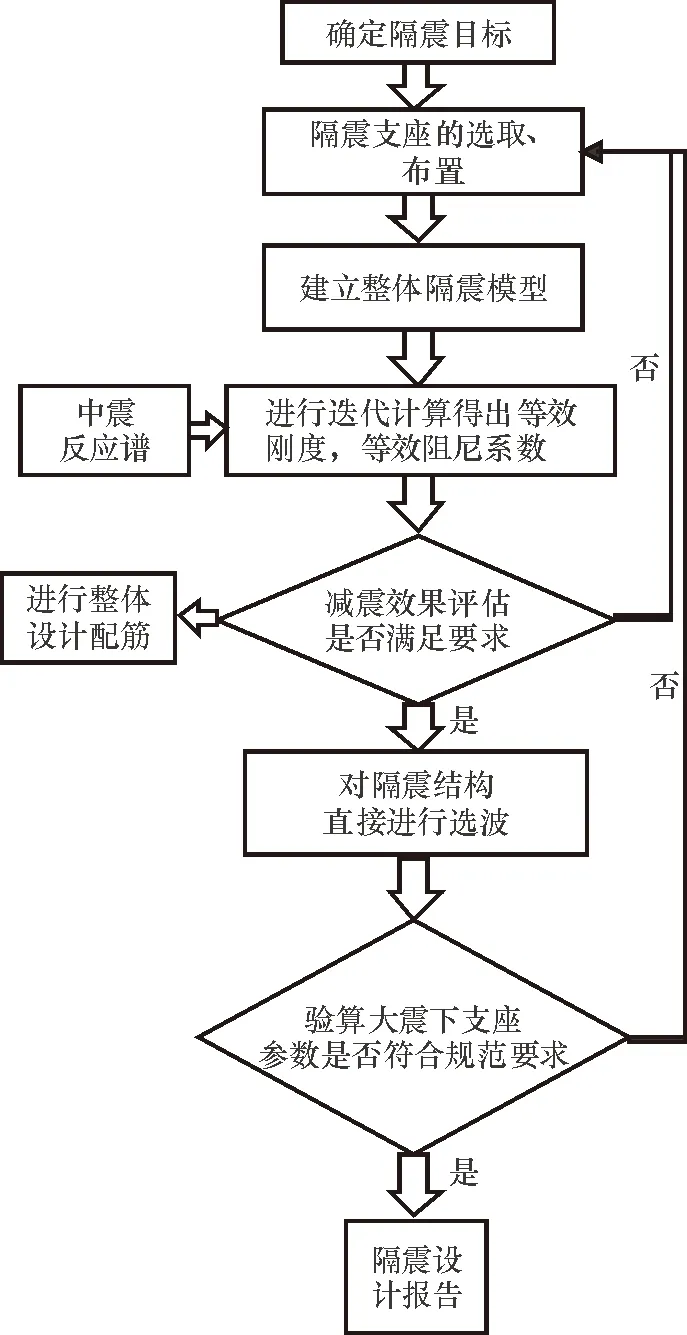
图5 层间隔震一体化设计流程图

反应谱CCQC方程的具体步骤如下：

(1)首先确定隔震目标；

(2)建立有限元模型，根据竖向荷载选取支座，并确定支座布置方案；

(3)建立隔震有限元模型，利用第2节的迭代方法对隔震结构进行等效线性化，求取支座等效参数；

(4)进行一体化设计分析，通层间位移角，判断结构有没有达到中震弹性要求，并进行配筋计算；

(5)对隔震结构直接选波，验算支座在大震下是否符合规范要求；

(6)整理隔震设计报告.

5 算例分析

5.1 工程概况

以大底盘的框架结构为研究对象，结构1～3层为大底盘，每层4 m；第4层为隔震层，高2 m；5～15层为单座塔楼，每层3 m，总高度47 m.标准设防类建筑，抗震设防烈度均为 8度，设计基本地震加速度为 0.2 g，Ⅱ类场地，设计地震分组为第二组，场地特征周期为 0.4 s.其中，框架结构抗震等级为Ⅰ级.采用隔震设计后，本文选用铅芯橡胶支座(LRB)和天然橡胶支座(LNR).框架的三维模型及隔震支座平面部置图如图6所示.

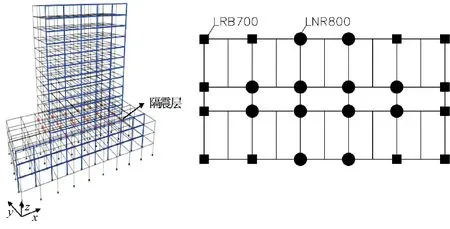
图6 隔震结构有限元模型及支座平面部置图

本文假定所有的天然橡胶支座(LNR)恢复力曲线均为理想线性，不提供附加阻尼比.从表1和表2可以看到一体化设计法与分部设计法对支座的性能参数取值差异较大. 以非线性时程分析的结果为准(隔震层位移118.2 mm)，从表2可以看出隔震层等效线性化后位移为118.6 mm，与非线性时程分析结果相近(表中LRB700n表示迭代后的支座).在随后的计算结构分析中，结构阻尼比皆为表2中的等效阻尼比18.8%.

表1 支座参数

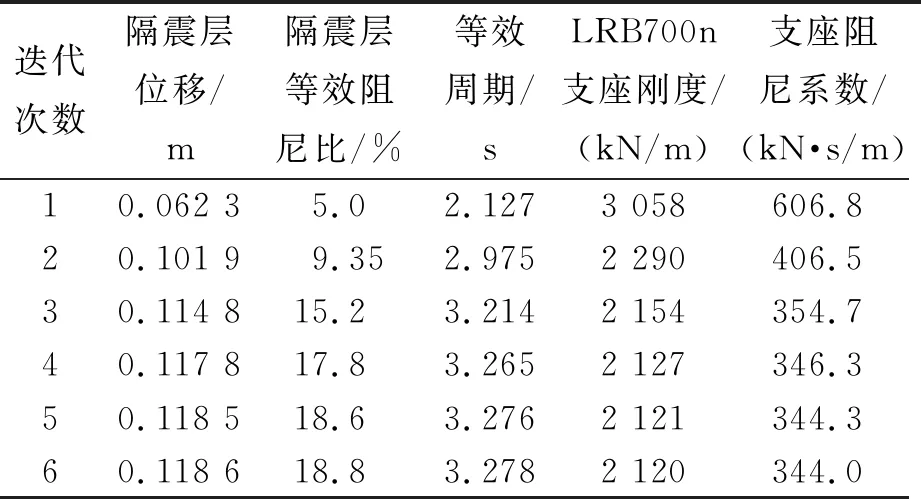
表2 隔震支座等效迭代结果

5.2 层间隔震结构一体化设计与分部设计

为了对比分部设计法和一体化设计法的不同，两种方法均采用同样的支座布置方案.一体化设计反应谱和分部设计法地震波选取如图7所示.

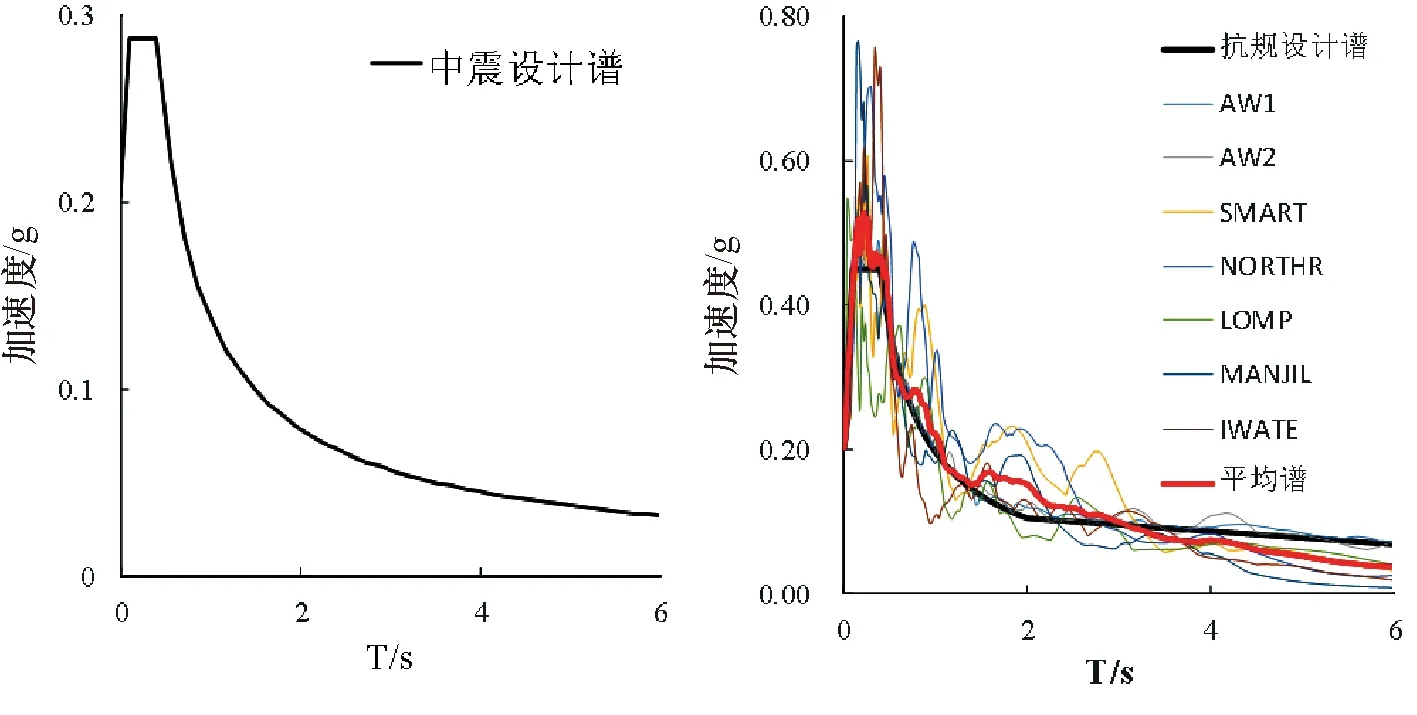
图7 一体化设计反应谱及分部设计地震动

分部设计法是考虑减震系数后对上部非隔震结构进行小震设计，求得减震系数在0.24～0.40之间，按照抗规要求对上部子结构采用降一度小震设计，并将隔震后上部子结构在罕遇地震下支座对下部子结构的轴力、剪力以及弯矩以静力方式加载在下部子结构，抗规规定其按设防地震作用进行设计.本文一体化设计方法是基于中震反应谱对结构进行整体设计.图8给出了两种设计方法楼层剪力和层间位移角.

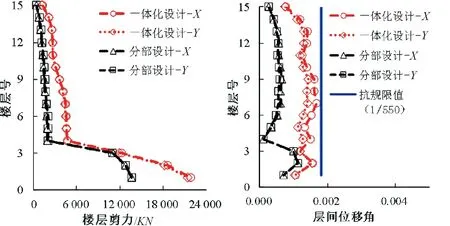
图8 两种设计方法楼层响应对比

由图8可知，在上部子结构，两种设计方法楼层剪力分布是不同的，在靠近隔震层附近楼层剪力差别最大.因为本文提出的一体化设计方法楼层剪力分布考虑了隔震层引起的边界效应，以及上部子结构的惯性力；分部设计则无法考虑这些方面，这会导致结构的配筋分配不合理.再从上部子结构层间位移角可知，分部设计方法最大层间位移角在第9层的X方向1/1 428，满足抗规的弹性设计要求，并且远远小于限值，这样可能会误导设计人员，造成结构不安全.一体化设计方法最大层间位移在第7层X方向1/588，小于抗规给的弹性位移角限值(1/550)，且两者十分接近，可以使设计人员充分考虑设计安全冗余度，提高结构的安全性.

由于一体化设计方法是基于中震弹性设计，从层间位移角可知虽然可以提高结构安全性，但是随之经济性可能会低于分部设计方法，图9给出了分部降一度和一体化设计方法的楼层单位面积配筋图(楼层配筋总量与楼层面积比值)和配筋总量.

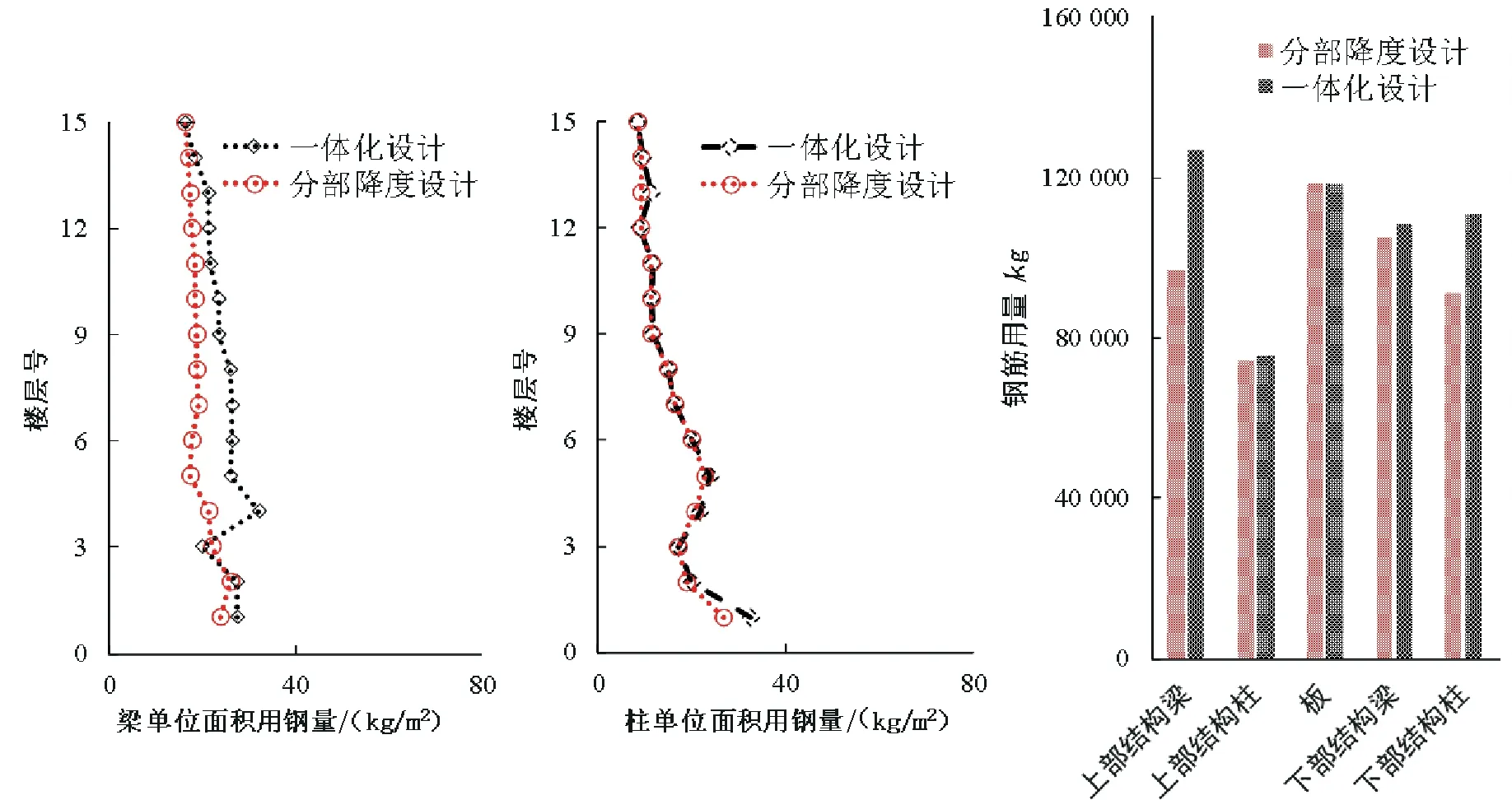
图9 两种设计方法的用筋量对比

从图9中可以清楚的看到一体化设计方法与分部设计的配筋分布明显不同，在隔震层附近梁的配筋是明显大于分部设计方法，分部设计将上部荷载以静力方式加载在下部子结构，没有考虑上部子结构惯性力等因素，显然整体分析配筋分布是比较合理的.从配筋总量看，上部子结构梁用筋量相对多30%，柱的用筋量相当,是由于按构造配筋就可以保证结构安全；下部子结构一体化设计方法梁的用筋量相对多3%，柱的用筋量多于2%.由此可见，两种设计方法仅在梁的配筋上相差较大，因此，可以对结构定义关键梁构件，进行性能性设计，进一步提高结构安全性和经济性.对下部子结构，一体化设计法的柱子用筋量是大于分部设计法的，由于层间隔震结构的下部子结构安全性决定着整个结构的安全，因此，这种现象是符合设计思想的.

5.3 非比例阻尼对隔震设计的影响

为讨论非比例阻尼特性对层间隔震结构反应谱设计影响.采用一体化设计CCQC方法、一体化设计CQC以及非线性时程分析，对此结构进行地震响应分析，并以非线性化时程分析结果为精确解.由于天然地震动离散性较大，所以本文的地震输入全部采用人工波，图10分别为30条人工波的反应谱及其平均反应谱与设计谱的对比.

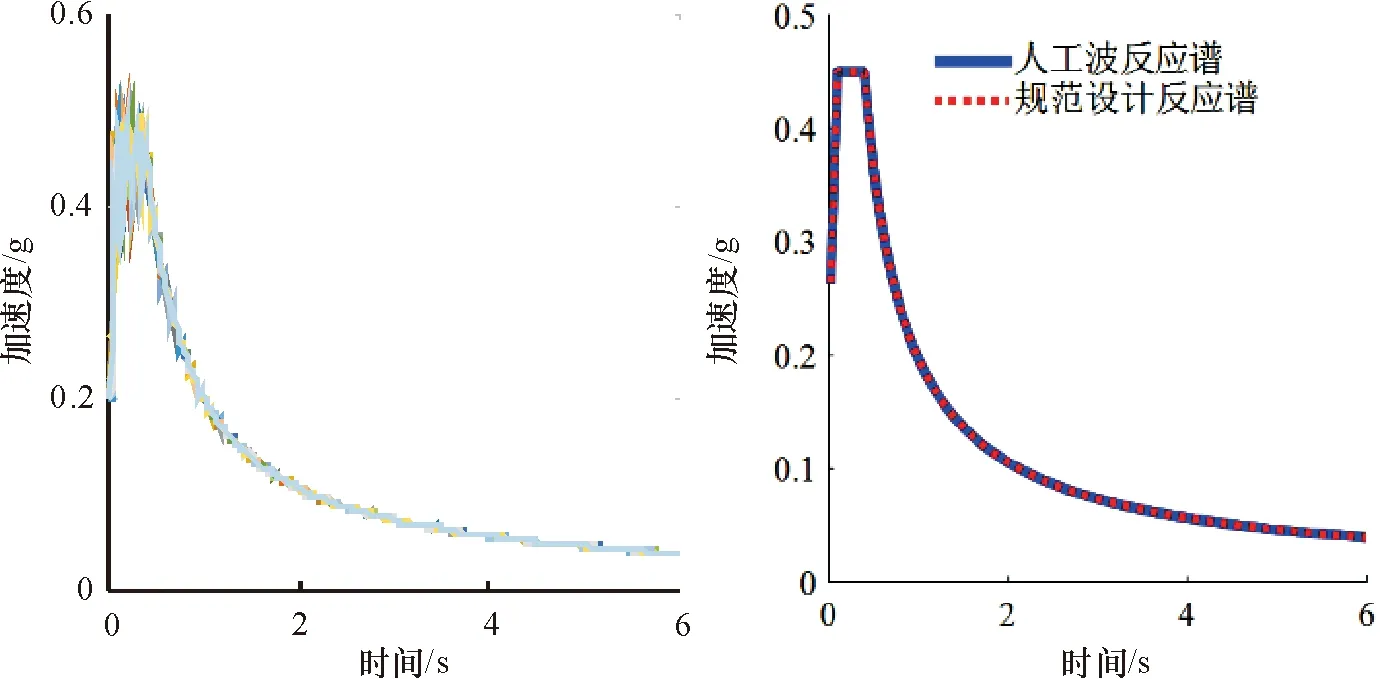
图10 30条人工波平均反应谱与设计谱

图11给出了一体化设计方法相对非线性时程分析的楼层剪力相对误差分布情况.考虑了非比例阻尼特性的一体化设计方法CCQC(以下简称CCQC)，而没有考虑非比例阻尼特性的设计方法CQC(以下简称CQC).

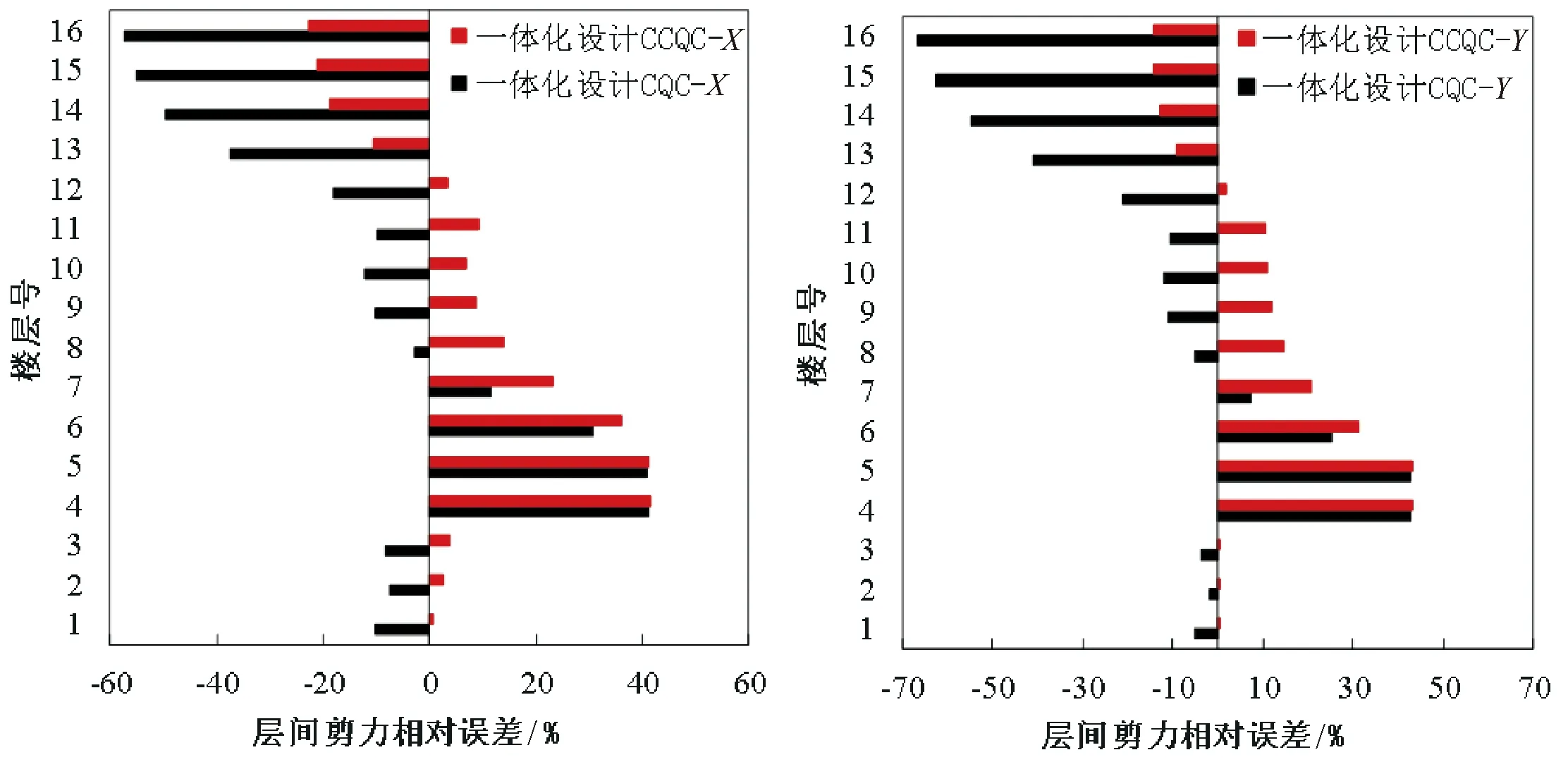
图11 X及Y方向地震作用下楼层剪力响应和相对误差

从图11可以看到，两种反应谱方法的楼层剪力结果相差较大.CCQC方法在整体分布上相对误差(相对误差=(CCQC或者CQC-EXACT)/EXACT×100%，EXACT为时程分析结果)都是偏小的，即小于时程分析结果，其中在隔震层上部子结构，随着楼层高度的增加，剪力相对误差值具有先大后小再变大的趋势，其X方向最大误差在顶层偏小57%，Y方向最大误差依旧在顶层偏小69%.在隔震层下部子结构，楼层剪力偏小10%左右，Y方向偏小5%左右；反观CCQC方法在整体分布上，除顶部楼层外，其它楼层剪力都相对偏大，其X方向最大误差在第四层，偏大44%，Y方向最大误差仍然在第四层，偏大43%；对下部子结构，CCQC法得到的楼层剪力则相对偏大，X方向在2%左右，Y方向在0.1%左右.从中可以看出两种设计方法对剪力分布重点不一样，层间隔震结构对下部安全格外需要重视，CCQC方法重点刚好在隔震层附近和下部子结构，相对正确值都偏大，而CQC方法则不能体现这一点.由此可以看出，非比例阻尼对层间隔震结构的设计影响是无法忽略的.

取出图6中蓝色标记一榀框架(图12)，对该框架梁柱的剪力和弯矩进行分析，图13和图14给出了该榀框架在两种方法下，梁柱构件包络值与相应的非线性时程分析结果的相对误差分布.由于结构比较规则，所以只取X方向地震力进行对比分析.

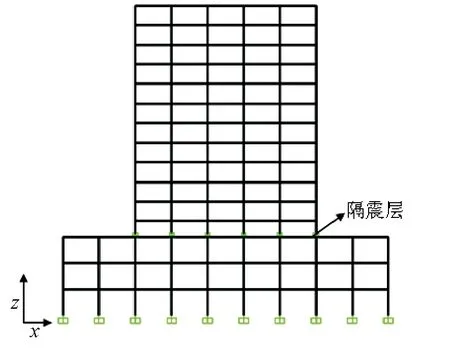
图12 一榀框架示意图

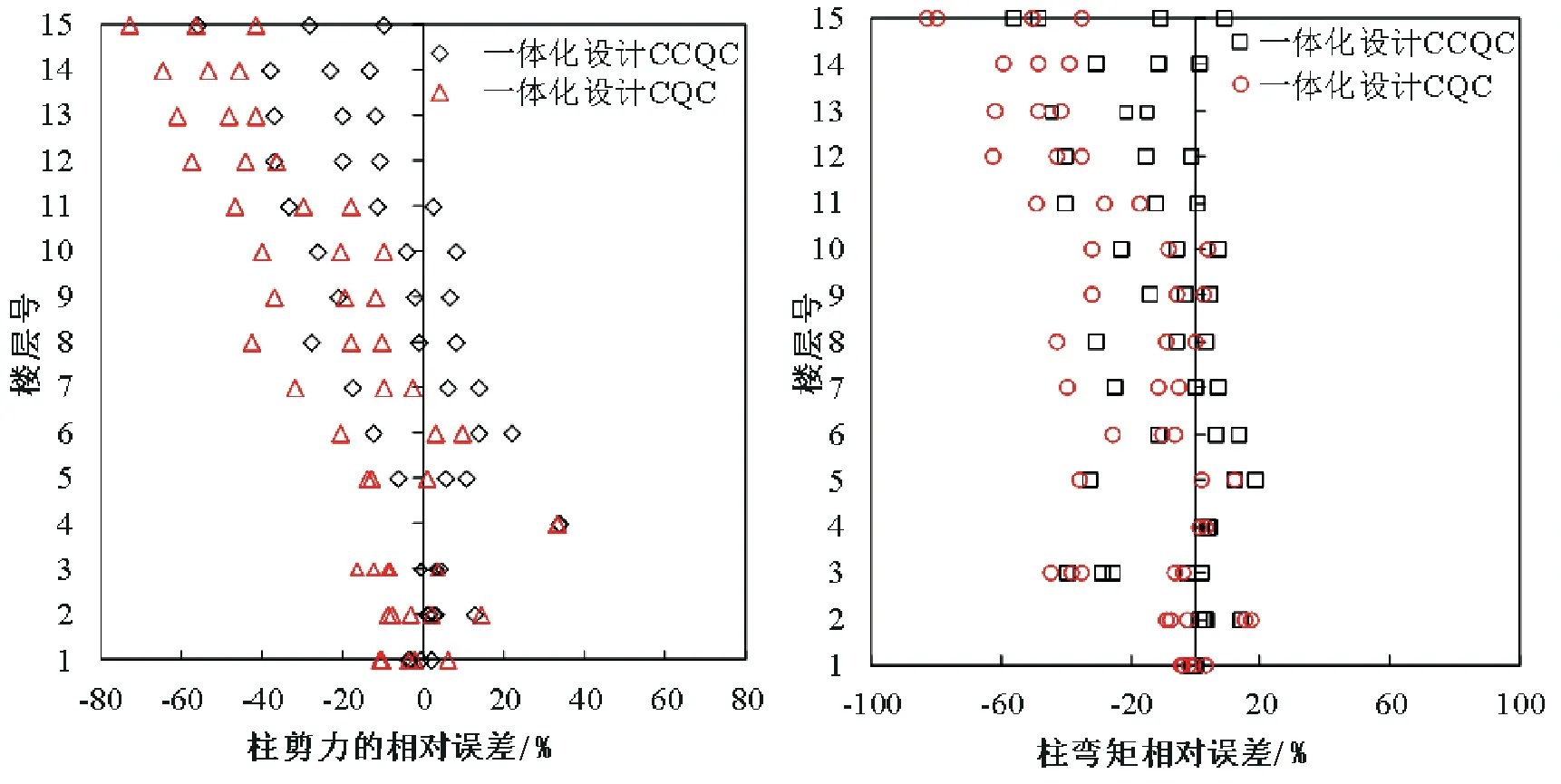
图13 一榀框架各层柱的包络内力相对误差

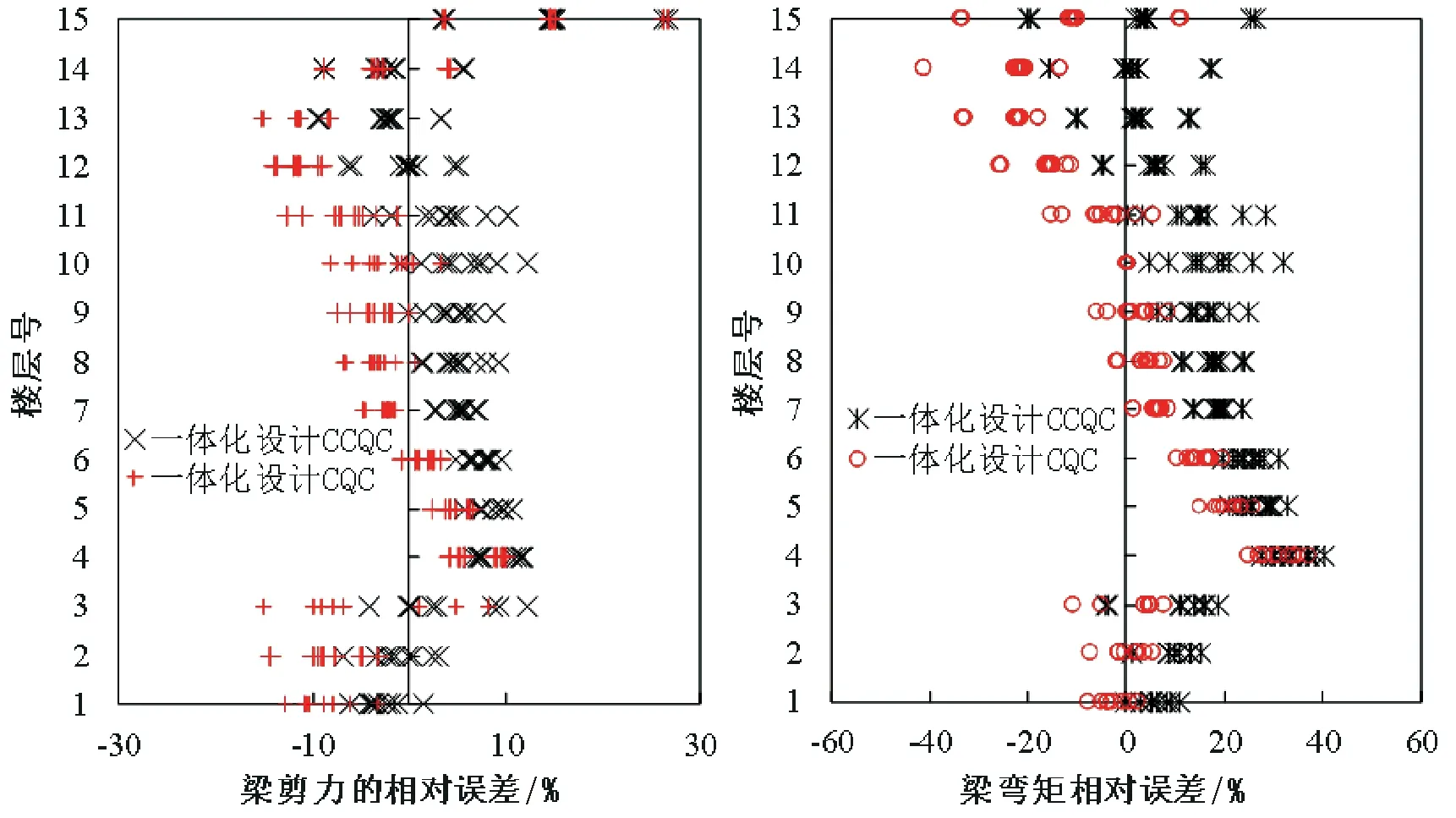
图14 一榀框架各层梁的包络内力相对误差

从图13柱的相对剪力误差分布可以看出，不同位置的构件剪力误差不同，随着楼层的增加误差越大且趋向于偏小，隔震层以下结构两者方法的计算结果精度是相当的，误差在5%以内；隔震层上部子结构，两种方法的误差都随着楼层的增加而加大，且相对于精确值都偏小，除边柱之外， CQC的结果误差在5%～70%之间，最大误差在顶层的边柱，达到了79%.而CCQC方法误差结果在0.5%～40%，最大误差在顶层边柱，达到了50%.从柱的弯矩相对误差图可以得出CQC方法计算结构整体上的趋势还是偏小的，最大误差在顶层边柱，达到了80%.但是CCQC除在边柱处弯矩偏小50%左右，其它楼层偏小在20%之内，并且在中间层CCQC较精确解偏大在20%左右.上述表明层间隔震结构的非经典阻尼特性对结构构件内力的影响较大，进而对结构配筋会产生比较大的影响，对于采用层间隔震技术的工程，在进行实际设计时应考虑非比例阻尼的影响.

图14中，构件梁的剪力相对误差在结构顶层两种方法的误差相同，且相对于精确值都偏大30%左右.其它楼层，CQC方法相较于精确值偏小20%左右，CCQC方法则偏于保守，偏大15%左右，结果比较符合我国的设计思想.从梁的弯矩误差图中，可以明显看到CCQC方法的结果都偏大，最大误差在隔震层的上一层，偏大40%左右；CQC方法在梁的相对误差中，在10层以上时，相对于精确解偏小5%～40%，这对于实际应用来说是不能接受的.从梁的弯矩相对误差角度来看，CCQC方法虽然误差相较与精确解偏大，使得设计偏于保守，对结构安全是比较友好的.

为了进一步探究非比例阻尼特性对层间隔震结构的经济性影响，分别统计两种设计方法的结构楼层单位面积配筋量(图15).

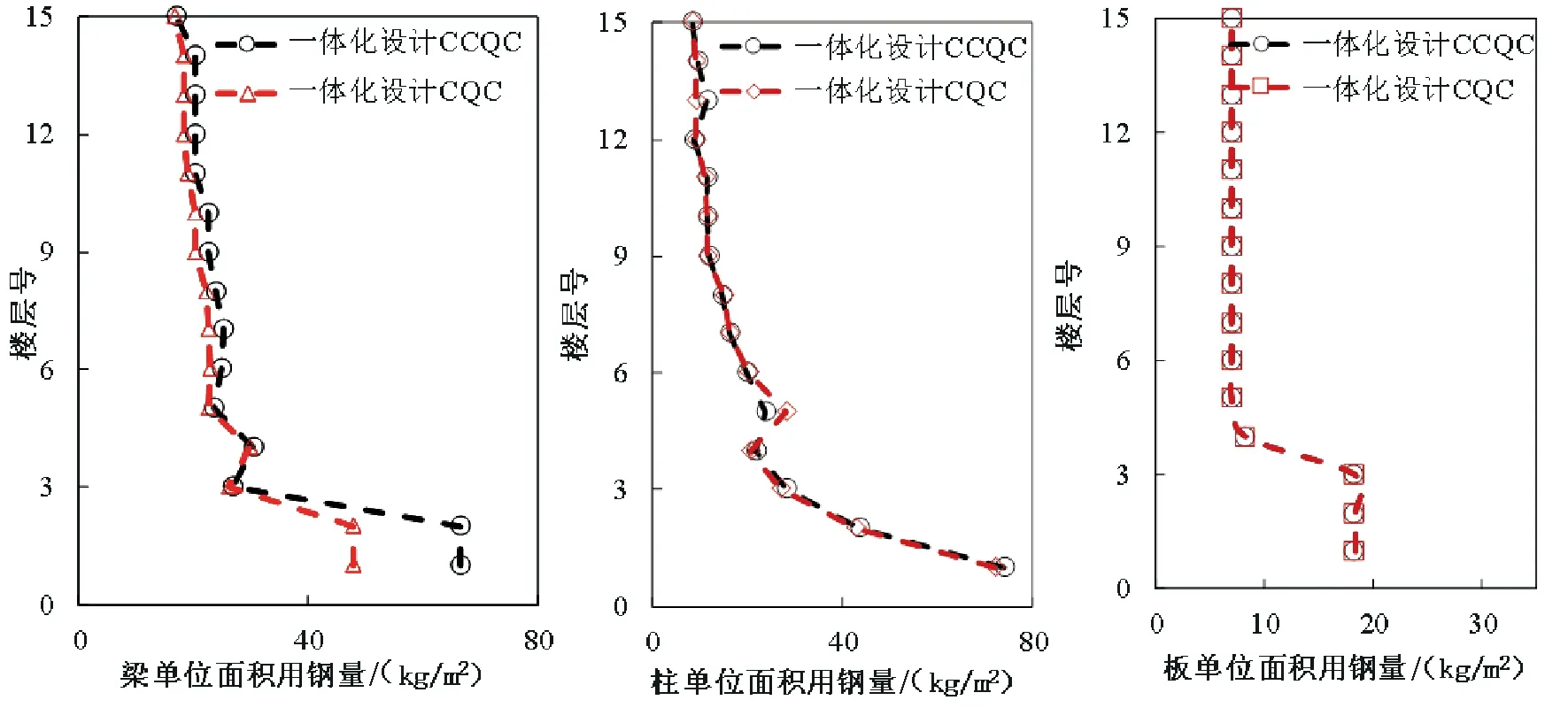
图15 结构梁柱板单位面积用钢量

从图15中可知两种设计方法中，板的单位面积用钢量是相同的，但是可以看到二者梁的单位面积用钢量具有明显的差别，结合上述梁构件内力分析可知CCQC方法计算结构偏保守，显然它的梁的单位面积用钢量是偏大的；一到二层CCQC比CQC多出38%，隔震层上下层多出2%左右，其余层则多出7%～12%.在柱的单位面积用钢量图中，两种方法在隔震层以上的差别非常小，可以忽略不计，但从上述柱内力误差分布来看，两种方法在具体柱构件的配筋分部是不同的，在裙房中误差都偏小且数值较大.CCQC的计算结构都偏大，比较符合设计特点.

6 结 论

(1)本文提出了层间隔震一体化方法，能同时考虑层间隔震结构的非比例阻尼特性和隔震支座的非线性.设计方法可以简化设计步骤，提高结构抗震性能，相对现行分部设计法可以更真实地反映隔震支座在地震作用下真实的状态.

(2)层间隔震一体化设计方法可以考虑隔震层边界效应，以及上部子结构对下部真实的作用力，使得在楼层剪力和楼层配筋上分布更趋合理.

(3)考虑非比例阻尼影响的一体化设计CCQC方法相对于不考虑此影响的一体化设计CQC方法，楼层剪力的误差会偏小.尤其是对下部子结构，CCQC方法能准确的评估其内力，并且是偏大0.1%～2%，而CQC方法则是偏小5%～10%；对于具体梁柱构件，梁柱的弯矩和剪力，一体化设计方法的结果都是大于CQC的，两者相对于精确解的误差都会随着楼层的增加而增加，这种现象在设计时应该予以解决.

(4)对于大底盘框架层间隔震结构，考虑非比例阻尼影响，单位面积框架梁的配筋量是有明显增加的，尤其隔层下部子结构，增加量达到30.88%，在进行此类结构设计时应注意进行关键梁构件定义，进行性能化设计，让配筋分配更加合理，保证安全性和经济性.