一类基于车险数据的改进Copula回归模型

罗丹娜， 王达布希拉图

(广州大学 经济与统计学院， 广东 广州 510006)

在非寿险中，对保单总损失进行估计是一项重要的精算任务.一方面，非寿险产品的保费由保单的期望损失来制定，对损失估计的准确与否将给保险费率的厘定带来直接影响.另一方面，保险准备金的计提也与保单的期望损失有关.因此，保单损失的估计对保险公司的风险管理也具有至关重要的意义.

在传统的总损失预测模型中，通常对索赔频率和索赔强度分别进行预测,即常见的频率-强度模型，将索赔频率和索赔强度的预测值相乘即得总损失的预测值.对索赔频率和索赔强度分别建立预测模型可以揭示索赔频率和索赔强度的不同影响因素，从而有利于风险的识别和管理.然而，该方法隐含着一个重要的假设，即索赔频率和索赔强度是相互独立的[1]，而这种独立性假设并不可能总是成立.例如，Gschlößl等[2]使用完整的贝叶斯方法分析了综合的汽车保险数据集，并检测到索赔强度与索赔次数有一定的相依关系.此外，独立性的假设过于严格，会导致对保单损失的系统性高估或低估，这显然影响了保险组合损失估计的准确性.

尽管如此，现有的关于放松独立性假设的研究仍然很少.截至目前，关于索赔频率和索赔强度相依关系的模型可以分为四类：Copula相依模型[3]、条件相依模型[2,4-5]、共同随机效应模型[6-7]以及相依性调整模型[8].

关于索赔变量间的相依性度量研究中，Czado等[9]及Krämer等[3]利用Copula回归模型使索赔相依性深入到复杂协变量中，但其对变量的边际分布往往主观直取，缺乏一定的客观性.为进一步完善其建模方法，本文基于一组实际数据，用变量筛选和模型选择的相关方法对边际分布做出客观选择.本文选择二元Frank Copula函数联合索赔次数和索赔强度的边际分布，给出保单总损失的拟合分布，并进行相应的实证分析.

1 Copula回归模型

1.1 二元Copula模型

Copula是具有均匀边际的多元分布函数，为构造多元分布提供了自然的方法.其中，一个二元Copula C:[0,1]×[0,1]→[0,1]是[0,1]×[0,1]上具有均匀边际分布函数的二元累积分布函数[3]. Sklar[10]证明了Copula的存在性.

Sklar定理(在二元情况下) 对于具有一元边际分布函数FX和FY的二元随机变量(X,Y)的每个联合分布函数FX,Y，都存在一个二元Copula C，使得

FX,Y(x,y)=C(FX(x),FY(y))

(1)

如果X和Y是连续随机变量，则Copula C是唯一的.反之，如果C是Copula，则上式定义具有边际分布函数FX和FY的二元联合分布.

依Sklar定理，Copula模型的建立主要分为两步：①确定边际分布；②选取一个适当的Copula函数C，以便建立随机变量间的联合分布.

1.2 边际分布的确定

本文考虑索赔强度X和索赔次数Y的联合分布，由索赔变量本身的特点可知(X,Y)是一对取值均为正值的连续-离散型随机变量.

对索赔强度X，本文初步假定服从某分布，如对数正态分布LOGNO(μ,σ2)，其密度函数为

fX(x|μ,σ)=

其中，x>0,μ>0,σ>0.分布的期望和方差分别为

Var(X)=(eσ2-1)e2μ+σ2.

而对索赔次数Y，本文初步假定服从某分布，如零截断泊松分布ZTP(λ)，其密度函数为

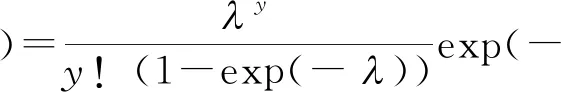
其中，y=1,2,…,λ>0.零截断泊松分布的期望和方差分别为

沿用文献[3,9]的做法，引入广义线性模型.设μi=h(xi)为对数正态分布的均值参数，λi=λ(xi)vi为零截断泊松分布的均值参数，i(i=1,2,…)表示第i个保单持有人，vi为第i个保单持有人的风险暴露量，对特征空间ri∈p,si∈q,定义回归函数h:X→+,λ:X→+,则

(2)

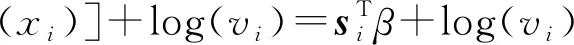
(3)

协变量矩阵ri和si在两个模型中可以不同.

所谓Copula回归模型,即基于一组协变量，将广义线性模型应用于边际分布的均值回归中，再用Copula函数对边际分布进行连接.

注意到在作者及相关文献中鲜有研究边际分布选择方法的报道，本文对此缺失进行补充，从而在客观上分别给出较为合适的索赔强度和索赔次数的拟合分布.具体做法有以下两点.

(1)回归变量的筛选

结合特征成分的相关性分析以及逐步回归法对回归变量进行筛选，根据AIC准则，选取关键的变量以减少模型的多重共线性.

(2)回归模型的选择

根据索赔强度和索赔次数各自分布的特点，本文分别考虑常用的几种分布来对回归模型(2)和(3)进行拟合.为了检验模型的预测性能，首先将数据集划分为两个集合：用D表示训练数据集(90%)、用T表示测试数据集(10%).

为了拟合单个模型，本文只使用训练数据集.通常情况下，这是通过最小化样本内损失(in-sample loss)来实现的.由于样本内损失容易过拟合，故本文综合计算测试数据集的样本外损失(out-of-sample loss)来进行模型比较和性能分析.样本内损失和样本外损失的明确定义见式(4)和式(5)[11].

(4)

(5)

最后，综合考虑AIC、样本内损失和样本外损失这三个统计量，确定索赔强度X和索赔次数Y的边际分布.

1.3 Copula函数的选择

在常用的阿基米德Copula函数中，Frank Copula的密度分布呈“U”字形，可以用于描述具有对称厚尾结构变量的耦合关系, 并且囊括正负相关结构.Frank Copula函数如下：

C(u,v|θ)=

(6)

1.4 保单总损失的分布[3]

由Sklar定理，索赔强度X和索赔次数Y的联合分布可以通过含有参数θ的Copula函数C(·,·|θ)来定义，即索赔强度和索赔次数(X,Y)的联合分布为

FX,Y|θ(x,y)=C(FX(x),FY(y)|θ)

(7)

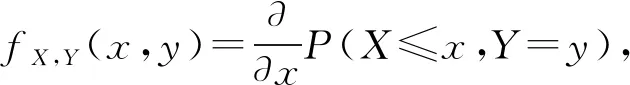
fX,Y(x,y|θ)=fX(x)(D1(FX(x),FY(y)|θ)-

D1(FX(x),FY(y-1)|θ))

(8)

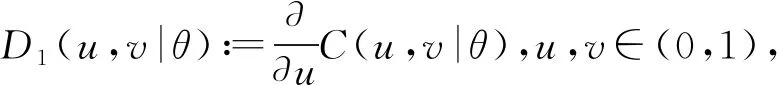
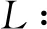
为简便，将二维随机变量记为(L,Y)T∈+×{1,2,…}.由X=L/Y得

(9)

对联合密度函数fL,Y(l,y)求L的边际分布函数,最终保单总损失的密度函数为

fL(l|μ,σ,λ,θ)=

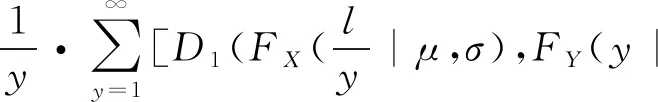
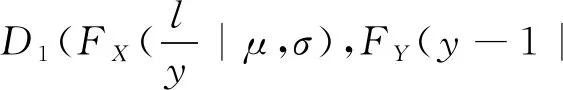
(10)

2 模型的参数估计[3]

(1)构造对数似然函数

(11)

这里x=(x1,…,xn)T∈n，y=(y1,…,yn)T∈n.

(2)极大化对数似然函数

极大似然估计量可以由下式给出:

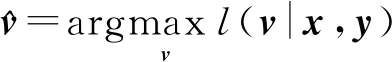
(12)

3 实证分析

3.1 数据描述

本文基于一组法国汽车第三者责任保险数据进行实证分析.该数据来源于R包CASdatasets中的freMTPL2freq和freMTPL2sev两个数据集，见文献[12].其主要收集了678 013份汽车第三者责任保单的风险特征(主要观察期为一年).由于本文对非零索赔的保单数据进行建模，所以首先根据保单ID将这两个数据集进行合并(此操作剔除了零索赔的保单数据)，合并后的数据集含有26 444份非零索赔的保单，每份保单含有13个变量，变量描述如表1所示.

表1 法国汽车第三者责任保险数据集变量

3.2 数据预处理[11]

首先，为保证模型的稳健性，将索赔金额大于10万的41份保单数据作为异常值删除，最终保留26 403份非零索赔保单数据.其次，由图2，索赔次数不小于4的保单数甚少，可以考虑将这些保单归为一类，即“索赔次数=4”这一类.图3提供了风险暴露量的柱状图，可以发现，许多风险暴露量小于1年，实际上只有54份保单的风险暴露量大于1年，最小值为1天.笔者认为所有观察结果都应在一个会计年度内，对超过一年的Exposure进行修正(将其设置为1).最后，本文根据图1对法国地区代号进行简化，例如用R24表示“Centre”，R93表示“Provence-Alpes-Cotes-D’Azur”.

图1 法国22个地区

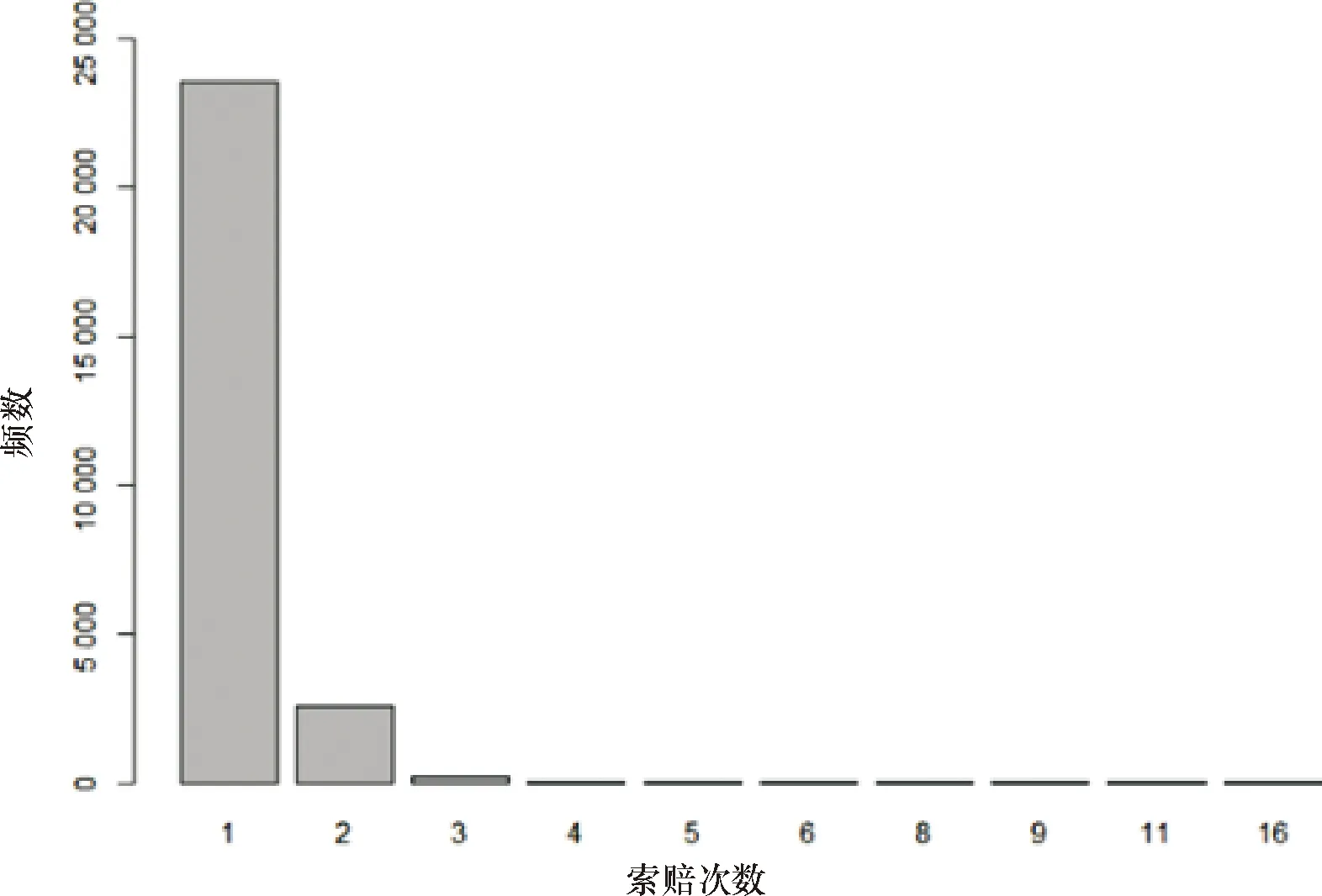
图2 索赔次数直方图

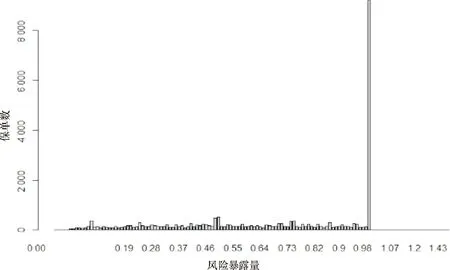
图3 风险暴露量柱状图

3.3 描述性分析

若不考虑协变量的影响，在索赔发生的条件下，索赔次数观察值与索赔强度观察值之间的Pearson相关系数为-0.058 5，Kendall秩相关系数为-0.206，Spearman等级相关系数为-0.248，相关性检验的P值都显著不为0.这就意味着，该组数据的索赔次数与索赔强度之间确实存在一定程度的负相关关系，但相关系数的绝对值较小.表2给出部分特征成分相应的Pearson相关系数和Spearman相关系数.该部分可为下文的变量选择提供参考.

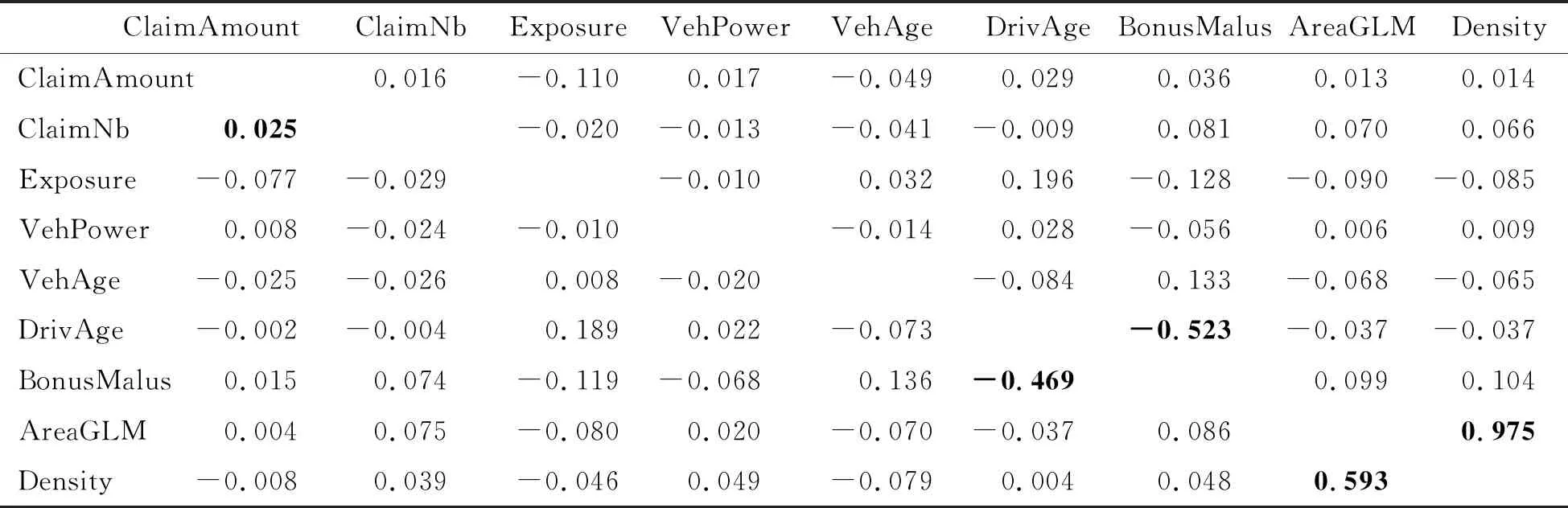
表2 数值特征成分的相关性*

3.4 边际分布的选择

(1)索赔次数

首先，用逐步回归的思想来挑选用于索赔次数拟合的变量.通过选择最小的AIC信息统计量，最终得到索赔次数的协变量:VehPowerGLM、VehAgeGLM、VehGas、Region、DrivAgeGLM、BonusMalusGLM、VehBrand和AreaGLM.

由于索赔次数是计数数据，因此，本文主要考虑常用的泊松分布、负二项分布、零截断泊松分布以及零截断负二项分布，分别对模型(5)进行拟合，拟合结果如表3所示.

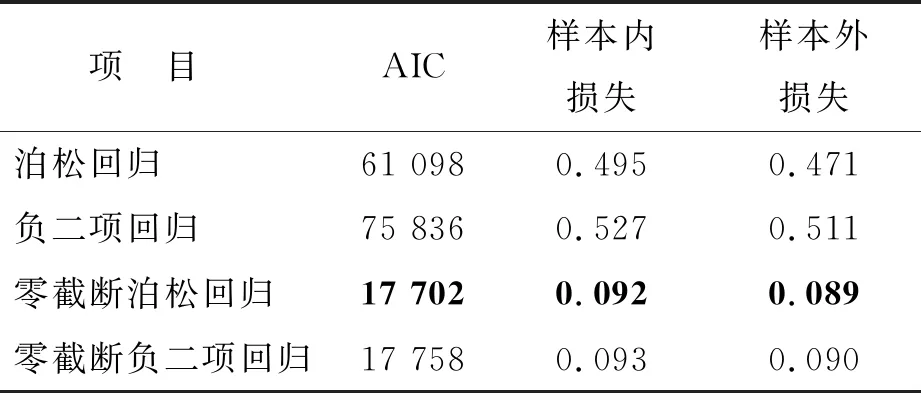
表3 不同分布假设的拟合结果

从表3中AIC及样本内、外损失三个统计量来看,零截断泊松分布对索赔次数的拟合效果最优.原因如下：

①该数据集只考虑非零索赔的保单，因此，索赔次数数据取值范围为正值，故从本质上讲采用零截断分布来拟合更合适.

②从E(ClaimNb)=1.122 5>var(ClaimNb)=0.142 32的角度看，该索赔次数数据不存在过离散现象，因此，使用零截断泊松分布的拟合效果略优于零截断负二项分布.

(2)索赔强度

同样地，用逐步回归的思想来挑选用于索赔强度拟合的变量.最终在所有变量的基础上剔除VehPowerGLM、AreaGLM及Region这三个变量.

图4的直方图描述了非零索赔保单在保险期间的索赔金额.为使图示更加清晰，该图仅呈现索赔金额小于15 000元的数据.可以看出，经验索赔金额呈现出明显的右偏特性.图5表明索赔金额的对数存在比较明显的对称特性.

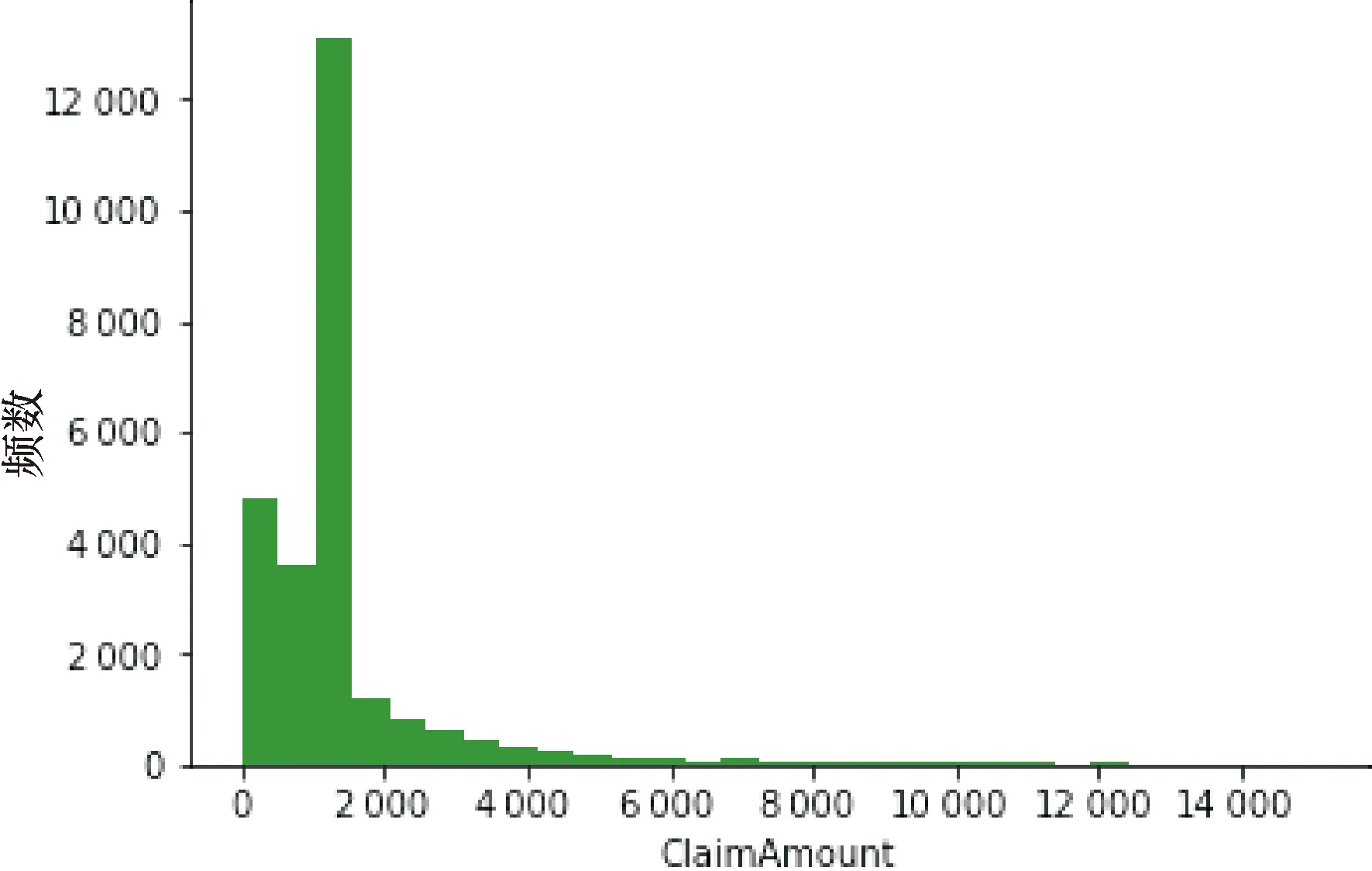
图4 索赔金额直方图

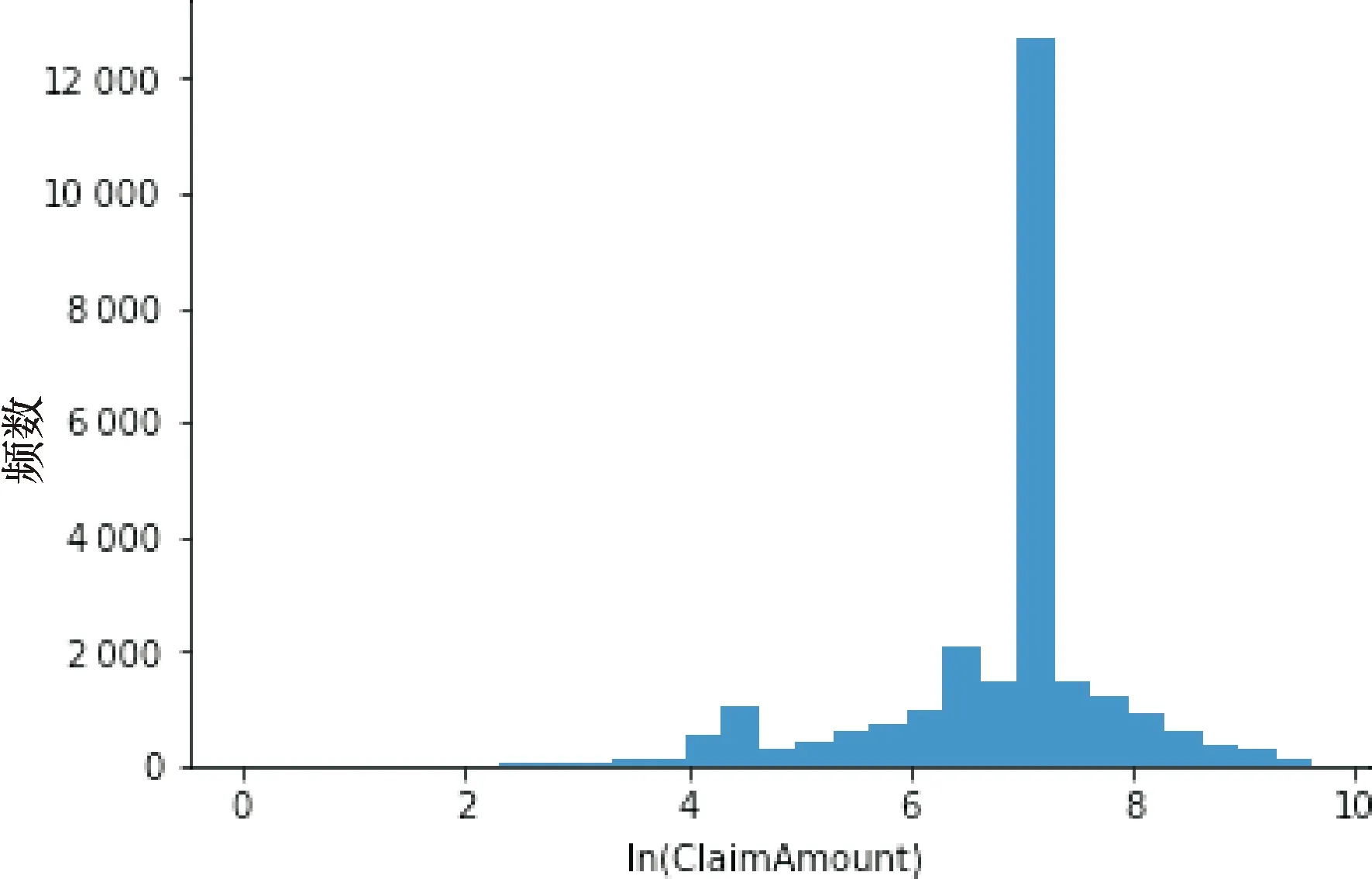
图5 对数索赔次数直方图

表4给出了非零索赔的26 403份保单索赔强度的描述性统计.该表显示，个体保单的平均索赔强度为1 599，观察到的最大索赔强度为96 422，该值远远大于所有个体保单索赔强度之和的0.01%.因此，索赔强度的分布初步判定为厚尾分布, 如伽马分布和对数正态分布.

表4 索赔强度的数字特征

不同分布假设的拟合结果见表5.

表5 不同分布假设的拟合结果

从表5的拟合结果来看，伽马分布的样本内损失略小于对数正态分布，但对数正态分布却在AIC及样本外损失这两个统计量上表现出对索赔强度较好的拟合效果.原因如下：

①无论是索赔金额(ClaimAmount)还是索赔强度(ClaimSize)，它们的直方图都呈现明显的右偏、尖峰厚尾的特性，对它们取对数后的直方图都较为对称.此外，本文计算得出的索赔强度的偏度和峰度分别为12.18和196.51，也佐证了右偏和尖峰厚尾的结论.

②资料显示，对数正态分布适用于右偏数据[13].因此，最终采用对数正态分布来拟合索赔强度数据.

至此，本文分别选取零截断泊松分布(ZTP)以及对数正态分布(LOGNO)为索赔次数和索赔强度的拟合边际分布.

3.5 保单总损失的拟合

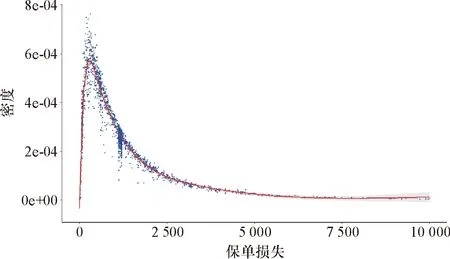
图6 ClaimNb=1时保单总损失的拟合分布

由图6可看出，保单总损失的拟合密度函数呈现右偏、尖峰厚尾的特点.这一结论与前文关于索赔强度的数据描述相吻合.为了更加直观地展示该拟合结果的准确性，本文选取了与图6来自同批数据的ClaimAmount变量作直方图，如图7所示.可以看出，两者具有一定的相似性：①两者都呈现右偏、尖峰厚尾的特点；②从拟合的密度函数来看，保单的总损失主要集中在[0，5 000]区间上，与图7的索赔总额区间大体一致.这在一定程度上体现了基于零截断泊松-对数正态分布的Frank Copula回归模型的总损失估计的准确性.特别指出的是，考虑索赔次数和索赔强度相依性的拟合密度函数对保单的总损失做出了较为保守的估计，这主要体现在拟合分布的尾部特征上.因此，有理由认为，考虑相依性的保单总损失Copula回归模型可以较为正确地评估汽车保险中某些从人、从车等风险，从而产生更为合理的保费评级，这也是对该数据集进行研究的初衷.

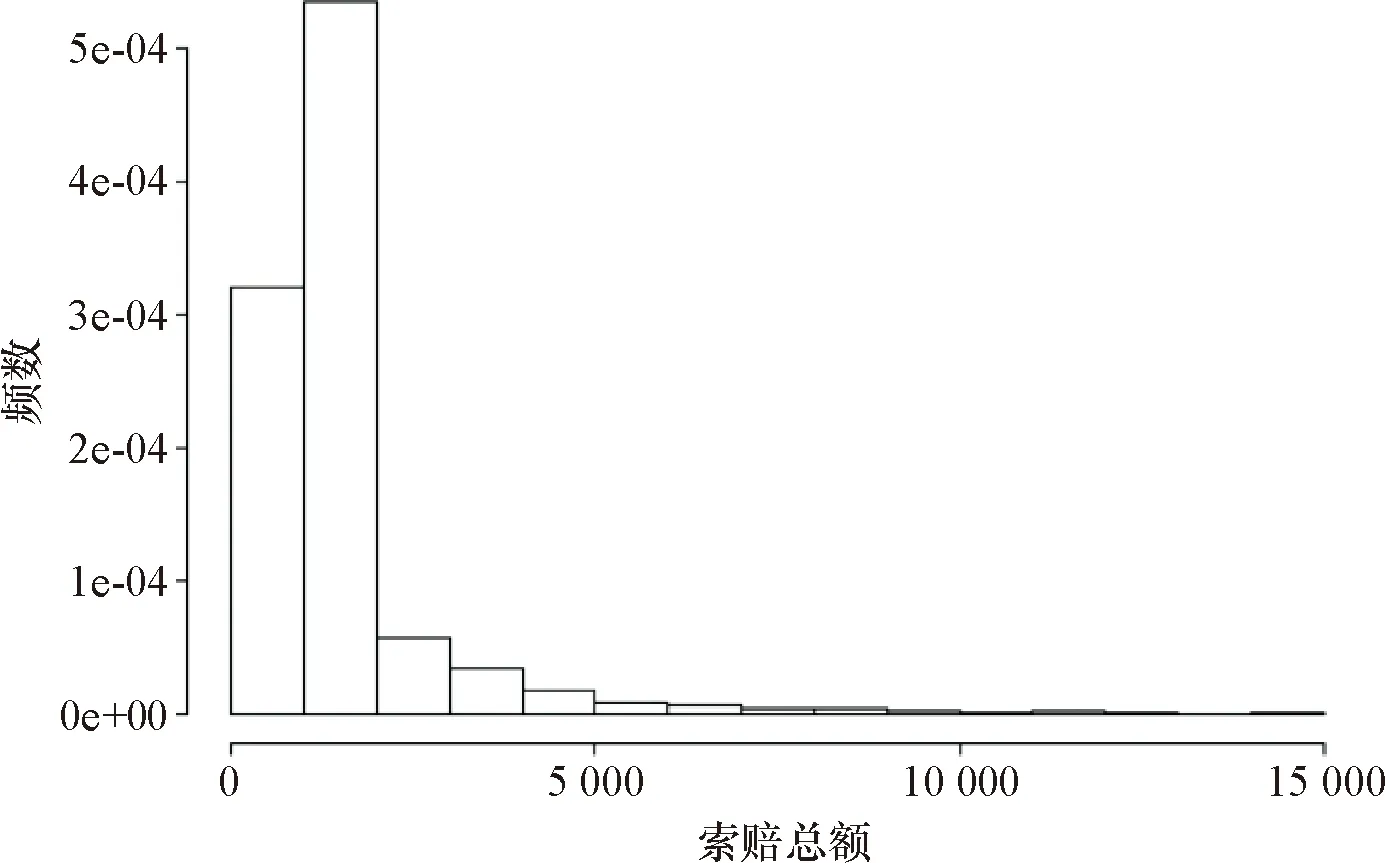
图7 索赔总额≤15 000的直方图

4 结 论

在非寿险损失预测模型中，传统的定价方法通常假定索赔次数和索赔强度相互独立.然而，本文从理论以及实证两个角度出发，推断出法国第三者责任保险数据中索赔次数与索赔强度存在一定的负相依关系.

基于Copula回归模型对保单总损失进行估计的方法其优势是能够将一些重要的风险管理信息考虑进模型中，且用一种灵活的相依结构来刻画变量间的相依性.本文主要从选取边际分布的角度出发，结合变量筛选和模型选择的相关方法对索赔次数和索赔强度的边际分布进行选取，并利用Frank Copula的特性对边际分布函数进行连接，最终给出保单总损失的拟合分布.

事实证明，考虑索赔强度与索赔次数客观边际分布及两者间相依结构特点的保单总损失估计模型将产生更为保守的保费，对保险公司制定合理的费率有一定的参考意义.这也是遵从精算谨慎原则,使保险公司减少遭受过大损失甚至破产的风险.