油相- 气相两相流对湿式离合器带排转矩影响的数值分析

成宵， 朱茂桃， 田乃利

(1.江苏大学 机械工程学院, 江苏 镇江 212013; 2.珠海华粤传动科技有限公司 南京研发部, 江苏 南京 211102)

0 引言

在车辆工作过程中，湿式离合器通过传递转矩来控制车辆的动力传输。由于离合器内部充满油液，使得摩擦组件在接合和断开过程中接触平稳，且油液能带走固体表面热量，改善摩擦组件的工作条件。但是，处于分离状态时，摩擦片和对偶钢片都以不同转速进行旋转，使得盘片间油液产生黏性剪切阻力，产生带排转矩[1-2]。带排转矩会造成功率损耗，增加离合器内部温度。因此，研究者正在努力减少带排转矩，以克服其造成的不良影响。

目前，国内外学者针对湿式离合器带排转矩进行了大量研究。陈炎云等[3]考虑润滑油的黏度- 温度特性，运用动网格技术模拟分析润滑油入口温度对湿式离合器带排转矩的影响，得到摩擦片表面压力、速度分布云图，但摩擦片边界定义为绝热边界条件，忽略了对流换热。熊钊等[4]基于有限体积法建立对偶片间油相- 气相两相流动模型，得出油液分布随沟槽分布呈周期性变化的结论，研究转速和沟槽数目对带排转矩的影响，认为增加沟槽数目可降低带排转矩最大值，但未考虑入口流量的影响。师路骐等[2]基于全转速下的间隙油膜动态变化情况，提出两种不同转速段下的带排转矩改进模型，研究偏置现象和油膜收缩现象对带排转矩的影响。林天昊[5]建立了大尺寸摩擦元件的油路模型，对比分析4种沟槽结构对带排转矩的影响，其中，径向油槽的带排转矩最小。但是，忽略了温度对油液的物理特性的影响，且沟槽结构形式不够完善。Kitabavashi等[6]提出了基于圆盘间隙层流的理论模型，假设在摩擦副间隙中润滑油始终处于全充液状态，体现了带排转矩在低转速期间随转速上升的现象。Kato等[7]提出由于气蚀的存在导致润滑液油膜发生破裂，利用湍流运动控制方程推导出间隙内油液流动压力分布，认为油膜破裂是从摩擦副内径处开始。但是，Yuan等[8]得出了相反的结论，考虑润滑油表面张力的影响，认为油膜破裂是由空化引起的外径处油液缺失，根据油膜等效外径的变化情况估算带排转矩。Iqbal等[9]基于纳维- 斯托克斯动量方程计算摩擦副间油液速度场和压力场，通过量化油液体积分数研究不同转速下流体特性，利用仿真和试验验证带排转矩的变化情况，但忽略了摩擦片表面油槽的影响。Yuan等[10]在有限元分析软件ANSYS/Fluent中建立二维摩擦副流场模型来模拟稳态两相层流流体状况，研究了钢片转速和旋转方向对片间油膜流动状况的影响，以及不同转速下气体与流体(简称气液)流动形势和气液交界面的变化情况。Neupert等[11]建立三维瞬态模型对比分析了径向槽和复合槽的油液流动情况，并使用高速摄像机记录试验过程中油气分布情况，但部分仿真数据与试验数据误差较大。

本文基于湿式离合器基本结构，建立了含径向槽的三维摩擦副流场模型，考虑了油、气混合分布对带排转矩的影响。基于不同转速下入口边界油液体积分数的变化情况，从两相流角度研究摩擦副表面油液占比和带排转矩随润滑油流量、摩擦副相对转速变化的情况，研究油气分布和带排转矩的关联性，并进行试验对比验证。研究沟槽旋向和角度大小对油液流动特性和带排转矩的影响规律，为优化设计湿式离合器系统提出研究方向。

1 数值方法

在进行计算之前，进行如下假设：

1)离合器内部各组摩擦副分离间隙相同；

2)润滑油流量均匀进入8对摩擦副中；

3)忽略钢片的外齿和摩擦片内齿等无关特征；

4)忽略重力影响；

5)不考虑温度、压力对油液物理特性的影响，比如黏度、密度等；

6)摩擦片转动，钢片固定。

1.1 物理模型

图1 湿式离合器结构简图Fig.1 Simplified structure of wet clutch

如图1所示，为湿式离合器结构简图。采用摩擦副内流域作为研究对象，即钢片中截面(垂直于旋转轴线)到相邻一侧的摩擦片中截面之间的油路区域，搭建摩擦副流体模型，如图2所示，其中：rf为摩擦副内半径，Rf为摩擦副外半径，rw为离合器内壳半径，Rw为离合器外壳半径，d为沟槽深度，w为沟槽宽度，δ为单对摩擦副间隙。将仿真模型分为入口流域、摩擦片附近油膜、钢片附近油膜、出口流域4个部分，其中：入口流域是附在离合器内壳体的油液层；摩擦片附近油膜是由沟槽中的油液和附在摩擦片表面的薄层油液组成；钢片附近油膜是附在钢片表面的薄层油液；出口流域是附在离合器外壳体上的油液层。摩擦副模型结构参数如表1所示。

图2 摩擦副流体模型Fig.2 Model of friction pair flow field

表1 摩擦副模型结构参数

Tab.1 Parameters of friction pair system

参数数值rf/mm70Rf/mm84rw/mm65Rw/mm90d/mm0.3参数数值w/mm1.5沟槽数目64δ/mm0.2摩擦副数8

1.2 周期性流场模型

如图3所示，建立含一个径向沟槽的周期性模型，采用旋转周期边界进行计算，降低计算所需资源。

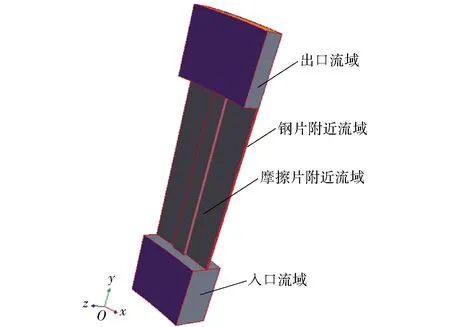
图3 摩擦副流场周期性模型Fig.3 Periodic flow field model of friction pair system

1.3 网格划分

采用多面体网格和棱柱层网格进行网格划分，分别选择4种不同的网格尺寸，进行网格独立性验证，如表2所示。由表2可知，随网格尺寸的减小，带排转矩的数值逐渐增大且变化率逐渐减小，即网格1和网格2的结果值接近。图4(a)和图4(b)分别为不同网格下的油液切向速度沿径向分布和油液体积分数沿周向分布的对比图。由图4可知，网格1和网格2的结果值相差不大，可认为基本尺寸低于2 mm的网格满足独立性。

表2 不同网格大小的模型对比

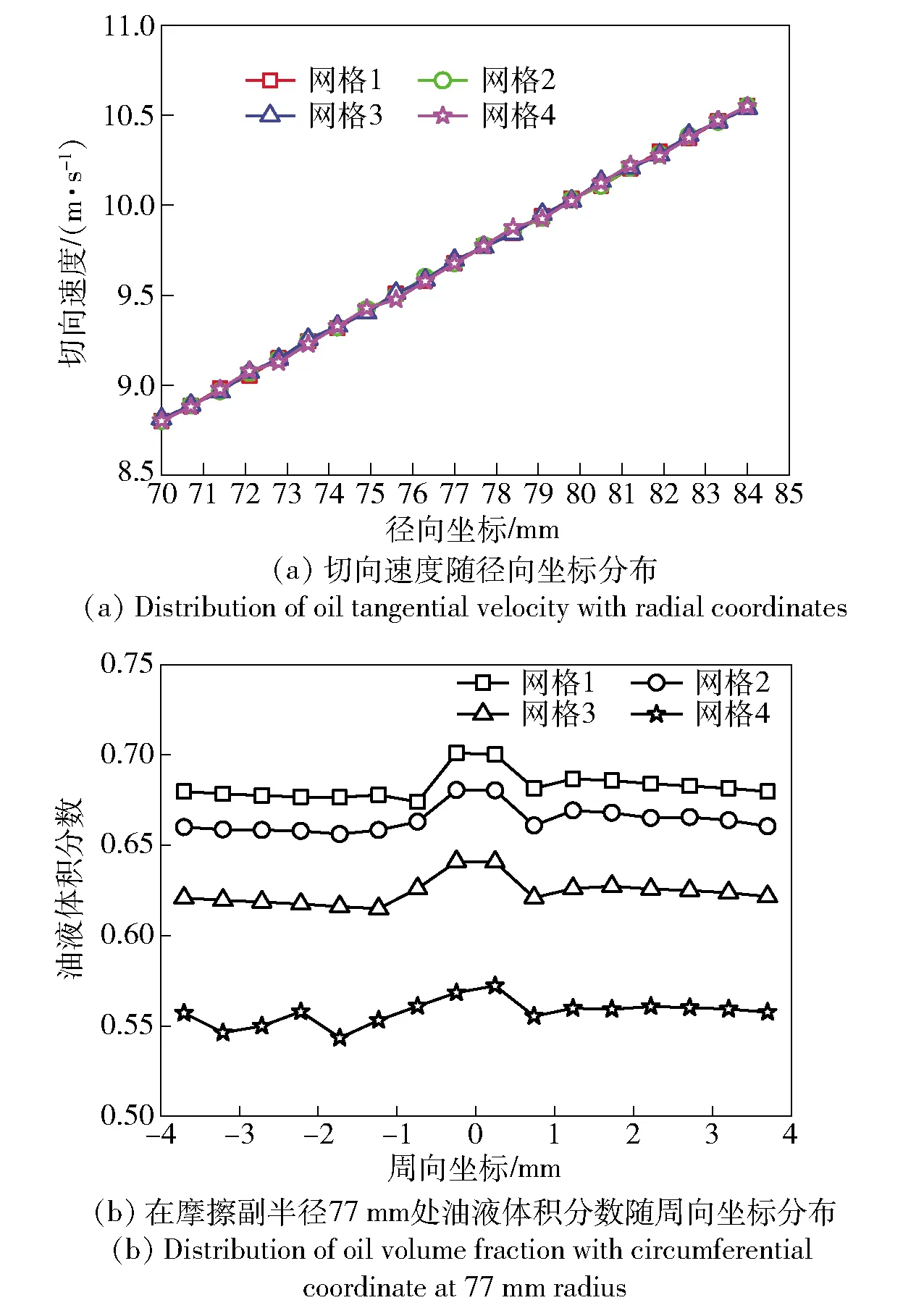
图4 不同网格尺寸的模型求解结果对比Fig.4 Comparison of computed results of different mesh size models

因此，选择基本尺寸2 mm的网格进行整体流域划分，再进行局部细化。通过体积控制指定间隙中油膜的基本单元尺寸为1 mm，并采用表面控制设置旋转壁面的目标表面尺寸为0.2 mm，总单元数为45 165，网格模型如图5所示。

图5 摩擦副流场网格模型Fig.5 Mesh medol of periodic flow field in friction pair

1.4 边界条件

基本边界条件设置如下：入口边界设置为质量流量进口；出口边界设置压力出口，以一个大气压作为环境压力；入口流域和出口流域中平行于Oxy平面的液体界面设置为对称面，其物理值使用重构梯度根据相邻网格单元推算得出；其余面设置为无滑移壁面。

针对运动边界，流体域中与摩擦片直接接触的壁面设置移动参考坐标系来模拟表面油液运动，其余壁面设置基准坐标系，表现为静止边界条件。

针对初始条件，需提供入口处的两相体积分数分布。根据Takagi等[12]提出该数值与摩擦副相对转速有关，其试验数据如图6所示。

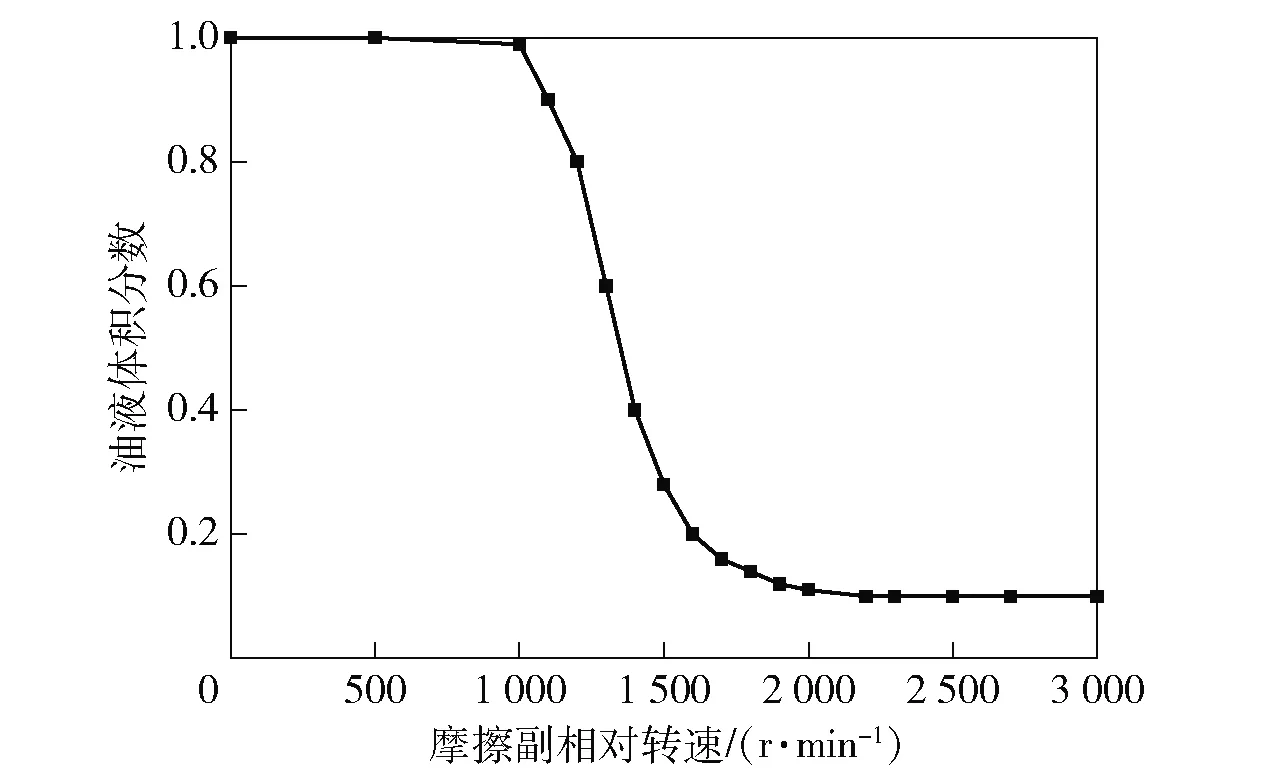
图6 入口处油液体积分数随转速变化[12]Fig.6 Chang of oil volume fraction with rotating speed at inlet[12]

1.5 计算方法

采用可实现k-ε两层湍流模型(k为湍流动能，ε为耗散率)和欧拉多相流模型下的流体体积函数(VOF)模型，进行稳态求解。欧拉相选择两相流，定义润滑油为主相，空气为次相。多相互动作用选择VOF-VOF相间相互作用模型和表面张力模型，使用某润滑油在35 ℃下物理特性参数，相关设置参数如表3所示。

表3 仿真模型参数

2 仿真结果分析与试验验证

2.1 油气分布与带排转矩

图7为不同转速下的油气分布图，图8为不同入口流量下摩擦片表面油液体积分数和带排转矩随转速的变化情况。

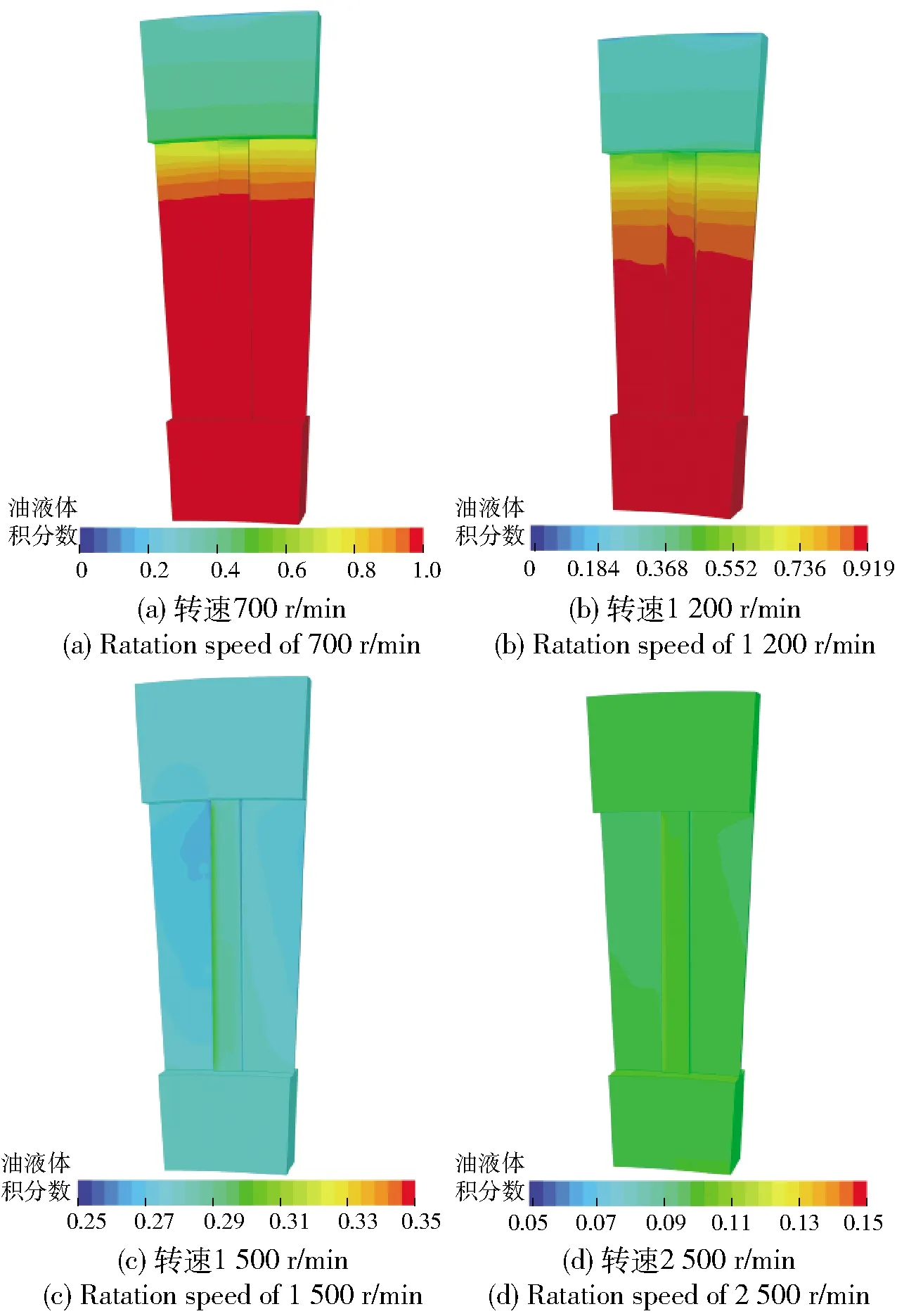
图7 入口流量7 L/min不同相对转速下油气分布云图Fig.7 Comparison of oil-air distributions with oil proportion isoline at various rotation speeds

图8 不同入口流量下油液占比和带排转矩的变化情况Fig.8 Oil volume fraction and drag torque at the surface of FP

不同入口流量变化趋势相同，油液体积分数随转速的增加而降低，但不同转速段变化速率不同。针对入口流量为7 L/min，当转速低于1 100 r/min时，定义为低速段，油液占比随转速下降缓慢到0.93. 由图7(a)可知，摩擦副片间流域充满油液，且油膜完好，空气主要存在于出口流域。油液体积分数等值线在摩擦片表面沿径向呈层状平行分布，越靠近出口处等值线数值变小。当相对转速范围是1 100～1 500 r/min，定义为中速段，油液占比急剧下降至0.16，中速段的下降速率是低速段的20倍。由图7(b)可知，空气主要由出口处进入片间流域，摩擦片表面油气分布呈现不均匀性。在相同半径下，摩擦片表面沟槽处与非沟槽域相比油液占比较高。当相对转速高于1 500 r/min时，定义为高速段，油液占比逐渐下降并趋于平缓，最后稳定在0.1. 由图7(c)、图7(d)可知，片间油膜被完全破坏，空气由入口和出口进入摩擦副间隙，间隙几乎被空气所占据，仅沟槽处存留油液，且油液分布在与转动方向相同的沟槽一侧。这是因为，附着在摩擦片壁面的油液满足无滑移边界。

另外，同一转速下油液体积分数随入口流量的增加而增加，油液占比出现陡降时对应的相对转速值越大。当入口流量为3 L/min时，最大油液占比变化率出现在1 200 r/min时，相比5 L/min数值降低了19.3%；当入口流量为7 L/min时，最大油液占比变化率出现在转速为1 300 r/min，相比5 L/min增加了25.8%. 入口流量对油液占比的影响主要出现在中速段，高速段入口流量对油液占比几乎没有影响。

针对不同入口流量，带排转矩随转速的变化趋势相同。针对入口流量为5 L/min，当转速低于1 100 r/min时，带排转矩的数值随转速呈正比增加，最大值为3.66 N·m； 随后，带排转矩迅速下降并趋于平缓，最小值为1.36 N·m；当转速高于2 200 r/min，带排转矩会有一个小幅回升阶段，增加至1.66 N·m. 另外，当入口流量降低至3 L/min，带排转矩最大值出现在转速1 000 r/min时，数值为3.07 N·m，相比5 L/min降低了16.12%. 当流量增加至7 L/min，带排转矩最大值对应转速为1 200 r/min，数值为4.63 N·m，相比5 L/min增加了26.50%. 带排转矩受入口流量的影响主要出现在中、高速段，低速段入口流量对带排转矩的影响不大。

因此，相对转速和油气分布对带排转矩的影响存在相关性。低速段时，因油液占比较高且变化不大，带排转矩只与转速正相关；中速段时，空气进入，油液接触面积减小，导致带排转矩迅速下降；高速段时，由于油液过少，产生的黏性剪切力较低，造成带排转矩较小且随转速变化不大。

2.2 试验验证

为了验证仿真结果，搭建了离合器带排转矩试验台架。试验中离合器为8组摩擦副，忽略各组间差异，将结果换算为单组摩擦副。由电机连接摩擦片端进行转动传递动力，制动器与钢片端连接使钢片固定。将摩擦片端转速从0 r/min逐步增加至2 500 r/min. 每隔200 r/min，设置该转速不变旋转5 s，以便在测量时得到稳定的带排扭矩值，记录该转速下的数值，取平均值。试验期间设置的物理参数如表4所示。

表4 试验条件参数值

图9所示为带排转矩的试验结果图，与图8(b)对比可知：仿真与试验的结果趋势相似，数值基本吻合。但是，在中速段时，仿真值比试验值偏高。这是因为，仿真模型结构简化导致油液流动条件更好，接触面增加，造成带排转矩值偏高。而处于高速段时，仿真值比试验值偏低，是因为此时仿真入口边界油液体积分数下降较快。同理，仿真中出现高转速区转矩回升现象，试验中未出现，是由于此时入口处油液占比变化不大，带排转矩仅与转速正相关，而试验中油液因转速升高仍在下降，造成带排转矩持续下降。

图9 台架试验下带排转矩的变化情况Fig.9 Measured drag torques on FP surface

如表5所示，不同入口流量下带排转矩最大值的试验值和仿真值的误差较小，验证了计算流体力学(CFD)仿真在摩擦副带排转矩计算中的正确性。

表5 带排转矩最大值比较

3 结构影响因素分析

改变沟槽的方向和角度γ，查看槽角对带排转矩的影响效果。保证入口流量为5 L/min不变的情况下，改变转速查看仿真结果。定义槽角倾斜角度与摩擦片旋转方向相反为正槽角，槽角倾斜角度相同为负槽角，如图10所示γ为正槽角。

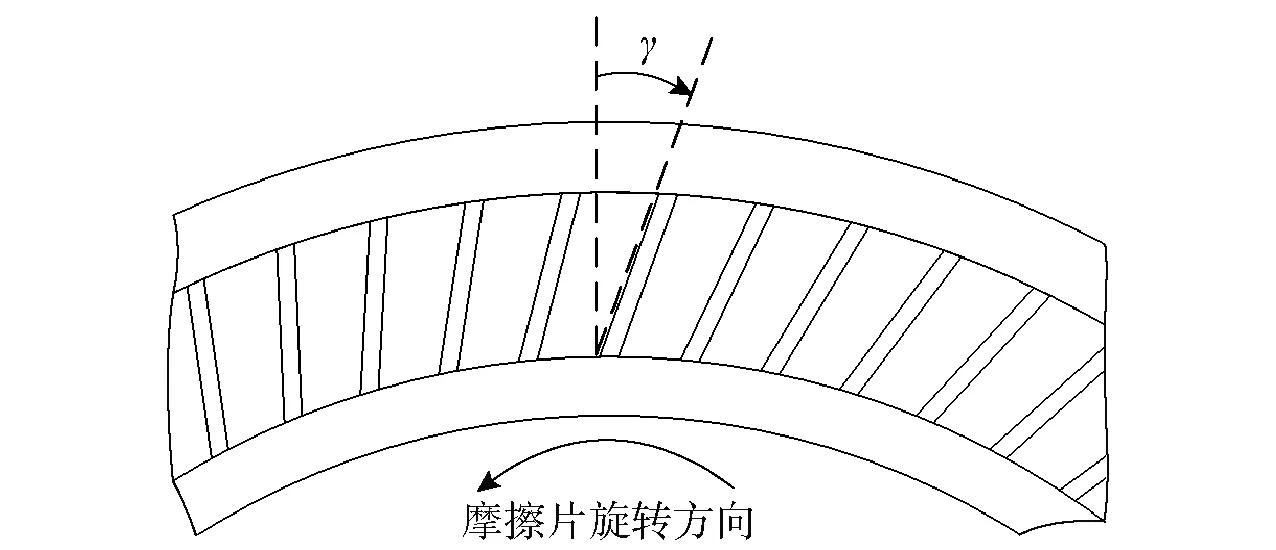
图10 摩擦副流场模型槽角示意图Fig.10 Positive groove angle on FP surface

如图11所示，不同槽角在1 200 r/min下的整体油气分布相似，油液占比等值线均呈层状平行分布，且随半径增大，数值逐渐减小。在同一半径处，油液更多集中在与旋转方向相同的沟槽侧面，即+x轴方向。但是，不同表面处油液流动存在差异。正向槽角的油液主要流经沟槽正面，沟槽+x轴方向侧面空气占比较大。而负向槽角情况相反，且负向沟槽入口处出现油液滞留区，油液占比较周围区域差异较大。因此，正向槽角的油膜连续性较好，油液更易进入沟槽中，而负向槽角油气混合情况更为复杂。同一半径处横截面A-A的油气分布更能体现该特点。负向槽角的沟槽两侧和片间间隙油液占比都较大，是因为油液随摩擦片转动时，负向槽角导致油液不易流通，易触及沟槽壁面而产生紊流，造成大部分油液滞留在沟槽两侧。

图11 不同槽角方向的沟槽在1 200 r/min下的油气分布云图Fig.11 Comparison of oil-air distributions with oil proportion isoline at 1 200 r/min in different directions of groove angle

如图12所示，不同槽角的摩擦片表面平均油液体积分数随相对转速的变化趋势相同，但同一转速下油液比存在差异。定义油液占比高于0.9时，摩擦副流场处于单相流转速区，其余为两相流转速区。单相流转速区时，与槽角0°相比，正向槽角油液占比高，负向槽角油液占比低，但差距不大。无论槽角方向如何，槽角增大油液占比增大。而在两相流转速区，槽角的存在均降低摩擦片表面油液占比。正向槽角的油液比高于负向槽角，且槽角越大、油液占比越小。另外，负向槽角进入两相流对应的转速低于正向槽角，优先进入两相流转速区。

图12 不同沟槽角摩擦片表面油液占比随转速变化Fig.12 Change of oil volume fraction on FP with various groove angles

槽角对油气分布影响在+x轴方向的槽角侧面更为明显(见图13)，不同槽角在该侧面随半径增大、油液体积分数逐渐减小。槽角0°的油液占比最大，且槽角角度越大，油液占比越小。正向槽角20°的油液占比最高为0.79，槽角增大20°，油液占比减少6.10%. 负向槽角20°的油液占比最大值与正向槽角20°相同，但不同半径处的数值偏高。当负向槽角为40°时，油液占比最大值比20°槽角降低16.46%，比40°槽角减少12.16%. 这是因为负向槽角过大时，油液流通性更差，整体流域油液占比更小，最大值仅为0.65.

图13 在1 200 r/min下不同沟槽角摩擦片的沟槽+x轴方向侧面油液体积分数沿径向分布情况Fig.13 Radial distribution of oil volume fraction on the +x side of groove on FP with various groove angles at 1 200 r/min

如图14所示：在单相流转速区内，槽角40°的摩擦片带排转矩最高，最大值为3.94 N·m. 将其余4种槽角的带排转矩最大值由高到低排列，槽角依次为20°、0°、-20°、-40°，且最大值数值比槽角40°分别降低9.14%、11.67%、19.54%、24.37%；在双相流转速区内，槽角0°的带排转矩最高，其余槽角的带排转矩较小。针对整个转速区，正向槽角的带排转矩高于负向槽角，20°槽角最大值为3.59 N·m，比0°槽角减少了1.94%，比-20°槽角增加了11.42%. 当正向槽角增加20°，带排转矩最大值增加9.75%. 与槽角0°相比，当负向槽角分别增加至20°、40°时，带排转矩最大值分别降低了9.98%、15.35%. 而正向槽角对降低带排转矩最大值的优势不大。因此，槽角的存在能有效降低两相流转速区的带排转矩，而负向槽角对于降低最大带排转矩有更大的优势。

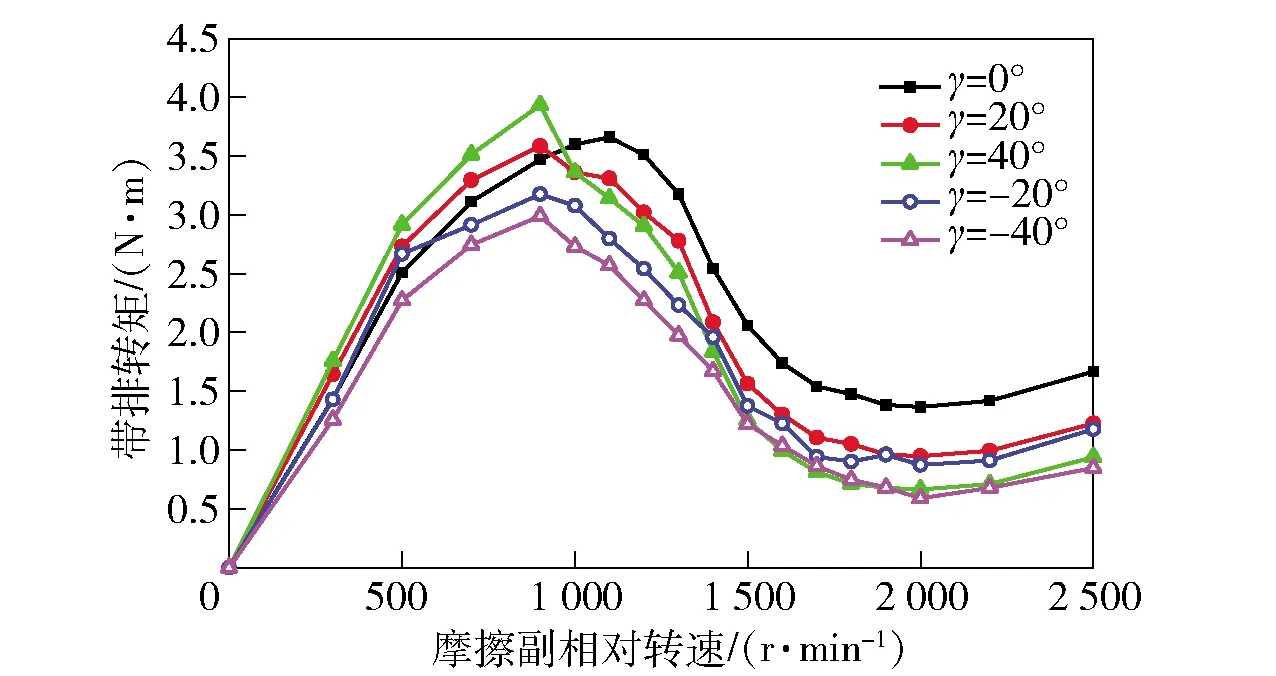
图14 不同沟槽角度摩擦片表面带排转矩随转速变化Fig.14 Changing curves of drag torque on FP surface at different groove angles

4 结论

本文采用数值计算和台架试验相结合的研究方法， 讨论了沟槽结构参数对湿式离合器带排转矩的影响规律。建立了含径向槽的摩擦副流体模型，研究了油气分布形式和带排转矩的相关性，获得了带排转矩随润滑油流量和摩擦副相对转速的变化规律。计算结果与试验数据基本吻合，验证了流体模型的正确性。得出以下主要结论：

1)单相流转速区，带排转矩随相对转速近似呈正比增加。当转速差达到某一值时，空气由出口和入口进入摩擦副间隙，流体表现为两相流形式，油气分布沿径向分层平行分布，且随转速增加油膜连续性越差，带排转矩达到最大值并随转速增加急剧下降，并趋于稳定。

2)油液流动情况与带排转矩的变化趋势相关。入口流量越大，同一转速下摩擦片表面油液占比越大，产生黏性转矩的表面面积越大，即带排转矩越大。入口流量的增加减缓了单相流向两相流过渡，造成带排转矩最大值对应的转速越大。

3)沟槽结构影响摩擦副表面油液附着情况，且不同旋向的槽角影响不同。单相流转速区，同向槽角对油液流动有促进作用，增加油液占比，增加带排转矩。负向槽角降低油液流动性，油液占比较小，减小带排转矩。两相流转速区，因槽角的存在均降低油膜连续性，增加油液滞留的可能性，降低带排转矩。