基于机车轮对的弹性复合圆柱滚子轴承深穴结构优化设计*

杨 文

（湖南铁道职业技术学院轨道交通装备智能制造学院 株洲 412001）

1 引言

随着高速、安全、舒适成为我国铁路运输的发展方向，其结构的安全性和可靠性成为研究的重点［1］。机车轮对是铁道机车车辆转向架重要的组成部分，其结构是否健康服役直接影响铁道机车车辆的运行安全性和可靠性。

1）相关科学问题

机车轮对是由车轮、车轴以及轴承等通过紧密配合而成的集成式功能部件［2］，在服役过程中，轨道车辆车厢负荷自上而下通过轴箱、轴承、车轴，再通过车轮传递到轨道。轴承在系统中起到传递和承担载荷的作用，各零件承受着复杂的弯曲、扭转复合载荷，成为轨道车辆轮对结构中受载频率最高、失效概率最大的部件。随着技术的不断进步，对机车轮对轴承的安全性和可靠性要求越来越高，而边缘应力集中导致滚动体两端以及滚道的两侧发生疲劳破坏，这种现象被称为“边缘效应”，这是机车轮对轴承的主要失效形式。

2）研究进展

（1）设计计算。业界学者对滚动轴承的“边缘效应”问题进行了大量的研究，主要是针对母线修型进行研究。1939年G.Lundberg通过对母线进行理论分析提出了著名的Lundberg凸度公式［3］。K.P.Singh和B.Paul提出了简单的离散化数值解法计算带凸度圆柱体的接触应力［4～5］。M.J.Hartnett提出了一种新方法针对滚动体表面的接触问题进行求解［6］。Kannel JW和HartnettM J［7］通过实验与理论相结合对滚动轴承的边缘区域应力的大小及分布进行了分析。De Mul JM和Kalker JJ［8］对滚动轴承的接触进行了分析，针对边缘应力分布以及弯曲应力有限区域进行研究。Reusner H［9］采取矩形单元的半无限条模型解法，该法不假设接触体为半无限体，将接触应力离散为若干矩形单元，而不假设接触半宽和最大接触应力成正比。通过对各种修形滚动体进行了分析，比较得出对数修形是解决边缘效应最佳方法。Hanson MT和Keer LM［10］对无摩擦的接触边缘效应进行了研究，对不同的楔角和弹性变量进行了讨论。Fujiwara H和Kawase T［11］通过数值方法对Lundberg函数修形的深入分析，并通过优化算法进行优化得出得出一组优化系数。NagataniH［12］以LP理论为基础通过对边缘应力的分析预测滚动轴承的疲劳寿命，并提出了相应的修正系数。L.Nayak和K.L.Johnson等的研究应归属矩形单元法［13］；R.Gohar等则采用三角形单元法［14～15］，它占据两个微段而沿轴向为等腰三角形分布，其优点是微段与微段之间相互重叠衔接，能组合成连续的接触应力分布，更易逼近载荷分布的实际情况，故计算精度较高。马家驹［16］运用J.Boussinesq半空间体力和变形的关系建立了有限长度线接触问题的力学求解方程，采用Ahmadi数值法求解了滚动体与滚道接触问题。陈晓阳［17］在马家驹的研究基础上，利用影响系数法对Lundberg对数修形的滚动体与内外圈滚道接触问题进行了研究，提出了相应在凸度设计方法。毛月新［18］通过增加凸度量的方法消除了倾斜的边缘效应，提高了滚动体轴承的抗偏斜能力，但没有对滚动体凸型进行设计。魏延刚等［19～20］采用有限元方法对滚动体与滚道在倾斜状态下的接触应力进行了计算，提出了滚动体非对称体修形概念。王世峰［21］等通过寿命对比试验对不同凸度的滚子进行了分析，结果表明对数母线滚子的寿命最高。王海亮［22］在接触分析的基础上针对圆柱滚子轴承的修形方式、凸度量大小以及滚动体修形之后对轴承的力学性能影响等方面做了研究。

（2）结构设计。在工程应用中，母线修型是解决“边缘效应”的一种主要途径。然而母线修型也存在着诸如修型曲线加工精度高，经修型的圆柱滚子轴承适合的载荷域较小等不足。魏延刚等［23～26］创新轴承结构，提出了深穴空心圆柱滚子轴承，并通过有限元分析表明深穴结构轴承可以避免或降低圆柱滚子轴承的边界应力集中；用实验证明了深穴滚子结构可以降低或避免滚子的接触“边缘效应”，但未见具体尺寸设计。徐弘毅等［27］通过显示仿真软件对滚子轴承进行数值分析，计算了不同变形本构关系材料模型的低速轴承在不同工况下的应力状况。Zupan等［28］将有限元技术引入装有轴承的机械结构的研究工作中并计算了结构的弹性矩阵以研究整体结构的变形。Bourdon等［29］建立了混合模型对静力作用下轴承进行研究。王超对不同凸形的高铁轴箱轴承接触问题进行了数值分析。

弹性复合圆柱滚子轴承是一种新型的滚动轴承［30～36］，见图1。通过对圆柱滚子轴承进行结构创新，在滚动体中嵌入高分子材料，使得滚动体弹性增强，与滚道接触面积增大，从而降低接触应力提升圆柱滚子轴承的承载性能，内嵌高分子材料的滚动体还具有减振降噪的物理性能［37～40］。理论研究表明，弹性复合圆柱滚动体边缘结构直接影响其边缘应力分布，合理的边缘结构设计可以有效降低或避免弹性复合圆柱滚子轴承“边缘效应”的存在。

图1 弹性复合圆柱滚子轴承实物图

在上述研究的基础上，基于机车轮对的工况对弹性复合圆柱滚子轴承的结构进行分析。首先针对弹性复合圆柱滚子轴承的机车轮对确定力学模型通过有限元方法确定机车轮对的工况，然后通过数值分析弹性复合圆柱滚动体边缘结构参数对边缘区域和椭圆区域的应力变化规律的影响，最后通过遗传算法对其参数进行优化。

2 力学模型

2.1 机车轮对力学分析

作为传动支承核心部件，轮对结构在高速运行机车上得到广泛运用，在运行中承受着各种复杂且随机的作用载荷。实践表明，在轮对结构设计中应主要考虑以下两种载荷：一种是超常载荷。在车辆使用寿命期中出现次数极小，甚至只有一次或数次，但其数值甚大的载荷，它为机车轮对的静态设计提供了载荷计算依据（包括垂直载荷、横向载荷和纵向载荷）；另一种是模拟运营载荷。构架上的大部分交变载荷，出现极为频繁、对使用寿命有着重要影响，它为转向架疲劳分析和疲劳试验提供了准静态和动态载荷值。本文主要考虑弹性复合圆柱滚子轴承对机车轮对结构超常载荷的影响，采取静态分析对力学模型进行重构，确定如图2所示机车轮对在服役工作中承载的力学模型。机车轮对通过两侧轴箱轴承座以及悬挂系统与转向架连接，承受整车车体及转向架的载荷，包括作用于轴箱轴承座的垂向载荷，横向载荷和纵向载荷，如图3所示。

图2 机车转向架轮对主要载荷示意图

图3 机车轮对力学模型

1）垂向载荷

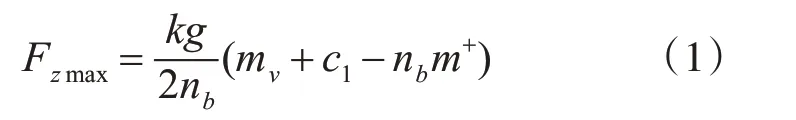
式中，Fz为构架超常垂向静载荷，N；mv为车辆的质量，kg；c1为旅客和行李的质量，kg；m+为转向架质量，kg；nb为转向架数；k为动荷系数，一般取1.4。

轮对轴颈载荷为

2）横向载荷

式中，nb为转向架数；ne为轮对数。

如果二系悬挂的横向刚度为K，横向止挡间隙为D，则二系悬挂所分得的载荷为

一个横向止挡所分得的载荷为

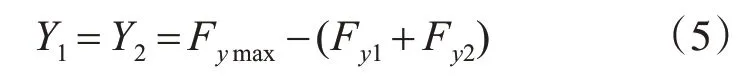
3）纵向载荷

在转向架构架上施加一个纵向牵引载荷，该载荷为

式中，kx一般取3。

2.2 弹性复合圆柱滚子轴承力学分析

圆柱滚子轴承在受载情况下，滚子与滚道受力线接触并变形。滚动体与滚道的接触是名义上的线接触，实际上由于滚动体长度小于滚道宽度，滚动体与滚道之间较大的接触应力集中在边缘接触区域和椭圆接触区域，如图4所示。普通圆柱滚子轴承边缘接触区域应力较大而形成“边缘效应”。

图4 线接触图

弹性复合圆柱滚动体如图5所示，L为滚动体长度，D为滚动体直径，d为材料填充直径，a为滚动体深穴角度，c为滚动体深穴半径。滚动体内嵌高分子材料其刚性较实心滚动体弱，更易发生形变，从而接触面积大，接触应力小。由于滚动体边缘有深穴结构设计较中间部位更易变形，其接触应力相应减低，从而有效降低或避免了“边缘效应”。

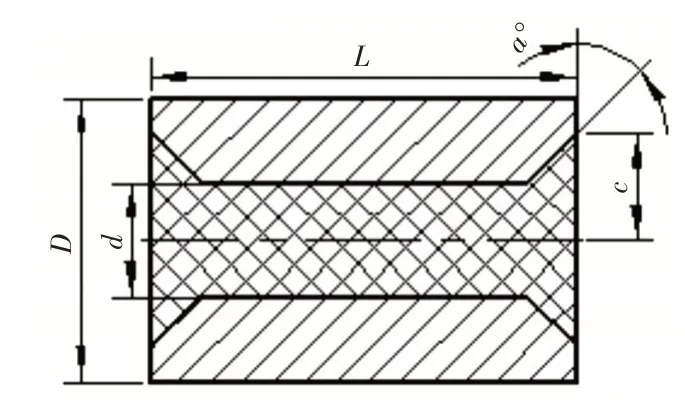
图5 弹性复合圆柱滚动体截面图

3 数值分析

应力集中是弹性力学中的一类问题，应力在固体局部区域内显著增高的现象。在应力集中区域，易使物体产生疲劳裂纹。“边缘效应”是一种典型的应力集中，直接影响着轴承的寿命。

机车轮对在工作中起到载荷传递的作用，运行中有着复杂的载荷。弹性复合圆柱滚子轴承具有较强的承载性能，应用于机车轮对中能承担复杂的载荷能力。复杂的载荷以及非线性结构在理论分析方面Hertz接触理论存在局限，本文借助有限元ABAQUS仿真软件对应用于机车轮对的弹性复合圆柱滚子轴承进行有限元建模和数值分析，并对深穴结构设计优化设计。

3.1 确定模型几何尺寸和材料特性

通过分析弹性复合圆柱滚子轴承的结构特点和服役特点，为了简化分析降低计算量，取弹性复合圆柱滚动体的部分和内外圈的部分作为分析模型，如图6所示。根据表1的材料参数对有限元模型进行材料属性定义。通过有限元计算，应用于机车轮对的弹性复合圆柱滚子轴承考虑其综合性能，其滚动体填充度（填充度K=d/D，D为滚动体直径，d为材料填充直径）取60%进行分析。

表1 遗传算法参数设置

图6 弹性复合圆柱滚子轴承有限元模型

3.2 定义边界和载荷

跟据弹性复合圆柱滚子轴承的工作服役特点，由于其高度对称特点，采用对称约束。整体边界条件的定义见表2。对轮对采取静态分析力学模型进行重构，主要包括垂直载荷、横向载荷和纵向载荷。通过式（1）～（6）进行理论计算得出作用于轴箱轴承座的垂直载荷、横向载荷和纵向载荷，将上述作用载荷加载于轴承上。

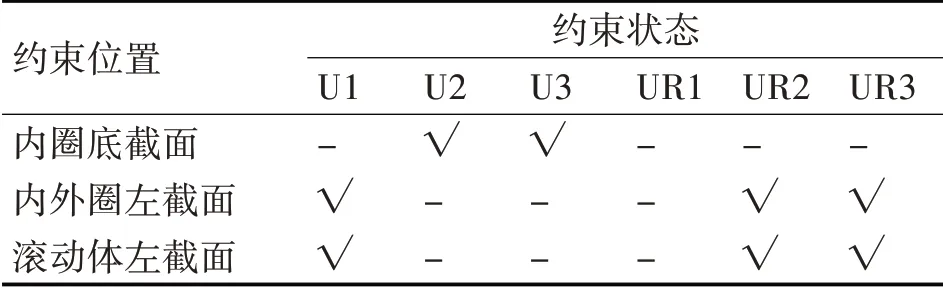
表2 约束情况

3.3 结果与分析

通过数值计算，弹性复合圆柱滚子轴承在机车轮对复杂的受载下，其最大应力均分布在滚动体上，且集中在椭圆接触区域和边缘接触区域。对滚动体最大接触应力和最大等效应力分布区域进行应力数值提取和分析，弹性复合圆柱滚动体的最大应力数值和分布区域随深穴半径和角度的变化规律，如图7及图8所示。

图7 弹性复合圆柱滚动体接触区最大接触应力图

据图7和图8分析，弹性复合圆柱滚动体接触区域最大应力呈现一定规律变化，边缘接触区域最大接触应力和等效应力随着深穴半径增大而降低，深穴角度越大其降低幅度越大；椭圆接触区域最大接触应力和等效应力随深穴半径增大而增大，深穴角度越大其增大幅度越大。在深穴半径和角度一定范围内，最大应力数值表明边缘区域存在应力集中，随着深穴半径和角度的增大，边缘效应明显降低，椭圆接触区域应力增大。

图8 弹性复合圆柱滚动体接触区最大等效应力图

4 结构优化

根据数值分析，结果表明最大接触应力和等效应力分布在滚动体边缘区域和椭圆区域。弹性复合圆柱滚子轴承在机车轮对复杂的受载下，为了增强弹性复合圆柱滚子轴承的承载能力，对滚动体结构进行优化，使弹性复合圆柱滚动体的边缘区域和椭圆区域的应力处于合理范围内，结合等效应力对疲劳破坏的影响，同时考虑接触应力与等效应力变化情况相似，仅针对等效应力进行优化，建立合理的数学优化模型是本优化的关键。

根据弹性复合圆柱滚动体的特殊结构形式，对结构优化的目标函数进行如下构造：

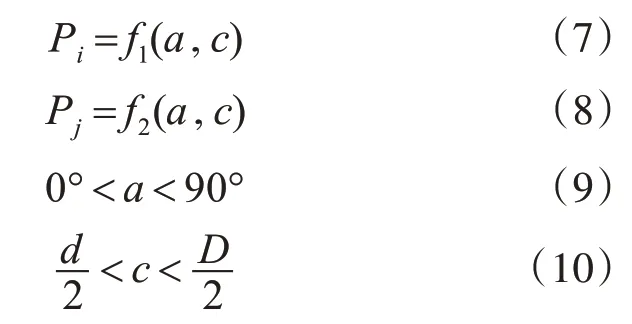
利用加权和的办法，将多目标问题转化为单目标优化问题，构造目标函数f：

式中，Pi和Pj分别为接触区域和椭圆区域的最大等效应力，m和n为加权系数。因此，弹性复合圆柱滚动体边缘结构优化归结为对参数a、c进行优化，通过遗传算法进行优化，得到目标函数f的最小值。遗传算法主要控制参数设定见表3。

表3 遗传算法参数设置

在迭代过程中，当运行至211代时，计算结果收敛，设计变量的优化后数值如表4所示。目标函数f=903.95MPa较优化前降低了4.3%，按加权值进行综合对比表明遗传算法优化的变量是最优解。

表4 优化前后比较

5 结语

1）弹性复合圆柱滚子轴承应用于机车轮对，通过对弹性复合圆柱滚动体的结构参数化，提出深穴角度a和深穴半径c两个参数，通过有限元分析，结果表明随着a和c的变化，弹性复合圆柱滚动体的接触区域接触应力和等效应力呈现一定规律变化。

2）通过数值分析与优化算法相结合对应用于机车轮对的弹性复合圆柱滚子轴承结构进行优化，得出最优结构尺寸α=58.14°，c=0.488Dmm，优化后的边缘效应得到了有效降低。