圆锥滚子轴承三线交点对其滑动摩擦的影响

潘隆，王金成，刘高杰，王朋伟

(1.洛阳LYC轴承有限公司，河南 洛阳 471039；2.航空精密轴承国家重点实验室，河南 洛阳 471039)

圆锥滚子轴承由于滚道对滚子的拖动力不足会出现打滑现象，打滑会使滚子与滚道之间的滑动摩擦加剧，产生过高的温升，进而导致轴承工作面烧伤或润滑剂失效等[1-3]。为实现滚子纯滚动，参考圆锥滚子轴承的设计方法[4]，一般将轴承三线(内、外圈滚道素线的延长线和滚子中心线)交点设计在轴承中心线上；但此方法仅能保证滚子在不受力状态下纯滚动，实际工作中轴承承受载荷时内、外圈会产生相对移动，三线交点会偏离轴承中心线，从而产生滑动摩擦。

在此建立圆锥滚子轴承力学平衡方程，分析轴向位移、径向位移和角位移引起轴承三线交点径向偏移量的变化，以及部分结构参数对轴承三线交点径向偏移量的影响，以此为基础对轴承进行优化设计，达到减小滑动摩擦的效果。

1 圆锥滚子轴承三线交点位置分析

圆锥滚子轴承滚子与套圈的几何关系如图1所示。在中、低速工况下，忽略运动的影响，可以采用静力学分析，将滚子和内圈当作内组件，内组件受外部径向载荷、轴向载荷及力矩载荷，外圈固定，并通过滚子与内组件产生接触载荷。

图1 圆锥滚子轴承滚子与套圈的几何关系示意图

每个滚子与外圈的接触载荷为

Qej=kneδ1.11，

(1)

δ=δrcosφjcosα+(δa+0.5Dpwθcosφj)sinα，

式中：kne为载荷-变形系数；δa，δr，θ分别为内圈相对外圈的轴向位移、径向位移、角位移；φj为第j个滚子方位角(第1滚子在径向载荷作用方向，方位角为0°)；Dpw为滚子组节圆直径；α为外滚道锥角。

内组件受力平衡方程为

(2)

式中：Fa为轴向载荷；Fr为径向载荷；Mm为外部力矩载荷；Qa，Qr分别为滚子与外圈的接触载荷在轴向和径向的分量;Z为滚子数量;Mme为接触载荷产生的抵抗力矩;Mmr为附加抵抗力矩。

(2)式是关于δa，δr，θ的非线性方程组，可参考文献[5]求解。

在外载荷作用下，滚子被压缩，三线交点由O移至O1，如图2所示。三线交点的轴向偏移量不会影响滚子纯滚动，仅需计算径向偏移量。

图2 在外载荷作用下轴承三线交点位置变化示意图

为简化计算，忽略内、外滚道主曲率，认为滚子夹在2个半空间之间[5]，内圈相对外圈的轴向位移和径向位移均由滚子变形引起。轴向位移会使滚子压缩变形，三线交点上移，每个滚子的三线交点径向偏移量相同。径向位移也会使承载区滚子压缩变形，三线交点上移，每个滚子的三线交点径向偏移量不同。角位移对处于对称位置的滚子影响相反，部分滚子三线交点上移，与之对称部分的滚子三线交点下移，偏移量相等。

根据几何关系可得轴向位移、径向位移和角位移引起的轴承三线交点径向偏移量分别为

(3)

(4)

(5)

式中：φ为滚子半锥角；β为内滚道锥角；De1近似取外滚道小端直径De。

2 结构参数对圆锥滚子轴承三线交点径向偏移量的影响

影响滚子与套圈位置关系的参数主要有外滚道锥角α、内滚道锥角β、滚子大端直径Dw、内滚道大端直径di、内圈大挡边宽度a0和外滚道小端直径De(图1)。

2.1 滚道锥角

其他参数不变，外滚道锥角α增大(减小)会使轴承三线交点上移(下移)，内滚道锥角β减小(增大)会使轴承三线交点上移(下移)，如图3所示，外、内滚道锥角变化引起的轴承三线交点径向偏移量分别为

(6)

(7)

式中：Δα，Δβ分别为外、内滚道锥角变化量。

2.2 滚子大端直径

其他参数不变，Dw增大(减小)会使三线交点下移(上移)，如图4所示，滚子大端直径变化量ΔDw引起的轴承三线交点径向偏移量为

(8)

2.3 内滚道大端直径

其他参数不变，di增大(减小)会使轴承三线交点上移(下移)，如图5所示，内滚道大端直径变化量Δdi引起的轴承三线交点径向偏移量为

图5 内滚道大端直径增大引起轴承三线交点上移示意图

(9)

2.4 内圈大挡边宽度

其他参数不变，a0增大(减小)会使轴承三线交点向左下(右上)偏移，如图6所示，轴承三线交点的径向偏移量与滚子径向位移相同，得到内圈大挡边宽度变化量Δa0引起的轴承三线交点径向偏移量为[6]

图6 内圈大挡边宽度增大引起轴承三线交点左下偏移示意图

δra0j=-Δa0cosβsinβ。

(10)

2.5 外滚道小端直径

其他参数不变，De减小或增大时轴承三线交点位置不变化，如图7所示。

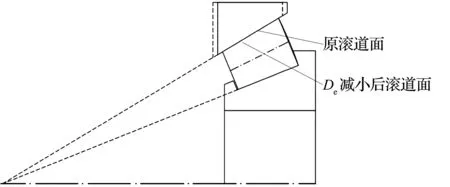
图7 外滚道小端直径减小时轴承三线交点位置示意图

3 基于纯滚动理论的圆锥滚子轴承优化设计

第j个滚子三线交点的理论径向偏移量为

δsrj=δraj+δrrj+δrθj+δrαj+δrβj+δrDwj+δrdij+δra0j。

(11)

用滚子与外圈的接触载荷与轴承三线交点偏移量乘积的绝对值来反映摩擦温升，即

(12)

轴承参数公差相对较小，对滚子与滚道的接触载荷的影响可忽略不计。每个滚子受力不同，三线交点径向偏移量也不同，调整轴承相关参数公差，可使部分滚子径向偏移量减小，部分滚子径向偏移量增大，但保证轴承M值最小,可减小摩擦温升。

Dw，di，a0，De是影响轴承装配高T的关键尺寸，调整公差时需复核，轴承装配高变化量为

ΔT=KgΔDw+KnΔdi+KaΔa0-KwΔDe,

(13)

式中：Kg，Kn，Ka，Kw分别为滚子大端直径、内滚道大端直径、内圈大挡边宽度、外滚道小端直径对轴承装配高的影响系数。

参考GB/T 307.1—2017《滚动轴承 向心轴承 产品几何技术规范(GPS)和公差值》可确定装配高的约束条件。

外、内滚道锥角与滚子半锥角的匹配性会影响轴承接触应力分布，一般设计为对称公差，为减小这2项参数对轴承三线交点的影响，在加工能力范围内应尽可能压缩其公差范围。为减小滚道的摩擦温升，可以通过调整Dw，di，De，a0使M值最小，同时要保证轴承装配高。优化设计流程如图8所示。

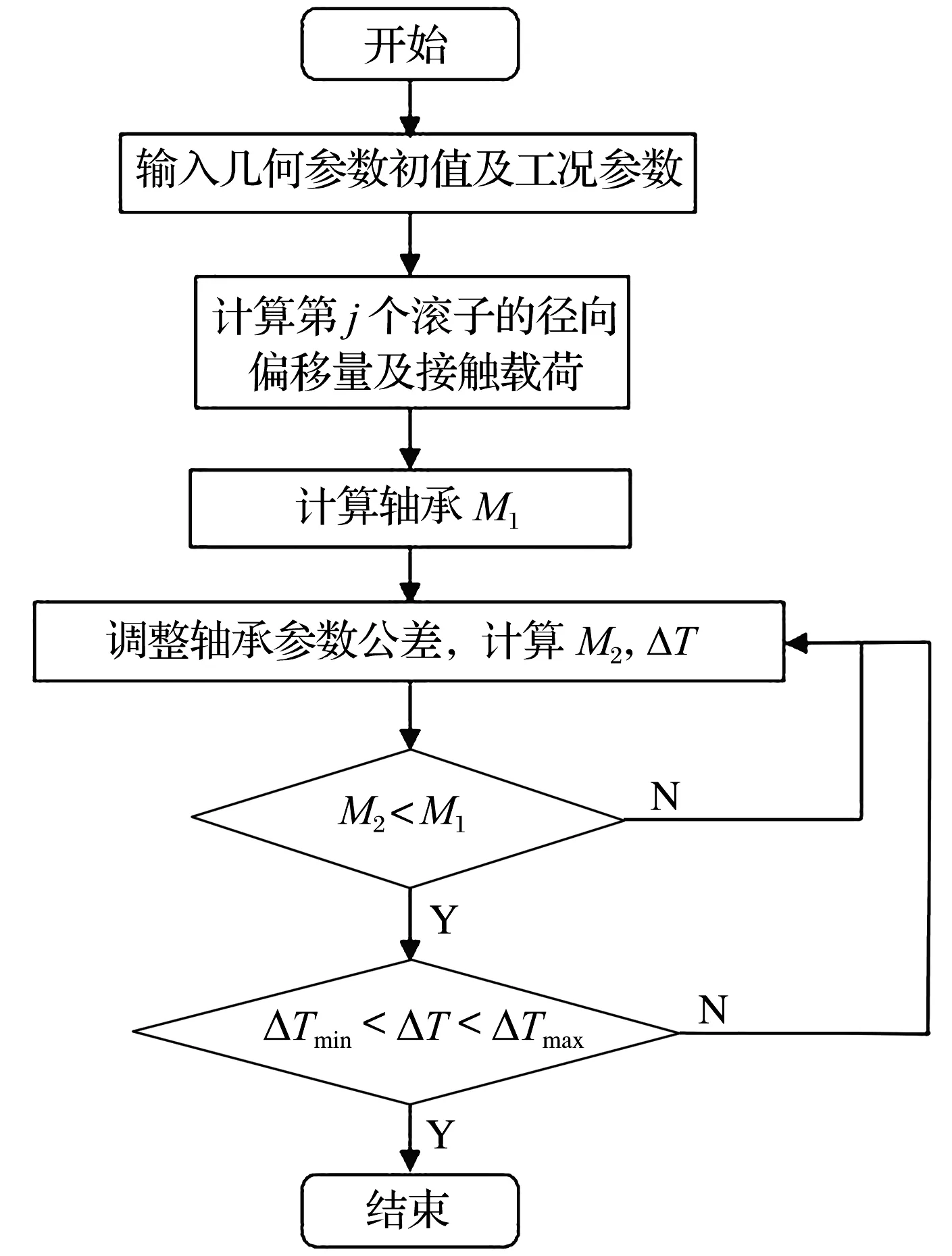
图8 优化设计流程图

4 实例分析

表1 30212E轴承主要结构参数

优化前、后轴承部分参数公差见表2，基于牛顿迭代法求解(2)式可得承载区各滚子接触载荷，再通过(3)～(12)式可得整套轴承M值，计算结果见表3，优化后轴承M值降低了42%，说明因轴承三线交点径向偏移引起的滑动摩擦大幅降低。

表2 优化前、后30212E轴承部分参数公差

表3 优化前、后30212E轴承承载区各滚子|Qejδsrj|值

5 结束语

在外载荷作用下轴承内、外圈会发生相对移动， 三线交点偏离轴承回转中心，滚子与套圈之间会产生滑动。本文分析了内、外圈相对位移及部分结构参数对轴承三线交点径向偏移量的影响，并以各滚子接触载荷与径向偏移量乘积的绝对值之和为目标函数，以轴承装配高为约束条件，对轴承优化设计，达到减小轴承滑动摩擦的目的。分析结果可为该类轴承的设计提供参考。