锥形避雷针避雷效果最优锥角研究

郭春轶 张雪华 杨林峰

(中原工学院理学院 ， 郑州 450007)



锥形避雷针避雷效果最优锥角研究

郭春轶 张雪华 杨林峰

(中原工学院理学院 ， 郑州 450007)

对圆锥形避雷针的锥角进行模拟计算，在已求得尖端面电荷分布密度的基础上，提出圆锥形避雷针模型在雷电防护中的锥角最优化理论。研究结果表明，高度确定的避雷针，在不同的云层电压下都存在一个避雷效果最好的锥角。

锥形避雷针；有效电荷；避雷效果；最优锥角

锥形避雷针避雷的最优化锥角问题一直是学术界的争论热点[1-2]。有学者认为，当避雷针的高度不变时，锥角越大，其有效表面积也越大，能够起到更好的避雷效果。另有学者认为，小锥角避雷针尖端聚集更多的电荷，会导致避雷针和云层间的空气更容易被击穿。本次研究将采用锥形避雷针模型进行理论模拟计算，讨论不同高度避雷针的最优锥角。

1 理论模型

建立一个圆锥形的避雷针模型，其中锥角为α，母线长度为r。 根据麦克斯韦方程组及Laplace方程，在导体边界条件下[3]，求出锥形导体表面的电势函数V，然后由电势函数V求出导体表面附近的电场强度E[4]，最后利用Gauss定理得到锥形导体的面电荷密度σ，表达式为：

(1)

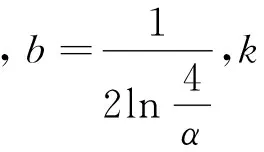
σ0=ε0·E=2.655×10-5(Cm2)

即避雷针中有效部分的面电荷密度为

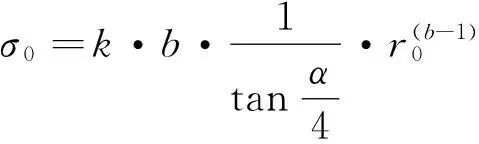
(2)

云层电荷电势为数十万伏到数千万伏之间，由此可判断k取值为10-7～ 10-5。同样进行积分，可得到避雷针表面电荷量：

(3)

当r=r0时，对应有效部分的电荷量为Q0。若整支避雷针对应的电荷量所产生的场强均能达到击穿场强，则r0为避雷针的母线总长。

2 理论计算结果

圆锥体的锥角采用弧度制，在r和k确定时，利用正交实验法依次计算有效电荷Q随锥角α的变化量。图1、图2、图3给出了模拟计算的结果。

图1 母线长度r =0.5 m的有效电荷量与锥角关系

图2 母线长度r =1.0 m的有效电荷量与锥角关系

图3 母线长度r=1.5 m的有效电荷量与锥角关系

数值结果表明，当锥形避雷针模型母线长度确定时，对应不同的云层电压常量，都存在一个避雷效果最优的锥角。图1、图2、图3分别给出的母线长度r为0.5、1.0、1.5 m时，k取不同值所对应的锥角。母线值确定后，随着k值的增大，避雷效果最好的锥角也在增大。

图1中，当k=1.0×10-6时，最优锥角α=1.59°；k=5.0×10-6，α=13.18°；k=9.0×10-6时曲线的峰值图中看不到，即对应的最优锥角在图像中未能显示，因为图中横轴的最大值为28.65°，显然最优锥角已经超过了这个值。

图2、图3显示的是当圆锥体模型的母线长r为1.0、1.5 m时，不同R值对应的最佳锥角。当k=1.0×10-6时，图2中α=0.74°，图3中α=0.47°;当k=5.0×10-6时，图2中α=5.73°，图3中α=3.81°；当k=9.0×10-6时，图2中α=13.47°，图3中α=8.02°。分析数据可以看出，保持云层电压常量k不变时，母线的长度增加，即避雷针高度增加，其所对应的避雷效果最优锥角减小。

避雷针锥角大小的选取需根据实际情况来定。

通常情况下不同地区在不同季节的雷电现象不同[5]，不同云层所带电位不同，各地区均有差异[6]。对k值进行了循环计算，得到确定高度的避雷针有效电荷量与锥角的关系(见图4)。

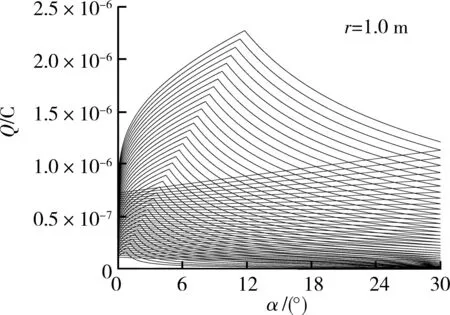
图4 对应避雷针有效电荷量与锥角的变化关系

图4显示，k值在1.0×10-6至9.0×10-6之间连续变化，峰值对应的锥角为0.74°到11.26°之间。因此，选取避雷针锥角时应该根据不同地区的情况而定。

3 结 语

本次研究对锥形避雷针防雷效果最好时所对应的锥角进行了数值模拟计算。数值模拟结果表明，在r取不同值时，对应不同的最优化锥角。锥体母线越短，避雷效果最优的锥角越大。这主要是因为母线长度确定时，云层电压常量k越大就要对应越高的击穿电压，这就需要避雷针携带有效电荷量增大。由面密度积分形式可知，此时避雷效果最好所对应的锥角应该增大。

[1] 张景昌.静电防护概论[M].北京：原子能出版社,2009：86-88.

[2] 刘尚和.静电放电及危害防护[M].北京：北京邮电大学出版社,2004:102-105 .

[3] GURU B S.电磁场与电磁波[M].周克定，译.北京:机械工业出版社，2006:99-103.

[4] 张云峰，王荣珠，蒲仕保.基于模拟电荷法分析避雷针线附近电位分布[J].微波学报，2015(1):18-22.

[5] 陈映洪.避雷针在广播电视发射台防雷技术中的应用分析[J].电子技术与软件工程，2016(8):23-26.

[6] COLEMAN B D.Lightning Rod Basics[J].Old House Journal,2016,44(2):52.

Research on Optimal Cone Angle for Protection Effect of Cone Lightning Rod

GUOChunyiZHANGXuehuaYANGLinfeng

(College of Science, Zhongyuan University of Technology, Zhengzhou 450007, China)

In this paper, the simulated calculation is performed over the angle of the cone lightning rod. On the basis of the acquired cone tip charge distribution density, the optimal angle theory is proposed about the lightning protection of the cone lightning rod model. The results show that the lightning rod with the fixed height bears the optimal angle of lightning protection as to various cloud voltage.

cone lightning rod; effective charge; lightning protection effect; optimal angle

2016-10-20

国家自然科学基金项目“一维金属纳米线电子稳定性的研究”(11547221)

郭春轶(1982 — )，男，河南镇平人，硕士，研究方向为凝聚态物理。

O441

A

1673-1980(2017)02-0113-02