不等高避雷针最小保护宽度计算方法研究
张 磊,章 鸣,石 磊,关均元
(1.衡水市气象局,河北 衡水 053000)(2.饶阳国家气候观象台,河北 衡水 053000)(3.河北雄安新区气象局,河北 雄安 071700)(4.中国雄安集团城市发展投资有限公司,河北 雄安 071700)
避雷针与地面连接,使云层内雷电能量导入地面[1],以此保障建筑物的安全。为降低雷电危害,优化避雷针导雷和保护性能尤为重要[2],因此需要对避雷针保护范围进行判断。
众多学者针对避雷针保护范围问题展开研究。万浩江等[3]提出避雷针吸收雷电评估方法,采用评估模型计算超高避雷针系统接闪效能的数值,得出结论:建筑物保护率随着接闪效果的增加而增大,避雷针上部接收雷电侧击的强度更大。该方法只能进行导雷效果判断,研究内容过于单一。周乾[4]对古建筑避雷进行研究,从绝缘材料方面讨论避雷针性能,对于影响避雷针性能的众多因素均未进行细致研究,无法判断避雷针保护范围。
为进一步优化避雷针导雷和保护性能,准确计算不等高避雷针最小保护宽度,以预留合适的保护裕度,提高不等高避雷针布阵效果,本文研究了不等高避雷针最小保护宽度计算方法。保护范围为避雷设备保护对象不受雷击的范围,将该范围细化为保护宽度。
1 坐标点与避雷针关系分析
根据几何原理,对单个避雷针保护半径ri进行计算,其表达式为:
(1)
式中:hi为接闪杆高度;hr为滚球空间球面半径;h为被保护物的高度。
根据电压保护规程[5]计算等高避雷针最小保护宽度。
1)采用避雷针(这里仅指单针)保护范围的计算方法计算两个等高避雷针外侧保护半径,分析单支避雷针折线法保护范围,进行保护范围校验,校验函数表达式为:
(2)

2)计算两等高避雷针最小保护高度h0,表达式为:
(3)
式中:D为两等高避雷针距离;m为两等高避雷针顶点和最小保护高度h0的联合保护宽度。
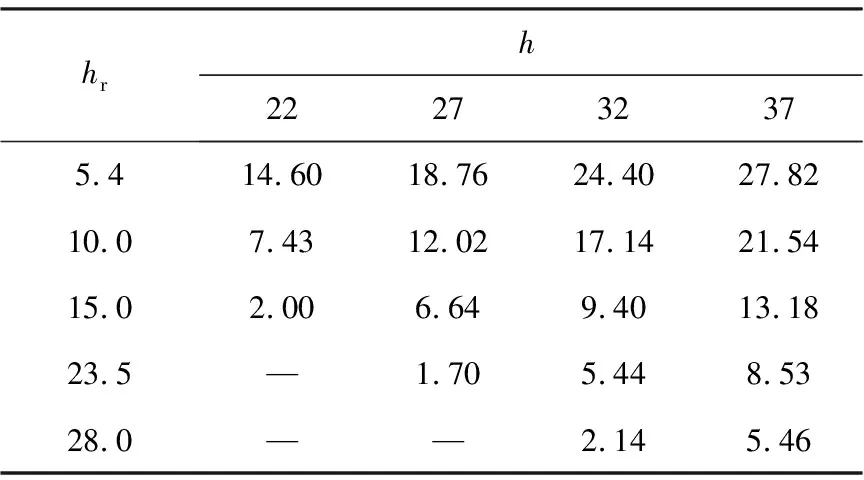
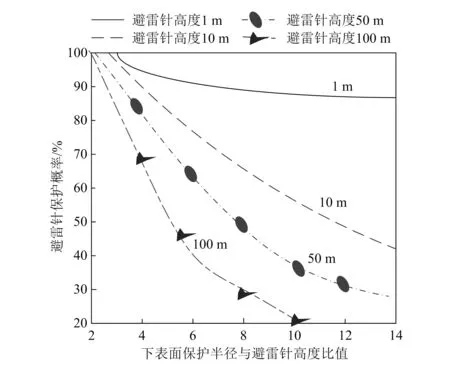
3)在接闪杆最高点所处平面内,通过两个避雷针的顶点和保护范围边缘的最低点形成弧线,确定保护范围,保护范围的一侧的最小宽度为保护宽度。对比h0与hi,若h0≥hi,则不等高避雷针都在最小保护宽度内;若h0 最小宽度bi为: (4) 通过单个避雷针保护半径确定多个避雷针保护面积。利用等高避雷针最小保护高度,确定3个不等高避雷针之间建筑的被保护高度,再通过滚球法计算不等高避雷针最小保护范围。为便于计算,构建空间直角坐标系,如图1所示。 图1 3个避雷针不等高保护范围的空间直角坐标图 设基准地平面为xOy,z轴垂直于该平面。设地面上有高度为z的一个避雷针,那么该针顶点坐标为(x,y,z)。 根据几何原理,已知3个点在滚球下表面内,可确定下表面上的一个圆;设置不等高避雷针数量为3个,其中任意2个避雷针的间距是Dij,3个避雷针顶点在滚球空间球面内的位置决定3个针内侧最小保护宽度,以此类推,将保护宽度直接定位到滚球半径上。滚球空间球面表达式为: (5) 式中:(x0,y0,z0)为滚球空间的球心坐标。 将3个避雷针的顶点坐标(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)代入式(5),则有: (6) 由于该方程组属于非线性方程,因此该方程组通过几何法求解。设置在半径为hr的滚球空间球面内,分布有3个避雷针的顶点,hr大于等于由3个顶点构成的独有圆的半径R,即: R≤hr (7) R=abc/ (8) (9) (10) (11) 为保证不等高避雷针布阵效果最佳,基于粒子群算法(PSO)优化避雷针最佳位置,精准获取最小保护宽度。优化过程如下: 1)设优化参数是不等高避雷针最小保护宽度,记作粒子维数,生成随机种群。 2)将避雷针保护能力作为优化目标建立适应度函数,以单个避雷针作为一个粒子,在多粒子群协同下,求解最佳位置与目标保护能力即期望值的误差,转换误差得到适应度,求解最优适应度。 对不等高避雷针布阵效果进行误差适应度运算,适应度函数表达式为: (12) 其中:nr为保护半径序号,r=1,2,…,N,N为被保护建筑高度;(xj,yj,zj)为被保护建筑的中心坐标,j=1,2,…,M,M为被保护建筑个数;g为常数。为防止避雷针保护方向受到影响,应用粒子群优化算法进行协同运算时,避雷针坐标取值需限制边界,约束条件为: nr=(xhr-xj)2+(yhr-yj)2+(zhr-zj)2 (R≤hr) (13) 将被保护建筑的中心坐标依次代入方程,结合避雷针顶点坐标,生成3个避雷针的内部保护范围。根据滚球法的定义,确定两个球面,保证以3个避雷针顶点所确定的圆为轴相互对称。 3)将遍历各个粒子获得的最佳避雷针位置和适应度进行对比,若适应度大于避雷针位置数据,则说明此适应度取值最佳,输出避雷针位置最佳值,将该结果保存。反之进入下一步。 4)不断更新粒子的速度与位置,直到适应度达到最优解,计算结束,获取保护能力最好的避雷针位置;反之,回到2)继续迭代。 计算不等高避雷针最小保护宽度,具体流程如图2所示。 图2 不等高避雷针最小保护宽度计算流程图 为测试本文方法性能,以河北衡水地区某通信站为实验对象,选取该通信站20组不同高度避雷针进行模拟实验,利用本文方法计算滚球空间球面半径hr与避雷针保护半径ri,计算结果见表1。 表1 滚球空间球面半径hr与避雷针保护半径ri 单位:m 根据表1可得保护半径ri为: (14) 通过保护半径可获得保护面积。当h为22 m、hi为5.4 m时,ri为14.60 m,保护面积是669.30 m2;当h为22 m、hi为15.0 m时,ri为2.00 m,保护面积是12.56 m2;当h为22 m、hi为23.5 m时,无法计算其保护半径。说明通过本文方法可判断被保护物体特质,便于预留合适的保护裕度。被保护高度不能高于避雷针高度,否则会造成保护失败现象。 为减少避雷针保护失败现象,利用本文方法计算避雷针高度、避雷针保护范围。随机选取该通信站4个不同高度的避雷针进行模拟实验,高度分别为1,10,50和100 m,可得避雷针保护概率如图3所示。 图3 避雷针保护概率 由图3可知,避雷针高度为1 m,其保护概率随着下表面保护半径和避雷针高度比值的增大而减小,但始终保持在88%~100%,避雷针保护概率比较平稳;避雷针高度为100 m,其保护概率一直呈下降趋势,可降至20%以下,说明此避雷针起到的保护作用较弱。 选取通信站某个避雷针,分析其保护效果。避雷针保护效果与雷电极的极性有关,雷电极对避雷针放电距离和雷电极对地面放电距离的比值为1时,避雷针保护效果如图4所示。 图4 避雷针保护效果分析 由图4可知,实线为避雷针的引雷分界线,虚线为被保护物的引雷分界线,它的上部空域都在避雷针的引雷分界线以内,M为被保护物体,雷电开始进入点是P,以P点为圆心,以hr为半径画圆,N为被保护建筑高度,经过H、M和地面3号点的分界线为被保护区域的引雷边界,这三点以下区域面积即单个避雷针的保护范围,此时避雷针能够吸收高于地面S距离的雷电,发挥保护功能。模拟结果与实际结果一致,说明本文方法可有效计算不等高避雷针最小保护宽度。 选取高度分别为25,40和55 m的3个避雷针,利用本文方法计算3个不等高避雷针最小保护宽度,设置被保护物体高度是10 m,将滚球下表面数据最低点与被保护物体的高度进行对比,结果如图5所示。 图5 不等高避雷针最小宽度保护区域 由图5可知,避雷针高度为55 m,滚球下表面数据最低点为21.86 m;避雷针高度为40 m,滚球下表面数据最低点为21.52 m;避雷针高度为25 m,滚球下表面数据最低点为20.28 m。利用本文方法,比较最低点与被保护物体高度可知,最低点均大于被保护物体高度,说明避雷针均在最小保护宽度内,最小保护范围由图5内黑色实线标出,但其中依旧存在无法保护区域,因为该区域不满足被保护物的高度要求,最低点小于被保护物体高度。说明本文方法可行性较高。 本文研究了不等高避雷针最小保护宽度计算方法。建立了不等高避雷针空间坐标系,创新性地利用滚球法计算避雷针保护半径;利用粒子群算法获取不等高避雷针最佳布阵优化结果,得出不等高避雷针最小保护宽度。实验结果表明,本文方法提升了避雷针应用效果,保证了不等高避雷针最小保护宽度符合实际测量值,减少了避雷针保护失败现象,提高了不等高避雷针实用性。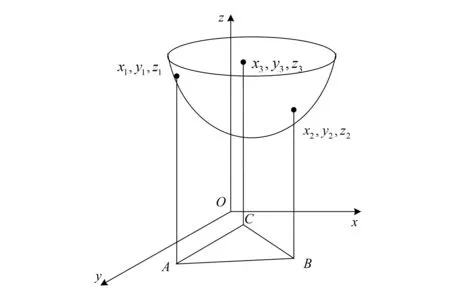
2 优化不等高避雷针布阵
3 最小保护宽度计算流程
4 实验


5 结束语

