基于最小二乘平差的全极化SAR配准偏移量估计方法

毛晓康，汪长城,周玉杉，王会强

(中南大学 地球科学与信息物理学院，湖南 长沙 410083)



基于最小二乘平差的全极化SAR配准偏移量估计方法

毛晓康，汪长城,周玉杉，王会强

(中南大学 地球科学与信息物理学院，湖南 长沙 410083)

全极化合成孔径雷达影像(PolSAR)相对单极化SAR影像有更加丰富的地表信息。为了提高SAR影像偏移量跟踪技术估算偏移量的精度，提出一种基于最小二乘平差法的全极化SAR数据偏移量估计方法。首先利用全极化SAR不同极化通道数据估算偏移量得到多个观测值，然后通过最小二乘平差法对多余观测值循环剔除粗差得到最优偏移量。文中选取美国科罗拉多州湖城(Lake city)区域的两景JPL无人机UAVSAR全极化SAR影像进行实验，结果表明，文中新方法具有良好的粗差探测和去除功能，相对于已有研究结果，在方位向和距离向的偏移量估算精度都有明显提高，达到15%～25%。新方法提高了偏移量跟踪估算偏移量的精度，这对利用偏移量跟踪技术监测滑坡、地震及冰川等有重要的意义。

全极化SAR；最小二乘平差法；偏移量跟踪；配准；粗差

合成孔径雷达(Synthetic Aperture Radar，SAR)图像之间利用偏移量跟踪技术来研究地物运动特性一直备受国内外学者青睐[1]。尤其在研究冰川、地震及滑坡运动特性，取得了较好的成果[2-3]。目前大多数研究都是利用单极化SAR影像估算形变偏移量，其中一些偏移量很难区分是粗差还是形变信息[4-5]。考虑到全极化SAR影像相对单极化SAR影像包含更丰富的地物散射信息[6]，在实际应用表现出很多优势。例如极化干涉测量(PolInSAR)就能被用来反演森林高度及林下地形[7]。因而在提高偏移量跟踪技术估算形变偏移量的精度有很大潜力需要去挖掘。综合上述两点，本文目的：①对比不同极化方式SAR偏移量结果；②利用全极化SAR影像来提高传统单极化SAR影像偏移量跟踪技术的精度，增强区分是否为形变信息的可靠性。

传统的SAR影像偏移量形变监测精度主要受影像空间分辨率与配准误差影响[8]。SAR影像空间分辨率是系统固有参数，难以通过数据处理手段提高。但配准误差可以在全极化SAR影像匹配中得到改善。不同极化电磁波与地物相互作用存在差异[9]，因此造成不同极化SAR影像配准误差不相同。本文首先利用全极化SAR数据分析不同极化方式SAR影像配准偏移量估算的相关性。然后利用不同极化SAR组合匹配估算偏移量产生多余观测值，提出基于最小二乘平差法的全极化SAR偏移量估算方法。最后选取覆盖美国科罗拉多州湖城的JPL无人机UAVSAR全极化SAR影像进行实验验证。

1 不同极化通道SAR偏移量相关性分析

PolSAR影像在地物的分类分割等相关领域已得到广泛应用[10]，主要是依据地表物体对不同极化方式电磁波的散射特性存在差异[6]。同一地物对不同极化电磁波反射能力有差异，在不同的地物类型、地表粗糙度及湿度等条件下也会有所不同[9]。为了分析不同极化SAR精配准后估算偏移量的相关性，本文设计了下面的实验。

选取间隔7 d获取的两景美国JPL高分辨率无人机UAVSAR全极化SAR影像。影像覆盖美国科罗拉多州湖城(Lake city)区域。截取影像中覆盖Lake city的一块区域进行实验，其SAR强度影像如图1所示。影像具体参数见表1。湖城位于美国克罗多河西南部圣胡安山脉下，北纬38°1′53″,西经107°18′53″，四周高山环绕。湖城建筑相对密集，对雷达的信号反射复杂，同时产生阴影也比较多。由于路面对雷达信号发生镜面反射，因此在SAR强度影像表现出较弱的信号。此外，SAR影像的噪声也比较严重，主要是来自SAR系统成像固有的斑点噪声[11]。SAR影像中的阴影和噪声等严重影响配准偏移量估算的精度[12-13]，甚至会引起粗差。

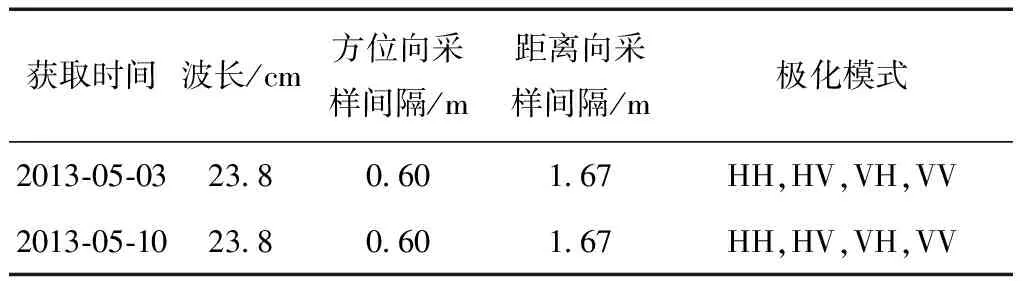
表1 JPL无人机UAVSAR全极化SAR影像具体参数

图1 2015-05-03获取的HH极化方式SAR强度图像及其地理位置图

利用传统的归一化交叉相关(Normalized Cross Correlation, NCC)匹配算法，分别对HH、HV和VV 3种极化SAR影像做精配准后估算偏移量，结果见图2。其中(a)、(b)和(c)分别代表SHH、SHV和SVV在方位向的偏移量，(d)、(e)和(f)分别表示SHH、SHV和SVV距离向的偏移量。由于影像覆盖区域为城区，且获取时间间隔短，因此在不考虑轨道误差的影响情况下可假设偏移量为零。本文选取偏移量绝对值大于3倍中误差视为粗差，可知图中不同极化得到的粗差区域有明显的差异。用皮尔逊相关系数分析[14]统计3种极化估算的偏移量之间的相关性。SHH与SHV在方位向偏移量相关值为0.24，距离向为0.19；SHH与SVV在方位向为0.42，距离向为0.46；SHV与SVV在方位向为0.25，距离向为0.28。它们之间的相关都未超过0.5，因此不同极化SAR影像估算的偏移量之间的相关性较小。

图2 不同极化方式SAR影像方位向和距离向偏移量估算结果比较

2 全极化SAR数据偏移量估算方法

2.1 单极化SAR数据偏移量估算算法

偏移量跟踪技术首先利用两景相关的影像中的像元进行精配准，得到两景影像配准同名像元的坐标偏移量。坐标偏移量中包含：①地形起伏，电离层等因素引起的偏移量；②获取影像的轨道差异引起的偏移量；③地表形变引起的偏移量。由地形起伏引起的偏移量在基线较短和地形相对平坦的时候很小[15]，一般忽略不计。考虑机载无人机平台低空飞行，因而不考虑电离层、大气等因素引起的偏移量。因此坐标偏移量Roffset就等于轨道偏移量Rorbit和形变偏移量Rchange之和。

Roffset=Rorbit+Rchange.

(1)

由于影像中绝大部分地表处于稳定状态，其理论偏移量为零，但是在实际应用中受到轨道偏移量的影响而与理论值产生偏离。因此可以利用稳定区域的偏移量来近似估计轨道引起的偏移量，即假设Roffset≈Rorbit。一般情况下，采用二次方程来建立轨道偏移量模型，并利用最小二乘方法拟合模型参数。

Rorbit=a0+a1·l+a2·p+a3·l·p.

(2)

其中:a0,a1,a2,a3为待定系数；l,p分别代表像元在SAR影像中的行列数,行代表方位向，列代表距离向。在实验过程中，利用最小二乘法对模型参数进行拟合(采样点为2 000)，模型的内符合精度一般作为评价偏移量精度的一个指标。

对于坐标偏移量的计算，核心是寻找主从影像同名像点。寻找同名像点的算法有很多，一般利用基于强度信息的相关系数法。相关系数计算公式如下[16]：

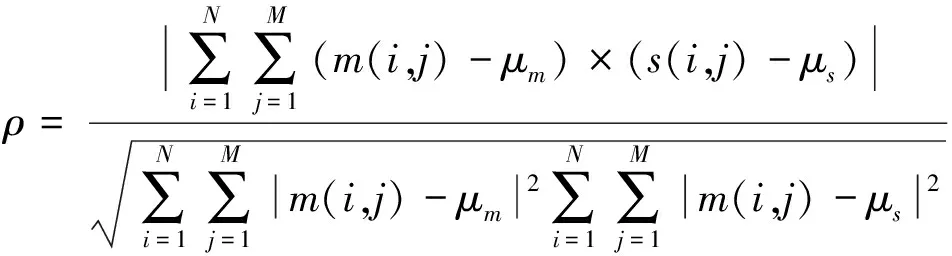
(3)

当相关系数取得最大值时的位置为最佳匹配点。主从影像的同名像点的位置用slave(l′,p′),master(l,p)表示，按式(4)计算偏移量。

Rorbit=slave(l′,p′)-master(l,p).

(4)

2.2 全极化SAR数据偏移量估算方法

(5)

(BTPB)X=BTPL.

(6)

解得

X=(BTPB)-1BTPL.

(7)

X的中误差为

(8)

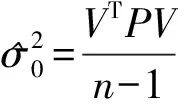
3 实验验证

为了验证本文算法，利用图1对应的两景JPL无人机UAVSAR全极化SAR影像进行实验。方位向和距离向的偏移量估算结果如图3、图4所示。图3(a)～(f)分别为SHH，SHV，SVV，SHH+SVV，SHH+SHV+SVH+SVV及平差方法得到的方位向偏移量估算结果。图4(a)～(f)分别为上述方法在距离向偏移量估算结果。从图3和图4可以看出，本文提出的方法的结果(图3(f)和图4(f))中偏移量粗差明显少于单极化SAR影像估算结果，尤其是在距离向比较明显(见图4中的黑色圆框所示区域)。

图3 不同组合方位向形变偏移量

图4 不同组合的距离向偏移量

另外，为了分析不同的匹配窗口大小对结果的影响，分别利用4种不同大小的匹配窗口64×32(方位向×距离向)、96×48、128×64及160×80进行实验验证。统计不同方法在不同大小匹配窗口条件下的偏移量估算结果的中误差，结果如表2所示。从表2可知，随着窗口增大，不同方法在方位向及距离向偏移量估算精度均随之提高，然而结果的细节信息会随着匹配窗口的增大而损失；本文方法相对单极化SAR结果在不同的匹配窗口条件下精度均提高15%～25%，且在匹配窗口较小时精度改善更为明显。

表2 不同极化组合偏移量中误差

本文方法利用小的匹配窗口估算偏移量精度与单极化SAR利用大的匹配窗口估算偏移量的精度相当。例如本文方法选择96×48的匹配窗口偏移量精度：方位向5.654 0 cm；距离向1.990 4 cm。传统单极化SAR只能选择128×64的匹配窗口才能达到与本文方法相近的精度，方位向5.615 4 cm；距离向1.959 5 cm。同理其他窗口也有类似规律。详见表2中虚线框和实线框分别对应的结果。

4 结 论

1)利用偏移量跟踪算法处理不同极化方式SAR影像，估算的偏移量存在差异，尤其是粗差区域更明显。用皮尔逊相关系数分析得它们之间偏移量的相关性都在0.5以下。

2)利用本文提出的基于最小二乘平差的全极化SAR配准偏移量估计方法，处理高分辨率全极化机载SAR数据。结果表明，本文方法能够较好地剔除单极化SAR估算偏移量中的粗差。对比传统单极化SAR处理的结果，本文方法偏移量估计精度提高了15%～25%。

3)比较不同大小的匹配窗口估算偏移量，本文方法对比传统方法，精度均得到提高，且在匹配窗口较小时精度改善更为明显。传统方法一般通过增大匹配窗口大小，提高偏移量估算精度，而本文方法利用小的匹配窗口(96×48)估算的精度与传统方法选择大的匹配窗口(128×64)的精度相当。因此，本文方法在保证精度不变的情况下，能降低匹配窗口的大小，不仅减少大量的计算，而且还能保留更多细节信息。

[1] STROZZI T, LUCKMAN A, MURRAY T, et al. Glacier motion estimation using SAR offset-tracking procedures[J]. Geoscience and Remote Sensing, IEEE Transactions on. 2002,40(11): 2384-91.

[2] 李佳，李志伟，汪长城，等．SAR偏移量跟踪技术估计天山南依内里切克冰川运动[J]．地球物理学报，2013，56(4)：1226-1236.

[3] HU J, LI Z W, DING X L, et al. Two-dimensional co-seismic surface displacements field of the Chi-Chi earthquake inferred from SAR image matching[J]. Sensors. 2008, 21;8(10):6484-95.

[5] SINGLETON A, LI Z, HOEY T, et al. Evaluating sub-pixel offset techniques as an alternative to D-InSAR for monitoring episodic landslide movements in vegetated terrain[J]. Remote Sensing of Environment. 2014,5;147:133-44.

[6] ZEBKER H. Polarisation: Applications in Remote Sensing[J]. Physics Today. 2010,1;63(10):53-4.

[7] 付海强, 汪长城, 朱建军，等. 一种改进的PolInSAR PCT方法反演植被垂直结构[J]. 测绘工程, 2014,23(11):56-61.

[8] 陈强,罗容,杨莹辉,等.利用SAR影像配准偏移量提取地表形变的方法与误差分析[J].测绘学报, 2015,44(3):301-308.

[9] 王超.全极化合成孔径雷达图像处理[M].北京：科学出版社, 2008.

[10] 王兴玲,胡德勇,唐宏, 等. 基于Bayes决策的机载全极化SAR图像滑坡信息提取[J].国土资源遥感, 2014,26(2):121-127.

[11] LEE J S, POTTIER E. Polarimetric radar imaging: from basics to applications[M]. CRC press, 2009.

[12] 刘国祥,丁晓利,李志林, 等.星载SAR复数图像的配准[J].测绘学报, 2001,30(1):60-66.

[13] ZITOVA B, FLUSSER J. Image registration methods: a survey [J]. Image and vision computing, 2003,21(11):977-1000.

[14] DUTILLEUL P, STOCKWELL J D, FRIGON D. The Mantel Test versus Pearson's Correlation Analysis: Assessment of the Differences for Biological and Environmental Studies[J]. Journal of Agricultural Biological & Environmental Statistics, 2000,5(2):131-150.

[15] STROZZI T, KOURAEV A, WIESMANN A, et al. Estimation of Arctic glacier motion with satellite L-band SAR data [J]. Remote Sensing of Environment. 2008,112(3):636-45.

[16] YOO J C, HAN T H. Fast Normalized Cross-Correlation[J]. Circuits Systems & Signal Processing, 2009,82(2):144-156.

[责任编辑：刘文霞]

An offset-tracking method based on least square adjustment of full polarimetric

SARMAO Xiaokang，WANG Changcheng，ZHOU Yushan，WANG Huiqiang

(School of Geosciences and Info-Physics Central South University,Changsha 410083,China)

Comparing with single-channel SAR image, the full polarimetric synthetic aperture radar image (PolSAR) has more abundant terrain information. To improve the offset estimation accuracy of SAR images, the paper proposes an offset-tracking method based on least square adjustment of full polarimetric SAR data. Firstly, the multiple offset observes are obtained of different polarimetric channel SAR images. Then the least square adjustment is used to eliminate the errors and get the optimal results. Finally, two JPL UAVSAR full polarimetric SAR images are selected to cover Lake City, Colorado, USA for validating the proposed method. The experimental results show that, compared with the single-channel SAR image, the offset errors of the proposed method decrease significantly. The precision of offsets in range and azimuth improves by 15%～25%. The proposed method improves the accuracy of offset tracking. It is significant to use the offset-tracking method for monitoring deformation of landslide, earthquake and glacier.

full polarimetric SAR; least squares adjustment; offset tracking; registration；error

10.19349/j.cnki.issn1006-7949.2017.03.005

2016-03-04

国家自然科学基金资助项目(41371335)

毛晓康(1990-)，男，硕士.

P237

A

1006-7949(2017)03-0023-05

引用著录：毛晓康，汪长城，周玉杉，等.基于最小二乘平差的全极化SAR配准偏移量估计方法[J].测绘工程，2017，26(3)：23-27.