基于震荡序列的灰色预测模型在边坡沉降监测中的应用

王 岩，黄张裕，张玉爽，艾合塔木·依米尼亚孜,王文利

(河海大学 地球科学与工程学院，江苏 南京 211100)



基于震荡序列的灰色预测模型在边坡沉降监测中的应用

王 岩，黄张裕，张玉爽，艾合塔木·依米尼亚孜,王文利

(河海大学 地球科学与工程学院，江苏 南京 211100)

公路边坡由于施工的影响，监测点时升时降，累计沉降量是震荡序列。本文采用三种模型对累计沉降量进行预测。结果表明GM(1,1)和DGM(1,1)预测曲线并不能反映实测值曲线走势，预测值与实测值的偏离程度较大，预测精度较低。SDGM(1,1)模型无论在与实测值曲线走势、与实测值接近程度还是在残差平方和或者平均相对误差上精度要高于其他两种模型，在P,C值上，SDGM(1,1)模型实现“级”的跳跃，是一个非常理想的预测模型。

边坡沉降；震荡序列；SDGM(1,1)预测模型

公路边坡失稳产生极大的安全隐患，严重威胁车辆和行人的安全。要保证通行安全，保护生命财产不受损失，对边坡进行变形监测并进行预报。自邓聚龙提出龙灰色理论以来，产生许多新的灰色预测模型，灰色预测模型由传统的GM(1,1)发展到GM(1,N)、GM(2,1)、DGM(1,1)、IDGM(1，1)、FGM(1,1)、GOM(1,1)、Verhulst等[1-5]。

根据GM(1,1)、DGM(1,1)模型的建模原理和大量实验表明，两模型对满足单调递增的数据列一般具有较高的预测精度，而对其他类型数据列，其预测精度是不确定的。许多灰色理论研究者对原始数据列进行变换，以提高其光滑性，取得了十分好的效果[6-8]。本文结合某边坡沉降监测实例，对沉降进行预报,在分析沉降监测数据时发现数据列是震荡序列，而GM(1,1)、DGM(1,1)模型对该类型数据列的预测精度较差[9-11]。压缩震荡序列的振幅，是序列变得平滑，改善数据列的平滑度可以提高沉降预测的精度，在此基础上产生了基于震荡序列的灰色预测模型，将该模型简称为SDGM(1,1)模型。SDGM(1,1)模型无论在与实测值曲线走势、与实测值接近程度还是在残差平方和或者平均相对误差上精度都要高于另外两种模型，在P，C值上，SDGM(1,1)模型实现了“级”的跳跃，是一个非常理想的预测模型。

1 GM(1,1)模型

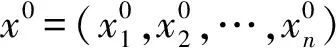
对数列x1建立微分方程

，

(1)

用最小二乘法求得[a,b]T=(BTB)-1BTYN。

对微分方程(1)求解，得出

(2)

累减生成后的还原数据为

(3)

，

其中

，

2 基于震荡序列的灰色预测模型

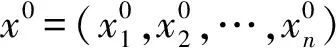
表1 模型精度等级

，

k=1,2,…,n-1.

(4)

进而可得平滑序列y0的DGM(1,1)模型还原式

(5)

将序列y0改为原始数据列，就原始数据列DGM(1,1)模型的建模过程，此处不再赘述。

由(4)可知

).

(6)

当k为奇数时，

，

(7)

将式(5)、式(7)联立可得还原式

，

(8)

同理，当k为偶数时还原式

，

(9)

3 实例分析

使用精密水准仪按二等精密水准观测方法对某公路边坡进行沉降监测，共布设28个沉降监测点，以7 d为一个观测周期，共观测11个周期。由于观测精度较高，本文简单地将实测值作为真值看待。本文选取任一监测点分析，发现该点累计沉降量序列是震荡序列。由于边坡十米外就是长江，随着铺设输油管道工程不断进展，再加上监测点附近不断有重型车进行施工，引起了地下水的上升和下降，引起边坡时升时降，其累计沉降量序列为震荡序列。运用JAVA对该点实现具体的算法，得到三种模型的模拟值(预测值)，其累计沉降量(实测值)、模拟值(预测值)如表2所示，其中预(G)、预(D)、预(S)分别表示GM(1,1)、DGM(1,1)、SDGM(1,1)模型的模拟值(最后两列为预测值)。表2中的实测值和预测值均为负值(表中数据的相反数)。

表2 实测值和预测值 mm

三种模型的P值、C值、平均相对误差、残差平方和如表3所示。

表3 三种模型的P值、C值、相对误差平均值、残差平方和

从表3可以看出SDGM(1,1) 模型的C值远小于0.35，模型精度等级处在一级(好)水平上，而GM(1,1)、DGM(1,1)模型的C值大于0.35，模型精度等级处在二级(合格)水平上，可见使用SDGM(1,1) 模型较另外两种模型精度实现了“级”的跳跃，大大提高预测质量。

无论是SDGM(1,1) 模型预测值的残差平方和还是平均相对误差和另外两种模型相比都不在同一个量级上，残差平方和是另外两种模型的十分之一，平均相对误差是另外两种模型的五分之一，这都说明了SDGM(1,1)模型的预测精度要高于另外两种模型，说明对于震荡序列的预测SDGM(1,1)是理想的预测模型。

为了更形象的表现出三种模型的预测值与实测值的偏离程度，将三种模型的预测曲线和实测值曲线绘制成图，如图1所示。

图1 模型预测曲线和实测值曲线

从图1发现，只有SDGM(1,1)预测曲线与实测值曲线的走势相符，预测值与实测值偏差较小，与实测值曲线较为相近，是对震荡序列进行预测的理想模型。GM(1,1)和DGM(1,1)测曲线走势并不符合实测值曲线，从第三周期以后只是单纯的单调递增，这说明了GM(1,1)和DGM(1,1)模型只适合对单调递增数据列进行预测，不适合对震荡序列进行预测。

4 结束语

由于施工的影响，监测点时升时降，累计沉降量数据列是震荡序列。本文采用三种模型对边坡沉降进行预测，对比3种模型的精度，发现SDGM(1,1)模型无论在与实测值曲线走势、与实测值接近程度还是在残差平方和或者平均相对误差上精度要高于另外两种模型，在P，C值上，SDGM(1,1)模型实现了“级”的跳跃，是一个非常理想的预测模型。

[1] 郭君,甘德清,张伟航,等. GM(1,N)模型在边坡变形监测中的应用研究[J]. 现代矿业,2010(8):41-43.

[2] 王冬,黄鑫,王明东,等. 灰色GM(2,1)模型在滑坡变形预测中的应用[J]. 水文地质工程地质,2013(3):121-125.

[3] 李仙虎,田川,易富君. 非等时距DGM(1,1)模型及其在路基沉降预测中的应用[J]. 交通运输工程与信息学报,2012(4):31-35.

[4] 宋中民,邓聚龙. 反向累加生成及灰色GOM(1,1)模型[J]. 系统工程,2001(1):66-69.

[6] 钱和平,周根宝. 基于对数变换的灰色GM(1,1)改进模型[J]. 内蒙古农业大学学报(自然科学版),2009(2):257-259.

[7] 张军,王秋萍,周杰,等. 一种提高灰色模型拟合精度的简便方法[J]. 西南民族大学学报(自然科学版),2007(5):1070-1074.

[8] 钱吴永. 数据变换技术与GM(1，1)模型研究[D].南京：南京航空航天大学,2009.

[9] 杨芬,关叶青,曾波,等. 基于随机振荡序列的DGM(1,1)模型的建模及应用[J]. 数学的实践与认识,2013(16):175-180.

[10] 邹俊华，刘荣. 变形监测双重加权DPGM(1,1)预测模型的建立[J].测绘与空间地理信息，2016，39(2)：47-49. [11] 曾波. 灰色预测建模技术研究[D].南京：南京航空航天大学,2012.

[责任编辑：李铭娜]

Application of grey prediction model to slope settlement monitoring based on shock sequence

WANG Yan,HUANG Zhangyu,ZHANG Yushuang,AIHETAMU·Yiminiyazi,WANG Wenli

(School of Earth Science and Engineering， Hohai University，Nanjing 211100，China)

The construction of highway slope raises and lowers the monitoring points,of which the cumulative amount of the settlement is the shock sequence. In this paper, three models are given to predict the cumulative settlement.The results show that GM (1,1) and DGM (1,1) prediction curve can not reflect the actual value of the curve trend, large deviation between the predicted and measured values of the low prediction accuracy.SDGM (1, 1) model in proximity or curve moves, with the actually measured value and the measured values on the residual peace or average relative error of accuracy compared with other two kinds of model,has a higher accuracy.In value P and C, this model also can achieve a “level” jump,which is a very ideal prediction model .

slope sedimentation; shock sequence; SDGM (1, 1) prediction model

10.19349/j.cnki.issn1006-7949.2017.03.015

2016-05-31

王 岩(1990-)，男，硕士研究生.

TV196

A

1006-7949(2017)03-0069-03

引用著录：王岩，黄张裕，张玉爽，等.基于震荡序列的灰色预测模型在边坡沉降监测中的应用[J].测绘工程，2017，26(3)：69-71，76.