隧道三维点云孔洞修复方法

钱伯至，蓝秋萍

(河海大学 地球科学与工程学院，江苏 南京 211100)



隧道三维点云孔洞修复方法

钱伯至，蓝秋萍

(河海大学 地球科学与工程学院，江苏 南京 211100)

针对隧道三维激光扫描点云中的孔洞，设计一种基于断面轮廓的孔洞修复方法。隧道具有深长性与截面恒定性两大特征，文中基于这两大特征，利用间邻稳定轮廓拟合完整隧道修复孔洞。该方法能够对三维激光扫描点云进行圆柱投影，利用Delaunay三角构网，提出基于隧道表面三角网的孔洞识别方法，最后根据相邻隧道轮廓相似的特点，利用相邻的轮廓对孔洞进行修复。该方法能很好的修复孔洞并保留隧道结构细节，并以真实的隧道扫描数据验证算法的有效性和可靠性。

三维点云；Delaunay 三角构网；孔洞识别；孔洞修补

近年来，随着交通建设发展，隧道得到人们关注，而隧道的变形监测是隧道建设中必不可少的一项环节。由于隧道存在光线不足、狭长等问题，常规的测量难以适用于隧道，而三维激光扫描技术又称为“实景复制技术”，它具有非接触、扫描速度快、获取信息量大、精度高且对环境要求较低等优点[1]。激光扫描通过自主发射光束，可以解决隧道光线不足的问题，适合隧道参数的测量。

然而因为隧道内交通不可中断，且扫描仪的扫描垂直角存在一定的限度，致使隧道扫描点云中存在大量孔洞。从现有的文献可见，目前已有许多孔洞修复的方法：如多视图立体三维重建孔洞修复算法[2]，该方法基于视图重建得到的三维点云与可见外壳点云融合算法[3-4]，在点云的稀疏度约束和曲率约束下修复点云，然而该方法对部分凹型区域也进行一定修复，对原有结构造成一定破坏；晏海平等提出基于径向基函数的散乱点云孔洞修复算法[5]，通过内外边界边的识别进行孔洞识别，然后基于径向函数的隐式曲面插值修复孔洞[6-7]，但是对于边缘这类突变棱角，利用连续光滑曲面的约束条件重建缺失数据显然有违于原始对象的几何特征。

本文基于隧道轮廓的特征，利用相邻隧道断面轮廓修复孔洞。基于隧道断面轮廓线检测的孔洞识别最优截面模型，以中轴线为基础复刻完整隧道，实现孔洞拟合修复。

1 截取断面轮廓

1.1 中轴线计算及三角构网

图1 角度与轴线距离匹配

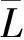
表1平均边长变化规律表

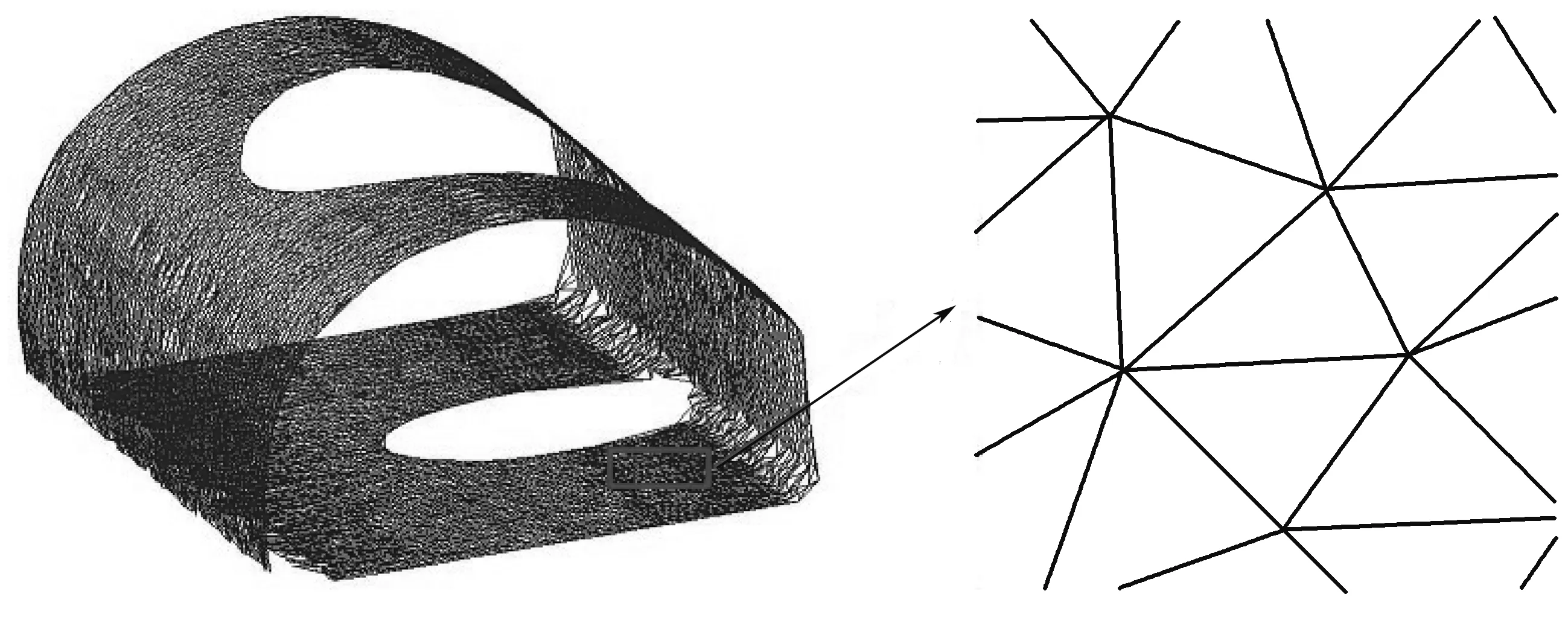
图2 三角网网型

1.2 断面轮廓截取及孔洞识别

基于隧道表面三角网，采用垂直于中轴线的截断面与三角网进行空间求交获得交点。Delaunay三角构网后所形成的隧道三角网网型较密且孔洞范围内也存在三角网，在截取断面轮廓线时难以区别孔洞。根据隧道孔洞附近三角网特点打断孔洞位置的三角网边，显现孔洞。

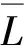
图3 点云孔洞

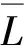
图4 断面截取

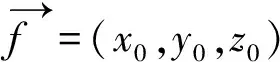
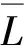
2 轮廓线修复

从隧道的特征出发，利用相邻完整的断面轮廓对孔洞位置进行修复。隧道内壁上存在吊灯、通风扇、管线等附属物，使得隧道断面轮廓有细微的差别，本文采用识别最优轮廓的方式，甄别出与需要填补的断面轮廓最相似的断面，并以此断面为基准进行平移修补。最后利用补充中点的方式对隧道检修道进行孔洞修复。

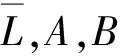
(1)

图6中黑色点表示待修复断面P，红色点为某

图5 孔洞修复

图6 最优轮廓面

由于三维激光扫描的特点，导致隧道内检修道面等曲率变化很小的结构在每个截断面上的点都比较少，经过上述方法修复孔洞后该结构依旧会存在小孔洞，在已经保留隧道结构细节的前提下，对该结构利用插入中点的方式修复孔洞，使得隧道所有孔洞均被修复，且保证隧道内部的结构细节不被破坏。

3 实验分析

实验数据来自宁杭高速梯子山隧道的三维激光扫描点云，本次实验采用该隧道其中某一测站的点云数据，点云个数为187 568个，该段隧道长度为108.785 m。隧道三维激光扫描过程中交通不可阻断，所以隧道竖直墙面存在由汽车等物体遮挡所导致的孔洞，且由于扫描仪本身扫描垂直角存在一定限度，使得测站中心所在位置的拱顶与地面存在较大孔洞。实验利用上述方法对隧道孔洞进行修复，并保留吊灯、通风扇、管线等附属物。

对点云进行三角构网并截取断面轮廓。依据断面轮廓线的长度可识别孔洞的存在。随后利用相邻断面轮廓进行孔洞修复(根据修复效果，可进行多次修复，以保证孔洞修复点云均匀)。最后通过插入中点的方式进行修复，完成孔洞的修复。

图7(a)为隧道原始点云，(b)表示隧道拱顶存在的吊灯，(c)表示隧道拱顶和路面的孔洞，(d)表示隧道竖直墙面由于遮挡物遮挡导致的小孔洞。进行轮廓线修复后，效果见图8。

图7 隧道点云孔洞

图8 修复后的点云

图8是修复后隧道三维激光扫描点云，其中红色为原始点云，绿色为修复后的点云，(a)中可以看出道路和拱顶的两个孔洞被修复，(b)表示隧道两侧的小孔洞已被修复，(c)表示隧道吊灯在修复孔洞时被保留，(d)为修复过后隧道三维激光扫描点云沿中轴线方向观察的形状结构，图中可以看出修复后隧道结构细节依旧保持完整。

4 结束语

针对隧道三维激光扫描点云孔洞提出一种可行的修复算法。基于点云平面拟合所得的法向量，实现高精度中轴线的获取，同时讨论“在利用圆柱投影构建隧道三角网过程中，投影后两个坐标尺度差异对三维构网结果的影响”，并给出统一坐标尺度的方法，通过计算一个合适的半径，将圆柱投影所得的弧度值转换成弧度所对应的弧长，确保坐标尺度一致。利用Delaunay平面构网方式对点云进行三角构网，最后利用残缺断面的非残缺点到参考断面轮廓线的距离，优选出用于修复的参考断面，并利用该断面的截断点修复孔洞，再加入插值孔洞修复法，以保证所有孔洞都已被修复。实验结果表明，本文的算法不仅能完美地修复隧道点云的孔洞，且能确保隧道细节不被破坏。然而该方法目前只适用于直线型隧道，对于弯曲型隧道，由于中轴线随隧道方向的变化而改变[15]，从而导致截断面之间点的互相填补不能靠简单的直线平移进行修复，有待进一步的研究。

[1] 崔磊，张凤录.面三维激光扫描系统内外业一体化研究[J].北京测绘，2013(1):47-49.

[2] 吴晓军，文飞，温佩芝.视图立体三维重建中的孔洞修复[J].计算机辅助设计与图形学报，2012，24(12)：1606-1613.

[3] SONG P, WU X J, WANG Y. A robust and accurate method for visual hull computation[C]//Proceedings of IEEE International conference on Information and Automation. Los Alamitos: IEEE Computer Society Press,2009:784-789.

[4] SONG P, WU X J, WANG M Y .Volumetric stereo and silhouette fusion for image-based modeling[J].The Visual Computer,2010,26(12):1435-1450.

[5] 晏海平，吴禄慎，陈华伟.基于径向基函数的散乱点云孔洞修复算法[J].计算机工程与设计，2014，35(4)：1253-1257.

[6] 刘越华，廖文和，刘浩.逆向工程中散乱点云的K邻域搜索算法研究[J].机械设计与制造，2012(2):256-258.

[7] 孙殿柱，朱昌志，李延瑞.散乱点云边界特征快速提取算法[J].山东大学学报(工学版)，2009，39(1)：84-86.

[8] 蓝秋萍，洪超，林欢，等.三维点云中自动提取隧道特征线[J].测绘工程，2015，24(10)：1-4.

[9] 曹诗卉，亓迎川.基于最小二乘法平面拟合的点云法矢算法[J].计算机技术，2016，30(1)：41-43.

[10] GREEN P J.SIBSON R.Computing Dirichlet tessellations in the plane[J].Computer Journal,1978,21(2):168-173.

[11] BRASSEL K E,REIF D.A procedure to generate Thiessen polygons[J].Geographical Analysis,1979,11(3):289-303.

[12] MCCAULLAGH M T,ROSSC G.Delaunay triangulation of a random data set isarithmic mapping[J].The Cartographic Journal,1980,17(2):93-99.

[13] MAUS A.Delaunay triangulation and the convex hull of n points in expected linear time[J].Bit Numberical Mathematics,1984,24(24):151-163.

[14] 余杰，吕品，郑昌文.Delaunay三角网构建方法比较研究[J].中国图像图形学报，2010,15(8)：1158-1167.

[15] 汪子豪. 从隧道三维点云中自动截取断面轮廓的方法[J].水利与建筑工程学报，2015(2)：47-52.

[责任编辑：张德福]

Repairing tunnel 3D point cloud hole

QIAN Bozhi, LAN Qiuping

(School of Earth Science and Engineering, Hohai University,Nanjing 211100，China)

Due to the hole in tunnel 3D laser scanning point cloud, this paper designs a hole-filling method based on cross-sections. Tunnel is narrow and the cross-sections are similar, so the nearby intact cross-sections can be used to repair the hole. First of all, this paper changes 3D laser scanning point cloud into 2D by cylindrical projections and then comes up with a method to recognize the hole after constructing the Delaunay triangles. Finally, because the nearby cross-sections are similar, the hole is repaired with the nearby cross-sections. This method can not only repair the hole effectively, but also keep tunnel detail structure without destroyed. The effectiveness and reliability of this method are verified with the scanning data form a real tunnel.

3D point cloud; Delaunay triangle construction; hole identification; hole repair

10.19349/j.cnki.issn1006-7949.2017.03.010

2016-05-18

国家自然科学基金资助项目(41301406)；江苏省自然科学基金资助项目(BK20130829)

钱伯至(1994-)，男，本科生.

P231

A

1006-7949(2017)03-0046-05

引用著录：钱伯至，蓝秋萍.隧道三维点云孔洞修复方法[J].测绘工程，2017，26(3)：46-50，55.