基于距离贪心策略的灰狼特征选择算法研究*
童坤 钮焱 李军
(湖北工业大学计算机学院 武汉 430068)
1 引言
现今科技高速发达的今天,医疗检测系统不断更新换代,检测体系日趋成熟。心脏病作为人类健康的杀手,在疾病发作之前对其进行检测具有重大的意义。而病人生理数据特征量大且冗杂,冗杂的特征使得心脏病检测的工作量变得巨大,且效果还会变得不佳。灰狼优化算法(Grey wolf optimization,GWO)是现在被投入使用的群体智能算法,该算法通过模拟狼群捕食猎物的过程,来确定所要捕食的猎物的位置,也就是优化问题的最优解,并且被大量用于特征选择部分中[2~9],但是本身算法收敛速度较慢,搜索效率较低。本文提出了一个改进的灰狼算法用于特征选择部分,该算法用贪心策略代替了一般灰狼算法位置更新部分,提高了最优价的搜索效率,从而能抽取出较好的特征集,有利于样本的检测。
2 基于距离贪心策略的GWO
本文基于贪心策略,提出了一个GWO的新的二元编码化方法。该策略以个体离迭代最优点的距离为参照,其中离最优点最近的个体点最不容易改变编码,而距离最远的点则有最大的概率改变自己的编码。
2.1 距离贪心策略
该策略是基于灰狼个体和猎物之间的距离大小来实现的。一般来讲,贪心策略是在求解问题是,总是做出在当前看来是最好的选择,在灰狼算法的更新问题上,贪心策略可以设置为:在某一维距离最优点越近,其改变编码的概率越小,而距离最优点越远,则改变的概率越大。由图1可知,中心点为最优点prey,则有:
1)对于A狼和C狼来说,②的长度远小于③,则根据贪心策略,A狼在x轴上改变编码的概率远小于C狼。
2)对于A狼和C狼来说,④的长度远小于①,则根据贪心策略,C狼在y轴上改变编码的概率远小于A狼。
3)对于B狼来说,⑤和⑥的长度都比较大,故B狼无论x轴还是y轴,其改变的概率都较大。
故由以上贪心策略分析可知,编码在某一维改变的概率和该点某一维距离最优点的长度成正比,算法的中心则变成了如何计算出改变的概率。
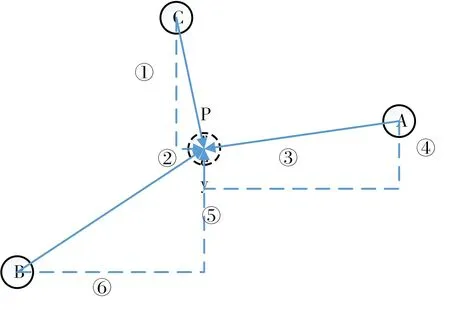
图1 贪心策略图示
2.2 基于距离贪心策略的GWO
该算法步骤分为三部分:计算连续编码距离向量,距离映射和更新离散编码距离向量。
1)计算连续编码距离向量
为了得出该个体二元编码向量的概率,必须先求出该个体距离最优点的连续位置距离,而在GWO中,最优点的位置由α,β和δ的位置所假设表示,当个体的位置离α,β和δ越近,则表明该个体所携带的解越优。故可以用离α,β和δ的距离来得出该个体距离最优点的连续位置距离。连续编码距离向量由式(1)计算出:和表示该个体距离α,β和δ的距离,其定义如下:和可有式(5)~(7)算出:和表示在第t次迭代中前三个最优的候选解。

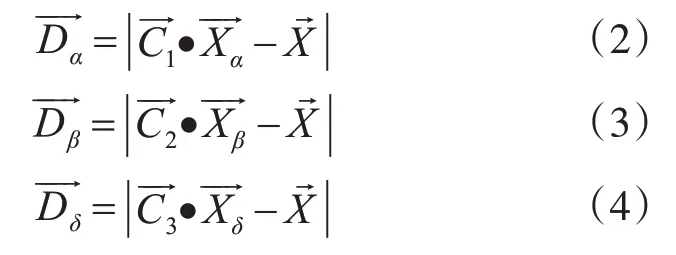
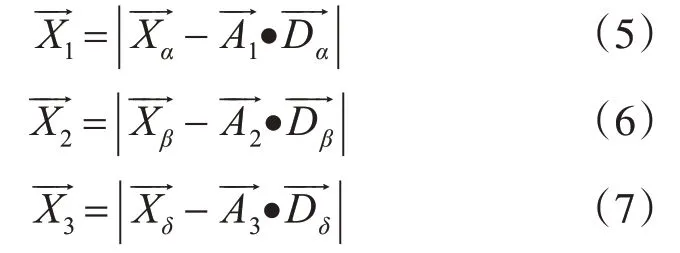


其中t为当次迭代的次数,maxiter为算法迭代的总次数。
2)距离映射
特征选择问题中的连续型变量的搜索区间是任意设置的,通常情况下,特征选择问题的搜索区间可以被人为设置为[0,1]。当问题搜索区间设置不为[0,1]时候,则需要通过一个映射函数将该问题转换为在区间[0,1]上的问题。假设问题搜索区间为[a,b],一个最简单的映射函数G()构造如下:
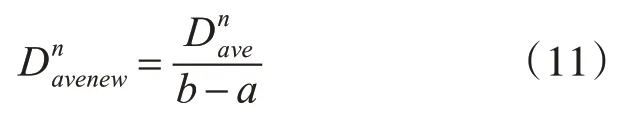
其中Dnave表示由式(1)所算出的第n维度的值,Dnavenew表示向量第n维度的值。
3)更新离散编码距离向量
更新编码向量的原则为以个体离迭代最优点的距离为参照,离最优点最近的个体点最不容易改变编码,而距离最远的点则有最大的概率改变自己的编码,当我们获得了取值范围在[0,1]的连续编码向量或)时,将和该个体二元编码向量作为更新策略f的输入,得到下一次迭代t+1中该个体的二元编码向量。设中的第d维取值为和连续编码向量的第d维取值为Dd,则对于每一维d,其更新策略如式(12):

其中rand为[0,1]区间里任意的随机数,其中hold和change表示对的操作,操作后的取值作为xd的值。change和hold的两个操作表示为如式(13)、(14):

更新策略根据Dd的取值来采取相应的操作,按照所选的操作来更新xd的取值,算法1表示该算法的执行步骤:
算法1 基于贪心策略灰狼优化算法
输入:种群中灰狼个体的数目n
算法迭代的总次数max_itr
初始化a,A和C三个控制参数。
随机初始化n头灰狼的位置向量
通过计算每个灰狼的适应值来找出α,β和δ的位置向量。
t=1
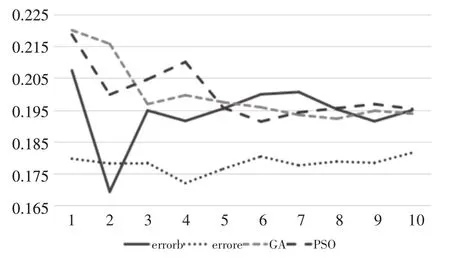
While(t For狼群中的每一头狼i For狼的位置向量的每一维 根据式(12)更新狼i第d维的取值 End End Ⅰ更新a,A和C三个控制参数 Ⅱ计算更新后每一头灰狼的适应值 Ⅲ更新α,β和δ End 本文使用uci数据库中的一组心脏病数据做为实验数据集,将优化过后算法和GWO,遗传算法(GA),粒子群算法(PSO)作为特征选择部分的算法,使用KNN作为样本分类器,将样本分类错误率和最终特征选择数目作为比较指标,比较使用这四种不同特征选择算法在不同的运行次数下的平均性能指标。。 本文实验所使用的数据集为UCI数据库所提供的一组心脏病数据集,一共303条数据,每条数据记录了心脏病人的所有生理指标。该数据特征表如表1。 KNN算法是一种简单的监督学习分类算法,它通过度量该样本在空间中的K个最相似的邻居(特征空间中最邻近的样本)大多数是属于哪一类,则该样本就属于这一类,所有的邻居都为已正确分类的对象。由于KNN分类器无需建立任何模型,只需要通过有限的邻居来确定所属类别,所以KNN被普遍用于各大分类问题中,KNN算法具有特别的优势[10~15]。 表1 心脏病数据特征表 算法参数设置如表2所示。 表2 BGWO和EBGWO算法参数设置 实验比较了四种不同特征选择算法在不同算法运行次数下的性能指标,算法运行次数从20次开始不断增加,一直到200次。图1和图2的横坐标表示的是算法运行次数,1表示第一次实验运行次数为20次,10表示第十次实验运行次数为200次。Errorb和countb表示使用原始灰狼算法做特征选择部分后的错误率和特征选择数,而Errore和counte表示使用改进后的灰狼算法做特征选择部分后的错误率和特征选择数。由图1可知,除了第2次实验之外(40次运行次数)之外,改进后的算法的分类准确度都优于其余所有的算法,平均错误率均在1.85%以下,效果有明显的提升,且波动幅度较小,运行效果较为稳定。由图2可知,在十次实验中,使用改进后算法的平均特征选择数都小于3.85,均低于PSO和GA的特征选择数目。而与改进前的灰狼算法相比,特征选择数减少了许多,且波动性也较为稳定。 图2 四种不同算法进行特征选择的检测错误率对比 图3 四种不同算法进行特征选择后的特征选择数目对比 本文提出了一种新的灰狼算法的二元编码化版本:基于距离贪心策略的二元灰狼算法。通过实验表明,在相同条件下,该算法在特征选择方面能够取得较好的效果。纵向对比,该算法特征选择后的检测错误率优于原始的BGWO,在特征选择数目方面优于改进版的EBGWO,总体来讲集合了两种算法的优点。横向对比,该算法无论从特征选择数还是检测错误率,都优于PSO和GA,而且该算法收敛速度较快,能在较少的迭代次数下达到较好的效果。3 实验及其结果分析
3.1 数据集及分类器准备

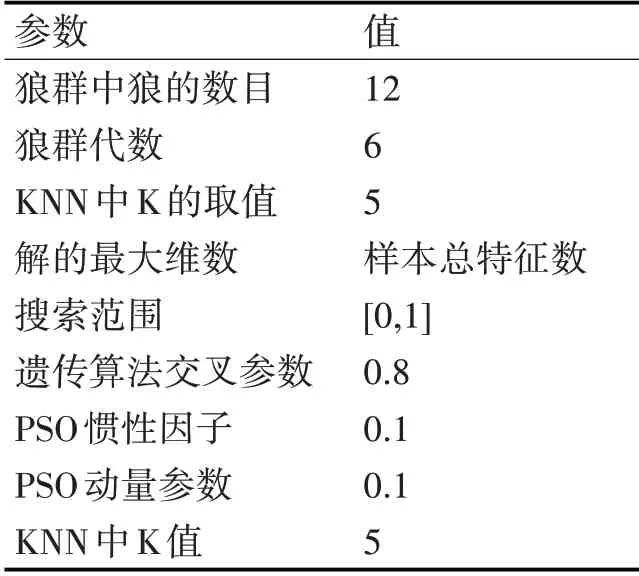
3.2 算法参数设置
3.3 实验结果

4 结语

