考虑驾驶风格的模糊控制跟驰模型
吴 兵,罗 雪,李林波
(同济大学道路与交通工程教育部重点实验室,上海201804)
车辆跟驰模型是微观交通流的一个基本模型[1],传统跟驰模型中,后车的驾驶决策与前车的刺激存在着一一对应的关系。在实际行驶过程中,驾驶人对其他车辆的行驶状态所作出的反应,不一定是线性关系,更多的是根据驾驶经验和驾驶情况所决定的,因此引入模糊控制跟驰模型,来模拟驾驶人对于车辆决策的过程。
最早把模糊控制方法引入跟驰模型的学者是Kikuchi 和Chakroborty[2],在实际道路条件下,对一辆跟驰车辆采集其车头时距和速度数据,对人的感知和推理过程中固有的不精确性进行了研究,建立模糊控制规则并进行仿真模拟,结果表明,与传统GM(general motors)模型相比,该模型具有局部稳定性,在一定程度上能够预测驾驶人或车辆反应的变化。在此基础上,Khodayari 等[3]将模糊控制的输入参数增加为瞬时反应延迟、相对速度、相对距离和后车速度,通过NGSIM(next generation simulation)数据进行了模型验证,证明其对驾驶人行为预测方面效率较高。Mar和Lin[4]对跟驰模型的模糊控制系统进行了持续的研究,首先提出了一种基于自适应网络模糊控制系统的汽车追尾防碰控制器,解决前车与后车距离和相对速度的振荡问题,随后提出了一种基于模糊函数网络的汽车跟驰防碰控制器,实现汽车速度的非线性控制[5],然后提出了一种基于级联模糊控制系统的车辆跟驰、变道防碰系统设计方案[6]。Xiong[7]对模糊控制模型的隶属度函数进行研究,采用最小二乘法对离散数据进行拟合,得出隶属度函数。王文清等[8]提出了考虑最小安全距离的跟驰模型,用模糊控制来模拟驾驶人控制车辆的行为。邱小平等[9]建立相应的车辆跟驰模糊控制系统,采用NGSIM 数据进行模型标定,并与Gipps 模型进行对比评价,发现模型拟合更优。
目前大部分基于模糊控制的跟驰模型,假设驾驶人的驾驶行为方式相同,然而,在真实的交通流中,驾驶人的年龄、身体素质、反应敏感性、驾驶技能等个体差异导致了不同的跟驰行为[10-12],同时驾驶人心理生理活动是不确定的、复杂的[13],同一数学模型无法准确描述所有驾驶人的跟驰行为。因此,有学者开始对不同类型的驾驶人的特点进行研究,将驾驶人分为激进型、温和型和保守型三种,但在隶属函数划分部分和模型验证时,由于缺乏真实数据支撑,仅进行了定性分析[14]。
实际上,同一个驾驶人在不同状态下也会呈现出不同的驾驶风格,基于此,本研究拟针对不同驾驶风格,利用自然驾驶跟驰数据,定量分析不同驾驶风格对模糊变量的影响,并提出相应的模糊控制跟驰模型,深入探讨驾驶风格对模糊控制模型的影响。
1 数据来源及处理
1.1 基本数据
本研究的数据来自“上海自然驾驶研究”项目的中国驾驶人自然驾驶数据,数据情况见表1。

表1 中国驾驶人自然驾驶数据情况Tab.1 Naturalistic driving data of Chinese drivers
1.2 跟驰片段提取
在跟驰片段分析之前,需要确定车辆跟驰过程中一些关键变量的阈值范围,因此,参考已有研究[15],对侧向距离绝对值、自车速度、纵向距离、相对速度绝对值、跟驰持续时间的约束见表2,保证车辆处于跟驰状态中。

表2 跟驰片段提取准则Tab.2 Extraction criteria of car-following segment
利用表2 的提取准则,通过编程对跟驰片段进行提取,共提取2 350 个自然驾驶快速路跟驰片段,跟驰片段平均持续时间为18.62 s,跟驰车辆的平均车速49.93 km·h-1(13.87 m·s-1),累计时长为729 min。
1.3 跟驰片段分析
分析提取的快速路跟驰片段数据,车头时距分布在0.41~5.95 s之间,平均车头时距为1.66 s。每个跟驰片段的跟驰车辆平均车速与平均车头时距散点图如图1所示,车头时距的直方图如图2所示。
由图1可知,随着车速增加,车头时距变化不显著,不同车速下车头时距的分布较相似,车速和车头时距没有明显关系,同一车速对应不同车头时距,反之亦然,无规律可循,与文献[16-18]结论相似。值得注意的是,车速为20~80 km·h-1的车头时距中3 s以上的比较少。从分布图2 的变化趋势观察,车头时距在1.3 s 左右出现概率的峰值,且集中于1~2 s范围内,随着车头时距的增加,相应比例降低。因此,车头时距的分布未以峰值为中心左右对称,而是在分布右侧出现“长尾”现象,呈正偏态分布,这一分布规律与文献[19-20]结论类似。
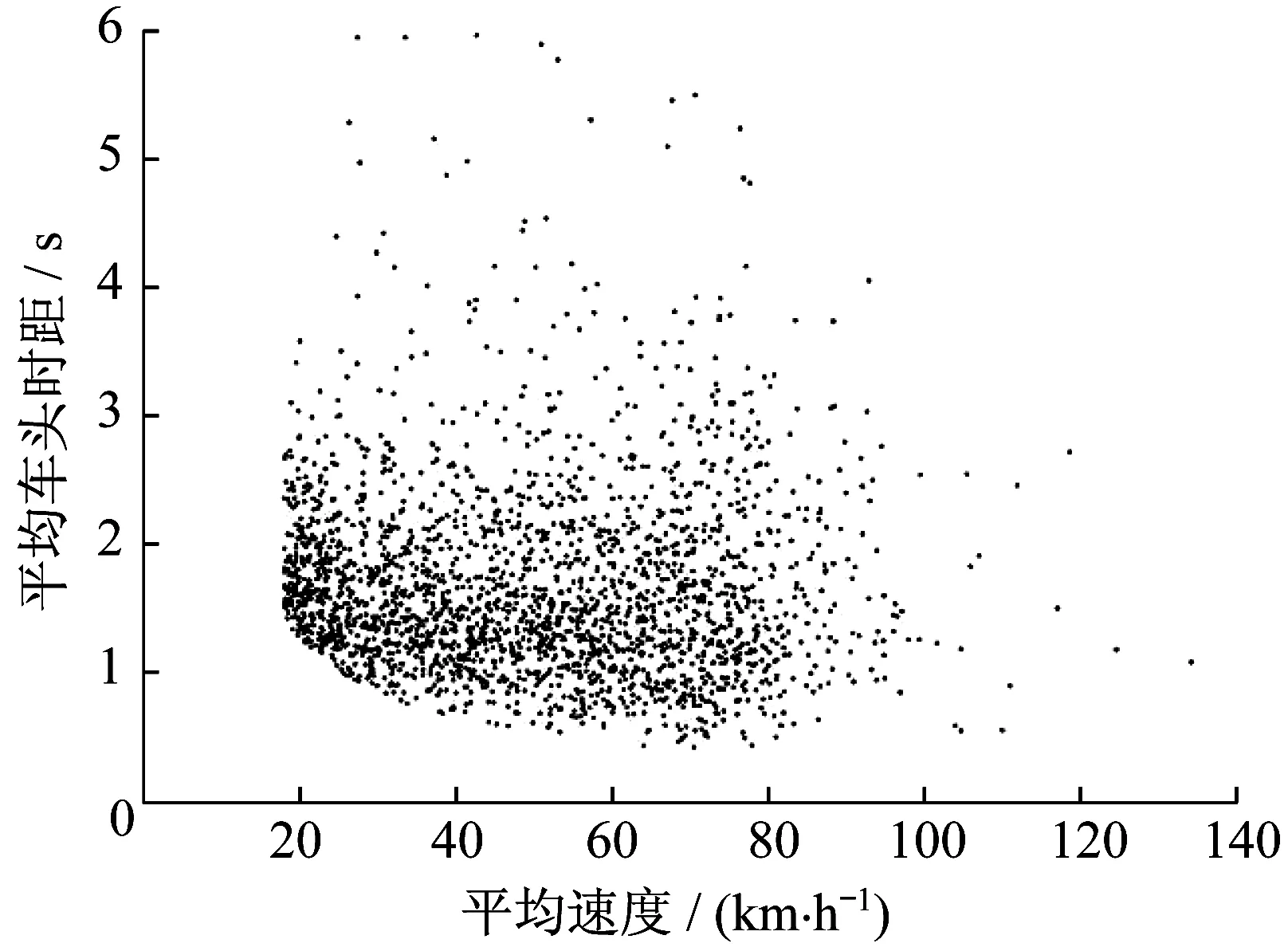
图1 车速与车头时距的散点图Fig.1 Scatter diagram of speed and time headway
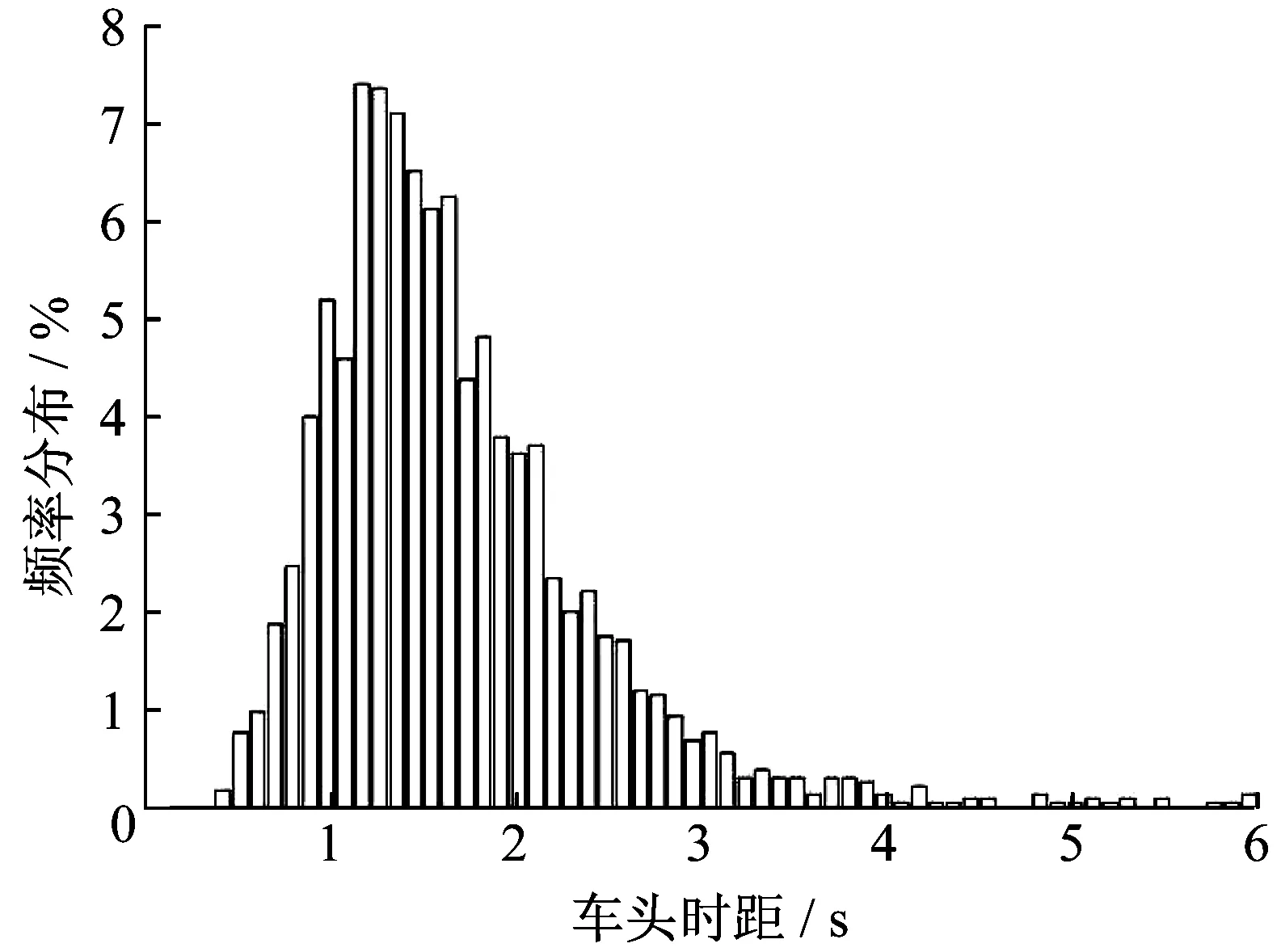
图2 跟驰片段车头时距的频率分布图Fig.2 Frequency distribution of time headway in car-following segment
为分析跟驰车头时距与驾驶人个体特性的相关性,对56 名驾驶人的跟驰片段进行归类分析,并按照车头时距大小排序,结果如图3 所示。图中每一个小图为同一驾驶人的所有跟驰片段车头时距分布(按照从小到大排序),横坐标为按照平均车头时距大小排列后的跟驰片段序列数,纵坐标为驾驶人的每个跟驰片段平均车头时距长度。
由图3可发现,同一驾驶人在不同的状态下,跟驰片段车头时距分布呈现波动性,并且同一驾驶人的跟驰片段数量越多,波动性越明显,表现出驾驶人在不同状态下,心理生理活动的不确定性和复杂性,参考已有的驾驶人分类[10,12,21-22],将驾驶类型分为三种类型:激进型、普通型和保守型。因此,实际的车头时距数据可以由三类满足不同分布的数据组成。假设三类驾驶风格车头时距满足正态分布[19-20],激进型的概率密度函数为f (x)ATH,普通型的概率密度函数为f (x)NTH,保守型的概率密度函数为f (x)CTH。则实测车头时距数据应满足理论分布:
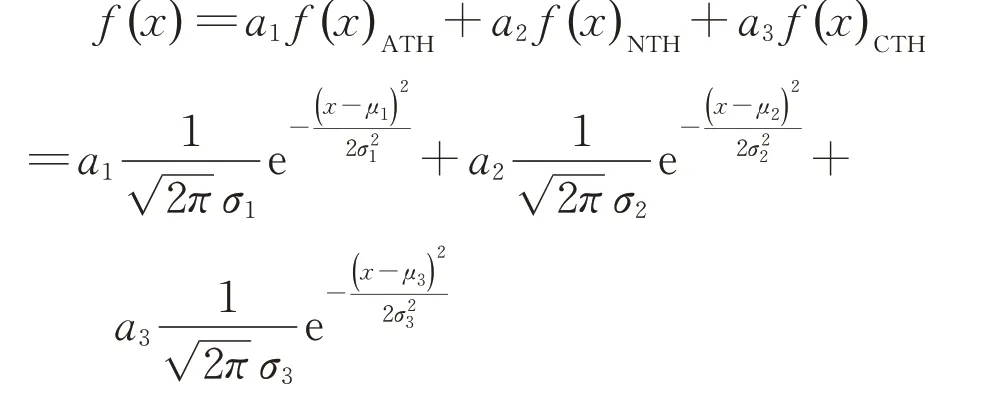
式中:a1、a2、a3为不同类型驾驶风格比例,满足a1+a2+a3=1;μ1、μ2、μ3为正态分布函数的位置参数;σ1、σ2、σ3为正态分布函数的变异度参数。
利用MATLAB 中fittype 函数进行混合正态分布函数拟合,得到三类驾驶风格的期望车头时距分别为:μ1=1.15,μ2=1.95,μ3=3.39,根据期望车头时距得出对应的车头时距区间见表3。

表3 期望车头时距Tab.3 Desired time headway

图3 驾驶人跟驰片段车头时距分布Fig.3 Driver based time headway distribution of car-following segment
2 模型建立
设有论域U,其中的任意个体u∈U,那么在该论域上的一个模糊集合A~ 定义为一组有序对A~ ={(μA~(u),u)|u∈U}。其中,μA~(u)或μA~ϵ[0,1]是模糊集合A~ 的隶属函数,它把论域U 中的每个元素映射到0 和1 之间,越接近1 表征u 属于μA~ 的程度越高[23]。
设计模糊控制原理4 个计算步骤:①确定期望距离差和速度差;②把期望距离差和距离差的确切值变成模糊状态作为输入量;③由模糊控制规则(即合算法)计算出模糊控制量aF;④将由③算出的模糊控制转化为确切的值加载到对象上。
2.1 模型变量
基于模糊推理跟驰模型的相关研究[2,4-7,22],本研究的输入变量:
(1)后车与前车的实际距离ΔlR与期望距离ΔlD之差Δl:
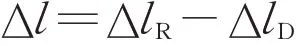
式中:期望距离ΔlD为期望车头时距tHW和后车速度vF之积[24]。
(2)前车速度vL与后车速度vF之差Δv:

输出变量:后车加速度aF:
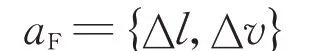
2.2 变量论域
根据模糊控制参数论域的确定方法,在提取的跟驰片段中,对前车与后车的车头间距进行计算,每个跟驰片段提取最大车头间距、最小车头间距、平均车头间距,如图4 所示,并分别与期望距离求差值,如图5所示。后车与前车的实际距离ΔlR与期望距离ΔlD之差Δl ∈(-40,40),单位:m,若分为11 级,期望距离差论域X:
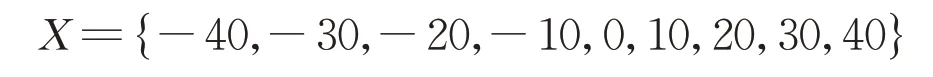
取7 个语言值,A~i(i=1,2,…,7)是论域X 上的模糊集,分别代表正大(PB)、正中(PM)、正小(PS)、零(Z)、负小(NS)、负中(NS)和负大(NB),隶属函数采用三角形函数分布。
同理,前车速度与后车速度之差如图6 所示,Δv ∈(-5,5),单位:m·s-1,速度差论域Y:

取7个语言值,B~j(j=1,2,…,7),隶属函数采用三角形函数分布。

图4 前车与后车实际距离Fig.4 Actual distance between the front vehicle and the rear vehicle

图5 实际距离与期望距离之差Fig.5 Difference between the actual distance and the expected distance
后车加速度如 图7 所示:aF∈(-9,3),单位:m·s-1,其论域为Z:
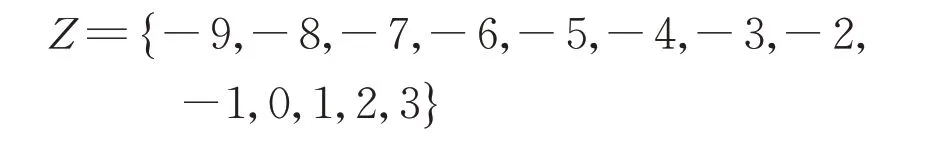
取7 个语言值,C~k(k=1,2,…,7),隶属函数采用三角形函数分布。
2.3 模糊控制的跟驰模型建立
模糊控制规则用下列符合条件语句表示:
每一条语句对应一个模糊关系,即:
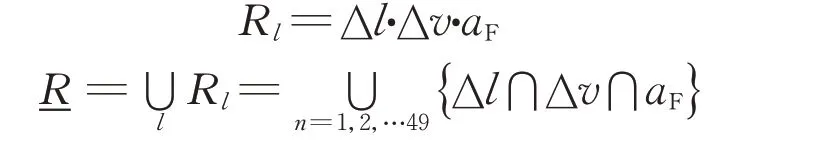
根据数据规律,确定49 条模糊控制规则,如表4所示。

表4 模糊控制规则表Tab.3 Fuzzy control rules
根据模糊控制原理建立考虑驾驶风格的模糊控制跟驰模型框架[25],如图8所示,其中将不同的驾驶风格转化为车头时距,通过输入该参数变量来反映三种驾驶风格的差异。本模糊控制系统采用面积中心法作为清晰化规则,求出模糊集合函数曲线和横坐标包围区域面积的中心,选择这个中心对应的横坐标值,作为这个模糊集合的代表值。
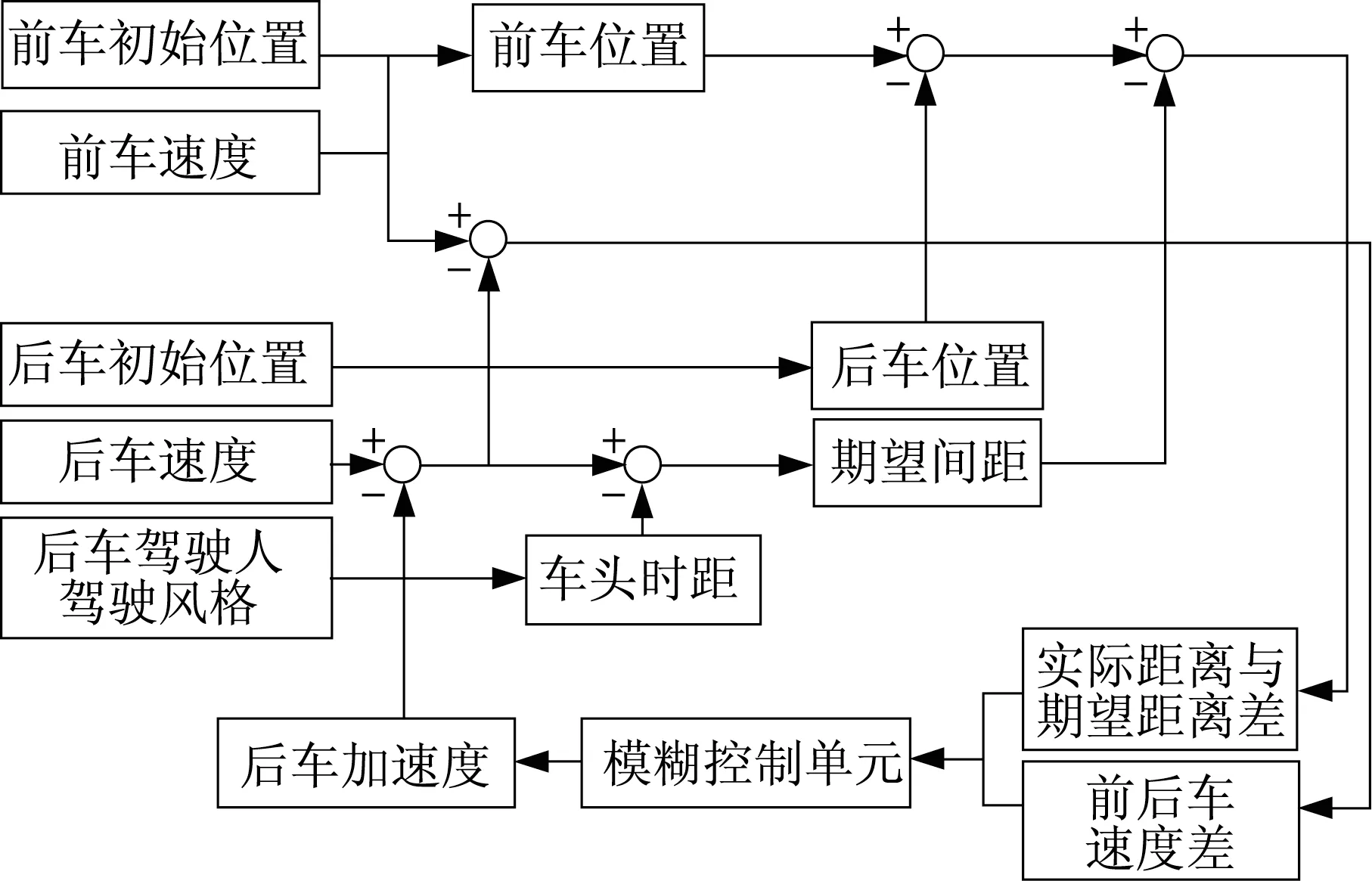
图8 基于模糊控制的跟驰模型结构Fig.8 Car-following model structure based on fuzzy control
3 Simulink数值分析
利用MATLAB 的Simulink 进行数值分析,设置模糊控制系统过程,并根据模糊规则设置输入、输出参数隶属度函数,建立与对应的跟驰模块如图9所示,模型计算步长设为1 s。

图9 模糊控制系统Simulink模块图Fig.9 Simulink module diagram of fuzzy control system
输入前车的速度和实际位置,后车的初始速度、位置和驾驶风格,对于不同驾驶风格,根据表3 判断,得到不同的期望车头时距,输入对应的参数。
在Simulink中分别得到三种类型驾驶风格的位移-时间图,如图10~12所示,将模型得到的后车位移与真实数据进行对比分析。同时分别得到三种类型驾驶风格的速度-时间图,如图13~15所示,将模型得到的后车速度与真实数据进行对比分析,并验证误差情况。
根据平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)对模型进行评价,其指标计算公式如下:

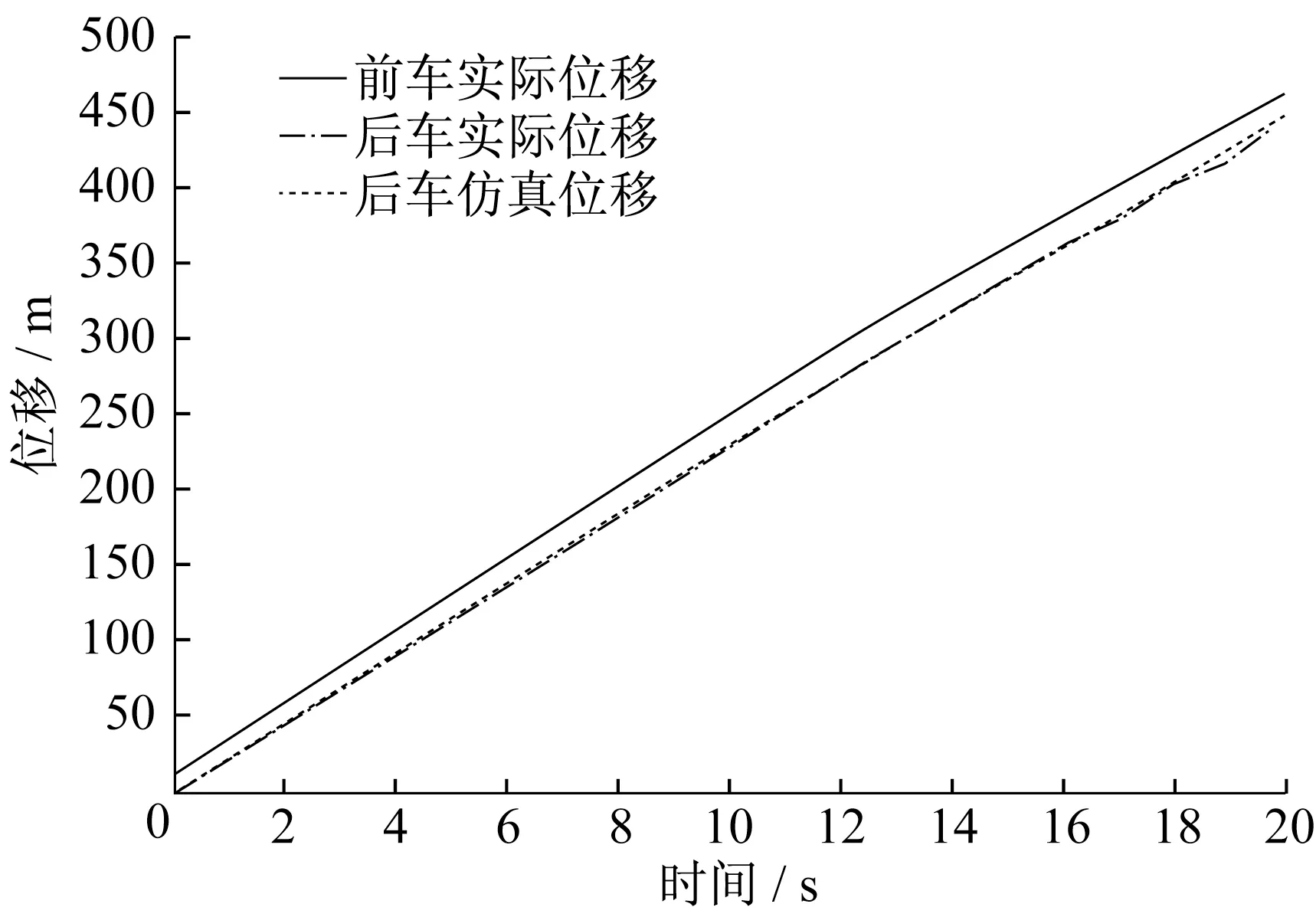
图10 激进型位移-时间关系Fig.10 Displacement-time relationship of angry driving style
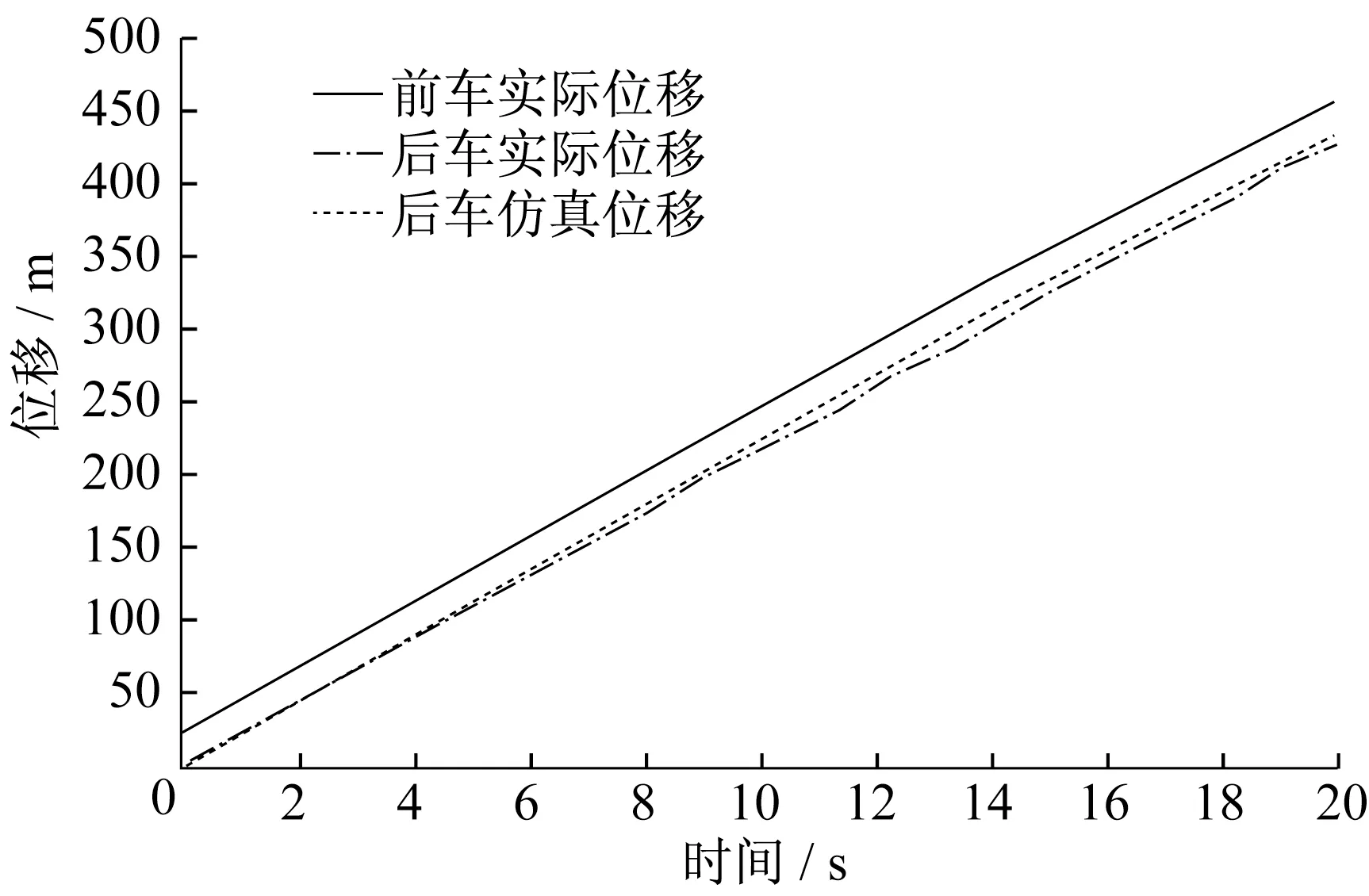
图11 普通型位移-时间关系Fig.11 Displacement-time relationship of normal driving style
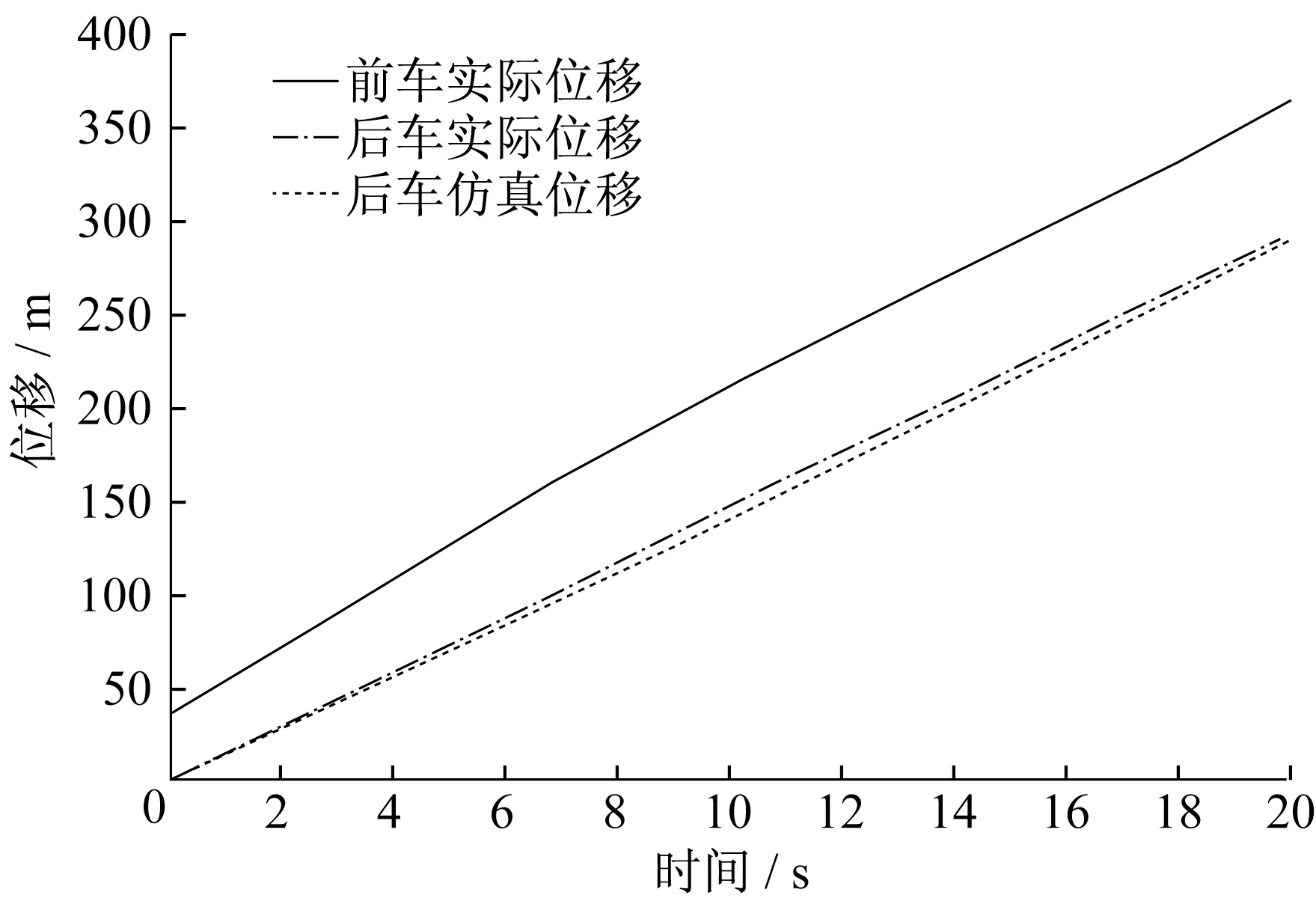
图12 保守型位移-时间关系Fig.12 Displacement-time relationship of conservative driving style
式中:i为样本编号;n为样本总量;yi为第i个样本实际数据i为第i个样本仿真数据;
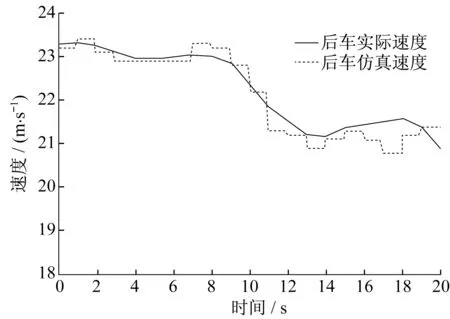
图13 激进型速度-时间关系Fig.13 Velocity-time relationship of angry driving style
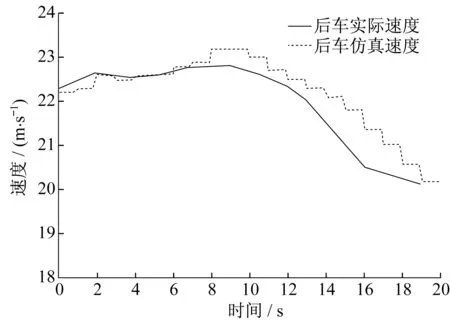
图14 普通型速度-时间关系Fig.14 Velocity-time relationship of normal driving style

图15 保守型速度-时间关系Fig.15 Velocity-time relationship of conservative driving style
对三类驾驶风格的模型分别计算位移和速度的评价指标,结果见表5。
在不同出发间距、不同初始速度、不同驾驶风格的情况下,后车的跟驰状态不同,但模型的数值结果与自然驾驶实测的车辆轨迹相近,同时车速度变化较一致,数据的评价结果表示,模型的误差较小,说明本模型对于中国驾驶人有较好的适用性。

表5 模型评价结果Tab.5 Model evaluation results
4 结语
现有的基于模糊控制的跟驰模型,大多假设驾驶人行为方式相同,或是对不同驾驶人的行为风格进行分类,未考虑过同一驾驶人在不同状态下出现驾驶风格的差异,且在划分隶属函数论域时,缺乏自然驾驶数据的分析。
本文利用中国驾驶人自然驾驶数据,按驾驶风格,对快速路自然驾驶跟驰片段的驾驶行为进行分类。通过数据分析发现,驾驶风格对跟驰车头时距的影响显著,并可以拟合为三类驾驶风格。在此基础上,利用真实数据划分输入变量的论域,建立相应的三角隶属度函数,对模糊控制规则表进行调整优化,建立了基于模糊控制的跟驰模型。通过验证与实际数据对比表明,该模型能够准确地描述不同驾驶风格的驾驶人跟驰过程。
由于自然驾驶数据样本数量有限,后期可以增加更多的验证,同时由于各国驾驶风格类型不同,若将该模型应用于国外情况时,需要进一步深入研究。

