基于贝塞尔曲线的卵石骨料混凝土细观模型
潘子超,李天华,阮 欣
(1. 同济大学土木工程学院,上海200092;2. 新疆城建试验检测有限公司,新疆乌鲁木齐830000)
在细观尺度上,混凝土是一种由水泥砂浆、骨料和界面层构成的复合材料。其中,骨料包含碎石和卵石两种类型。碎石骨料的特点是:多棱角、表面粗糙度大、与水泥砂浆之间的粘结力强。卵石骨料的特点是:形状较为规则、表面圆滑、与水泥砂浆之间的粘结力弱。由于上述两种骨料的特点,在配合比相同的条件下,碎石混凝土强度一般高于卵石骨料。然而,卵石混凝土也具有更好的流动性和抗断裂性能[1]等优点,且卵石骨料不需要复杂的生产线。我国的卵石资源丰富,尤其在河道、山谷和戈壁等局部地区。因此,尽管在强度等方面不及碎石混凝土,卵石骨料仍具有一定的应用价值。
为了考虑不同类型的骨料对混凝土强度、耐久等各种性能的影响,需要在细观尺度上开展相应的研究。这些研究的前提是构建混凝土的细观模型。目前,针对碎石骨料混凝土细观模型已有很多研究成果。其中,Wang等[2]在极坐标系中建立了随机多边形骨料的生成算法及基于波前法的网格划分方法。高政国和刘光廷[3]提出了基于生长法的凸多边形随机骨料的生成算法,并给出了凸多边形生成条件和方式。同样基于生长法,孙立国等[4]为解决大体积全级配或三级配混凝土细观模型的构建问题,提出了一种新的高效骨料投放算法。Pan等[5]建立了基于切割法的凸多边形随机骨料模型。李建波等[6]突破了传统凸形骨料的限制,建立了一种随机凹凸型骨料模型,使细观模型更接近于混凝土试件断面的实际情况。为了增加骨料形状的真实性,一些学者采用图像处理的方式来获取真实骨料的形状。付兵等[7]采用图像处理方法从真实混凝土试件的断面中提取骨料形状建立骨料库,并从数据库中随机选出骨料建立细观模型。Garboczi[8]将球面调和函数应用于骨料形状的模拟,通过对电子计算机断层扫描(computed tomography,CT)图像的矢量化建立骨料模型。这种方法具有很高的真实性,但效率很低。上述研究的一个共性是采用随机多边形或多面体模拟骨料形状。这些方法不适用于卵石骨料。考虑到卵石具有圆滑表面的特性,文献中多采用圆形、椭圆形来模拟其形状[9-10],但这种假定过于简单。
因此,本文首先建立一种基于贝塞尔曲线的卵石骨料混凝土细观模型,引入骨料长宽比和半径变异度两个参数控制卵石骨料的形状。其次,通过图像处理方法对1 000多个真实卵石骨料的分析提取骨料长宽比和半径变异度的随机分布特性。在此基础上,针对物质传输问题,选择迂曲度表征骨料对物质传输速率的影响,建立基于Floyd-Warshall动态规划算法的迂曲度计算过程。最后,通过参数分析,研究卵石和碎石骨料混凝土细观模型在迂曲度上的不同。
1 卵石骨料模型
卵石骨料由于没有明显的棱角,可通过对多边形顶点进行光滑处理来获得骨料的形状。这个步骤模拟了碎石在自然环境中不断磨蚀而形成卵石的过程。借助于贝塞尔曲线,可将这种磨蚀过程量化,从而得到不同光滑程度的带有一定曲率的多边形(以下简称曲率多边形)。
1.1 初始多边形
根据骨料的级配在极坐标中生成一个初始多边形。为此,首先随机确定多边形的顶点数N0。N0的取值范围为Nmin~Nmax。其中,Nmin和Nmax为人为设定的最小和最大多边形顶点数。其次,将整个坐标系沿着角度方向划分为N0个相同的区域,在每一个区域,随机生成多边形顶点的极坐标Pi(αi,ri)。其中,αi和ri分别为多边形第i个顶点(i=1,2,…,N0)在极坐标系统中的极角和极径。αi和ri的取值范围分别为2π(i-1)/N0~2πi/N0和r0(1-β)~r0(1+β)。其中,r0为与多边形等面积的基准圆的半径,β反映了在极坐标下初始多边形各顶点半径的变异性程度(以下简称半径变异度)。图1给出了一个具有4个顶点(P1~P4)的初始多边形的生成实例。
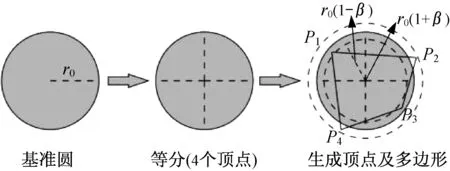
图1 初始多边形的生成过程Fig.1 Generation procedure of initial polygon
研究表明,骨料的长宽比对混凝土传质过程有一定的影响[9-10]。因此,当得到初始多边形后,需要对其进行拉伸,从而得到满足给定长宽比的多边形。为此,首先定义任意多边形的长宽比。对于图2 所示的多边形,选择任意一条边,确定多边形的外接矩形,其长度和宽度分别为li和hi(li>hi)。例如,图2中的多边形的边P4P5对应的外接矩形的长度和宽度分别为l45和h45。则多边形的长宽比为
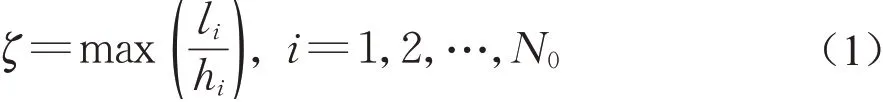

图2 多边形外接矩阵示意图Fig.2 Schematic diagram of polygonal circumscribed matrix
1.2 贝塞尔曲线
贝塞尔曲线(Bézier curve)是一种应用于二维图形应用程序的数学曲线,在矢量图形软件中可以精确地控制所绘曲线的形状。贝塞尔曲线的最大特点是,通过调整若干控制点的位置来确定曲线的弧度,从而将绘制曲线的问题转变为改变控制点的坐标,而后者在计算机中非常容易实现,且具有很高的精度。
贝塞尔曲线的复杂程度和灵活性随着控制点的个数增加而增加。一般使用较多的是具有3个和4个控制点的贝塞尔曲线,分别被称为二次和三次贝塞尔曲线。本文采用的是前者。
采用贝塞尔曲线建立卵石骨料模型的流程如下。得到如图1 所示的初始多边形后,针对多边形的每一个顶点,选择如图3所示的三个控制点P1、Q1和Q2。其中,P1为多边形的顶点,Q1和Q2分别位于P1所在的两个邻边上,δ 为一个在0~1.0 范围内的参数。同时,定义P1Q1的距离为
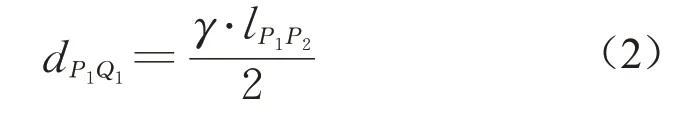
式中:γ为一个取值范围为0~1.0的参数。

图3 采用贝塞尔曲线对多边形顶点进行光滑处理Fig.3 Smoothing polygon vertex by Bézier curve
根据选择的三个控制点,贝塞尔曲线由图3 中B点的运动轨迹生成:

式中:P1、Q1和Q2分别为P1、Q1和Q2的坐标向量;δ为一个在0~1.0 范围内的参数;B(δ)为B 对应于δ的坐标向量。
当贝塞尔曲线生成后,根据多边形的凹凸情况,对初始多边形的形状进行调整。对于凸出的顶点,将位于贝塞尔曲线以外的部分从初始多边形中去除;对于凹入的顶点,增加贝塞尔曲线与初始多边形顶点围成的区域,分别如图3中P1点和P3点所示。
经贝塞尔曲线处理后的曲率多边形的光滑程度由式(2)中的参数γ控制。如图4所示,γ越大,光滑程度越高。但当γ>1.0 时,相邻的贝塞尔曲线相交,这是不允许的。因此,γ 的变化范围为0~1.0。γ=0 相当于初始多边形没有经过光滑处理。由于卵石骨料没有明显的棱边和棱角,因此通常情况下,可取γ=1。
1.3 侵入判定

图4 参数γ的取值对骨料形状光滑程度的影响Fig.4 Influence of parameter γ on smooth degree of aggregate shape
建立卵石骨料模型后,为了生成最终的混凝土细观模型,需要将卵石骨料逐个放入到水泥砂浆中。作为固体颗粒,骨料之间不能重合,因此在将骨料放入到水泥砂浆中,需要对每个骨料进行侵入判定。为此,首先将曲率多边形的贝塞尔曲线部分离散为由一系列密集点组成的线段。其次,针对每一个点,判断其是否在另一个曲率多边形内。这里采用了如下方法:①从一个点生成任意一条射线;②对曲率多边形的每一条边进行遍历;③对每一条边,判断其与射线是否存在交点,注意到此时的边是线段,而不是直线;④如果多边形与射线的交点总数为奇数,则该点在多边形内部。
1.2 节提出的方法同时适用于凹形和凸形多边形。如果有任意一个点位于另一个曲率多边形内,则存在侵入现象,需要重新生成曲率多边形的位置。按照上述骨料投放算法,图5a给出了一个采用贝塞尔曲线模拟得到的卵石骨料混凝土细观模型的示例。作为对比,图5b给出了一个具有相同面积分数和长宽比的碎石骨料混凝土细观模型。可以看出,本文提出的采用贝塞尔曲线的方法可以较为真实地模拟出具有光滑边缘的卵石骨料。
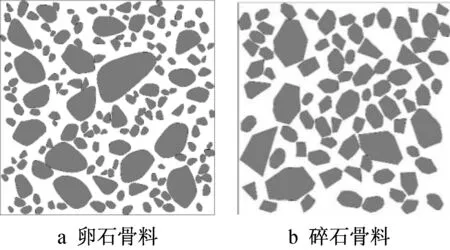
图5 卵石和碎石骨料混凝土细观模型示例Fig.5 Examples of concrete mesoscopic model by pebble and crushed-stone aggregates
2 骨料参数
2.1 参数获取方法
在1.2 和1.3 节提出的采用贝塞尔曲线生成卵石骨料的方法中,骨料的长宽比(ζ)和半径变异度(β)是影响骨料形状的两个最重要的参数。为了保证所生成的骨料形状与实际情况相符,根据真实骨料的形状,采用图像分析方法获得这两个参数的统计规律。为此,收集了新疆乌鲁木齐市常见的卵石骨料1 000余个。骨料的级配曲线如图6所示。

图6 卵石骨料级配曲线Fig.6 Gradation curve of pebble aggregate
首先,采用二值化、连通区域标记[11]、Canny 边缘检测[12]和凸包等算法获取每个骨料的边缘,如图7所示,并找到所有可能的骨料外接多边形。基于这些外接多边形和式(1)的定义,可以得到骨料的长宽比(ζ)。其次,根据边缘像素点的位置,求出骨料的中心点坐标和各像素点到中心点的距离,得到最大值rm和最小值ri,并计算出与骨料面积相等的基准圆的半径r0。在此基础上,可得到半径变异度:


图7 真实骨料二维投影图像的二值化和分离Fig.7 Binarization and segmentation of two-dimensional projection image of real aggregates
2.2 随机概率分布
根据1.1 和2.1 小节的方法得到每个卵石骨料的长宽比(ζ)和半径变异度(β),并将这些结果以直方图的形式给出,分别如图8 和图9 所示。可以看出,ζ和β的取值分别集中在1.0~2.0和0.2~0.5之间。为了便于在生成混凝土细观模型过程中确定每个骨料的ζ 和β,将这两个参数视为随机变量,分别选择正态分布、对数正态分布和一般极值分布(GEV)对其进行拟合。根据拟合结果计算如下均方根误差(root mean square error,RMSE):
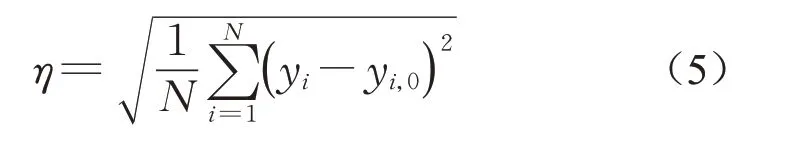
式中:yi,0和yi分别为原值和拟合值;N 为数据点个数。计算结果如表1所示。可见,ζ和β的分布类型均最接近一般极值分布。

图8 骨料长宽比(ζ)的直方图Fig.8 Histogram of aspect ratio of aggregate (ζ)

图9 骨料半径变异度(β)的直方图Fig.9 Histogram of radius variability of aggregate(β)

表1 根据均方根误差得到的随机分布类型识别结果Tab.1 Identification results of random distribution type based on RMSE
得到ζ和β的随机分布类型及参数后,在生成混凝土细观模型时,将根据对应的随机分布进行抽样,得到每一个骨料的ζ和β的取值。
3 细观模型的迂曲度
3.1 迂曲度的定义和计算方法
水泥的水化过程在生成水化产物的同时,也在水泥浆中形成了复杂的孔隙结构。各类物质在孔隙中的传输路径受到孔径大小、走向和连通性等因素的限制而出现扭曲,如图10所示。

图10 微观尺度上混凝土孔隙结构的迂曲度[13]Fig.10 Tortuosity of pore structure of concrete at micro-scale[13]
因此,物质的传输速率与孔隙结构的迂曲程度密切相关,但目前尚没有针对两者定量关系的模型。Ishida等[13]在研究氯离子扩散的问题中,认为氯离子的扩散通量与迂曲度成反比。而Al-Raoush 等人[14]认为物质扩散系数与迂曲度的平方成反比。然而,不论是哪一种模型,可以肯定的是,物质的传输速率随着迂曲度的增加而降低。因此,迂曲度在一定程度上可以定性地反映物质在混凝土中传输的难易程度。
尽管迂曲度最初是在微观尺度上定义的,但根据其基本思想,通过将微观尺度上的水泥水化产物和孔隙结构均质化为水泥浆,可以定义细观尺度上的迂曲度[15]:

式中:lme和lma分别为细观和宏观尺度上的最短物质传输路径。
根据迂曲度的定义,可采用Floyd-Warshall动态规划算法计算不同侵蚀深度处的迂曲度[16]。为了使用Floyd-Warshall算法,需要将细观模型离散成像素密度为n2的图形。因此,像素密度的选择对迂曲度的计算结果存在影响。针对这一问题,进行了一个典型算例的分析。模型的大小为0.1×0.1m2,骨料面积分数为0.4,级配曲线如图11所示,骨料光滑度为0.5,骨料长宽比和半径变异度分别根据图8 和图9 进行抽样。根据这些参数,首先生成混凝土细观模型。然后,选择像素密度n=10~80,计算出各像素密度条件下细观模型的迂曲度,如图11 所示。从图中可以看出,随着像素密度的增加,迂曲度逐渐降低,当像素密度达到n=50时,迂曲度随像素密度的变化已经很小了。由于Floyd-Warshall 算法的时间复杂度为O(n3),计算时长将随着n 显著增加,因此在后续分析中将选择n=50,不再采用更高的像素密度,以提高计算效率。
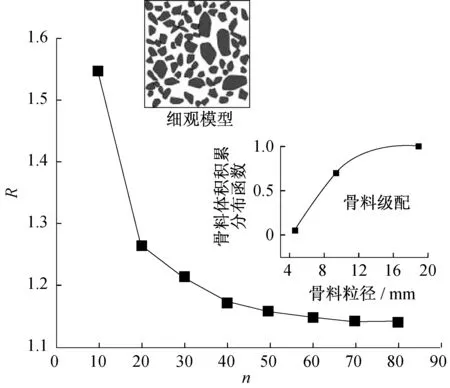
图11 迂曲度与像素密度的关系Fig.11 Relationship between tortuosity and pixel density
3.2 分析结果
3.2.1 计算参数
根据3.1小节中迂曲度的定义和计算方法,对比了卵石和碎石骨料混凝土细观模型的迂曲度之间的差异。分析工况中的参数取值如表2所示。其中,根据《建设用卵石、碎石》(GB/T 14685—2011)[17]中的规定,选择了三种具有不同最大骨料粒径的级配,如图12所示。为了降低细观模型的随机性对计算结果的影响,每个工况包含了100次模拟,并计算出迂曲度的平均值。其中,碎石骨料的模拟方法可参考文献[5]。
3.2.2 骨料含量
骨料含量对混凝土细观模型迂曲度的影响如图13所示。可以看出,随着骨料含量的增加,卵石和碎石骨料细观模型的迂曲度均随之增大,当骨料面积分数从0.3增加至0.5时,两种骨料细观模型的迂曲度分别从1.119和1.121增大至1.174和1.200,增大幅度分别为4.92%和7.05%。这个结果可以通过随机行走的理论来解释。随着骨料含量的增加,细观模型中的骨料数目增加,骨料之间的平均距离减小。从暴露面侵入的物质粒子在向模型内部运动的过程中有更高的概率碰到骨料,从而改变其运动方向。因此,在统计意义上,当这些物质的粒子运动至特定的深度时,实际路径的长度要大于骨料含量较小的情况。

表2 细观模型迂曲度参数分析工况Tab.2 Parametric analysis conditions of mesoscopic model tortuosity model tortuosity
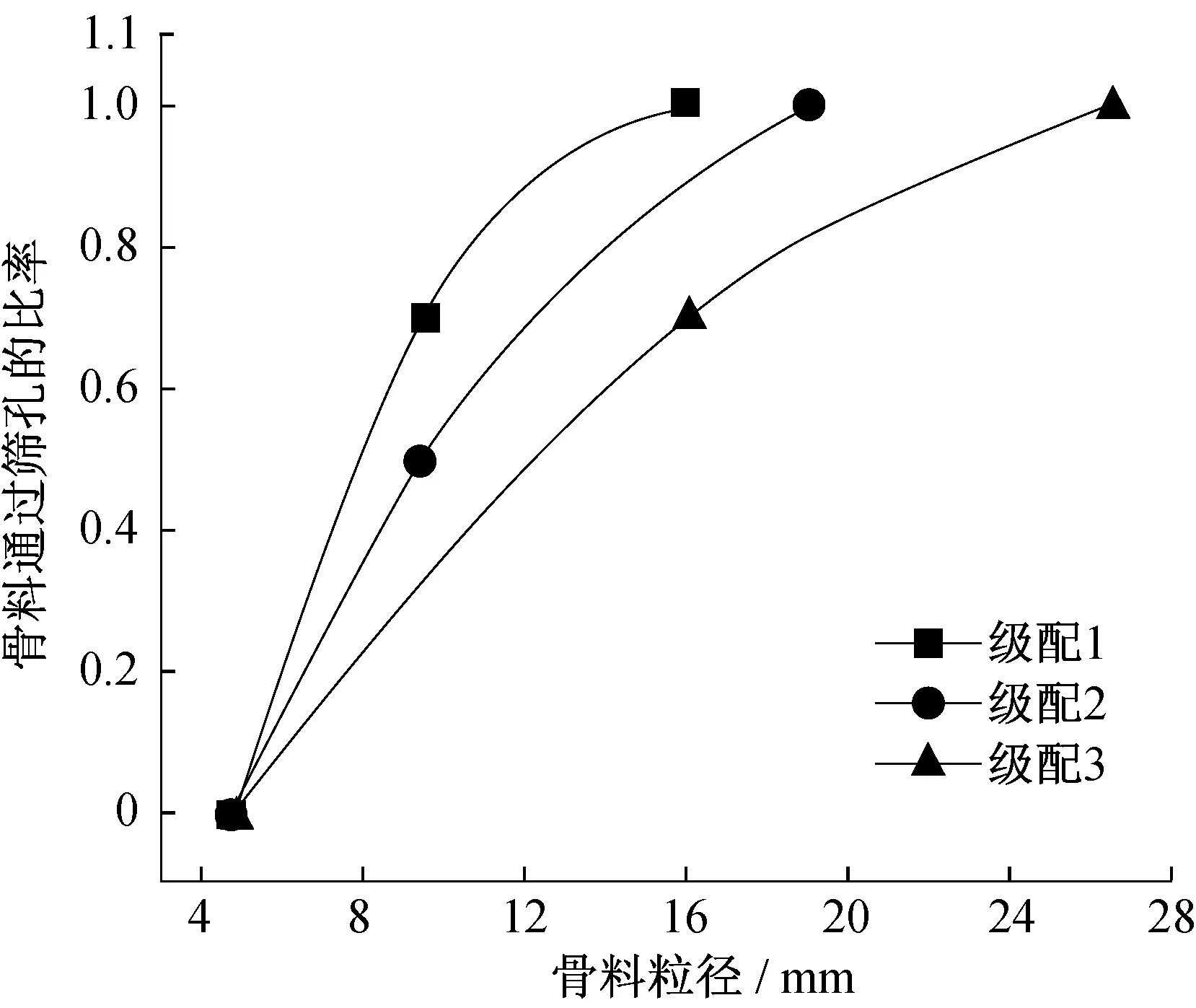
图12 混凝土粗骨料级配曲线Fig.12 Gradation curveof coarse aggregate of concrete

图13 不同骨料含量下卵石和碎石骨料混凝土细观模型的迂曲度比较Fig.13 Comparison of mesoscopic model tortuosity between concrete made by pebble and crushed-stone aggregates with different aggregate contents
此外,当骨料含量一定时,卵石骨料细观模型的迂曲度小于碎石骨料,并且两者的差别随着骨料含量的增加而增大,当骨料面积分数从0.3增加至0.5时,两种骨料细观模型迂曲度的差别分别从0.055增大至0.079,变化幅度为43.64%。这一结果表明,卵石骨料阻碍物质传输的能力小于碎石骨料。其主要原因是碎石骨料具有明显的棱边。当粒子(水分子及各类离子等)运动到骨料表面时,由于骨料的不可渗透性,粒子被迫沿着骨料表面绕流,传输路径出现较大程度的扭曲。而卵石骨料表面光滑,会在细观模型内部形成流线型的传输路径,对粒子运动方向的改变程度显著低于碎石骨料。因此,卵石骨料细观模型的迂曲度小于碎石骨料。
3.2.3 骨料级配
骨料级配对混凝土细观模型迂曲度的影响如图14所示。可以看出,骨料级配对迂曲度没有明显的影响。随着级配中最大骨料粒径的增大,卵石和碎石骨料细观模型的迂曲度均随之减小,但幅度很小。例如,当骨料面积分数为0.4时,对于级配1和3,卵石和碎石骨料细观模型的迂曲度从1.143和1.150减小至1.136和1.141,减小幅度仅为0.61%和0.78%。而当骨料面积分数为0.5时,这一幅度为1.10%和1.08%。此外,根据图14中的结果还可以发现,两种骨料细观模型迂曲度的差别并不随级配的改变而出现明显的变化,但会随着骨料面积分数的增加而增大。例如,当骨料面积分数为0.4增大至0.5时,对应于级配1和3的两种骨料细观模型迂曲度的差别分别从0.007和0.005增大至0.022和0.022。但总体上看,骨料级配对细观模型迂曲度的影响不及骨料面积分数明显。
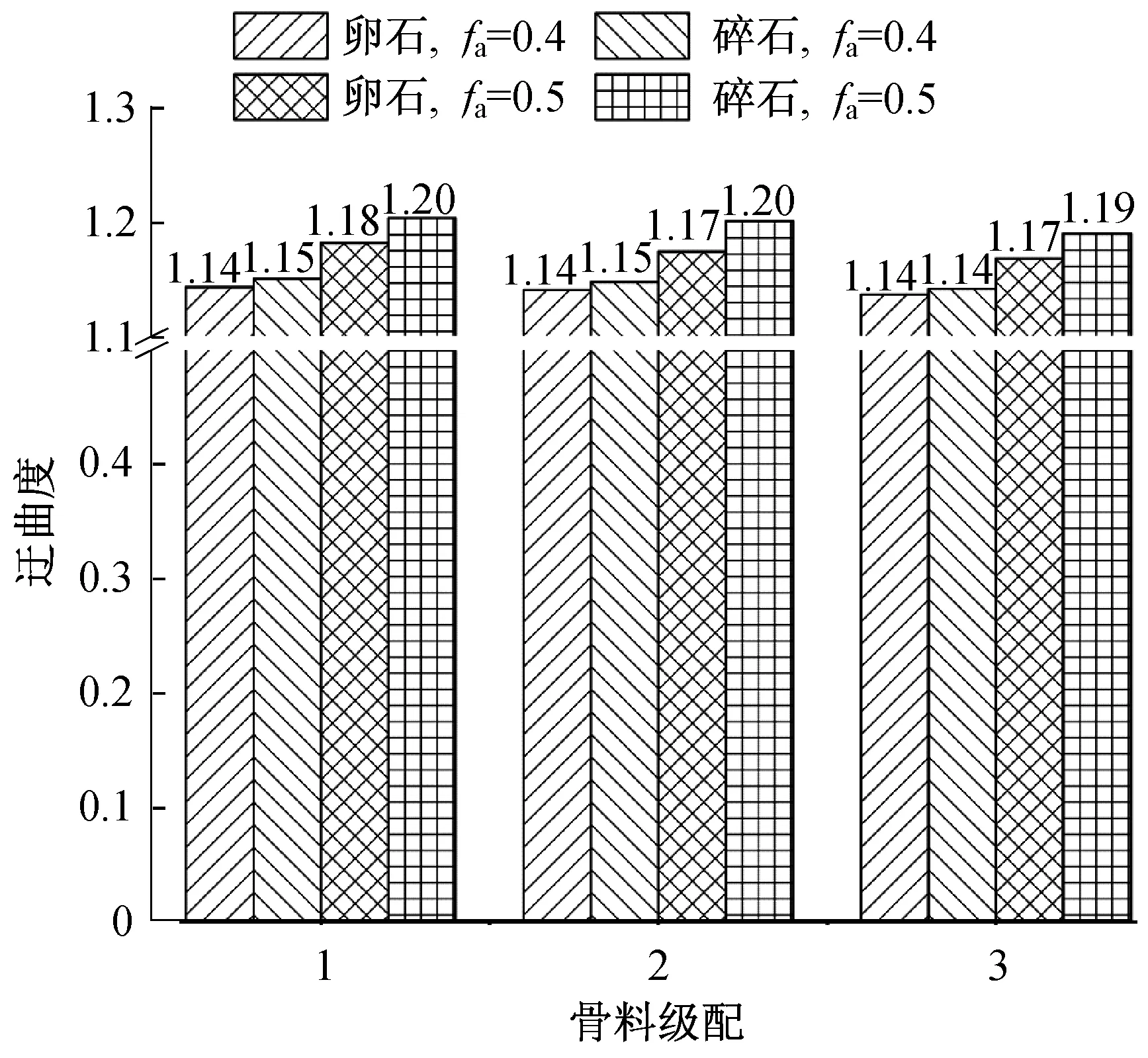
图14 不同级配下卵石和碎石骨料混凝土细观模型的迂曲度比较Fig.14 Comparison of mesoscopic model tortuosity between concrete made by pebble and crushed-stone aggregates with different gradations
4 结论
本文建立了一种基于贝塞尔曲线的卵石骨料模型,并通过图像处理方法获取了真实卵石骨料的长宽比和半径变异度两个重要参数的取值。在此基础上,进一步开展了细观模型迂曲度的研究,建立了基于Floyd-Warshall动态规划算法的迂曲度计算过程。最后,分析了不同骨料含量和级配条件下,卵石和碎石骨料混凝土细观模型迂曲度之间的差别。根据分析结果,可得如下结论:
(1)贝塞尔曲线可以有效地模拟具有光滑边缘的卵石骨料,进而建立基于卵石骨料的混凝土细观模型;
(2)对真实卵石骨料形状的图像处理结果表明,骨料长宽比和半径变异度均服从一般极值分布,前者取值大多在1.0~2.0 之间,后者取值大多在0.2~0.5之间;
(3)当骨料含量和级配一定时,卵石骨料细观模型的迂曲度小于碎石骨料;卵石和碎石骨料细观模型的迂曲度均随着骨料含量的增加而增大,且两者的差别随着骨料含量的增加而增大;
(4)随着骨料级配中最大骨料粒径的增大,卵石和碎石骨料细观模型的迂曲度均随之减小,但幅度很小,且卵石和碎石骨料细观模型迂曲度的差别不随骨料级配的改变而出现明显的变化。

