可拆卸性产品的闭环物流网络设计模型

周利民，陈秋妮，李 静，朱广娇 ZHOU Limin, CHEN Qiuni, LI Jing, ZHU Guangjiao

（昆明理工大学 管理与经济学院，云南 昆明650093）

0 引 言

随着经济进入新常态，越来越多的国家关注废旧产品的回收问题。我国在2008 年颁布了《废弃电器电子产品回收处理管理条例》，要求企业对废旧产品进行回收。回收的产品不仅数量增加，还有类型增加，比如：电器、电子、家具等。然而拆卸是回收和重新利用的前提，为了更好达到保护环境，减少企业成本的目的，认真研究可拆卸产品是必要的[1]。可拆卸产品的价值创造与常规的商品不同，常规商品一般从生产商经各种经销商传递至消费者手中，实现创造经济效益，而可拆卸产品的回收与利用需要个人或集体手中逆向传递至生产商或材料商手中。拆卸后的零件使用范围比较具有针对性，一般只有在生产商或材料商手中才能创造价值。所以可拆卸商品的物流网络设计模型问题与常规商品有较大的差异。构建一套完整的正向供应与逆向回收的物流运输链并对运输链上的各类商家都可以创造额外的经济效益。

近年来，很多国内外学者对闭环供应链的物流设施选址、车辆路径优化以及库存问题进行了深入的研究。但在现有的大多数文献中，选址—路径优化问题主要用来研究静态闭环供应链的优化[2]，然而在社会经济环境的变化、环境污染加重的情况下，越来越多的研究学者倾向于考虑产品类型的差异，如废旧汽车、废旧电子产品、可拆卸产品等。Blanc[3]建立废旧汽车系统网络模型，该模型运用路径优化的方法计算废旧汽车回收的运输成本，并采用混合整数规划方法来确定最佳的废旧汽车拆解中心和库存数量；周虹[4]建立了一种包含多产品、有能力限制的闭环供应链的混合整数规划模型，以制造商为核心，同时对不同收益情况下产品的自营与外包的数量进行了分析，使可拆卸产品逆向网络的总体利润最大。李昌兵[5]将正向配送和逆向回收相结合来考虑选址—路径优化问题，并引入库存限制和库存成本惩罚，使物流网络布局问题更加优化。许民利[6]构建回收产品可拆卸的多周期混合制造网络模型，综合考虑物流网络中正逆向物流的选址—路径问题，将可拆卸产品的部分零件进行回收利用。李伯棠[7]考虑物流成本和碳排放量这两个因素，建立了闭环物流网络混合线性规划模型，来解决模糊环境下的低碳闭环物流网络设计问题，最后采用遗传算法对模型进行验证。Davenport T H, et al[8-10]根据不同的选址问题，采取不同的算法去解决，运输配送问题，丰富了路径规划问题的研究成果。张鑫等人[11]基于可信性理论的两个约束，以闭环供应链物流网络总成本最小，建立起目标和约束条件双重模糊的闭环物流网络模糊规划模型。总体而言，以上文献研究存在两点不足：一是关于闭环供应链的设施—路径优化研究，大多数集中于废旧产品的研究，并没有把废旧产品具体化。二是在以往关于可拆卸产品的研究中，很少有关于它的设施—路径研究，更多是产品的可拆卸性的设计。

综上所述，针对现有文献中缺失以可拆卸产品为研究对象的闭环物流网络设计问题的研究，建立以回收产品为可拆卸产品，将检测拆分中心考虑在模型之内的总费用最小模型，以闭环供应链系统的总成本最小为目的，来确定系统上各设施的位置、数量以及物流分配。可拆卸产品的再利用需要回收、拆解、分类等多步处理，分类后的产品中包含零件、原材料、报废品等多个部分，所以可拆卸产品的闭环物流网络设计模型中需要将逆向的多级物流与正向的供应物流进行优化整合。

1 问题描述

可拆卸产品的闭环供应链是由正向供应和逆向回收两部分组成，其中正向供应部分就是传统的生产销售物流，而逆向回收却是一个新兴的研究领域。本文针对可拆卸产品闭环供应链而言，将整个闭环供应链系统运作过程如图1 所示。从正向供应的物流运作来看，先由生产商从供应商那购买原材料，生产商对其进行生产后，将产品运往分销中心，销售商从分销中心那拿货，再销售给消费者。从逆向物流的运作过程来看，消费者将废旧产品（可拆卸产品） 以低于购买价的方式卖给销售回收商，而销售回收商把回收到的可拆卸产品，运往回收站，此时回收站会对可拆卸产品进行区分，可以拆卸的直接运往检测拆分中心，不可以拆卸的直接报废。拆卸检测中心先对可拆卸产品进行检测，然后进行拆卸，若拆卸的是零配件，直接运往生产商，若是原材料，直接运往供应商。

图1 闭环供应链流程图

2 模型构建

2.1 模型假设

为了便于模型的建立做出以下假设：

（1） 商品的运输过程均按照供应链中所规划的路径进行，不存在越级运输的情况。

（2） 生产商的产品具有一定的稳定性，即可拆卸商品在回收过程中，商品的报废率与拆解成原料与零配件的比例不会出现大的波动。

（3） 由于商品具有可回收的属性，最后一级的销售商同时承担第一级的回收商，商品的使用与回收时间没有限制，但仅

回收生产商制造的商品，与本供应链无关的商品不予处理。

（4） 模型计算的最终结果是使整个闭环供应链的运行成本最低，只进行每个环节的成本计算，对该成本的承担方案不进行设计。

（5） 每个环节产品的运输成本只与运输距离与货运量有关，不考虑特殊情况造成的运输成本增加。

（6） 经回收站与检测拆分中心产生的原材料与零配件，性质稳定均达到产品的相关要求。

（7） 闭环供应链中所涉及的各个环节均具备一定的库存能力，库存成本的投入均为已知量。

（8） 产品可全部拆卸为零件，生产商与销售商对每个零件的价值均为已知。

2.2 符号说明

（1） 模型参数

Q：可拆卸产品供应链的最小费用；Q1：供应链的运输费用；Q2：供应链的建设投入；Q3：拆解中心的运行维护费用；i：供应商的集合，i∈I；j：生产商的集合，j∈J；k：分销商的集合，k∈K；l：零售商的集合，l∈L；m：回收中心可选地点的集合，m∈M；n: 检测拆分中心可选地点的集合，n∈N；Wm：回收站的建设投入；Wn：检测拆分中心的建设投入；Sij：供应商与生产商之间的距离；Sjk：生产商与分销商之间的距离；：零售商与分销商间的距离；：零售商与回收中心之间的距离；Smn：回收中心与检测拆分中心的距离；Sni：检测拆分中心与供应商之间的距离；Snj：检测拆分中心与生产商之间的距离；Dij：供应商与生产商之间的单位运输成本；Djk：生产商与分销商之间的单位运输成本；：零售商与分销商之间的单位运输成本；：零售商与回收中心之间的单位运输成本；Dmn：回收中心与检测拆分中心的单位运输成本；Dni：检测拆分中心与供应商之间的单位运输成本；Dnj：检测拆分中心与生产商之间的单位运输成本；Vij：供应商与生产商之间的运输量；Vjk：生产商与分销商之间的运输量；：分销商与零售商之间的运输量；：零售商与回收中心之间的运输量；Vmn：回收中心与检测拆分中心的运输量；Vni：检测拆分中心与供应商之间的运输量；Vnj：检测拆分中心与生产商之间的运输量；Ac：单周期c零件的拆解数量，c∈（1,2,3,4…,n ）；Ae：单周期原材料e的拆解重量，e∈（1,2,3,4…,n）；Bc：拆解出零件c需要的成本；Be：拆解出单位重量e需要的成本。

（2） 决策变量

：回收站m是否将产品运往检测拆分中心n；：检测拆分中心是否将原料运往供应商i；：检测拆分中心是否将原料运往生产商j；Xm：是否在m地开设回收中心；Xn：是否在n地开设检测拆分中心。

2.3 模型的建立

本文以可拆卸产品为对象，研究其在闭环供应链中的选址与路径最小费用。包括运输费用、建设投入费用以及运营费用。可拆卸产品的闭环供应链最小的建设成本为链上各组成部分最小成本之和，其目标函数Q如下：

在模型中，为了使目标函数Q达到最小，需要将运输费用Q1、建设投入费用Q2以及检测拆分中心的运营费用Q3之和达到最小。

（1） 运输费用Q1

在模型中，式（2） 阐述了参与闭环供应链的各个主体间的运输费用关系。式（3） 叙述了生产商、分销商与零售商间的距离关系，即生产商到分销中心的距离应大于分销中心到零售商的距离。式（4） 对供应商、生产商、分销商以及零售商两两之间的单位运输成本的关系。式（5） 中限制了供应商到生产商的运输量大于生产商到分销商的运输量。式（6） 限制了生产商到分销商的运输量等于各零售商到分销商的运输量之和。

（2） 回收中心与检测拆分中心建设投入费用Q2

回收链的构建一般以较为完善的正向供应销售链为基础[11]，因此本文在闭环供应链中只考虑回收中心与检测拆分中心的建设投入费用。式（8） 限制了回收中心与检测拆分中心的投入成本。式（9）、式（10） 是回收中心与检测拆分中心的选址决策变量。

（3） 检测拆分中心的运营费用Q3

在闭环供应链构建过程中，除运输与建设费用外，检测拆分中心的日常运营也需要资金维持。拆分中心的运营费用主要由零配件与原材料的拆分成本构成。

式（11） 为检测拆分中心的拆分零件与原材料的运营费用。式（12） 表明零售商回收可拆卸产品数量多于零件与原材料之和。式（13） 表明回收中心运往检测拆分中心的可拆卸产品可全部拆分为零件和原材料。式（14） 回收站m是否将回收的可拆卸产品运往检测拆分中心n。式（15） 检测拆分中心是否将原材料运往供应商i。式（16） 检测拆分中心是否将零配件运往生产商j。式（17）、式（18） 表明零件与原材料的拆分成本大于零。

3 模型分析与实例验证

3.1 模型分析

可拆卸性与具有回收价值的产品是使用本模型的前提，对于一次性产品、消耗品与具有一定使用寿命的产品并不适用该模型。如食品、生活用品及电子消耗品等产品，由于其具有产品种类多，回收后无质量保证，回收价值小于回收成本等缺点，并不适合拆解回收的物流模型。同时具备可拆解与可回收性质的商品在生活中的种类同样较多，如家电产品、电子产品中的电子原件、废旧汽车、大部分的金属制品、废旧家具中的木制品，实现回收再利用后，不仅可以在商品的制造环节节约成本的支出，还可以减轻对环境的污染。

把可拆卸产品的闭环供应链环节，分成供应链与回收链，供应链由材料供应商开始，至零售商结束。参与供应链各个商家间的运输关系如图2 所示。

图2 为正向供应环节存在的常规运输关系。由于生产商所需的原料一般由数家不同的材料供应商供应，同时一个材料供应商的材料也会被多个生产商所需要，所以供应商与生产商间为全覆盖交叉供应的关系。同理，分销商需要实现商品种类的富集，所以每个分销商需要接受各个生产商的货物，每个生产商也需要往各个分销商供货。在分销商实现商品种类富集后，零售商只需要在就近的分销商进行货物的批发即可，所以分销商与零售商的运输关系为一对多单线供应关系。

在回收链中，回收链由零售商开始，零售商作为商品销售的最末端，同时也是回收链的最始端，参与回收链各个商家运输关系如图3 所示。

图2 正向供应链运输关系

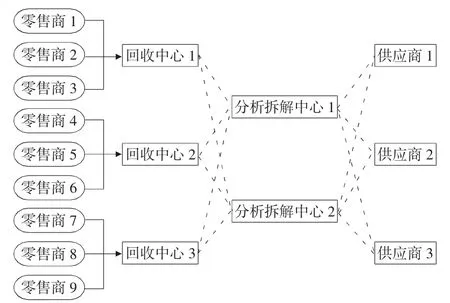
图3 回收链运输路径图

在逆向回收链关系中零售商会把回收的商品运输至最近的回收中心，所以各个零售商与回收中心的运输关系为确定关系。回收中心与分析拆解中心的连接线为虚线连接，每条虚线表示可能存在的运输关系，在实际回收过程中，虚线是否成为运输路径，要分析拆解中心是否可以处理当前的产品为主。如果处理产品过饱和，则转运给下一拆解中心进行拆解处理。同理分析拆解中心与供应商、生产商的关系也如此，分析拆解中心拆解出的零件的具体需求方需要按照供应商与生产商的需求来定，难以生成固定的输送路线。

3.2 实例分析

根据3.1 中对模型分析的结果来看，当一个商品正常销售时，关于该产品生产、配送路线已经基本成熟。但产品的回收链成熟时间要晚于正向配送链的时间。所以构建可拆卸产品的闭环供应链，一般是在正向供应链之后再构建逆向回收链，从而实现该产品的循环回收利用[12]。

以一种可拆卸回收产品为例，按照构建模型中的条件约束，对供应商、生产商、分销商与零售商进行位置选址。选址结果见图4。

按照模型要求在50 公里范围内随机生成供应商、生产商、分销商与零售商。各商家间的运输关系为模型分析中的运输关系，零售商的周围区域为其服务范围与回收产品的范围，按照分销商的位置可以把图中大致分为3 个大的消费区域。回收站的选择也大致锁定在这3 个范围内。从回收成本考虑回收站的位置为距离每个消费区域各个零售商距离总和最小点。回收站数量为3 个，具体位置如图5。

图4 供应链商家位置

图5 回收站位置

分析拆解中心的零件与原料需要供应给生产商与供应商，所以分析拆解的位置除考虑回收中心的位置外，还需要考虑距离供应商与制造商之间的位置。分析拆解中心的位置见图6。

基于路径最小原则，在图6 中给出了分析拆解中心的位置，根据计算结果，回收中心位置分别为（19.5,44.5 ）（31.1,24.4 ）（44.8,9.8 ），分析拆解中心的位置分别为（34.8,24.8 ）（25.5,18.8 ）。可以实现可拆卸性产品闭环供应链的供应。

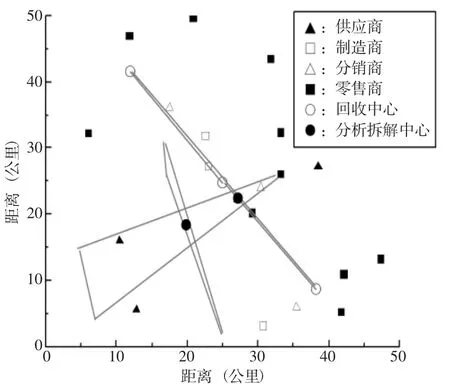
图6 分析拆解中心选址图

4 小 结

随着全球经济进入新常态，人们不仅关心社会经济利益，更关心对社会环境的影响，因此对物流模式提出了更高的要求，尤其是对可拆卸产品的闭环供应链的物流模式更是如此。传统的闭环供应链考虑正向配送和逆向回收两部分，而对于可拆卸产品的闭环物流网络设计是研究可拆卸产品最为重要的一步。本文针对单周期可拆卸产品的闭环供应链为研究对象，构建以供应商、生产商、分销商与销售商组成的正向供应链和以销售商、回收商、检测拆分中心、生产商与供应商组成的逆向回收链，对正逆向物流同时进行优化设计的问题研究。然后进行模型分析，案例分析，得到回收站和检测拆分中心的位置以及最短路径。本文构建的是单周期、单产品的模型，将来可以考虑多周期、多产品的闭环供应链物流网络设计模型。并且本文尚未对回收的可拆卸产品进行质量分级，这也可作为以后的研究方向。