基于自组织理论的津冀港口群协同演化研究

王 晶，王东磊，邓新娇 WANG Jing, WANG Donglei, DENG Xinjiao

（1. 燕山大学 经济管理学院，河北 秦皇岛066004；2. 燕山大学 区域经济发展研究中心，河北 秦皇岛066004）

0 引 言

随着经济区域化发展进程的推进，港口经济作为区域经济发展的重要组成部分，港口集群化发展已成港口发展的重要趋势，包含多个港口和交叉腹地的港口群系统逐渐成为研究热点。港口群系统是一个复杂的多主体动态适应系统，其演化过程受到系统内外部多种因素的影响，因此，研究港口群系统的协同演化需要综合考虑系统内外多种作用的影响，其演化过程具有动态性、复杂性和不稳定性。

国内外学者从多个角度对港口群系统演化进行了研究。国外有关港口群系统演化的研究较早，其中，Rimmer[1]发现了港口体系的分散化演化趋势；Slack[2]研究了港口体系演化的动力机制；Notteboom[3]在分析现代区域港口群腹地交叉、重合现象的前提下，提出了六阶段港口群空间演化模型；Gordon Wilmsmeier[4]等提出了影响港口系统从主要港口集中到去中心化演化过程的一些关键因素。国内港口群系统演化的相关研究起步较晚，主要集中在以下五个方面：（1） 运用系统动力学相关理论，建立动力学模型，分析港口群系统演化过程，如：刘沛[5]等研究了区域港口集疏运资源整合的内在动力；程佳佳[6]等分析了集装箱港口体系的演化过程，揭示了其动力机制。（2） 基于博弈论相关理论和方法，研究港口群演化过程中的竞合策略和协调机制，如：鲁渤[7]等建立了政府—港口演化博弈模型，提出了政府促进绿色港口建设的模式；赖成寿[8]等建立了港口竞合博弈双层规划模型，并引入“收益分配”、“合作成本”等参数构造非对称得益矩阵，分析了港口竞合演化路径。（3） 运用空间结构理论，对港口体系的空间结构演化过程进行研究，如：王绍卜[9]采用ArcGIS 空间自相关方法，研究了港口体系的空间结构及演化过程；赵旭[10]等分析了长时间序列下海上丝绸之路沿线港口体系集散趋势变化。（4） 利用复杂网络理论，研究港口网络演化问题，如：蹇令香[11]等根据港口群网络结构特征，通过构建加权网络演化模型，揭示了其演化特征；黎燕[12]运用改进的BA 模型，对我国重点建设的沿海港口网络进行模拟研究。（5） 以协同学理论为基础，运用动力学方法，研究港口群系统的演化，如：袁旭梅[13]等以自组织理论为基础，运用动力学方法，研究了港口群系统的演化动因，归纳了港口群系统演化的阶段性特征。

上述研究分别从不同角度对港口群系统的演化过程进行了有益探索。本文以自组织理论为基础，结合复杂性和稳定性分析，综合考虑系统内部的自组织和外部环境的他组织作用对演化过程的影响，引入竞争合作系数和政府干预系数，建立演化模型，得到不同条件下系统的演化趋势和结果，并进行分析讨论。

1 津冀港口群系统协同演化模型的建立

1.1 变量定义。津冀港口群系统是一个由多个港口及交叉腹地组成的多主体的复杂适应系统，其动态演化过程具有复杂性和不稳定性，受到系统内外部多种影响因素的制约。根据对津冀港口群系统的自组织与他组织演化条件的分析，模型变量设计如下：xi（t）：子系统i的盈利能力（i=1,2,…,n），xi0是子系统i的初始盈利能力；Ri：子系统i在一定条件下和特定发展阶段内盈利能力的固有增长率；Mi：子系统i依靠自身条件独立发展的最大盈利能力；αij：子系统i与子系统j之间的竞争合作系数；Gi：政府对子系统i演化的干预系数。

1.2 系统假设。津冀港口群系统协同演化模型旨在得到各港口子系统盈利能力xi在其他变量不同的情况下的演化趋势及结果，为严格控制变量，得到较可靠的仿真结果，对模型做出以下假设：

假设1：各子系统的盈利能力xi（）

t是时间t的连续可微函数。

假设2：各子系统的盈利能力的固有增长率Ri＞0，且在一定的发展阶段内不变。

假设3：各子系统的最大盈利能力Mi，是在一定腹地资源的限制下，交通集疏运条件、物流设施条件和港口自然条件等的约束下独立发展所能达到的最高盈利水平。

假设4：竞争合作系数αij表示各子系统之间竞争合作的倾向，将αij的取值范围设定为-1≤αij≤1。同时，假设各子系统对其他子系统的竞争合作系数相同，即αi1=αi2=···=αij，表示港口子系统i对其他子系统的合作竞争态度一致。

假设5：港口群系统的演化在政府的宏观调控之下，且政府干预系数-1≤Gi≤1。政府干预系数反映了政府对港口发展的支持或抑制程度。

1.3 模型构建。港口群系统演化模型以logistic 阻滞增长模型为基础，引入竞争合作系数和政府干预系数，考虑多个子系统在相互竞争合作和政府干预的情况下序参量的演化趋势和结果；选取港口群系统中各子系统的盈利能力xi为序参量，来描述港口群系统的自组织与他组织复合协同演化过程，得到港口群系统协同演化模型：

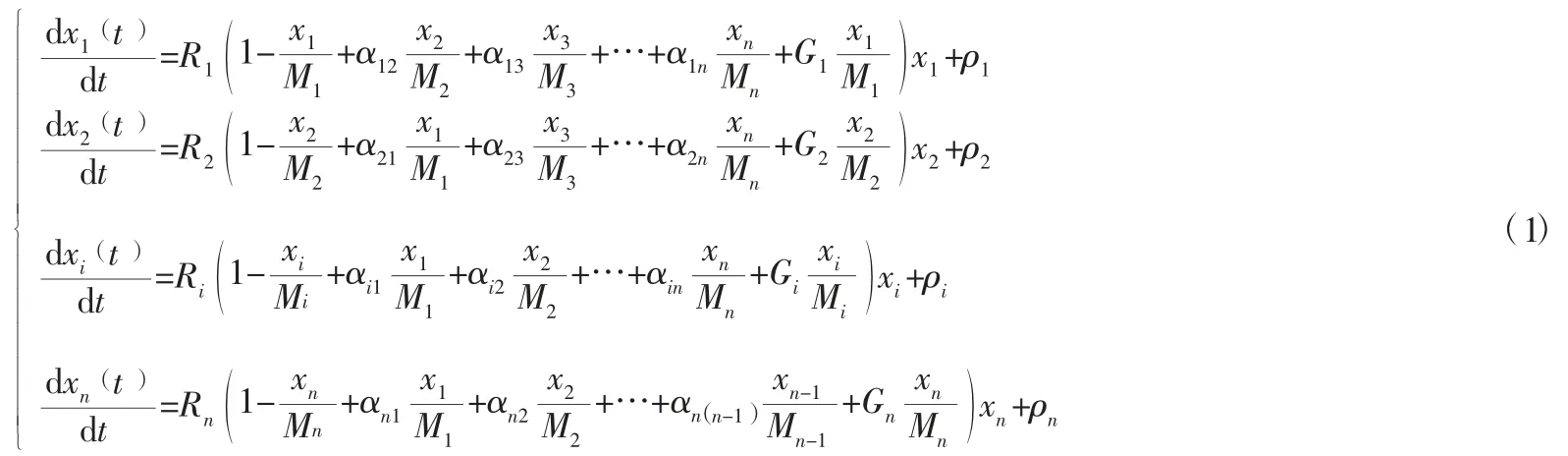
本文以津冀港口群系统为基础，综合考虑天津港、秦皇岛港、唐山港、黄骅港四个港口子系统之间的协同演化过程，即考虑n=4 时，四个港口子系统的港口群系统协同演化。

2 模型的稳定性分析

2.1 两个子系统模型的稳定性分析。当港口群系统中只有两个港口子系统时，即式（1） 中n=2 时模型旨在得到两个港口子系统的序参量x1,x2的演化趋势，不需要对方程进行求解，只需求出模型的平衡点并进行稳定性分析，设二阶非线性自治微分方程的平衡点为当xi从Ai点的某一稳定邻域内的任一初值出发时，都可以使得则称Ai是微分方程的平衡点。因此可以得到四个平衡点

针对非线性微分方程，可以依据近似线性方程判断方法来判定其平衡点的稳定性，在平衡点Ai对f（x1,x2）和g（x1,x2）进行泰勒展开，只需要保留一次项，可以得到两个子系统时的演化模型的近似线性方程组：

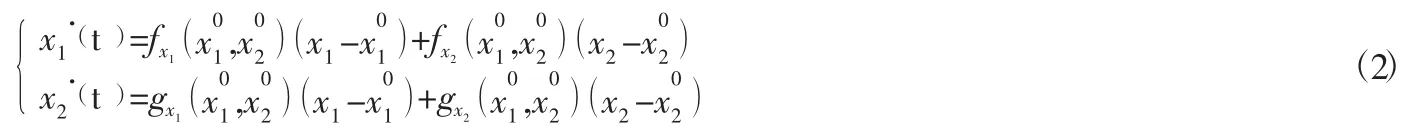
其近似线性方程组（2） 的系数矩阵记为：

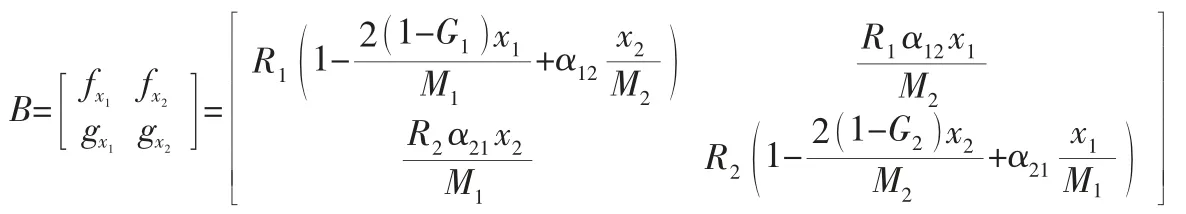
应用动态系统的系数矩阵及判别指标方法对平衡点的稳定性进行分析，可得A1是不稳定点，A2、A3有一个主体序参量为0，即有一个子系统被系统淘汰；A4点稳定的前提是x1、x2＞0，故当1-G1+α21＞0，1-G2+α12＞0 且（1-G2）（1-G1）-α21α12＞0 时A4局部稳定，可得A4是渐近稳定点。

2.2 三个及以上子系统模型的稳定性分析。当港口群系统中有i（i≥ 3 ）个子系统时，设dx/dt=f（x），其中：

当f（0）=0，即dx/dt=0 时，且在某域G:||x||≤A（A为常数） 内存在连续的偏导数，因而方程组dx/dt=f（x）由初始条件x（t0）=x0所确定的解在原点的某个邻域内存在且唯一，x=0 是其特殊解。

3 津冀港口群系统演化仿真分析

3.1 变量说明。考虑到模型中各变量与津冀各港口实际数据的关联性，本文以津冀港口群系统的发展现状和相关数据为基础，对模型中的变量进行量化分析：

（1） 其中子系统i的盈利能力xi是系统的序参量，决定着各子系统演化的方向和兴衰。对于港口子系统而言，吞吐量越大证明港口子系统的盈利能力越强，假设港口吞吐量为Ti，则子系统i的盈利能力xi≈Ti。

（2） 子系统i初始盈利能力xi0近似等于系统演化起点的吞吐量Ti0。

（3） 在一定的时间和相对稳定的空间内，子系统i的盈利能力的固有增长率Ri不变。假设子系统i演化至新的稳定状态的时间为ti，初始盈利能力为xi0，一段时间内的平均盈利能力为，则固有增长率

（4） 港口的吞吐能力除了受到自身条件的限制，还受到腹地市场需求的影响，当市场需求大于港口吞吐能力时，港口处于饱和状态，最大盈利能力近似等于港口吞吐能力；当市场需求小于港口吞吐能力时，最大盈利能力近似等于市场需求。设港口i的吞吐能力为Ci，市场需求为Di，则有

（5） 港口子系统之间的竞争合作系数主要体现在各子系统之间的竞争合作对系统演化的贡献或阻碍上。本文设定竞争合作系数的取值范围是［-1,1 ］，当αij=0 时，表示在系统内部各子系统间不存在合作竞争，依靠自身条件独立发展；当αij＞0 时，表示各子系统间的竞争合作对系统演化的促进作用；当αij＜0 时，表示各子系统间的竞争合作对系统演化的阻碍作用。

（6） 津冀港口群系统是典型的政府主导型港口群，政府对港口建设规模、业务类型、发展方向和战略等方面有着引导和决策的作用，对津冀港口群系统而言，政府政策的干预是最重要的外部他组织作用。

3.2 数据来源及处理。根据中国港口网数据得知，津冀港口群四个港口的年设计通过能力分别为天津港3.82 亿吨，秦皇岛港2.37 亿吨，唐山港4.22 亿吨，黄骅港1.82 亿吨。各港口吞吐量及增长率如表1 所示。

表1 2009～2015 年各港口吞吐量及增长率

根据以上对变量的假设和说明，得到模型中相关变量的数据如表2 所示。

表2 津冀港口群系统协同演化模型数据

3.3 津冀港口群系统自组织演化仿真分析。利用Matlab 工具仿真，分析系统内部的自组织作用，即相互作用系数αij对系统序参量xi演化趋势的影响。理想状态下，假设各子系统都是独立发展的，即各子系统之间的竞争合作系数αij=0，得到各子系统独立发展时盈利能力xi的演化趋势，如图1 所示。由图1 可知，当各子系统间没有相互作用独立发展时，（1） 各子系统的盈利能力xi受最大盈利能力的限制，演化至稳定状态时的盈利能力无限趋近于子系统独立发展的最大盈利能力Mi。（2） 由于初始盈利能力是演化过程基期各子系统相互作用下的值，受最大盈利能力的约束，天津港、唐山港和秦皇岛港演化过程前期曲线有明显的下降过程，由于黄骅港的初始盈利能力小于最大盈利能力，且固有增长率R4为正，经过一段时间的演化，增长至M4后进入稳定状态。

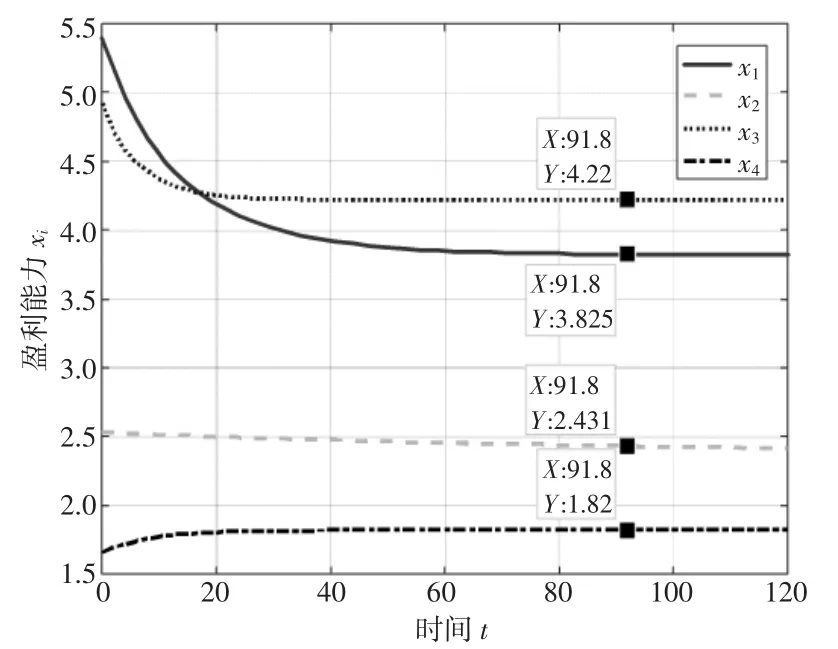
图1 αij=0 时xi 的演化趋势

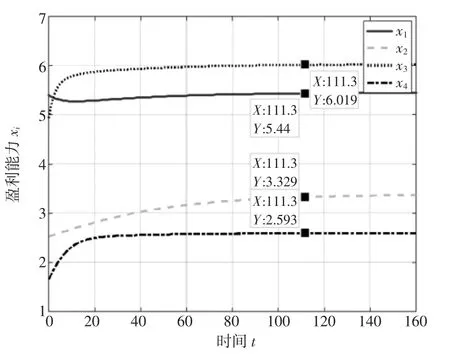
图2 αij=0.1 时xi 的演化趋势

当各子系统间的竞争合作系数αij＞0 时，为分析竞争合作系数αij的变化对各子系统演化趋势的影响，令竞争合作系数都为正且相等，取αij=0.1，得到各子系统的演化趋势如图2 所示；再分别取α11=α12=α13=0.1，α21=α23=α24=0.5，α31=α32=α34=0.3，α41=α42=α43=0.2，演化趋势如图3 所示。对比图2 和图6 可知，当αij＞0 时，（1） 竞争合作系数越大，演化至稳定状态时的盈利能力越大。（2） 在竞争合作系数的作用下，秦皇岛港的盈利能力逐渐超过了天津港的吞吐能力，说明合理的竞争合作策略，能够极大地弥补独立发展时最大盈利能力对自身的限制。

图3 αij＞0 且不相等时xi 的演化趋势

图4 αij=-0.1 时xi 的演化趋势

当各子系统间的竞争合作系数αij＜0 时，为分析竞争合作系数αij的变化对各子系统演化趋势的影响，令竞争合作系数都为负且相等，取αij=-0.1，得到各子系统的演化趋势如图4 所示，再分别取α11=α12=α13=-0.15，α21=α23=α24=-0.1，α31=α32=α34=-0.3，α41=α42=α43=-0.05，演化趋势如图5 所示；保持其他子系统的竞争合作系数αij＜0 且不变，以唐山港为例，逐渐增大竞争合作系数的绝对值，观察其演化趋势的变化，当取唐山港的竞争合作系数α3j=-0.4 时，演化趋势如图6 所示。对比图4 和图8 可知，当αij＜0 时，（1） 竞争合作系数的绝对值越大，即各子系统采取的竞争合作策略对其演化的阻碍程度越高时，演化至稳定状态时的盈利能力越小。（2） 在竞争合作系数的阻碍作用下，秦皇岛港和黄骅港的盈利能力逐渐超过了唐山港的盈利能力，说明不合理的恶意竞争策略，会导致港口盈利能力的急剧下降，虽然在独立发展条件下，唐山港的最大盈利能力是四个港口中最大的，但是由于不合理的竞争合作策略导致的阻碍作用，使其稳定状态下的盈利能力被其他港口反超，且严重影响了其他三个港口的盈利能力的提升，从而阻碍了整个港口群系统的协同发展。对比图5 和图9 可知，当αij＜0 且绝对值不断增大突破某一临界点时，唐山港的盈利能力趋近于0。由此可得，当αij＜0 且绝对值不断增大至突破某个临界点，即当竞争合作系数对子系统的阻碍达到一定程度时，会导致该子系统的盈利能力无限趋近于0，即子系统被整个系统淘汰。

图5 αij＜0 且不相等时xi 的演化趋势

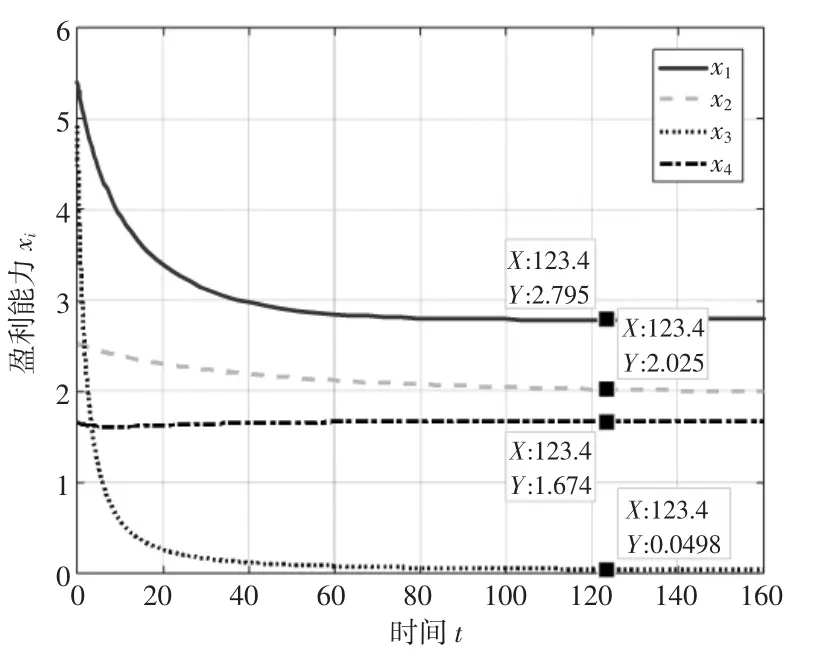
图6 αij＜0 且α3j=-0.4 时xi 的演化趋势

3.4 政府干预下系统自组织与他组织复合演化仿真分析。本节研究政府的干预程度对演化趋势的影响。假设各港口子系统独立发展且由当地政府单独管理，即αij=0，且政府间无关联。在Gi的取值范围内分别取G1=0.5，G2=0.2，G3=-0.15，G4=-0.3，得到xi的演化趋势如图7 所示。由图7 可知，（1） 各港口子系统在独立发展且由当地政府单独管理的情况下，达到新的稳定状态时的盈利能力主要受到港口最大盈利能力的限制和政府干预的影响；（2） 对比图7 和图1，由x1和x2的变化可知，各港口独立发展时，政府的正向干预能够促使系统突破自身发展的限制，使稳定状态时的盈利能力xi ＞Mi；（3） 由x3和x4的变化可知，政府的负向干预会约束子系统盈利能力的增长，使稳定状态时的盈利能力xi＜Mi。

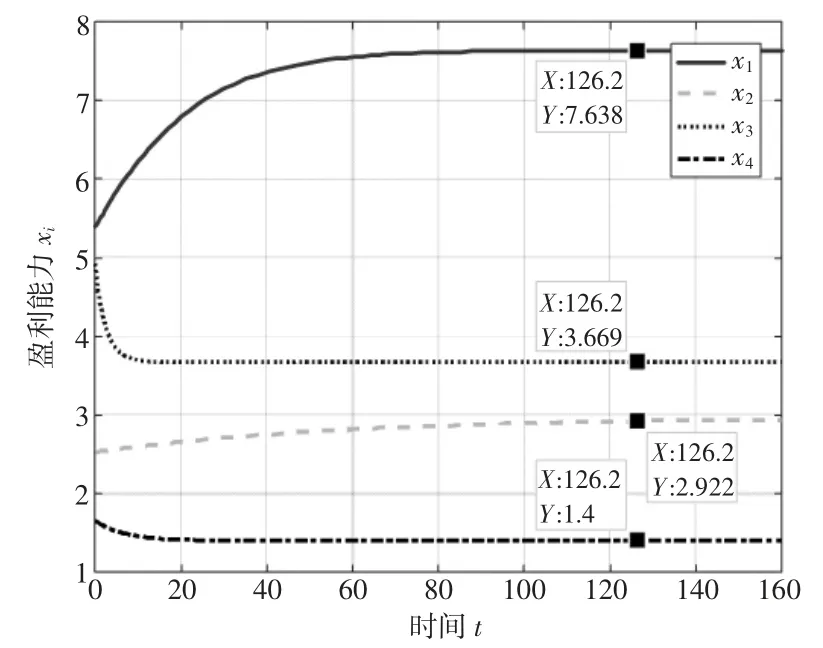
图7 αij=0 且Gi 不相等时xi 的演化趋势

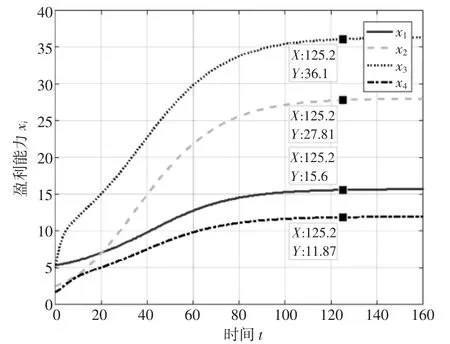
图8 αij＞0 且Gi=0.1 时xi 的演化趋势

当各子系统之间的竞争合作系数αij＞0 且政府干预系数Gi＞0 时，为得到政府干预系数对系统盈利能力演化趋势的影响，取α11=α12=α13=0.1，α21=α23=α24=0.5，α31=α32=α34=0.3，α41=α42=α43=0.2，且保持不变，分别取G1=0.08，G2=0.15，G3=0.2，G4=0.3。得到盈利能力xi的演化趋势如图8 和图9 所示。对比图8 和图9 可知，当αij保持不变且Gi＞0 时，（1） 政府干预系数越大，即政府干预对港口群系统的演化起到明显的促进作用时，演化至稳定状态的盈利能力越大；（2） 由天津港和黄骅港的变化可知，在政府的正向干预下，由于黄骅港的干预程度高于天津港，演化至稳定状态，黄骅港的盈利能力超过了天津港。

图9 αij＞0, Gi＞0 且不相等时xi 的演化趋势

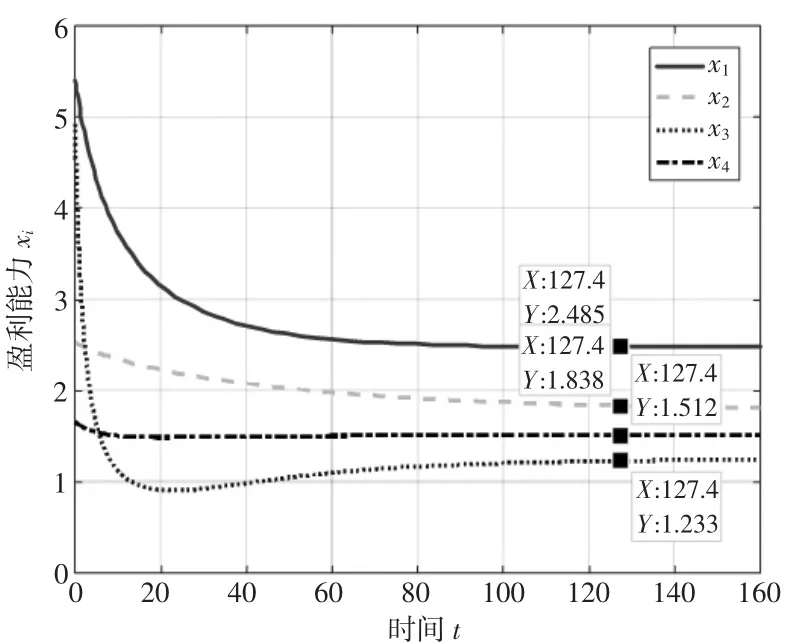
图10 αij＜0 且Gi=-0.1 时xi 的演化趋势

当各子系统之间的竞争合作系数αij＜0 且政府干预系数Gi＜0 时，为得到政府负向干预时Gi的变化对演化趋势的影响，分别取α11=α12=α13=-0.15，α21=α23=α24=-0.1，α31=α32=α34=-0.3，α41=α42=α43=-0.05，且保持不变，首先取Gi=-0.1，得到盈利能力xi的演化趋势如图10 所示；再分别取G1=-0.1，G2=-0.15，G3=-0.2，G4=-0.3，得到盈利能力xi的演化趋势如图11 所示。以唐山港为例，逐渐增大政府干预系数的绝对值，即增大政府的负向干预，观察其演化趋势的变化，当唐山港的政府干预系数G3=-0.9 时，得到盈利能力x3的演化趋势如图12 所示。对比图3 和图10 可知，当竞争合作系数αij＜0 且不变时，政府的负向干预会放大各子系统间的相互阻碍作用，降低各子系统的盈利能力，且政府的负向干预越大，对子系统间的相互作用的放大作用越明显。对比图10 和图11 可知，当αij保持不变且Gi＜0 时，（1） 政府干预系数的绝对值越大，即政府干预对港口群系统的演化起抑制或阻碍作用越大时，演化至稳定状态的盈利能力越小；（2） 在天津港的政府干预系数不变的前提下，由于αij＜0，各港口处于竞争状态，另外三个港口的盈利能力在政府的负向干预增强的情况下盈利能力降低，天津港在政府的干预下在竞争中胜出，盈利能力提高。对比图11 和图12 可知，保持其他港口的政府干预系数不变，逐渐增大唐山港的政府干预系数的绝对值，即增大政府对唐山港的负向干预，盈利能力降低，当唐山港的政府干预系数G3超过某一阈值时，在稳定状态时被黄骅港超越。

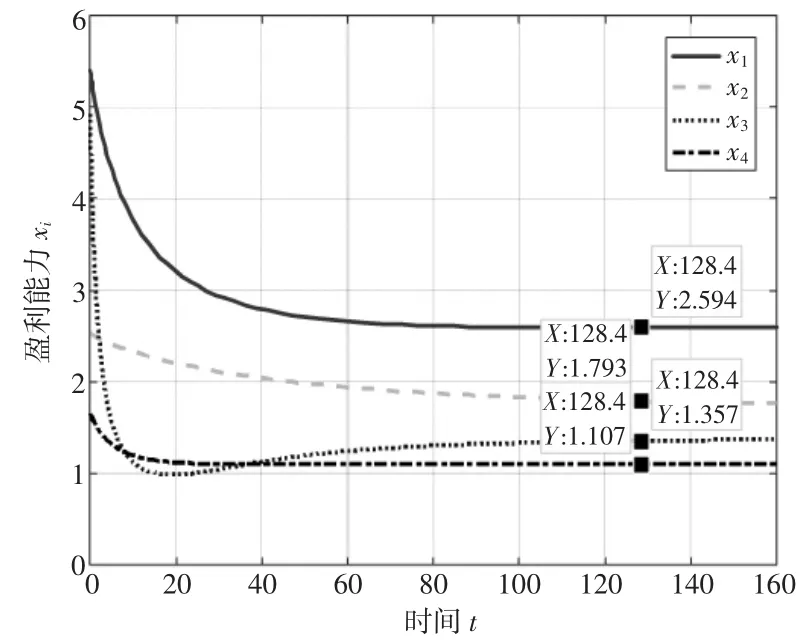
图11 αij＜0, Gi＜0 且不相等时xi 的演化趋势

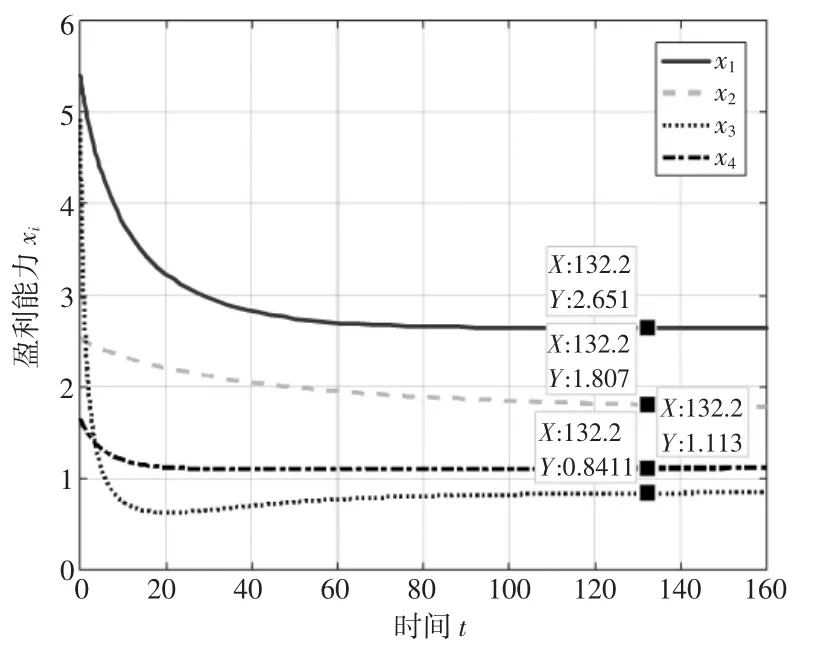
图12 αij＜0, G3=-0.9 时xi 的演化趋势

4 结束语

本文以自组织理论为基础，构建了以logistic 模型为基础的协同演化模型。选取港口的盈利能力为序参量，综合考虑初始盈利能力、竞争合作系数、独立最大盈利能力和政府干预系数等因素的影响下，对津冀港口群系统的演化趋势进行仿真分析。通过分析得出：津冀港口群系统的演化与各子系统的独立最大盈利能力、竞争合作系数、政府干预系数密切相关。各港口在充分发挥港口群系统自组织作用的前提下，应重视他组织作用对系统演化的影响，充分发挥政府的他组织作用，协同制定各项方针政策，通过系统内各主体间的合作效应与政府的正向干预，推动港口群系统向有利的方向演化。