基于系统动力学的药品第三方物流库存管理仿真研究
周浩然,李 钊,马志强 (江苏大学 管理学院,江苏 镇江212013)
0 引 言
供应商管理库存(VMI) 是在供需双方签订协议前提下,供应商负责库存管理,目的是使双方的成本尽量降到最低。而第三方物流管理库存(TMI) 是供应商管理库存的改进版,药品供应链中,第三方物流的位置比较特殊,主要起到的是协调作用,能使供需双方取消各自的独立库存,不仅提供基础的物流服务,还提供更为精准的药品需求预测,使药品供应链更加协调、经济与高效[1]。我国在《药品安全“十二五”规划》中明确提出,要推动第三方药品物流发展。然而,在药品集中采购的大环境下,大多数医药企业仍使用自营物流承担药品的运输、仓储等任务,存在着库存管理专业程度化低[2]、市场集中度低[3]、发展水平低[4]等问题。
1 文献综述与问题提出
近年来,随着第三方物流的崛起,作为新型物流模式,国内外学者开始重视其在医药物流领域的应用。Chuanzhe 等[5](2017) 提出第三方药品冷链物流系统模型。Singh R K 等[6](2018) 则用AHP 与TOPSIS 方法研究了第三方医药冷链物流。国内第三方医药物流研究才刚开始起步,目前主要研究集中于第三方医药物流的可行性研究[7]与现代医药物流发展建议[8]等。
以上研究成果对第三方物流参与管理药品库存打下了良好基础,但仍有以下两点问题:(1) 基于第三方物流研究库存大多为定性研究,不够深入与具体;(2) 站在第三方物流角度考虑药品库存管理的研究较少。因此,本研究分析了基于第三方物流对医院药品库存的影响因素,利用系统动力学,将定性问题转化定量问题分析,结论以期为医院药品库存管理引入TMI 提供参考与决策依据。
2 模型构建
2.1 药品第三方物流库存管理运作模式
如图1 所示,在TMI 运作模式下,药品供应商与医院将库存委托给第三方物流进行管理,即供应链发货补货由第三方物流进行管理。当供应商完成药品订单后,储存在自己的仓库,由TPL进行管理,同时TPL为及时满足医院的需求,在医院附近设立有配送中心,以便满足医院的需求。供应链上信息能够及时共享,医院的需求信息与供应商、TPL共享;TPL的库存信息与供应商共享;供应商的生产信息与TPL共享。
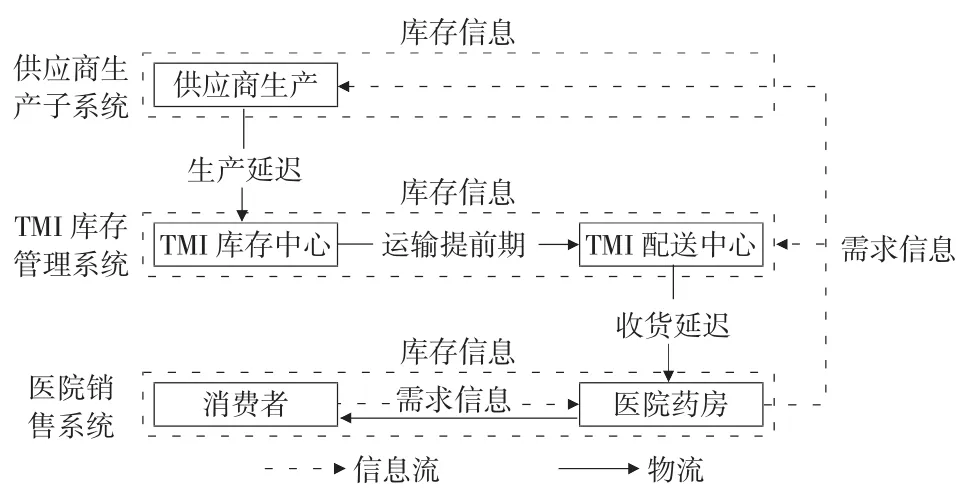
图1 TMI 运作模式
2.2 相关参数与变量
状态变量:在制品库存(WIP)、供应商库存(VINV)、TPL库存(TPLW)、TPL在途库存(GIT)、配送中心库存(TPL-DC)、医院药品库存(SI)。
速率变量:配送中心收货率(SAT)、药品交单率(ORT)、药品到库率(CRT)、配送中心配送率(DCDR)、TPL补货率(RPT)、TPL发货率(SPT)、医院出库率(HOR)。
辅助变量:系统库存水平(SINV)、目标系统库存水平(TINV)、配送中心库存水平(DC-INV)、TPL补货量(ROT)、TPL再补货点(W-ROP)、TPL库存水平(TPL-INV)、发货策略(SOT)、再发货点(D-ROP)、供应商需求率(VCON)、医院计划入库量(HPS)、医院期望库存水平(EIL)、医院预测日需求(ASR)、药品短缺提示(W)。
常量:延迟时间(DT)、安全库存天数(Tη、Tε)、需求预测平滑系数(SC)。
由运作模式构建的系统动力学模型如图2 所示。

图2 药品第三方物流库存管理流程图
3 实验分析
3.1 仿真分析
本研究将调研的两家医院数据作为实证数据,假设两家医院的药品联合由第三方物流管理库存,不失一般性,以药品“注射用青霉素钠”的进销存数据为例,对药品第三方物流库存管理模型进行分析。相关初始数据见表1。
模型假设:
(1) 医院将需求信息、库存信息向供应链上游实时分享,与第三方物流共同确定客户需求量;
(2) 生产商所提供药品优良率为100%,不存在医院退货现象;
(3) 各环节的补货、发货均受到物流操作与运输延迟的制约;
(4) 医院可随时向配送中心发出订单。
根据调研数据,医院1 药品销售最大值Max=80,最小值Min=0,平均数且符合正态分布ε~N(14.85,10.512),因此,在模型中医院1 药品的日需求量的数学方程可以设置为:
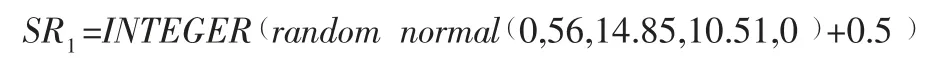
同理,医院2 药品销售最大值Max=61,最小值Min=0,平均数且符合正态分布ε~N(18.72,11.152),模型中医院2 药品日需求量的数学方程式为:

在上述初始条件下对模型进行仿真分析,初始条件下仿真的系统表现如图3 至图7 所示。

表1 模型相关初始数据

图3 两家医院日需求量及总需求

图4 系统库存水平

图5 医院药品库存及库存总量

图6 药品缺药监控
图3 反映的是医院药品的日需求量,为更直观分析模型,临时构造了辅助变量SR,为两家医院药品日需求之和。从图3 中可以看出,药品日总需求量变化仍然符合正态分布,证明了两个正态分布之和还是正态分布,药品日总需求的平均值为37 件。
本研究构建了系统库存水平(SIN)V,目的是能更直观地看到引入第三方物流后整个药品供应链的运作状况,如图4 所示,其值是TPL库存水平与供应商库存水平之和,从图4 中我们可以得到初始状态下系统库存水平的平均值为2 044 件。
两家医院的药品库存量及总量如图5 所示,为了更好对模型进行分析,临时构建辅助变量SI,为两家医院药品库存的总和。图5 中反映了医院药品库存水平的变化,从库存曲线变化来看,医院药品库存水平较为理想,总库存水平平均为214 件,相比两家医院的总需求量37 件,约为5.8 天的库存准备,是较理想的库存水平。
与此同时,两家医院的药品缺药情况如图6 所示。可以看到医院缺药监控被压在0 以下,无缺货。原因是在第三方物流管理下,配送中心通过每天对药品日需求量的预测,对医院仓库进行补货,医院药品库存需要保留一定的安全库存,保证在配送中心到货之前不会缺货。当药品日需求量小于医院药品库存时,则药品出库率等于药品日需求,当药品日需求大于医院药品库存时,第三方物流就会通过设立在医院附近的配送中心立即对医院进行发货,所以只要配送中心库存有足够的库存量,就不会发生药品缺货现象。配送中心平均库存约为78 件,能满足医院2.1 天需求,如图7 所示。

图7 配送中心库存量
3.2 敏感性分析
通过敏感分析找到敏感性参数或变量,通过改变相应参数或变量对模型进行优化。
(1) 改变安全库存系数
在初始条件下模型没有出现缺货现象,而医院药品库存水平与缺药情况关系密切,说明医院库存水平还较高,有降低的可能性,将两家医院的安全库存系数都调整到5 天,得到的仿真结果如图8、图9 所示。

图8 医院1 缺药与库存关系

图9 医院2 缺药与库存关系
从图8、图9 中可以看出,当医院1 安全库存系数为5 时出现了两次缺药,因为安全库存系数降低导致药品库存降低,出现了低于药品日需求量的情况,从而缺货。而医院2 仍然没有缺药情况出现。经过不断调试,将医院1 安全库存系数设置为6,医院2 安全库存系数设置为4 时是最优设置,此时医院药品总库存平均为124 件,相较与初始条件下的214 件下降了90 件,且无缺货现象出现。?(2) 改变库存偏差率调整时间(Tα、Tγ)与供应商需求调整时间(Tμ)。通过敏感性分析发现,增加库存偏差调整时间会使库存调整的时间也越来越长,库存波动的振幅与频率也越来越大。因此在设置库存调整周期时要根据两家医院自身的药品销售状况,根据实际情况来选择合理的库存调整时间。一般销售比较稳定的药品可以选择较长的库存调整时间,方便药品的库存管理,反之就要选择采购频率更高的策略,制定较短的库存调整时间。
(3) 对延迟时间DT1、DT2以及DT3进行不同赋值发现,增加延迟时间后,医院药品库存在一段时间后消耗会增加,最后会恢复正常,原因是在增加延迟时间后,医院的订单会累积,开始会消耗原本的库存,导致医院库存量降低,达到平衡后的医院药品库存量只有小幅度的波动。
(4) 通过敏感性分析不断调试模型,得到本模型的最优设置参数为:Tα=13、Tγ=3、Tβ=3、Tμ=4、Tη=6,Tε=4。针对这组优化过后的参数进行仿真实验,得到了一个较好的药品TMI 系统动力学模型,结果如图10、图11 所示。

图10 改进后的系统库存水平曲线

图11 改进后的医院药品库存曲线
由图10、图11 可以看出,改进后的系统动力学模型与初始模型相比,系统库存水平由原来的2 044 件降至1 153 件,两家医院总药品库存平均水平由原来的214 件降至124 件,没有出现缺药现象,药品供应链效率整体上有了大幅提升,本模型通过行为再现测试,因此图中所示都与现实情况符合,该模型能有效模拟第三方物流参与管理药品供应链的现实情况。改进后的药品缺药率如图12 所示:
4 结论与展望
本研究在传统药品供应链中引入第三方物流,构建基于第三方物流的药品库存管理系统动力学模型,研究药品TMI 模式的系统表现,并通过敏感性分析对模型进行优化。结果显示,第三方物流能够降低药品供应商与医院的药品库存波动,并显著降低系统库存水平和医院药品库存,信息共享机制能实现即时配送,减少药品缺药率。实施药品TMI 模式有着良好的成效,但此模式实施却不尽人意,还存在着许多问题,如第三方物流认证缺失、行业标准不规范、监督机制不完善等。面对诸多问题,我国应尽快建立和完善与新版GSP 配套的相关法律法规;改变传统观念,让药品供应链成员形成合作意识;第三方物流要提升自己物流服务能力等。总之,我国第三方医药物流虽才刚起步,目前还处于试点阶段,但随着医药卫生体制改革的推进,第三方药品物流将有着大好的发展机遇。

图12 改进后的药品缺药率

